2.E: Linear Functions(Exercises)
- Page ID
- 19660
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)2.1 Linear Functions
Verbal
1) Terry is skiing down a steep hill. Terry's elevation, \(E(t)\), in feet after \(t\) seconds is given by \(E(t)=3000−70t\). Write a complete sentence describing Terry’s starting elevation and how it is changing over time.
- Answer
-
Terry starts at an elevation of \(3000\) feet and descends \(70\) feet per second.
2) Maria is climbing a mountain. Maria's elevation, \(E(t)\), in feet after \(t\) minutes is given by \(E(t)=1200+40t\). Write a complete sentence describing Maria’s starting elevation and how it is changing over time.
3) Jessica is walking home from a friend’s house. After \(2\) minutes she is \(1.4\) miles from home. Twelve minutes after leaving, she is \(0.9\) miles from home. What is her rate in miles per hour?
- Answer
-
\(3\) miles per hour
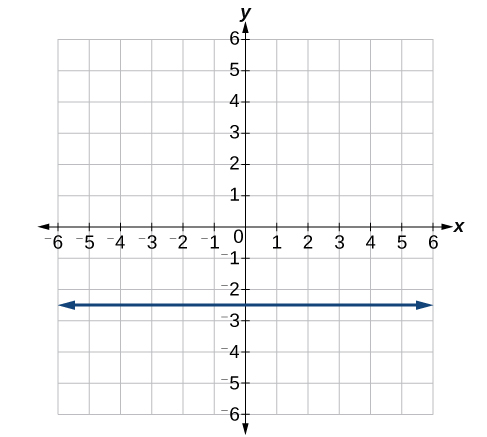
4) Sonya is currently \(10\) miles from home and is walking farther away at \(2\) miles per hour. Write an equation for her distance from home \(t\) hours from now.
5) A boat is \(100\) miles away from the marina, sailing directly toward it at \(10\) miles per hour. Write an equation for the distance of the boat from the marina after \(t\) hours.
- Answer
-
\(d(t) =100−10t\)
6) Timmy goes to the fair with \(\$40\). Each ride costs \(\$2\). How much money will he have left after riding \(n\) rides?
Algebraic
For the exercises 7-14, determine whether the equation of the curve can be written as a linear function.
7) \(y= \dfrac{1}{4}x+6\)
- Answer
-
Yes
8) \(y=3x−5\)
9) \(y=3 x^2 −2\)
- Answer
-
No
10) \(3x+5y=15\)
11) \(3 x^2 +5y=15\)
- Answer
-
No
12) \(3x+5 y^ 2 =15\)
13) \(−2 x^2 +3y^2 =6\)
- Answer
-
No
14) \(−\dfrac{x−3}{5} =2y\)
For the exercises 15-24, determine whether each function is increasing or decreasing.
15) \(f(x)=4x+3\)
- Answer
-
Increasing
16) \(g(x)=5x+6\)
17) \(a(x)=5−2x\)
- Answer
-
Decreasing
18) \(b(x)=8−3x\)
19) \(h(x)=−2x+4\)
- Answer
-
Decreasing
20) \(k(x)=−4x+1\)
21) \(j(x)=\dfrac{1}{2}x−3\)
- Answer
-
Increasing
22) \(p(x)=\dfrac{1}{4}x−5\)
23) \(n(x)=−\dfrac{1}{3}x−2\)
- Answer
-
Decreasing
24) \(m(x)=−\dfrac{3}{8}x+3\)
For the exercises 25-29, find the slope of the line that passes through the two given points.
25) \((2, 4)\) and \((4, 10)\)
- Answer
-
\(3\)
26) \((1, 5)\) and \((4, 11)\)
27) \((−1,4)\) and \((5,2)\)
- Answer
-
\(–\dfrac{1}{3}\)
28) \((8,−2)\) and \((4,6)\)
29) (6, 11) and (−4, 3)
- Answer
-
\(\dfrac{4}{5}\)
For the exercises 30-37, given each set of information, find a linear equation satisfying the conditions, if possible.
30) \(f(−5)=−4\), and \(f(5)=2\)
31) \(f(−1)=4\) and \(f(5)=1\)
- Answer
-
\(f(x)=−\dfrac{1}{2}x+\dfrac{7}{2}\)
32) \((2,4)\) and \((4,10)\)
33) Passes through \((1,5)\) and \((4,11)\)
- Answer
-
\(y=2x+3\)
34) Passes through \((−1, 4)\) and \((5, 2)\)
35) Passes through \((−2, 8)\) and \((4, 6)\)
- Answer
-
\(y=−\dfrac{1}{3}x+\dfrac{22}{3}\)
36) \(x\) intercept at (−2, 0) and \(y\) intercept at (0,−3)
37) \(x\) intercept at (−5, 0) and \(y\) intercept at (0, 4)
- Answer
-
\(y=\dfrac{4}{5}x+4\)
Graphical
For the exercises 38-,40 find the slope of the lines graphed.
38)
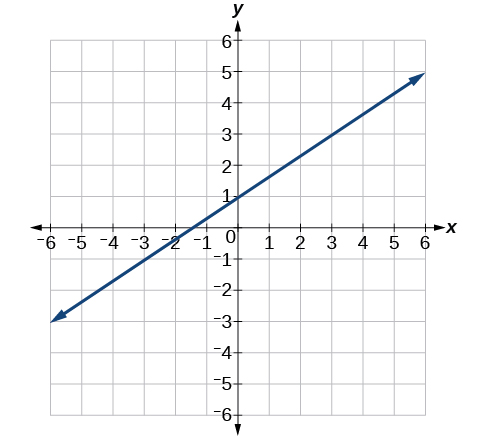
39)
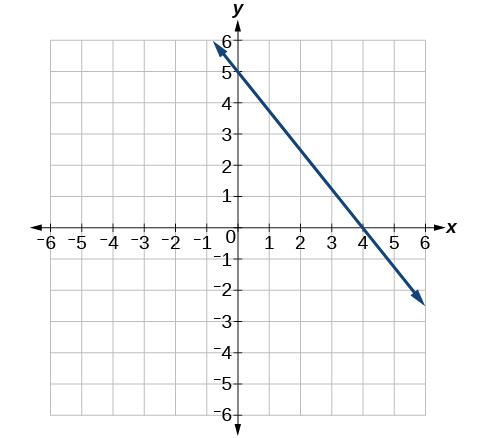
- Answer
-
\(−\dfrac{5}{4}\)
40)
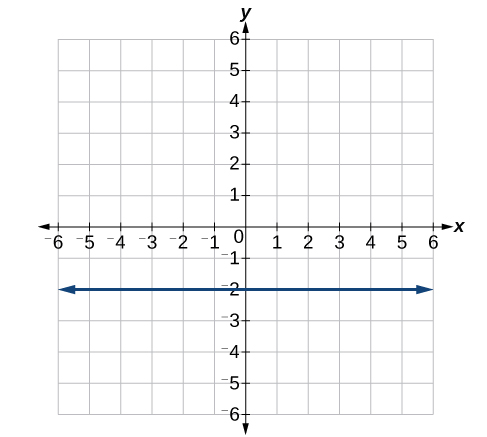
For the exercises 41-46, write an equation for the lines graphed.
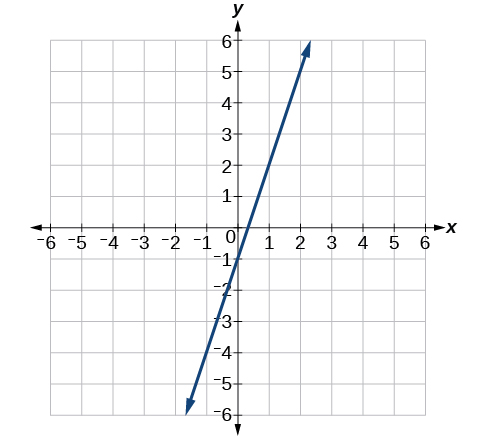
41)
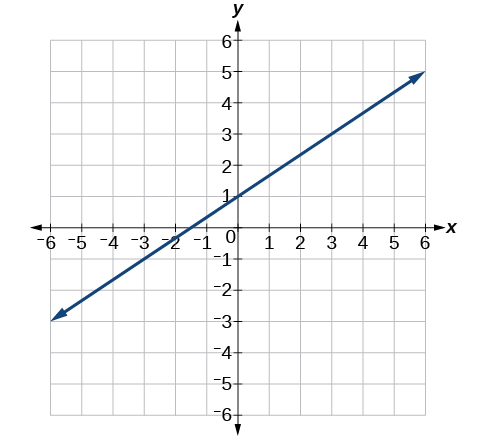
- Answer
-
\(y= \dfrac{2}{3} x+1\)
42)
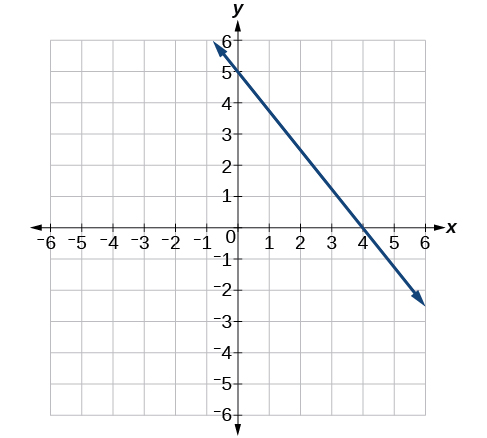
43)
- Answer
-
\(y=−2x+3\)
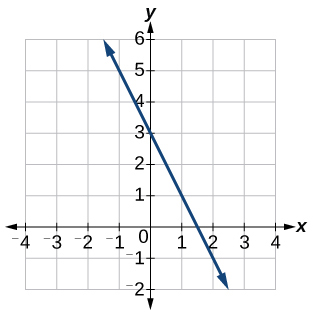
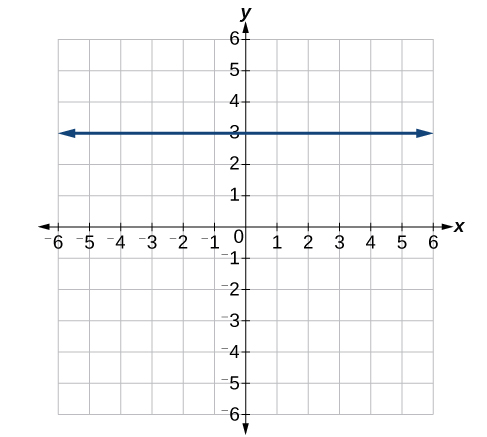
44)
45)
- Answer
-
\(y=3\)
46)
Numeric
For the exercises 47-51, which of the tables could represent a linear function? For each that could be linear, find a linear equation that models the data.
47)
| \(x\) | 0 | 5 | 10 | 15 |
|---|---|---|---|---|
| \(g(x)\) | 5 | –10 | –25 | –40 |
- Answer
-
Linear, \(g(x)=−3x+5\)
48)
| \(x\) | 0 | 5 | 10 | 15 |
|---|---|---|---|---|
| \(h(x)\) | 5 | 30 | 105 | 230 |
| \(x\) | 0 | 5 | 10 | 15 |
|---|---|---|---|---|
| \(f(x)\) | –5 | 20 | 45 | 70 |
- Answer
-
Linear, \(f(x)=5x−5\)
49)
| \(x\) | 5 | 10 | 20 | 25 |
|---|---|---|---|---|
| \(k(x)\) | 28 | 13 | 58 | 73 |
| \(x\) | 0 | 2 | 4 | 6 |
|---|---|---|---|---|
| \(g(x)\) | 6 | –19 | –44 | –69 |
- Answer
-
Linear, \(g(x)=−\dfrac{25}{2}x+6\)
50)
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | –4 | 16 | 36 | 56 |
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | –4 | 16 | 36 | 56 |
- Answer
-
Linear, \(f(x)=10x−24\)
51)
| \(x\) | 0 | 2 | 6 | 8 |
|---|---|---|---|---|
| \(k(x)\) | 6 | 31 | 106 | 231 |
Technology
52) If \(f\) is a linear function,\(f(0.1)=11.5\), and \(f(0.4)=–5.9\), find an equation for the function.
- Answer
-
\(f(x)=−58x+17.3\)
53) Graph the function \(f\) on a domain of \([ –10, 10 ]: f(x)=0.02x−0.01\). Enter the function in a graphing utility. For the viewing window, set the minimum value of \(x\) to be −10 and the maximum value of \(x\) to be 10.
54) Graph the function \(f\) on a domain of \([ –10, 10 ]:fx)=2,500x+4,000\)
- Answer
-
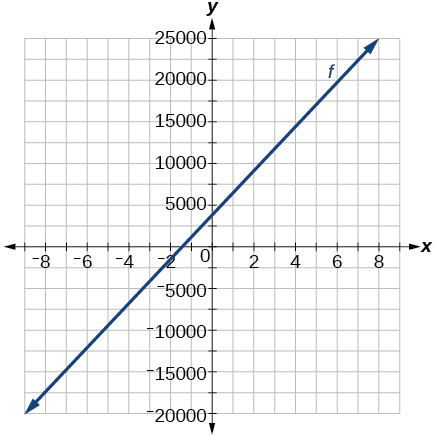
55) The Table below shows the input, \(w\), and output, \(k\), for a linear function \(k\).
- Fill in the missing values of the table.
- Write the linear function \(k\), round to \(3\) decimal places.
| \(w\) | –10 | 5.5 | 67.5 | b |
|---|---|---|---|---|
| \(k\) | 30 | –26 | a | –44 |
56) The Table below shows the input, \(p\), and output, \(q\), for a linear function \(q\).
- Fill in the missing values of the table.
- Write the linear function \(k\).
| \(p\) | 0.5 | 0.8 | 12 | b |
|---|---|---|---|---|
| \(q\) | 400 | 700 | a | 1,000,000 |
- Answer
-
- \(a=11\),900; \(b=1001.1\)
- \(q(p)=1000p−100\)
57) Graph the linear function \(f\) on a domain of \([ −10,10 ]\) for the function whose slope is \(\dfrac{1}{8}\) and y-intercept is \(\dfrac{31}{16}\). Label the points for the input values of \(−10\) and \(10\).
58) Graph the linear function \(f\) on a domain of \([ −0.1,0.1 ]\) for the function whose slope is \(75\) and \(y\)-intercept is \(-22.5\). Label the points for the input values of \(-0.1\) and \(0.1\).
- Answer
-
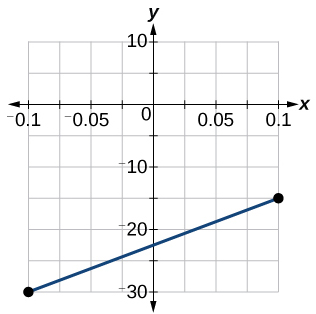
59) Graph the linear function \(f\) where \(f(x)=ax+b\) on the same set of axes on a domain of \([ −4,4 ]\) for the following values of \(a\) and \(b\).
- \(a=2;\) \(b=3\)
- \(a=2; \) \(b=4\)
- \(a=2;\) \(b=–4\)
- \(a=2;\) \(b=–5\)
Extensions
60) Find the value of \(x\) if a linear function goes through the following points and has the following slope: \((x,2),(−4,6),\) \(m=3\)
- Answer
-
\(x=−\dfrac{16}{3}\)
61) Find the value of \(y\) if a linear function goes through the following points and has the following slope: \((10,y),(25,100),\) \(m=−5\)
62) Find the equation of the line that passes through the following points: \((a, b)\) and \(( a, b+1 )\)
- Answer
-
\(x=a\)
63) Find the equation of the line that passes through the following points: \((2a, b)\) and (a, b+1)
64) Find the equation of the line that passes through the following points: \((a, 0)\) and \((c, d)\)
- Answer
-
\(y=\dfrac{d}{c−a}x−\dfrac{ad}{c−a}\)
Real-World Applications
65) At noon, a barista notices that she has \(\$20\) in her tip jar. If she makes an average of \(\$0.50\) from each customer, how much will she have in her tip jar if she serves \(n\) more customers during her shift?
66) A gym membership with two personal training sessions costs \(\$125\), while gym membership with five personal training sessions costs \(\$260\). What is cost per session?
- Answer
-
\(\$45\) per training session.
67) A clothing business finds there is a linear relationship between the number of shirts, \(n\), it can sell and the price, \(p\), it can charge per shirt. In particular, historical data shows that \(1,000\) shirts can be sold at a price of \(\$30\), while \(3,000\) shirts can be sold at a price of \(\$22\). Find a linear equation in the form \(p(n)=mn+b\) that gives the price \(p\) they can charge for \(n\) shirts.
68) A phone company charges for service according to the formula: \(C(n)=24+0\).1n, where \(n\) is the number of minutes talked, and \(C(n)\) is the monthly charge, in dollars. Find and interpret the rate of change and initial value.
- Answer
-
The rate of change is \(0.1\). For every additional minute talked, the monthly charge increases by \(\$0.1\) or \(10\) cents. The initial value is \(24\). When there are no minutes talked, initially the charge is \(\$24\).
69) A farmer finds there is a linear relationship between the number of bean stalks, \(n\), she plants and the yield, \(y\), each plant produces. When she plants \(30\) stalks, each plant yields \(30\) oz of beans. When she plants \(34\) stalks, each plant produces \(28\) oz of beans. Find a linear relationships in the form \(y=mn+b\) that gives the yield when \(n\) stalks are planted.
70) A city’s population in the year 1960 was \(287,500\). In 1989 the population was \(275,900\). Compute the rate of growth of the population and make a statement about the population rate of change in people per year.
- Answer
-
The slope is \(-400\). This means for every year between 1960 and 1989, the population dropped by \(400\) per year in the city.
71) A town’s population has been growing linearly. In 2003, the population was \(45,000\), and the population has been growing by \(1,700\) people each year. Write an equation, \(P(t)\), for the population \(t\) years after 2003.
72) Suppose that average annual income (in dollars) for the years 1990 through 1999 is given by the linear function: \(I(x)=1054x+23\),\(286,\) where \(x\) is the number of years after 1990. Which of the following interprets the slope in the context of the problem?
- As of 1990, average annual income was \(\$23,286\).
- In the ten-year period from 1990–1999, average annual income increased by a total of \(\$1,054\).
- Each year in the decade of the 1990s, average annual income increased by $1,054.
- Average annual income rose to a level of $23,286 by the end of 1999.
- Answer
-
c
73) When temperature is \(0\) degrees Celsius, the Fahrenheit temperature is \(32\). When the Celsius temperature is \(100\), the corresponding Fahrenheit temperature is \(212\). Express the Fahrenheit temperature as a linear function of \(C\), the Celsius temperature, \(F(C)\).
- Find the rate of change of Fahrenheit temperature for each unit change temperature of Celsius.
- Find and interpret \(F(28)\).
- Find and interpret \(F(–40)\).
2.2 Graphs of Linear Functions
Verbal
1) If the graphs of two linear functions are parallel, describe the relationship between the slopes and the \(y\)-intercepts.
- Answer
-
The slopes are equal; \(y\)-intercepts are not equal.
2) If the graphs of two linear functions are perpendicular, describe the relationship between the slopes and the \(y\)-intercepts.
3) If a horizontal line has the equation \(f(x)=a\) and a vertical line has the equation \(x=a\), what is the point of intersection? Explain why what you found is the point of intersection.
- Answer
-
The point of intersection is \((a,a)\). This is because for the horizontal line, all of the \(y\) coordinates are a and for the vertical line, all of the \(x\) coordinates are a. The point of intersection will have these two characteristics.
4) Explain how to find a line parallel to a linear function that passes through a given point.
5) Explain how to find a line perpendicular to a linear function that passes through a given point.
- Answer
-
First, find the slope of the linear function. Then take the negative reciprocal of the slope; this is the slope of the perpendicular line. Substitute the slope of the perpendicular line and the coordinate of the given point into the equation \(y=mx+b\) and solve for \(b\). Then write the equation of the line in the form \(y=mx+b\) by substituting in \(m\) and \(b\).
Algebraic
For the exercises 6-11, determine whether the lines given by the equations below are parallel, perpendicular, or neither parallel nor perpendicular:
6) \(4x−7y=10 \\ 7x+4y=1\)
7) \(3y+x=12 \\ −y=8x+1\)
- Answer
-
neither parallel or perpendicular
8) \(3y+4x=12 \\ −6y=8x+1\)
9) \(6x−9y=10 \\ 3x+2y=1\)
- Answer
-
perpendicular
10) \(y=\dfrac{2}{3}x+1 \\ 3x+2y=1\)
11) \(y=\dfrac{3}{4}x+1 \\ −3x+4y=1\)
- Answer
-
parallel
For the exercises 12-17, find the \(x\)- and \(y\)-intercepts of each equation
12) \(f(x)=−x+2\)
13) \(g(x)=2x+4\)
- Answer
-
\((–2, 0); (0, 4)\)
14) \(h(x)=3x−5\)
15) \(k(x)=−5x+1\)
- Answer
-
\(\left(\dfrac{1}{5}, 0\right); (0, 1)\)
16) \(−2x+5y=20\)
17) \(7x+2y=56\)
- Answer
-
\((8, 0); (0, 28)\)
For the exercises 18-23, use the descriptions of each pair of lines given below to find the slopes of Line 1 and Line 2. Is each pair of lines parallel, perpendicular, or neither?
18)
Line 1: Passes through \((0,6)\) and \((3,−24)\)
Line 2: Passes through \((−1,19)\) and \((8,−71)\)
19)
Line 1: Passes through \((−8,−55)\) and \((10, 89)\)
Line 2: Passes through \((9,−44)\) and \((4,−14)\)
- Answer
-
Line 1: \(m=8\) Line 2: \(m=–6\) Neither
20)
Line 1: Passes through \((2,3)\) and (4,−1)
Line 2: Passes through \((6,3)\) and \((8,5)\)
21)
Line 1: Passes through \((1,7)\) and \((5,5)\)
Line 2: Passes through \((−1,−3)\) and \((1,1)\)
- Answer
-
Line 1: \(m=–12\) Line 2: \(m=2\) Perpendicular
22)
Line 1: Passes through \((0,5)\) and \((3,3)\)
Line 2: Passes through \((1,−5)\) and \((3,−2)\)
23)
Line 1: Passes through \((2,5)\) and \((5,−1)\)
Line 2: Passes through \((−3,7)\) and \((3,−5)\)
- Answer
-
Line 1: \(m=–2\) Line 2: \(m=–2\) Parallel
24) Write an equation for a line parallel to \(f(x)=−5x−3\) and passing through the point \((2, –12)\).
25) Write an equation for a line parallel to \(g(x)=3x−1\) and passing through the point \((4,9)\).
- Answer
-
\(g(x)=3x−3\)
26) Write an equation for a line perpendicular to \(h(t)=−2t+4\) and passing through the point \((-4, –1)\).
27) Write an equation for a line perpendicular to \(p(t)=3t+4\) and passing through the point \((3,1)\).
- Answer
-
\(p(t)=−\dfrac{1}{3}t+2\)
28) Find the point at which the line \(f(x)=−2x−1\) intersects the line \(g(x)=−x\).
29) Find the point at which the line \(f(x)=2x+5\) intersects the line \(g(x)=−3x−5\).
- Answer
-
\((−2,1)\)
30) Use algebra to find the point at which the line \(f(x)= −\dfrac{4}{5}x +\dfrac{274}{25}\) intersects the line \(h(x)=\dfrac{9}{4}x + \dfrac{73}{10}\).
31) Use algebra to find the point at which the line \(f(x)=\dfrac{7}{4}x + \dfrac{457}{60}\) intersects the line \(g(x)=\dfrac{4}{3}x + \dfrac{31}{5}\).
- Answer
-
\(\left(−\dfrac{17}{5},\dfrac{5}{3}\right)\)
Graphical
For the exercises 32-37, match the given linear equation with its graph in the Figure below.
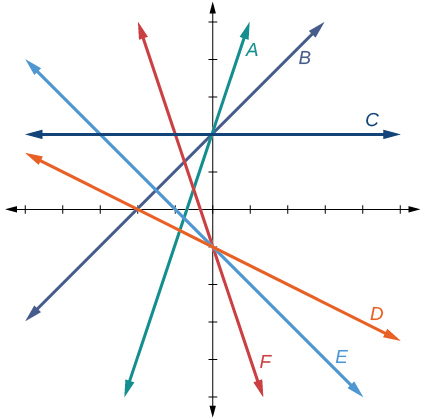
32) \(f(x)=−x−1\)
33) \(f(x)=−2x−1\)
- Answer
-
F
34) \(f(x)=−\dfrac{1}{2}x−1\)
35) \(f(x)=2\)
- Answer
-
C
36) \(f(x)=2+x\)
37) \(f(x)=3x+2\)
- Answer
-
A
For the exercises 38-43, sketch a line with the given features.
38) An \(x\)-intercept of \((–4, 0)\) and \(y\)-intercept of \((0, –2)\)
39) An \(x\)-intercept of \((–2, 0)\) and \(y\)-intercept of \((0, 4)\)
- Answer
-
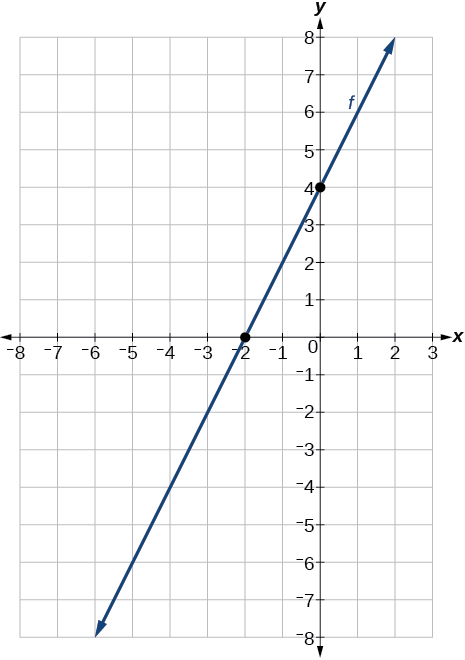
40) A \(y\)-intercept of \((0, 7)\) and slope \(−\dfrac{3}{2}\)
41) A \(y\)-intercept of \((0, 3)\) and slope \(\dfrac{2}{5}\)
- Answer
-
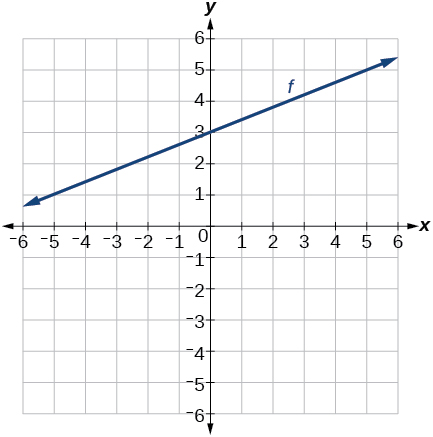
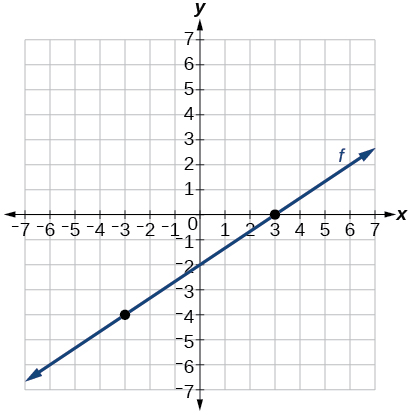
42) Passing through the points \((–6, –2)\) and \((6, –6)\)
43) Passing through the points \((–3, –4)\) and \((3, 0)\)
- Answer
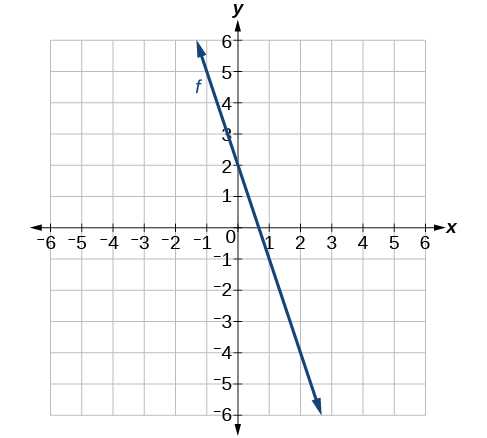
-
For the exercises 44-58, sketch the graph of each equation.
44) \(f(x)=−2x−1\)
45) \(g(x)=−3x+2\)
- Answer
-
46) \(h(x)=\dfrac{1}{3}x+2\)
47) \(k(x)=\dfrac{2}{3}x−3\)
- Answer
-
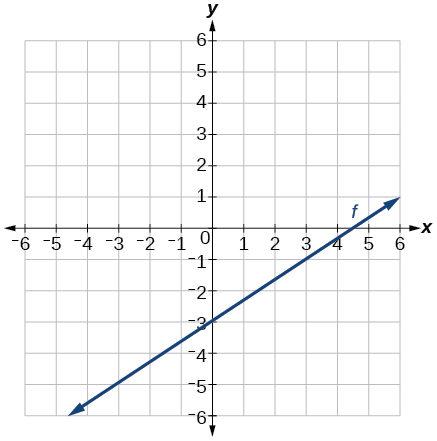
48) \(f(t)=3+2t\)
49) \(p(t)=−2 + 3t\)
- Answer
-
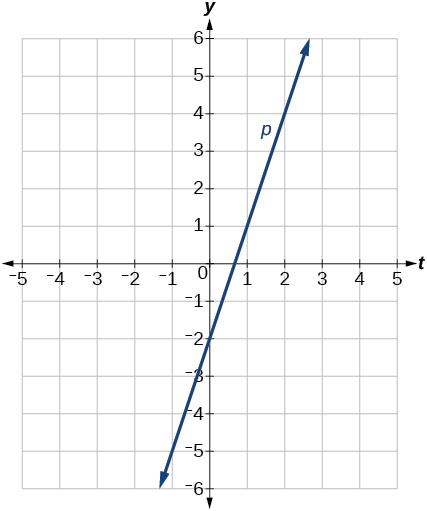
50) \(x=3\)
51) \(x=−2\)
- Answer
-
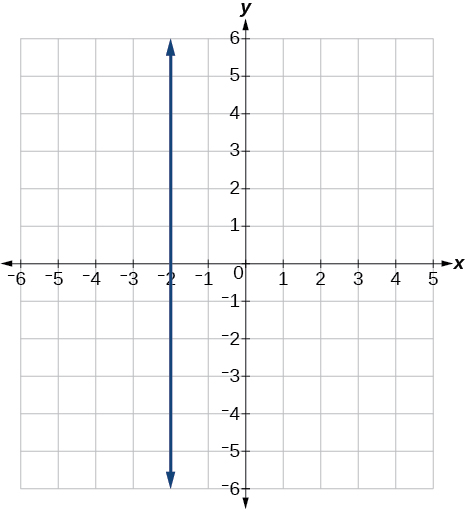
52) \(r(x)=4\)
53) \(q(x)=3\)
- Answer
-
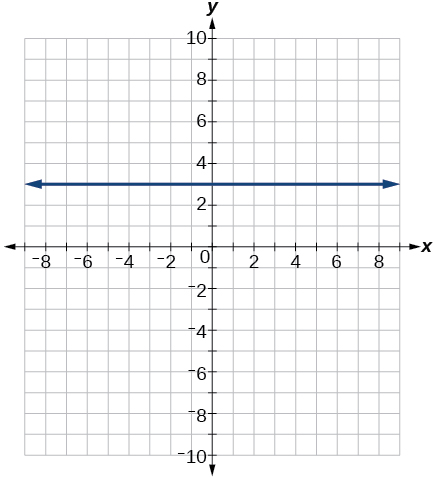
54) \(4x=−9y+36\)
55) \(\dfrac{x}{3}−\dfrac{y}{4}=1\)
- Answer
-
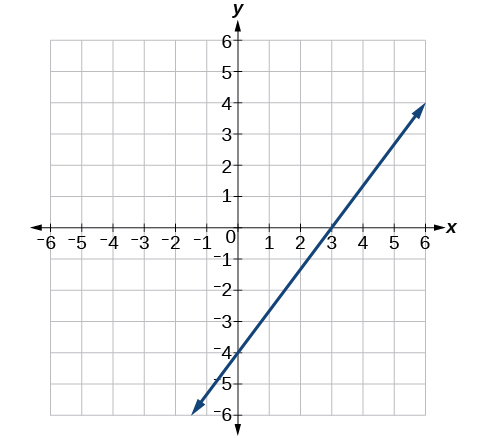
56) \(3x−5y=15\)
57) \(3x=15\)
- Answer
-
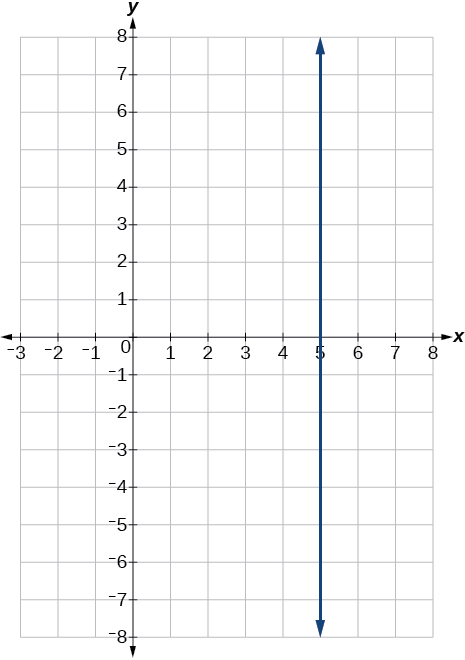
58) \(3y=12\)
59) If \(g(x)\) is the transformation of \(f(x)=x\) after a vertical compression by \(\dfrac{3}{4}\), a shift right by \(2\), and a shift down by \(4\)
- Write an equation for \(g(x)\).
- What is the slope of this line?
- Find the \(y\)-intercept of this line.
- Answer
-
- \(g(x)=0.75x−5.5\)
- \(0.75\)
- \(0,-5.5)\)
60) If \(g(x)\) is the transformation of \(f(x)=x\) after a vertical compression by \(\dfrac{1}{3}\), a shift left by \(1\), and a shift up by \(3\)
- Write an equation for \(g(x)\).
- What is the slope of this line?
- Find the \(y\)-intercept of this line.
For the exercises 61-64, write the equation of the line shown in the graph.
61)
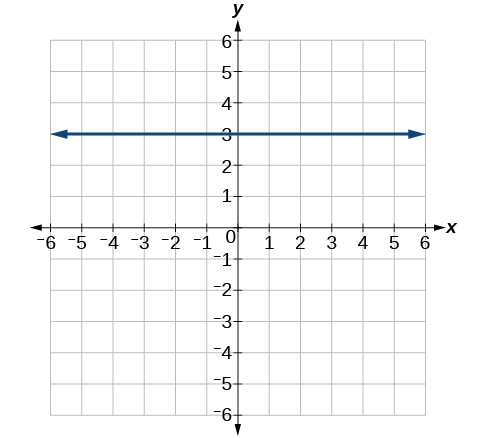
- Answer
-
\(y=3\)
62)
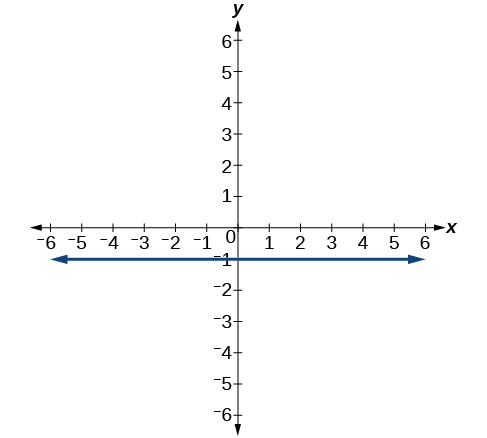
63)
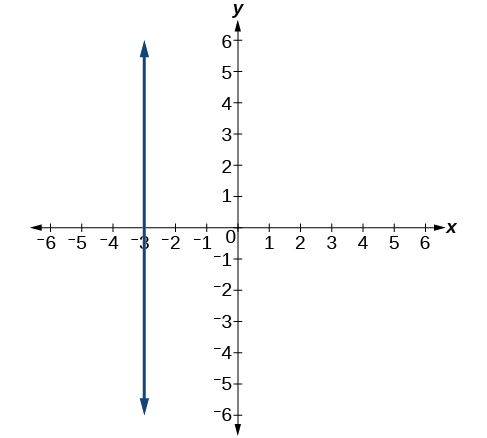
- Answer
-
\(x=−3\)
64)
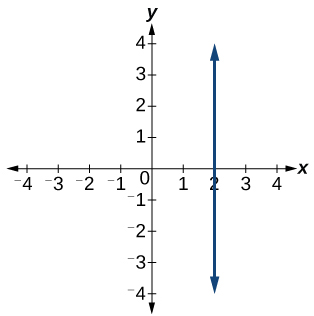
For the exercises 65-69, find the point of intersection of each pair of lines if it exists. If it does not exist, indicate that there is no point of intersection.
65) \(y=\dfrac{3}{4}x+1 \\ −3x+4y=12\)
- Answer
-
no point of intersection
66) \(2x−3y=12 \\ 5y+x=30\)
67) \(2x=y−3 \\ y+4x=15\)
- Answer
-
\((2, 7)\)
68) \(x−2y+2=3 \\ x−y=3 \)
69) \(5x+3y=−65 \\ x−y=−5 \)
- Answer
-
\((–10, –5)\)
Extensions
70) Find the equation of the line parallel to the line \(g(x)=−0.01x + 2.01\) through the point \((1, 2)\).
71) Find the equation of the line perpendicular to the line \(g(x)=−0.01x+2.01\) through the point \((1, 2)\).
- Answer
-
\(y=100x−98\)
For the exercises 72-73, use the functions \(f(x)=−0.1x+200\) and \(g(x)=20x+0.1\).
72) Find the point of intersection of the lines \(f\) and \(g\).
73) Where is \(f(x)\) greater than \(g(x)?\) Where is \(g(x)\) greater than \(f(x)?\)
- Answer
-
\(x<\dfrac{1999}{201}x>\dfrac{1999}{201}\)
Real-World Applications
74) A car rental company offers two plans for renting a car.
Plan A: \(\$30\) per day and \(\$0.18\) per mile
Plan B: \(\$50\) per day with free unlimited mileage
How many miles would you need to drive for plan B to save you money?
75) A cell phone company offers two plans for minutes.
Plan A: \(\$20\) per month and \(\$1\) for every one hundred texts.
Plan B: \(\$50\) per month with free unlimited texts.
How many texts would you need to send per month for plan B to save you money?
- Answer
-
Less than \(3000\) texts
76) A cell phone company offers two plans for minutes.
Plan A: \(\$15\) per month and \(\$2\) for every \(300\) texts.
Plan B: \(\$25\) per month and \(\$0.50\) for every \(100\) texts.
How many texts would you need to send per month for plan B to save you money?
2.3 Modeling with Linear Functions
Verbal
1) Explain how to find the input variable in a word problem that uses a linear function.
- Answer
-
Determine the independent variable. This is the variable upon which the output depends.
2) Explain how to find the output variable in a word problem that uses a linear function.
3) Explain how to interpret the initial value in a word problem that uses a linear function.
- Answer
-
To determine the initial value, find the output when the input is equal to zero.
4) Explain how to determine the slope in a word problem that uses a linear function.
Algebraic
5) Find the area of a parallelogram bounded by the \(y\) axis, the line \(x=3\), the line \(f(x)=1+2x\),and the line parallel to \(f(x)\) passing through (2, 7).
- Answer
-
\(6\) square units
6) Find the area of a triangle bounded by the \(x\)-axis, the line \(f(x)=12–\dfrac{1}{3}x\), and the line perpendicular to \(f(x)\) that passes through the origin.
7) Find the area of a triangle bounded by the \(y\)-axis, the line \(f(x)=9–\dfrac{6}{7}x\), and the line perpendicular to \(f(x)\) that passes through the origin.
- Answer
-
\(20.012\) square units
8) Find the area of a parallelogram bounded by the \(x\)-axis, the line \(g(x)=2\), the line \(f(x)=3x\), and the line parallel to \(f(x)\) passing through (6,1).
For the exercises 9-10, consider this scenario: A town’s population has been decreasing at a constant rate. In 2010 the population was \(5,900\). By 2012 the population had dropped \(4,700\). Assume this trend continues.
9) Predict the population in 2016.
- Answer
-
\(2,300\)
10) Identify the year in which the population will reach \(0\).
For the exercises 11-12, consider this scenario: A town’s population has been increased at a constant rate. In 2010 the population was \(46,020\). By 2012 the population had increased to \(52,070\). Assume this trend continues.
11) Predict the population in 2016.
- Answer
-
\(64,170\)
12) Identify the year in which the population will reach \(75,000\).
For the exercises 13-18, consider this scenario: A town has an initial population of \(75,000\). It grows at a constant rate of \(2,500\) per year for \(5\) years.
13) Find the linear function that models the town’s population \(P\) as a function of the year, \(t\), where \(t\) is the number of years since the model began.
- Answer
-
\(P(t)=75,000+2500t\)
14) Find a reasonable domain and range for the function \(P\).
15) If the function \(P\) is graphed, find and interpret the \(x\)- and \(y\)-intercepts.
- Answer
-
\((-30, 0)\) Thirty years before the start of this model, the town had no. \((0, 75,000)\) Initially, the town had a population of \(75,000\).
16) If the function \(P\) is graphed, find and interpret the slope of the function.
17) When will the output reached \(100,000\)?
- Answer
-
Ten years after the model began.
18) What is the output in the year \(12\) years from the onset of the model?
For the exercises 19-24, consider this scenario: The weight of a newborn is \(7.5\) pounds. The baby gained one-half pound a month for its first year.
19) Find the linear function that models the baby’s weight \(W\) as a function of the age of the baby, in months, \(t\).
- Answer
-
\(W(t)=7.5t+0.5\)
20) Find a reasonable domain and range for the function \(W\).
21) If the function \(W\) is graphed, find and interpret the \(x\)- and \(y\)-intercepts.
- Answer
-
\((−15,0)\): The \(x\)-intercept is not a plausible set of data for this model because it means the baby weighed \(0\) pounds \(15\) months prior to birth. \((0, 7.5)\): The baby weighed \(7.5\) pounds at birth.
22) If the function \(W\) is graphed, find and interpret the slope of the function.
23) When did the baby weight \(10.4\) pounds?
- Answer
-
At age \(5.8\) months.
24) What is the output when the input is \(6.2\)? Interpret your answer.
For the exercises 25-30, consider this scenario: The number of people afflicted with the common cold in the winter months steadily decreased by \(205\) each year from 2005 until 2010. In 2005, \(12,025\) people were afflicted.
25) Find the linear function that models the number of people inflicted with the common cold \(C\) as a function of the year, \(t\).
- Answer
-
\(C(t)=12,025−205t\)
26) Find a reasonable domain and range for the function \(C\).
27) If the function \(C\) is graphed, find and interpret the \(x\)- and \(y\)-intercepts.
- Answer
-
\((58.7, 0)\): In roughly \(59\) years, the number of people inflicted with the common cold would be \(0\). \((0,12,025)\): Initially there were \(12,025\) people afflicted by the common cold.
28) If the function \(C\) is graphed, find and interpret the slope of the function.
29) When will the output reach \(0\)?
- Answer
-
\(2064\)
30) In what year will the number of people be \(9,700\)?
Graphical
For the exercises 31-34, use the graph in the Figure below, which shows the profit, \(y\), in thousands of dollars, of a company in a given year, \(t\), where \(t\) represents the number of years since 1980.
.jpg?revision=1&size=bestfit&width=426&height=283)
31) Find the linear function \(y\), where \(y\) depends on \(t\), the number of years since 1980.
- Answer
-
\(y=−2t+180\)
32) Find and interpret the \(y\)-intercept.
33) Find and interpret the \(x\)-intercept.
- Answer
-
In 2070, the company’s profit will be zero.
34) Find and interpret the slope.
For the exercises 35-38, use the graph in the Figure below, which shows the profit, \(y\), in thousands of dollars, of a company in a given year, \(t\), where \(t\) represents the number of years since 1980.
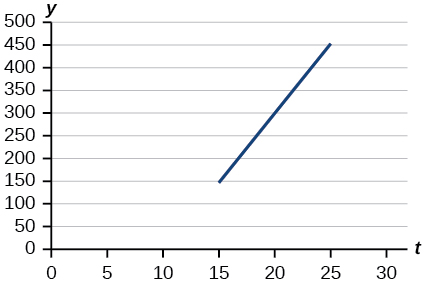
35) Find the linear function \(y\), where \(y\) depends on \(t\), the number of years since 1980.
- Answer
-
\(y=30t−300\)
36) Find and interpret the \(y\)-intercept.
37) Find and interpret the \(x\)-intercept.
- Answer
-
\((10, 0)\) In 1990, the profit earned zero profit.
38) Find and interpret the slope.
Numeric
For the exercises 39-41, use the median home values in Mississippi and Hawaii (adjusted for inflation) shown in the Table below. Assume that the house values are changing linearly.
| Year | Mississippi | Hawaii |
|---|---|---|
| 1950 | $25,200 | $74,400 |
| 2000 | $71,400 | $272,700 |
39) In which state have home values increased at a higher rate?
- Answer
-
Hawaii
40) If these trends were to continue, what would be the median home value in Mississippi in 2010?
41) If we assume the linear trend existed before 1950 and continues after 2000, the two states’ median house values will be (or were) equal in what year? (The answer might be absurd.)
- Answer
-
During the year 1933
For the exercises 42-44, use the median home values in Indiana and Alabama (adjusted for inflation) shown in the Table below. Assume that the house values are changing linearly.
| Year | Indiana | Alabama |
|---|---|---|
| 1950 | $37,700 | $27,100 |
| 2000 | $94,300 | $85,100 |
42) In which state have home values increased at a higher rate?
43) If these trends were to continue, what would be the median home value in Indiana in 2010?
- Answer
-
\(\$105,620\)
44) If we assume the linear trend existed before 1950 and continues after 2000, the two states’ median house values will be (or were) equal in what year? (The answer might be absurd.)
Real-World Applications
45) In 2004, a school population was \(1001\). By 2008 the population had grown to \(1697\). Assume the population is changing linearly.
- How much did the population grow between the year 2004 and 2008?
- How long did it take the population to grow from \(1001\) students to \(1697\) students?
- What is the average population growth per year?
- What was the population in the year 2000?
- Find an equation for the population, \(P\), of the school \(t\) years after 2000.
- Using your equation, predict the population of the school in 2011.
- Answer
-
- \(696\) people
- \(4\) years
- \(174\) people per year
- \(305\) people
- \(P(t)=305+174t\)
- \(2219\) people
46) In 2003, a town’s population was \(1431\). By 2007 the population had grown to \(2134\). Assume the population is changing linearly.
- How much did the population grow between the year 2003 and 2007?
- How long did it take the population to grow from \(1431\) people to \(2134\) people?
- What is the average population growth per year?
- What was the population in the year 2000?
- Find an equation for the population, \(P\) of the town \(t\) years after 2000.
- Using your equation, predict the population of the town in 2014.
47) A phone company has a monthly cellular plan where a customer pays a flat monthly fee and then a certain amount of money per minute used on the phone. If a customer uses \(410\) minutes, the monthly cost will be \(\$71.50\). If the customer uses \(720\) minutes, the monthly cost will be \(\$118\).
- Interpret the slope and \(y\)-intercept of the equation.
- Use your equation to find the total monthly cost if \(687\) minutes are used.
- Answer
-
- \(C(x)=0.15x+10\)
- The flat monthly fee is \(\$10\) and there is an additional \(\$0.15\) fee for each additional minute used
- \(\$113.05\)
48) A phone company has a monthly cellular data plan where a customer pays a flat monthly fee of \(\$10\) and then a certain amount of money per megabyte (MB) of data used on the phone. If a customer uses \(20\) MB, the monthly cost will be \(\$11.20\). If the customer uses \(130\) MB, the monthly cost will be \(\$17.80\).
- Interpret the slope and \(y\)-intercept of the equation.
- Use your equation to find the total monthly cost if \(250\) MB are used.
49) In 1991, the moose population in a park was measured to be \(4,360\). By 1999, the population was measured again to be \(5,880\). Assume the population continues to change linearly.
- What does your model predict the moose population to be in 2003?
- Answer
-
- \(P(t)=190t+4360\)
- \(6640\) moose
50) In 2003, the owl population in a park was measured to be \(340\). By 2007, the population was measured again to be \(285\). The population changes linearly. Let the input be years since 1990.
- What does your model predict the owl population to be in 2012?
51) The Federal Helium Reserve held about \(16\) billion cubic feet of helium in 2010 and is being depleted by about \(2.1\) billion cubic feet each year.
- In 2015, what will the helium reserves be?
- If the rate of depletion doesn’t change, in what year will the Federal Helium Reserve be depleted?
- Answer
-
- \(R(t)=16−2.1t\)
- \(5.5\) billion cubic feet
- During the year 2017
52) Suppose the world’s oil reserves in 2014 are \(1,820\) billion barrels. If, on average, the total reserves are decreasing by \(25\) billion barrels of oil each year:
- Seven years from now, what will the oil reserves be?
- If the rate at which the reserves are decreasing is constant, when will the world’s oil reserves be depleted?
53) You are choosing between two different prepaid cell phone plans. The first plan charges a rate of \(26\) cents per minute. The second plan charges a monthly fee of \(\$19.95\) plus \(11\) cents per minute. How many minutes would you have to use in a month in order for the second plan to be preferable?
- Answer
-
More than \(133\) minutes
54) You are choosing between two different window washing companies. The first charges \(\$5\) per window. The second charges a base fee of \(\$40\) plus \(\$3\) per window. How many windows would you need to have for the second company to be preferable?
55) When hired at a new job selling jewelry, you are given two pay options:
Option A: Base salary of \(\$17,000\) a year with a commission of \(12\%\) of your sales
Option B: Base salary of \(\$20,000\) a year with a commission of \(5\%\) of your sales
How much jewelry would you need to sell for option A to produce a larger income?
- Answer
-
More than \(\$42,857.14\) worth of jewelry
56) When hired at a new job selling electronics, you are given two pay options:
Option A: Base salary of \(\$14,000\) a year with a commission of \(10\%\) of your sales
Option B: Base salary of \(\$19,000\) a year with a commission of \(4\%\) of your sales
How much electronics would you need to sell for option A to produce a larger income?
57) When hired at a new job selling electronics, you are given two pay options:
Option A: Base salary of \(\$20,000\) a year with a commission of \(12\%\) of your sales
Option B: Base salary of \(\$26,000\) a year with a commission of \(3\%\) of your sales
How much electronics would you need to sell for option A to produce a larger income?
- Answer
-
\(\$66,666.67\)
58) When hired at a new job selling electronics, you are given two pay options:
Option A: Base salary of \(\$10,000\) a year with a commission of \(9\%\) of your sales
Option B: Base salary of \(\$20,000\) a year with a commission of \(4\%\) of your sales
How much electronics would you need to sell for option A to produce a larger income?
2.4 Fitting Linear Models to Data
Verbal
1) Describe what it means if there is a model breakdown when using a linear model.
- Answer
-
When our model no longer applies, after some value in the domain, the model itself doesn’t hold.
2) What is interpolation when using a linear model?
3) What is extrapolation when using a linear model?
- Answer
-
We predict a value outside the domain and range of the data.
4) Explain the difference between a positive and a negative correlation coefficient.
5) Explain how to interpret the absolute value of a correlation coefficient.
- Answer
-
The closer the number is to \(1\), the less scattered the data, the closer the number is to \(0\), the more scattered the data.
Algebraic
6) A regression was run to determine whether there is a relationship between hours of TV watched per day (x) and number of sit-ups a person can do (y). The results of the regression are given below. Use this to predict the number of sit-ups a person who watches \(11\) hours of TV can do.
\[\begin{array}{l}{y=a x+b} \\ {a=-1.341} \\ {b=32.234} \\ {r=-0.896}\end{array}\nonumber\]
7) A regression was run to determine whether there is a relationship between the diameter of a tree (\(x\),in inches) and the tree’s age (\(y\),in years). The results of the regression are given below. Use this to predict the age of a tree with diameter \(10\) inches. \[\begin{array}{l}{y=a x+b} \\ {a=6.301} \\ {b=-1.044} \\ {r=-0.970}\end{array}\nonumber\]
- Answer
-
\(61.966\) years
For the exercises 8-11, draw a scatter plot for the data provided. Does the data appear to be linearly related?
8)
| 0 | 2 | 4 | 6 | 8 | 10 |
| –22 | –19 | –15 | –11 | –6 | –2 |
9)
| 1 | 2 | 3 | 4 | 5 | 6 |
| 46 | 50 | 59 | 75 | 100 | 136 |
- Answer
-
No
10)
| 100 | 250 | 300 | 450 | 600 | 750 |
| 12 | 12.6 | 13.1 | 14 | 14.5 | 15.2 |
11)
| 1 | 3 | 5 | 7 | 9 | 11 |
| 1 | 9 | 28 | 65 | 125 | 216 |
- Answer
-
No
12) For the following data, draw a scatter plot. If we wanted to know when the population would reach \(15,000\), would the answer involve interpolation or extrapolation? Eyeball the line, and estimate the answer.
| Year | Population |
|---|---|
| 1990 | 11,500 |
| 1995 | 12,100 |
| 2000 | 12,700 |
| 2005 | 13,000 |
| 2010 | 13,750 |
13) For the following data, draw a scatter plot. If we wanted to know when the temperature would reach \(28^{\circ} F\), would the answer involve interpolation or extrapolation? Eyeball the line and estimate the answer.
| Temperature, °F | 16 | 18 | 20 | 25 | 30 |
| Time, seconds | 46 | 50 | 54 | 55 | 62 |
- Answer
-
Interpolation. About \(60° F\).
Graphical
For the exercises 14-17, match each scatterplot with one of the four specified correlations in Figure ab and Figure cd.
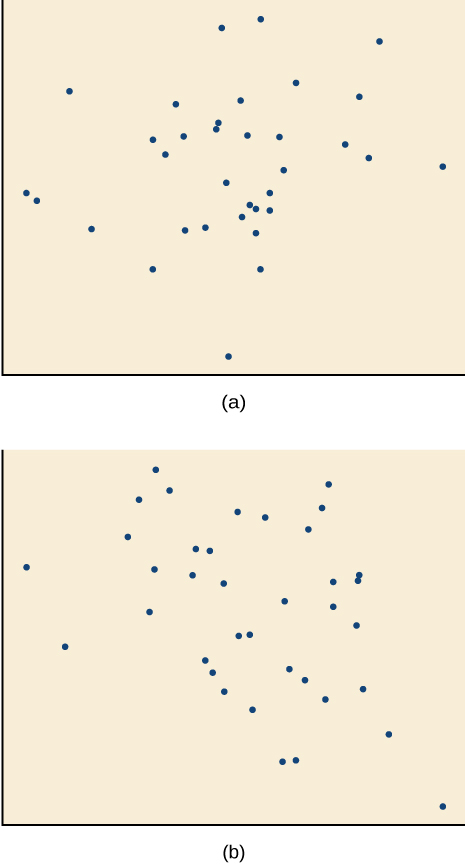
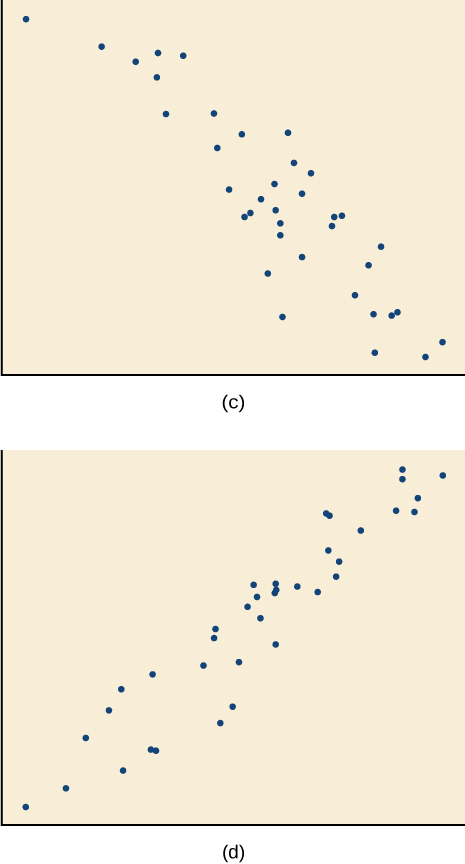
14) \(r=0.95\)
15) \(r=−0.89\)
- Answer
-
C
16) \(r=0.26\)
17) \(r=−0.39\)
- Answer
-
B
For the exercises 18-21, draw a best-fit line for the plotted data.
18)
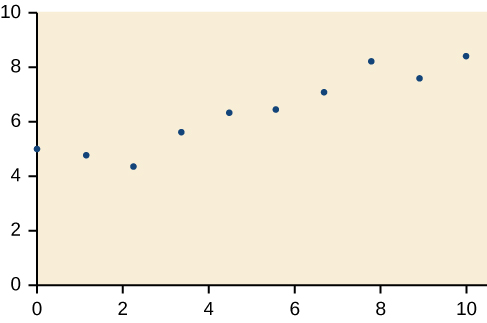
19)
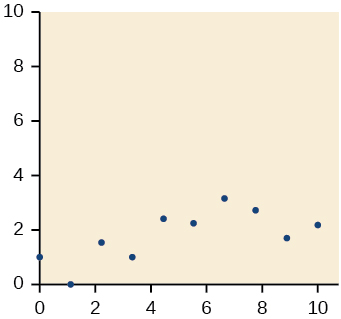
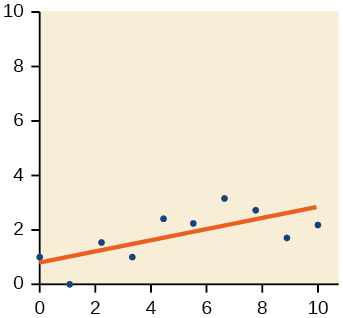
- Answer
-
20)
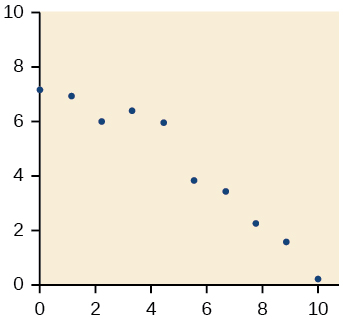
21)
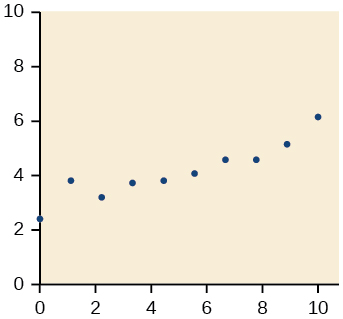
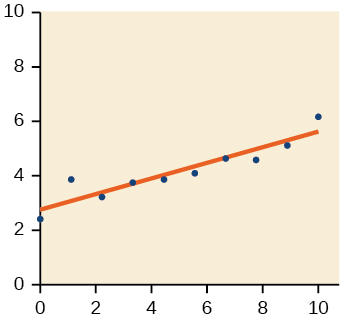
- Answer
-
Numeric
22) The U.S. Census tracks the percentage of persons \(25\) years or older who are college graduates. That data for several years is given in the Table below. Determine whether the trend appears linear. If so, and assuming the trend continues, in what year will the percentage exceed \(35\%\)?
| Year | Percent Graduates |
|---|---|
| 1990 | 21.3 |
| 1992 | 21.4 |
| 1994 | 22.2 |
| 1996 | 23.6 |
| 1998 | 24.4 |
| 2000 | 25.6 |
| 2002 | 26.7 |
| 2004 | 27.7 |
| 2006 | 28 |
| 2008 | 29.4 |
23) The U.S. import of wine (in hectoliters) for several years is given in the Table. Determine whether the trend appears linear. If so, and assuming the trend continues, in what year will imports exceed \(12,000\) hectoliters?
| Year | Imports |
|---|---|
| 1992 | 2665 |
| 1994 | 2688 |
| 1996 | 3565 |
| 1998 | 4129 |
| 2000 | 4584 |
| 2002 | 5655 |
| 2004 | 6549 |
| 2006 | 7950 |
| 2008 | 8487 |
| 2009 | 9462 |
- Answer
-
Yes, trend appears linear because \(r=0.985\) and will exceed \(12,000\) near midyear, 2016, \(24.6\) years since 1992.
24) The Table shows the year and the number of people unemployed in a particular city for several years. Determine whether the trend appears linear. If so, and assuming the trend continues, in what year will the number of unemployed reach \(5\)?
| Year | Number Unemployed |
|---|---|
| 1990 | 750 |
| 1992 | 670 |
| 1994 | 650 |
| 1996 | 605 |
| 1998 | 550 |
| 2000 | 510 |
| 2002 | 460 |
| 2004 | 420 |
| 2006 | 380 |
| 2008 | 320 |
Technology
For the exercises 25-31, use each set of data to calculate the regression line using a calculator or other technology tool, and determine the correlation coefficient to \(3\) decimal places of accuracy.
25)
| \(x\) | 8 | 15 | 26 | 31 | 56 |
|---|---|---|---|---|---|
| \(y\) | 23 | 41 | 53 | 72 | 103 |
- Answer
-
\(y=1.640x+13.800, r=0.987\)
26)
| \(x\) | 5 | 7 | 10 | 12 | 15 |
|---|---|---|---|---|---|
| \(y\) | 4 | 12 | 17 | 22 | 24 |
27)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| 3 | 21.9 | 11 | 15.76 |
| 4 | 22.22 | 12 | 13.68 |
| 5 | 22.74 | 13 | 14.1 |
| 6 | 22.26 | 14 | 14.02 |
| 7 | 20.78 | 15 | 11.94 |
| 8 | 17.6 | 16 | 12.76 |
| 9 | 16.52 | 17 | 11.28 |
| 10 | 18.54 | 18 | 9.1 |
- Answer
-
\(y=−0.962x+26.86, r=−0.965\)
28)
| \(x\) | \(y\) |
|---|---|
| 4 | 44.8 |
| 5 | 43.1 |
| 6 | 38.8 |
| 7 | 39 |
| 8 | 38 |
| 9 | 32.7 |
| 10 | 30.1 |
| 11 | 29.3 |
| 12 | 27 |
| 13 | 25.8 |
29)
| \(x\) | \(y\) |
|---|---|
| 21 | 17 |
| 25 | 11 |
| 30 | 2 |
| 31 | −1 |
| 40 | −18 |
| 50 | −40 |
- Answer
-
\(y=−1.981x+60.197; r=−0.998\)
30)
| \(x\) | \(y\) |
|---|---|
| 100 | 2000 |
| 80 | 1798 |
| 60 | 1589 |
| 55 | 1580 |
| 40 | 1390 |
| 20 | 1202 |
31)
| \(x\) | \(y\) |
|---|---|
| 900 | 70 |
| 988 | 80 |
| 1000 | 82 |
| 1010 | 84 |
| 1200 | 105 |
| 1205 | 108 |
- Answer
-
\(y=0.121x−38.841, r=0.998\)
Extensions
32) Graph \(f(x)=0.5x+10\). Pick a set of \(5\) ordered pairs using inputs \(x=−2, 1, 5, 6, 9\) and use linear regression to verify that the function is a good fit for the data.
33) Graph \(f(x)=−2x−10\). Pick a set of \(5\) ordered pairs using inputs \(x=−2, 1, 5, 6, 9\) and use linear regression to verify the function.
- Answer
-
\((−2,−6),(1,−12),(5,−20),(6,−22),(9,−28); y=−2x−10\)
For the exercises 34-36, consider this scenario: The profit of a company decreased steadily over a ten-year span. The following ordered pairs shows dollars and the number of units sold in hundreds and the profit in thousands of over the ten-year span, (number of units sold, profit) for specific recorded years:
\[(46, 1,600), (48, 1,550), (50, 1,505), (52, 1,540), (54, 1,495) \nonumber\]
34) Use linear regression to determine a function \(P\) where the profit in thousands of dollars depends on the number of units sold in hundreds.
35) Find to the nearest tenth and interpret the \(x\)-intercept.
- Answer
-
\((189.8,0)\) If \(18,980\) units are sold, the company will have a profit of zero dollars.
36) Find to the nearest tenth and interpret the \(y\)-intercept.
Real-World Applications
For the exercises 37-38, consider this scenario: The population of a city increased steadily over a ten-year span. The following ordered pairs shows the population and the year over the ten-year span, (population, year) for specific recorded years:
\[(2500, 2000), (2650, 2001), (3000, 2003), (3500, 2006), (4200, 2010) \nonumber \]
37) Use linear regression to determine a function \(y\), where the year depends on the population. Round to three decimal places of accuracy.
- Answer
-
\(y=0.00587x+1985.41\)
38) Predict when the population will hit \(8,000\).
For the exercises 39-40, consider this scenario: The profit of a company increased steadily over a ten-year span. The following ordered pairs show the number of units sold in hundreds and the profit in thousands of over the ten year span, (number of units sold, profit) for specific recorded years:
\[(46, 250), (48, 305), (50, 350), (52, 390), (54, 410) \nonumber \]
39) Use linear regression to determine a function \(y\), where the profit in thousands of dollars depends on the number of units sold in hundreds.
- Answer
-
\(y=20.25x−671.5\)
40) Predict when the profit will exceed one million dollars.
For the exercises 41-42, consider this scenario: The profit of a company decreased steadily over a ten-year span. The following ordered pairs show dollars and the number of units sold in hundreds and the profit in thousands of over the ten-year span (number of units sold, profit) for specific recorded years:
\[(46, 250), (48, 225), (50, 205), (52, 180), (54, 165) \nonumber\]
41) Use linear regression to determine a function \(y\), where the profit in thousands of dollars depends on the number of units sold in hundreds.
- Answer
-
\(y=−10.75x+742.50\)
42) Predict when the profit will dip below the \(\$25,000\) threshold.


