10.E: Analytic Geometry (Exercises)
- Page ID
- 17851
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)10.1: The Ellipse
In this section, we will investigate the shape of this room and its real-world applications, including how far apart two people in Statuary Hall can stand and still hear each other whisper.
Verbal
1) Define an ellipse in terms of its foci.
- Answer
-
An ellipse is the set of all points in the plane the sum of whose distances from two fixed points, called the foci, is a constant.
2) Where must the foci of an ellipse lie?
3) What special case of the ellipse do we have when the major and minor axis are of the same length?
- Answer
-
This special case would be a circle.
4) For the special case mentioned above, what would be true about the foci of that ellipse?
5) What can be said about the symmetry of the graph of an ellipse with center at the origin and foci along the \(y\)-axis?
- Answer
-
It is symmetric about the \(x\)-axis, \(y\)-axis, and the origin.
Algebraic
For the exercises 6-10, determine whether the given equations represent ellipses. If yes, write in standard form.
6) \(2x^2 +y=4\)
7) \(4x^2 + 9y^2=36\)
- Answer
-
yes; \(\dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1\)
8) \(4x^2 - y^2=4\)
9) \(4x^2 + 9y^2=1\)
- Answer
-
yes; \(\dfrac{x^2}{\left (\tfrac{1}{2} \right )^2}+\dfrac{y^2}{\left (\tfrac{1}{2} \right )^2}=1\)
10) \(4x^2-8x+9y^2-72y+112=0\)
For the exercises 11-26, write the equation of an ellipse in standard form, and identify the end points of the major and minor axes as well as the foci.
11) \(\dfrac{x^2}{4}+\dfrac{y^2}{49}=1\)
- Answer
-
\(\dfrac{x^2}{2^2}+\dfrac{y^2}{7^2}=1\); Endpoints of major axis \((0,7)\) and \((0,-7)\). Endpoints of minor axis \((2,0)\) and \((-2,0)\). Foci at \((0, 3\sqrt{5})\), \((0, -3\sqrt{5})\).
12) \(\dfrac{x^2}{100}+\dfrac{y^2}{64}=1\)
13) \(x^2 + 9y^2 = 1\)
- Answer
-
\(\dfrac{x^2}{(1)^2}+\dfrac{y^2}{\left (\tfrac{1}{3} \right )^2}=1\); Endpoints of major axis \((1,0)\) and \((-1,0)\). Endpoints of minor axis \(\left (0, \dfrac{1}{3} \right )\), \(\left (0, -\dfrac{1}{3} \right )\). Foci at \(\left (\dfrac{2\sqrt{2}}{3}, 0 \right )\), \(\left (-\dfrac{2\sqrt{2}}{3}, 0 \right )\).
14) \(4x^2 + 16y^2 = 1\)
15) \(\dfrac{(x-2)^2}{49}+\dfrac{(y-4)^2}{25}=1\)
- Answer
-
\(\dfrac{(x-2)^2}{7^2}+\dfrac{(y-4)^2}{5^2}=1\); Endpoints of major axis \((9,4)\), \((-5,4)\). Endpoints of minor axis \((2,9)\), \((2,-1)\). Foci at \((2+2\sqrt{6}, 4)\), \((2-2\sqrt{6}, 4)\)
16) \(\dfrac{(x-2)^2}{81}+\dfrac{(y+1)^2}{16}=1\)
17) \(\dfrac{(x+5)^2}{4}+\dfrac{(y-7)^2}{9}=1\)
- Answer
-
\(\dfrac{(x+5)^2}{2^2}+\dfrac{(y-7)^2}{3^2}=1\); Endpoints of major axis \((-5,10)\), \((-5,4)\). Endpoints of minor axis \((-3,7)\), \((-7,7)\). Foci at \((-5, 7+\sqrt{5})\), \((-5, 7-\sqrt{5})\)
18) \(\dfrac{(x-7)^2}{49}+\dfrac{(y-7)^2}{49}=1\)
19) \(4x^2-8x+9y^2-72y+112=0\)
- Answer
-
\(\dfrac{(x-1)^2}{3^2}+\dfrac{(y-4)^2}{2^2}=1\); Endpoints of major axis \((4,4)\), \((-2,4)\). Endpoints of minor axis \((1,6)\), \((1,2)\). Foci at \((1+\sqrt{5}, 4)\), \((1-\sqrt{5}, 4)\)
20) \(9x^2-54x+9y^2-54y+81=0\)
21) \(4x^2-24x+36y^2-360y+864=0\)
- Answer
-
\(\dfrac{(x-3)^2}{(3\sqrt{2})^2}+\dfrac{(y-5)^2}{\sqrt{2}^2}=1\); Endpoints of major axis \((3+3\sqrt{2}, 5)\), \((3-3\sqrt{2}, 5)\). Endpoints of minor axis \((3, 5+\sqrt{2})\), \((3, 5-\sqrt{2})\). Foci at \((7,5)\), \((-1,5)\)
22) \(4x^2+24x+16y^2-128y+228=0\)
23) \(4x^2+40x+25y^2-100y+100=0\)
- Answer
-
\(\dfrac{(x+5)^2}{(5)^2}+\dfrac{(y-2)^2}{(2)^2}=1\); Endpoints of major axis \((0,2)\), \((-10,2)\). Endpoints of minor axis \((-5,4)\), \((-5,0)\). Foci at \((-5+\sqrt{21}, 2)\), \((-5-\sqrt{21}, 2)\)
24) \(x^2+2x+100y^2-1000y+2401=0\)
25) \(4x^2+24x+25y^2+200y+336=0\)
- Answer
-
\(\dfrac{(x+3)^2}{(5)^2}+\dfrac{(y+4)^2}{(2)^2}=1\); Endpoints of major axis \((2,-4)\), \((-8,-4)\). Endpoints of minor axis \((-3,-2)\), \((-3,-6)\). Foci at \((-3+\sqrt{21}, -4)\), \((-3-\sqrt{21}, -4)\)
26) \(9x^2+72x+16y^2+16y+4=0\)
For the exercises 27-31, find the foci for the given ellipses.
27) \(\dfrac{(x+3)^2}{25}+\dfrac{(y+1)^2}{36}=1\)
- Answer
-
Foci \((-3, -1+\sqrt{11})\), \((-3, -1-\sqrt{11})\)
28) \(\dfrac{(x+1)^2}{100}+\dfrac{(y-2)^2}{4}=1\)
29) \(x^2+y^2=1\)
- Answer
-
Focus \((0,0)\)
30) \(x^2+4y^2+4x+8y=1\)
31) \(10x^2+y^2+200x=0\)
- Answer
-
Foci \((-10,30)\), \((-10,-30)\)
Graphical
For the exercises 32-45, graph the given ellipses, noting center, vertices, and foci.
32) \(\dfrac{x^2}{25}+\dfrac{y^2}{36}=1\)
33) \(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\)
- Answer
-
Center \((0,0)\), Vertices \((4,0)\), \((-4,0)\), \((0,3)\), \((0,-3)\). Foci \((\sqrt{7},0)\), \((-\sqrt{7},0)\)
34) \(4x^2+9y^2=1\)
35) \(81x^2+49y^2=1\)
- Answer
-
Center \((0,0)\), Vertices \(\left ( \dfrac{1}{9}, 0 \right )\), \(\left ( -\dfrac{1}{9}, 0 \right )\), \(\left ( 0, \dfrac{1}{7} \right )\), \(\left ( 0, \dfrac{1}{7} \right )\). Foci \(\left ( 0, \dfrac{4\sqrt{2}}{63} \right )\), \(\left ( 0, -\dfrac{4\sqrt{2}}{63} \right )\)
36) \(\dfrac{(x-2)^2}{64}+\dfrac{(y-4)^2}{16}=1\)
37) \(\dfrac{(x+3)^2}{9}+\dfrac{(y-3)^2}{9}=1\)
- Answer
-
Center \((-3,3)\), Vertices \((0,3)\), \((-6,3)\), \((-3,0)\), \((-3,6)\). Focus \((-3,3)\)
Note that this ellipse is a circle. The circle has only one focus, which coincides with the center.
38) \(\dfrac{x^2}{2}+\dfrac{(y+1)^2}{5}=1\)
39) \(4x^2-8x+16y^2-32y-44=0\)
- Answer
-
Center \((1,1)\), Vertices \((5,1)\), \((-3,1)\), \((1,3)\), \((1,-1)\). Foci \((1,1+4\sqrt{3})\), \((1,1-4\sqrt{3})\)
40) \(x^2-8x+25y^2-100y+91=0\)
41) \(x^2+8x+4y^2-40y+112=0\)
- Answer
-
Center \((-4,5)\), Vertices \((-2,5)\), \((-6,4)\), \((-4,6)\), \((-4,4)\). Foci \((-4+\sqrt{3}, 5)\), \((-4-4\sqrt{3}, 5)\)
42) \(64x^2+128x+9y^2-72y-368=0\)
43) \(16x^2+64x+4y^2-8y+4=0\)
- Answer
-
Center \((-2,1)\), Vertices \((0,1)\), \((-4,1)\), \((-2,5)\), \((-2,-3)\). Foci \((-2,1+2\sqrt{3})\), \((-2,1-2\sqrt{3})\)
44) \(100x^2+1000x+y^2-10y+2425=0\)
45) \(4x^2+16x+4y^2+16y+16=0\)
- Answer
-
Center \((-2,2)\), Vertices \((0,-2)\), \((-4,-2)\), \((-2,0)\), \((-2,-4)\). Focus \((-2,-2)\)
For the exercises 46-51, use the given information about the graph of each ellipse to determine its equation.
46) Center at the origin, symmetric with respect to the \(x\)- and \(y\)-axes, focus at \((4,0)\) and point on graph \((0,3)\).
47) Center at the origin, symmetric with respect to the \(x\)- and \(y\)-axes, focus at \((0,-2)\) and point on graph \((5,0)\).
- Answer
-
\(\dfrac{x^2}{25}+\dfrac{y^2}{29}=1\)
48) Center at the origin, symmetric with respect to the \(x\)- and \(y\)-axes, focus at \((3,0)\), and major axis is twice as long as minor axis.
49) Center \((4,2)\); vertex \((9,2)\); one focus: \((4+2\sqrt{6}, 2)\)
- Answer
-
\(\dfrac{(x-4)^2}{25}+\dfrac{(y-2)^2}{1}=1\)
50) Center \((3,5)\); vertex \((3,11)\); one focus: \((3, 5+4\sqrt{2})\)
51) Center \((-3,4)\); vertex \((1,4)\); one focus: \((-3+2\sqrt{3}, 4)\)
- Answer
-
\(\dfrac{(x+3)^2}{16}+\dfrac{(y-4)^2}{4}=1\)
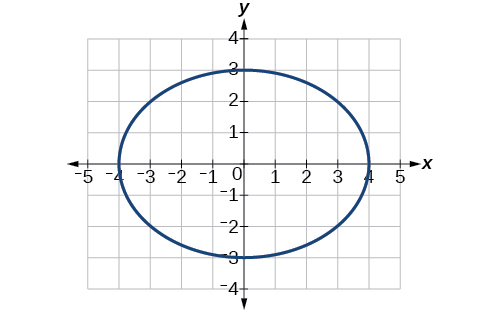
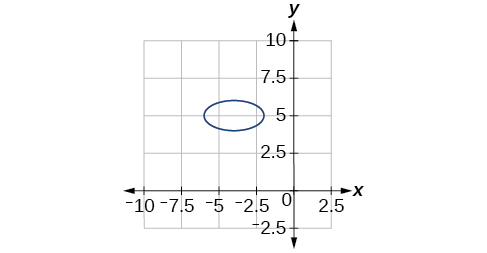
For the exercises 52-56, given the graph of the ellipse, determine its equation.
52)
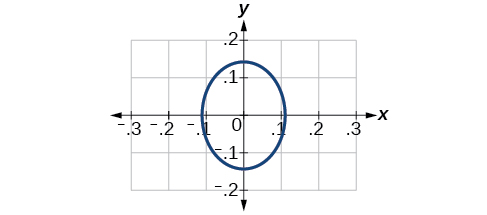
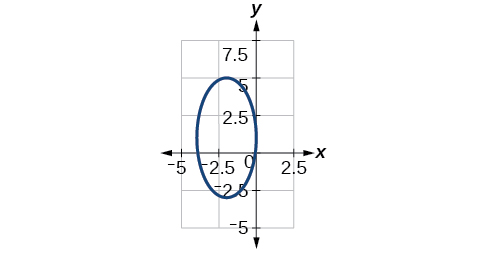
53)
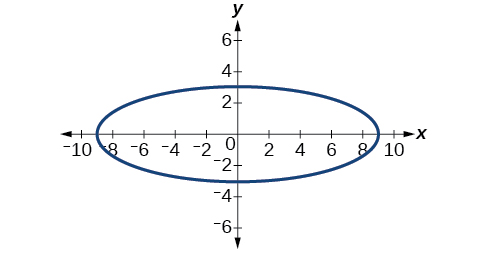
- Answer
-
\(\dfrac{x^2}{81}+\dfrac{y^2}{9}=1\)
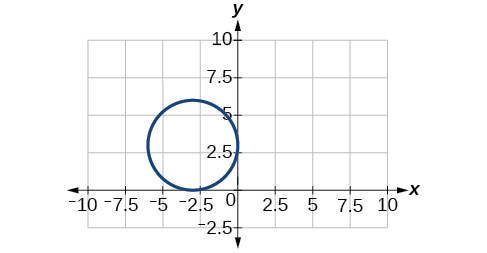
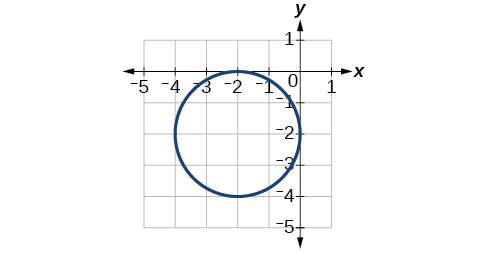
54)
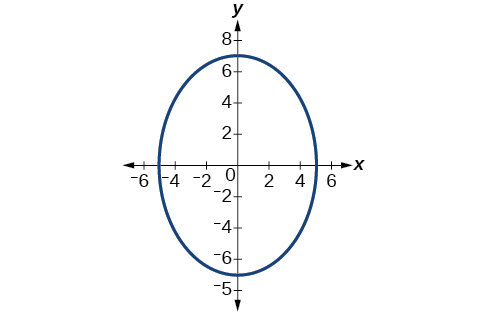
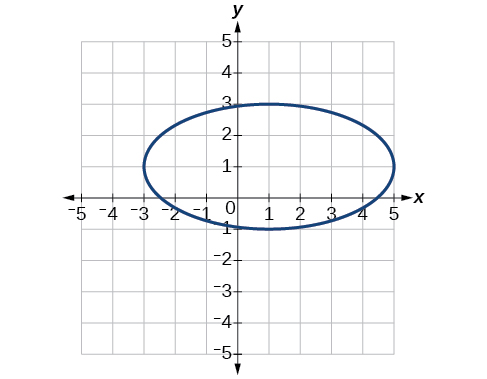
55)
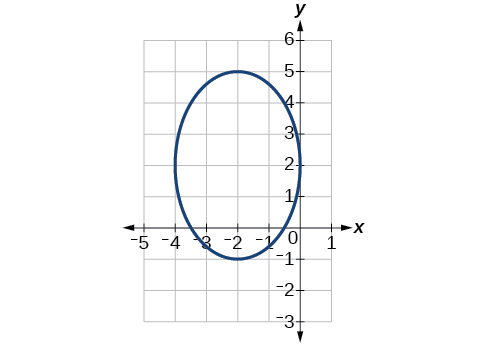
- Answer
-
\(\dfrac{(x+2)^2}{4}+\dfrac{(y-2)^2}{9}=1\)
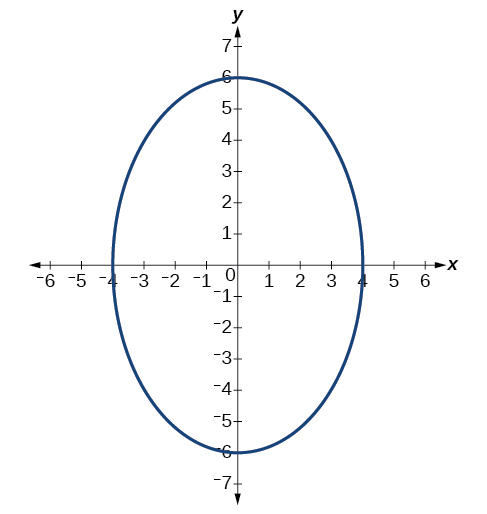
56)
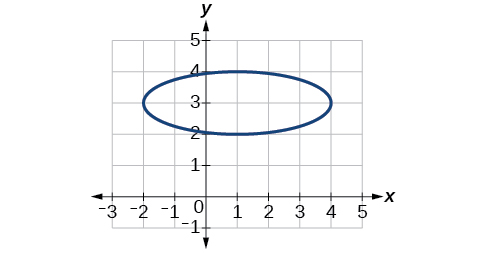
Extensions
For the exercises 57-61, find the area of the ellipse. The area of an ellipse is given by the formula \(\text {Area}=a\cdot b\cdot \pi\)
57) \(\dfrac{(x-3)^2}{9}+\dfrac{(y-3)^2}{16}=1\)
- Answer
-
\(\text {Area} = 12\pi \) square units
58) \(\dfrac{(x+6)^2}{16}+\dfrac{(y-6)^2}{36}=1\)
59) \(\dfrac{(x+1)^2}{4}+\dfrac{(y-2)^2}{5}=1\)
- Answer
-
\(\text {Area} = 2\sqrt{5} \pi \) square units
60) \(4x^2-8x+9y^2-72y+112=0\)
61) \(9x^2-54x+9y^2-54y+81=0\)
- Answer
-
\(\text {Area} = 9\pi \) square units
Real-World Applications
62) Find the equation of the ellipse that will just fit inside a box that is \(8\) units wide and \(4\) units high.
63) Find the equation of the ellipse that will just fit inside a box that is four times as wide as it is high. Express in terms of \(h\), the height.
- Answer
-
\(\dfrac{x^2}{4h^2}+\dfrac{y^2}{\tfrac{1}{4}h^2}=1\)
64) An arch has the shape of a semi-ellipse (the top half of an ellipse). The arch has a height of \(8\) feet and a span of \(20\) feet. Find an equation for the ellipse, and use that to find the height to the nearest \(0.01\) foot of the arch at a distance of \(4\) feet from the center.
65) An arch has the shape of a semi-ellipse. The arch has a height of \(12\) feet and a span of \(40\) feet. Find an equation for the ellipse, and use that to find the distance from the center to a point at which the height is \(6\) feet. Round to the nearest hundredth.
- Answer
-
\(\dfrac{x^2}{400}+\dfrac{y^2}{144}=1\). Distance = \(17.32\) feet
66) A bridge is to be built in the shape of a semi-elliptical arch and is to have a span of \(120\) feet. The height of the arch at a distance of \(40\) feet from the center is to be \(8\) feet. Find the height of the arch at its center.
67) A person in a whispering gallery standing at one focus of the ellipse can whisper and be heard by a person standing at the other focus because all the sound waves that reach the ceiling are reflected to the other person. If a whispering gallery has a length of \(120\) feet, and the foci are located \(30\) feet from the center, find the height of the ceiling at the center.
- Answer
-
Approximately \(51.96\) feet
68) A person is standing \(8\) feet from the nearest wall in a whispering gallery. If that person is at one focus, and the other focus is \(80\) feet away, what is the length and height at the center of the gallery?
10.2: The Hyperbola
In analytic geometry, a hyperbola is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected. This intersection produces two separate unbounded curves that are mirror images of each other.
Verbal
1) Define a hyperbola in terms of its foci.
- Answer
-
A hyperbola is the set of points in a plane the difference of whose distances from two fixed points (foci) is a positive constant.
2) What can we conclude about a hyperbola if its asymptotes intersect at the origin?
3) What must be true of the foci of a hyperbola?
- Answer
-
The foci must lie on the transverse axis and be in the interior of the hyperbola.
4) If the transverse axis of a hyperbola is vertical, what do we know about the graph?
5) Where must the center of hyperbola be relative to its foci?
- Answer
-
The center must be the midpoint of the line segment joining the foci.
Algebraic
For the exercises 6-10, determine whether the following equations represent hyperbolas. If so, write in standard form.
6) \(3y^2 + 2x = 6\)
7) \(\dfrac{x^2}{36}-\dfrac{y^2}{9}=1\)
- Answer
-
yes \(\dfrac{x^2}{6^2}-\dfrac{y^2}{3^2}=1\)
8) \(5y^2 + 4x^2 = 6x\)
9) \(25x^2 - 16y^2 = 400\)
- Answer
-
yes \(\dfrac{x^2}{4^2}-\dfrac{y^2}{5^2}=1\)
10) \(-9x^2+18x+y^2+4y-14=0\)
For the exercises 11-25, write the equation for the hyperbola in standard form if it is not already, and identify the vertices and foci, and write equations of asymptotes.
11) \(\dfrac{x^2}{25}-\dfrac{y^2}{36}=1\)
- Answer
-
\(\dfrac{x^2}{5^2}-\dfrac{y^2}{6^2}=1\); vertices: \((5,0)\), \((-5,0)\); foci: \((\sqrt{61},0)\), \((-\sqrt{61},0)\); asymptotes: \(y=\dfrac{6}{5}x\), \(y=-\dfrac{6}{5}x\)
12) \(\dfrac{x^2}{100}-\dfrac{y^2}{9}=1\)
13) \(\dfrac{y^2}{4}-\dfrac{x^2}{81}=1\)
- Answer
-
\(\dfrac{y^2}{2^2}-\dfrac{x^2}{9^2}=1\); vertices: \((0,2)\), \((0,-2)\); foci: \((0,\sqrt{85})\), \((0,-\sqrt{85})\); asymptotes: \(y=\dfrac{2}{9}x\), \(y=-\dfrac{2}{9}x\)
14) \(9y^2 - 4x^2 = 1\)
15) \(\dfrac{(x-1)^2}{9}-\dfrac{(y-2)^2}{16}=1\)
- Answer
-
\(\dfrac{(x-1)^2}{3^2}-\dfrac{(y-2)^2}{4^2}=1\); vertices: \((4,2)\), \((-2,2)\); foci: \((6,2)\), \((-4,2)\); asymptotes: \(y=\dfrac{4}{3}(x-1)+2\), \(y=-\dfrac{4}{3}(x-1)+2\)
16) \(\dfrac{(y-6)^2}{36}-\dfrac{(x+1)^2}{16}=1\)
17) \(\dfrac{(x-2)^2}{49}-\dfrac{(y+7)^2}{49}=1\)
- Answer
-
\(\dfrac{(x-2)^2}{7^2}-\dfrac{(y+7)^2}{7^2}=1\); vertices: \((9,-7)\), \((-5,-7)\); foci: \((2+7\sqrt{2},-7)\), \((2-7\sqrt{2},-7)\); asymptotes: \(y=x-9\), \(y=-x-5\)
18) \(4x^2-8x-9y^2-72y+112=0\)
19) \(-9x^2-54x+9y^2-54y+81=0\)
- Answer
-
\(\dfrac{(x+3)^2}{3^2}-\dfrac{(y-3)^2}{3^2}=1\); vertices: \((0,3)\), \((-6,3)\); foci: \((-3+3\sqrt{2},1)\), \((-3-3\sqrt{2},1)\); asymptotes: \(y=x+6\), \(y=-x\)
20) \(4x^2-24x-36y^2-360y+864=0\)
21) \(-4x^2+24x+16y^2-128y+156=0\)
- Answer
-
\(\dfrac{(y-4)^2}{2^2}-\dfrac{(x-3)^2}{4^2}=1\); vertices: \((3,6)\), \((3,2)\); foci: \((3,4+2\sqrt{5})\), \((3,4-2\sqrt{5})\); asymptotes: \(y=\dfrac{1}{2}(x-3)+4\), \(y=-\dfrac{1}{2}(x-3)+4\)
22) \(-4x^2+40x+25y^2-100y+100=0\)
23) \(x^2+2x-100y^2-1000y+2401=0\)
- Answer
-
\(\dfrac{(y+5)^2}{7^2}-\dfrac{(x+1)^2}{70^2}=1\); vertices: \((-1,2)\), \((-1,-12)\); foci: \((-1,-5+7\sqrt{101})\), \((-1,-5-7\sqrt{101})\); asymptotes: \(y=\dfrac{1}{10}(x+1)-5\), \(y=-\dfrac{1}{10}(x+1)-5\)
24) \(-9x^2+72x+16y^2+16y+4=0\)
25) \(4x^2+24x-25y^2+200y-464=0\)
- Answer
-
\(\dfrac{(x+3)^2}{5^2}-\dfrac{(y-4)^2}{2^2}=1\); vertices: \((2,4)\), \((-8,4)\); foci: \((-3+\sqrt{29},4)\), \((-3-\sqrt{29},4)\); asymptotes: \(y=\dfrac{2}{5}(x+3)+4\), \(y=-\dfrac{2}{5}(x+3)+4\)
For the exercises 26-30, find the equations of the asymptotes for each hyperbola.
26) \(\dfrac{y^2}{3^2}-\dfrac{x^2}{3^2}=1\)
27) \(\dfrac{(x-3)^2}{5^2}-\dfrac{(y+4)^2}{2^2}=1\)
- Answer
-
\(y=\dfrac{2}{5}(x-3)-4\), \(y=-\dfrac{2}{5}(x-3)-4\)
28) \(\dfrac{(y-3)^2}{3^2}-\dfrac{(x+5)^2}{6^2}=1\)
29) \(9x^2-18x-16y^2+32y-151=0\)
- Answer
-
\(y=\dfrac{3}{4}(x-1)+1\), \(y=-\dfrac{3}{4}(x-1)+1\)
30) \(16y^2+96y-4x^2+16x+112=0\)
Graphical
For the exercises 31-44, sketch a graph of the hyperbola, labeling vertices and foci.
31) \(\dfrac{x^2}{49}-\dfrac{y^2}{16}=1\)
- Answer
-
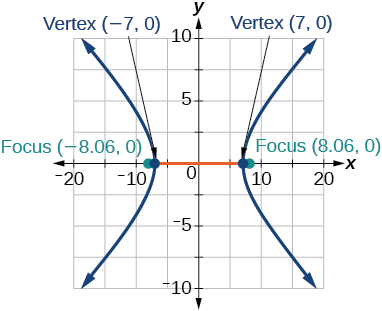
32) \(\dfrac{x^2}{64}-\dfrac{y^2}{4}=1\)
33) \(\dfrac{y^2}{9}-\dfrac{x^2}{25}=1\)
- Answer
-
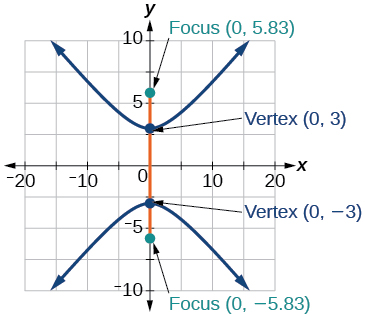
34) \(81x^2-9y^2=1\)
35) \(\dfrac{(y+5)^2}{9}-\dfrac{(x-4)^2}{25}=1\)
- Answer
-
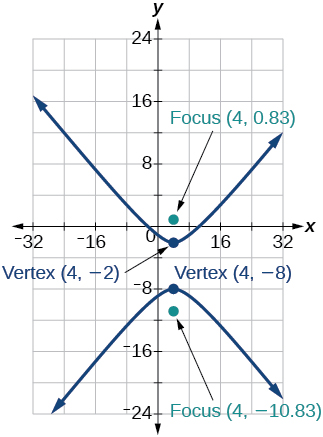
36) \(\dfrac{(x-2)^2}{8}-\dfrac{(y+3)^2}{27}=1\)
37) \(\dfrac{(y-3)^2}{9}-\dfrac{(x-3)^2}{9}=1\)
- Answer
-
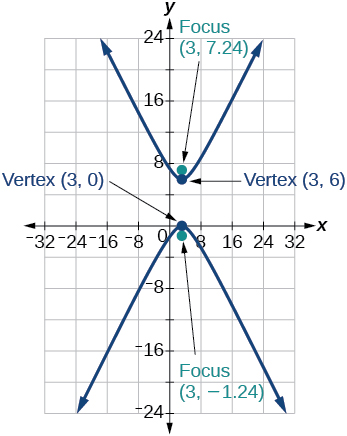
38) \(-4x^2-8x+16y^2-32y-52=0\)
39) \(x^2-8x-25y^2-100y-109=0\)
- Answer
-
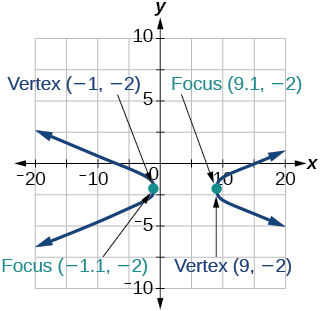
40) \(-x^2+8x+4y^2-40y+88=0\)
41) \(64x^2+128x-9y^2-72y-656=0\)
- Answer
-
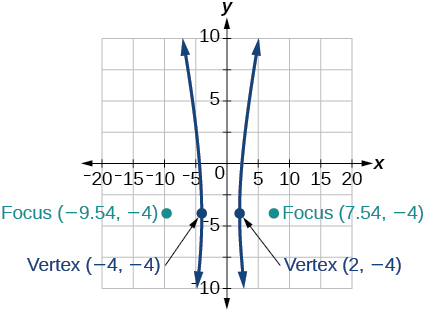
42) \(16x^2+64x-4y^2-8y-4=0\)
43) \(-100x^2+1000x+y^2-10y-2575=0\)
- Answer
-
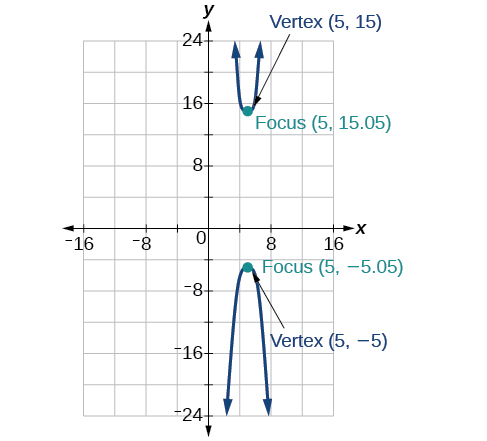
44) \(4x^2+16x-4y^2+16y+16=0\)
For the exercises 45-50, given information about the graph of the hyperbola, find its equation.
45) Vertices at \((3,0)\) and \((-3,0)\) and one focus at \((5,0)\).
- Answer
-
\(\dfrac{x^2}{9}-\dfrac{y^2}{16}=1\)
46) Vertices at \((0,6)\) and \((0,-6)\) and one focus at \((0,-8)\).
47) Vertices at \((1,1)\) and \((11,1)\) and one focus at \((12,1)\).
- Answer
-
\(\dfrac{(x-6)^2}{25}-\dfrac{(y-1)^2}{11}=1\)
48) Center: \((0,0)\); vertex: \((0,-13)\)
49) Center: \((4,2)\); vertex: \((9,2)\)
- Answer
-
\(\dfrac{(x-4)^2}{25}-\dfrac{(y-2)^2}{1}=1\)
50) Center: \((3,5)\); vertex: \((3,11)\) ; one focus: \((3,5+2\sqrt{10})\).
For the exercises 51-,55 given the graph of the hyperbola, find its equation.
51)
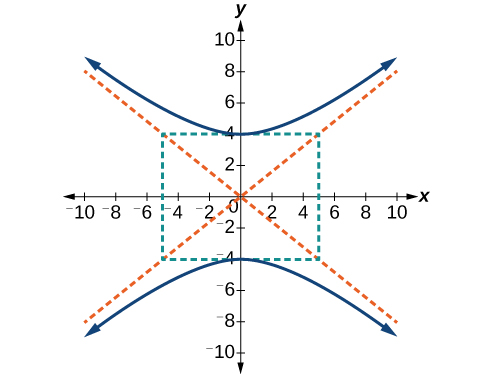
- Answer
-
\(\dfrac{y^2}{16}-\dfrac{x^2}{25}=1\)
52)
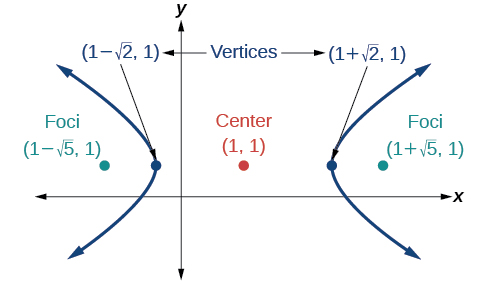
53)
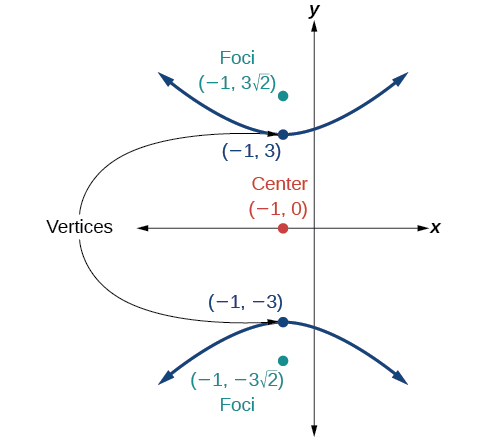
- Answer
-
\(\dfrac{y^2}{9}-\dfrac{(x+1)^2}{9}=1\)
54)
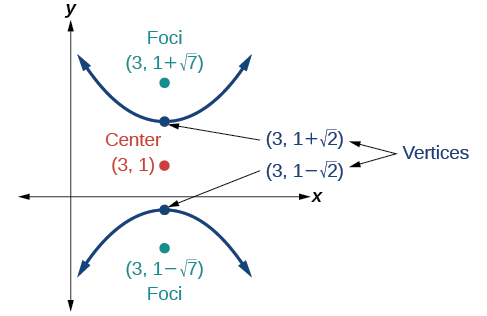
55)
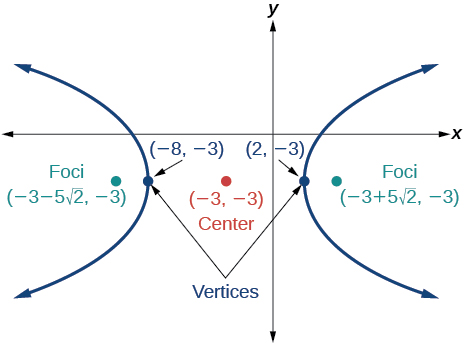
- Answer
-
\(\dfrac{(x+3)^2}{25}-\dfrac{(y+3)^2}{25}=1\)
Extensions
For the exercises 56-60, express the equation for the hyperbola as two functions, with \(y\) as a function of \(x\). Express as simply as possible. Use a graphing calculator to sketch the graph of the two functions on the same axes.
56) \(\dfrac{x^2}{4}-\dfrac{y^2}{9}=1\)
57) \(\dfrac{y^2}{9}-\dfrac{x^2}{1}=1\)
- Answer
-
\(y(x)=3\sqrt{x^2 +1}\), \(y(x)=-3\sqrt{x^2 +1}\)
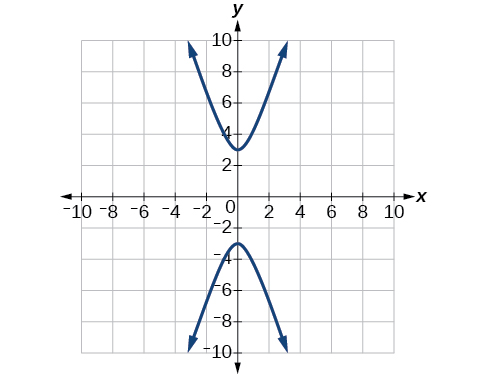
58) \(\dfrac{(x-2)^2}{16}-\dfrac{(y+3)^2}{25}=1\)
59) \(-4x^2-16x+y^2-2y-19=0\)
- Answer
-
\(y(x)=1+2\sqrt{x^2 +4x+5}\), \(y(x)=1-2\sqrt{x^2 +4x+5}\)
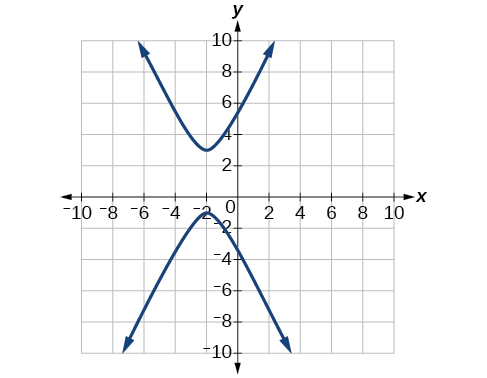
60) \(4x^2-24x-y^2-4y+16=0\)
Real-World Applications
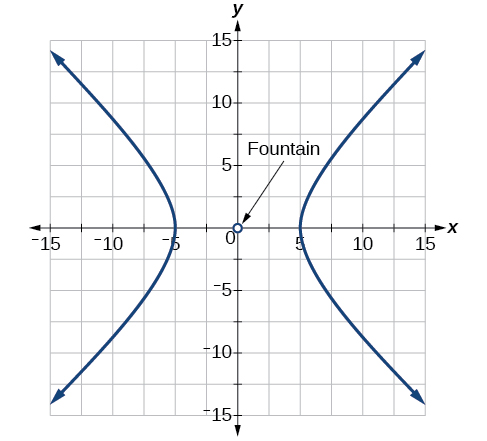
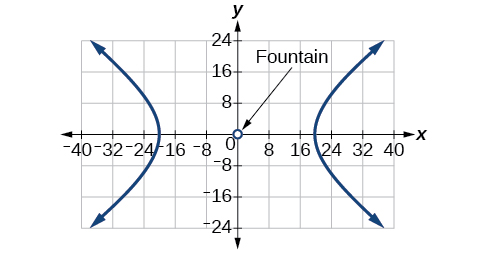
For the exercises 61-65, a hedge is to be constructed in the shape of a hyperbola near a fountain at the center of the yard. Find the equation of the hyperbola and sketch the graph.
61) The hedge will follow the asymptotes \(y=x\) and \(y=-x\), and its closest distance to the center fountain is \(5\) yards.
- Answer
-
\(\dfrac{x^2}{25}-\dfrac{y^2}{25}=1\)
62) The hedge will follow the asymptotes \(y=2x\) and \(y=-2x\), and its closest distance to the center fountain is \(6\) yards.
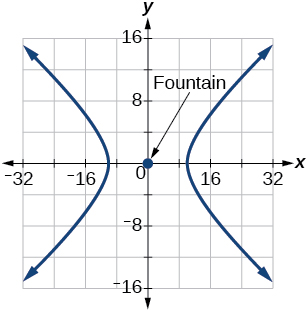
63) The hedge will follow the asymptotes \(y=\dfrac{1}{2}x\) and \(y=-\dfrac{1}{2}x\), and its closest distance to the center fountain is \(10\) yards.
- Answer
-
\(\dfrac{x^2}{100}-\dfrac{y^2}{25}=1\)
64) The hedge will follow the asymptotes \(y=\dfrac{2}{3}x\) and \(y=-\dfrac{2}{3}x\), and its closest distance to the center fountain is \(12\) yards.
65) The hedge will follow the asymptotes \(y=\dfrac{3}{4}x\) and \(y=-\dfrac{3}{4}x\), and its closest distance to the center fountain is \(20\) yards.
- Answer
-
\(\dfrac{x^2}{400}-\dfrac{y^2}{225}=1\)
For the exercises 66-70, assume an object enters our solar system and we want to graph its path on a coordinate system with the sun at the origin and the \(x\)-axis as the axis of symmetry for the object's path. Give the equation of the flight path of each object using the given information.
66) The object enters along a path approximated by the line \(y=x-2\) and passes within \(1\) au (astronomical unit) of the sun at its closest approach, so that the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line \(y=−x+2\).
67) The object enters along a path approximated by the line \(y=2x-2\) and passes within \(0.5\) au of the sun at its closest approach, so the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line \(y=-2x+2\).
- Answer
-
\(\dfrac{(x-1)^2}{0.25}-\dfrac{y^2}{0.75}=1\)
68) The object enters along a path approximated by the line \(y=0.5x+2\) and passes within \(1\) au of the sun at its closest approach, so the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line \(y=−0.5x−2\).
69) The object enters along a path approximated by the line \(y=\dfrac{1}{3}x-1\) and passes within \(1\) au of the sun at its closest approach, so the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line \(y=-\dfrac{1}{3}x+1\).
- Answer
-
\((x-3)^2 - 9y^2 = 4\)
70) The object enters along a path approximated by the line \(y=3x-9\) and passes within \(1\) au of the sun at its closest approach, so the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line \(y=−3x+9\).
10.3: The Parabola
Like the ellipse and hyperbola, the parabola can also be defined by a set of points in the coordinate plane. A parabola is the set of all points in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix.
Verbal
1) Define a parabola in terms of its focus and directrix.
- Answer
-
A parabola is the set of points in the plane that lie equidistant from a fixed point, the focus, and a fixed line, the directrix.
2) If the equation of a parabola is written in standard form and \(p\) is positive and the directrix is a vertical line, then what can we conclude about its graph?
3) If the equation of a parabola is written in standard form and \(p\) is negative and the directrix is a horizontal line, then what can we conclude about its graph?
- Answer
-
The graph will open down.
4) What is the effect on the graph of a parabola if its equation in standard form has increasing values of \(p\)?
5) As the graph of a parabola becomes wider, what will happen to the distance between the focus and directrix?
- Answer
-
The distance between the focus and directrix will increase.
Algebraic
For the exercises 6-10, determine whether the given equation is a parabola. If so, rewrite the equation in standard form.
6) \(y^2=4-x^2\)
7) \(y=4x^2\)
- Answer
-
yes \(y=4(1)x^2\)
8) \(3x^2-6y^2=12\)
9) \((y-3)^2=8(x-2)\)
- Answer
-
yes \((y-3)^2=4(2)(x-2)\)
10) \(y^2+12x-6y-51=0\)
For the exercises 11-30, rewrite the given equation in standard form, and then determine the vertex \((V)\), focus \((F)\), and directrix \((d)\) of the parabola.
11) \(x=8y^2\)
- Answer
-
\(y^2=\dfrac{1}{8}x\), \(V:(0,0)\), \(F:\left (\dfrac{1}{32},0 \right )\), \(d:x=-\dfrac{1}{32}\)
12) \(y=\dfrac{1}{4}x^2\)
13) \(y=-4x^2\)
- Answer
-
\(x^2=-\dfrac{1}{4}y\), \(V:(0,0)\), \(F:\left (0,-\dfrac{1}{16} \right )\), \(d:y=-\dfrac{1}{16}\)
14) \(x=\dfrac{1}{8}y^2\)
15) \(x=36y^2\)
- Answer
-
\(y^2=\dfrac{1}{36}x\), \(V:(0,0)\), \(F:\left (\dfrac{1}{144},0 \right )\), \(d:x=-\dfrac{1}{144}\)
16) \(x=\dfrac{1}{36}y^2\)
17) \((x-1)^2=4(y-1)\)
- Answer
-
\((x-1)^2=4(y-1)\), \(V:(1,1)\), \(F:(1,2)\), \(d:y=0\)
18) \((y-2)^2=\dfrac{4}{5}(x+4)\)
19) \((y-4)^2=2(x+3)\)
- Answer
-
\((y-4)^2=2(x+3)\), \(V:(-3,4)\), \(F:\left (-\dfrac{5}{2},4 \right )\), \(d:x=-\dfrac{7}{2}\)
20) \((x+1)^2=2(y+4)\)
21) \((x+4)^2=24(y+1)\)
- Answer
-
\((x+4)^2=24(y+1)\), \(V:(-4,-1)\), \(F:(-4,5)\), \(d:y=-7\)
22) \((y+4)^2=16(x+4)\)
23) \(y^2+12x-6y+21=0\)
- Answer
-
\((y-3)^2=-12(x+1)\), \(V:(-1,3)\), \(F:(-4,3)\), \(d:x=2\)
24) \(x^2-4x-24y+28=0\)
25) \(5x^2-50x-4y+113=0\)
- Answer
-
\((x-5)^2=\dfrac{4}{5}(y+3)\), \(V:(5,-3)\), \(F:\left (5,-\dfrac{14}{5} \right )\), \(d:y=-\dfrac{16}{5}\)
26) \(y^2-24x+4y-68=0\)
27) \(x^2-4x+2y-6=0\)
- Answer
-
\((x-2)^2=-2(y-5)\), \(V:(2,5)\), \(F:\left (2,\dfrac{9}{2} \right )\), \(d:y=\dfrac{11}{2}\)
28) \(y^2-6y+12x-3=0\)
29) \(3y^2-4x-6y+23=0\)
- Answer
-
\((y-1)^2=\dfrac{4}{3}(x-5)\), \(V:(5,1)\), \(F:\left (\dfrac{16}{3},1 \right )\), \(d:x=\dfrac{14}{3}\)
30) \(x^2+4x+8y-4=0\)
Graphical
For the exercises 31-44, graph the parabola, labeling the focus and the directrix.
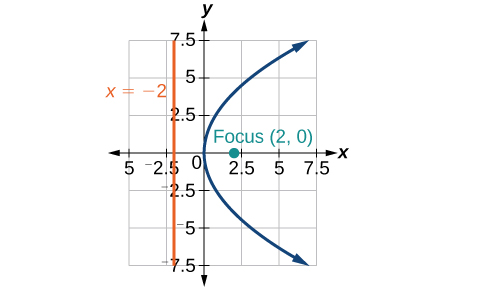
31) \(x=\dfrac{1}{8}y^2\)
- Answer
-
32) \(y=36x^2\)
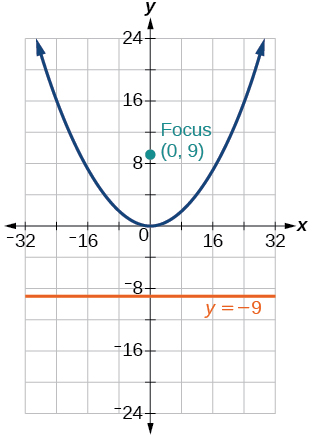
33) \(y=\dfrac{1}{36}x^2\)
- Answer
-
34) \(y=-9x^2\)
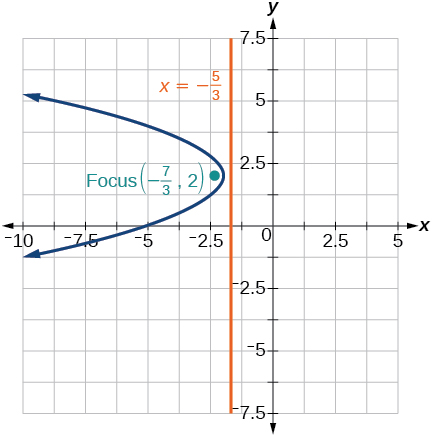
35) \((y-2)^2=-\dfrac{4}{3}(x+2)\)
- Answer
-
36) \(-5(x+5)^2=4(y+5)\)
37) \(-6(y+5)^2=4(x-4)\)
- Answer
-
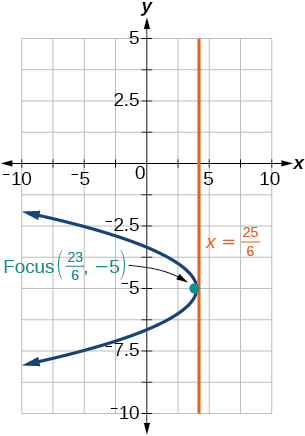
38) \(y^2-6y-8x+1=0\)
39) \(x^2+8x+4y+20=0\)
- Answer
-
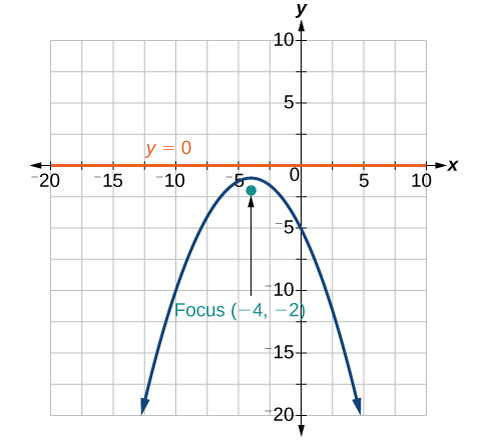
40) \(3x^2+30x-4y+95=0\)
41) \(y^2-8x+10y+9=0\)
- Answer
-
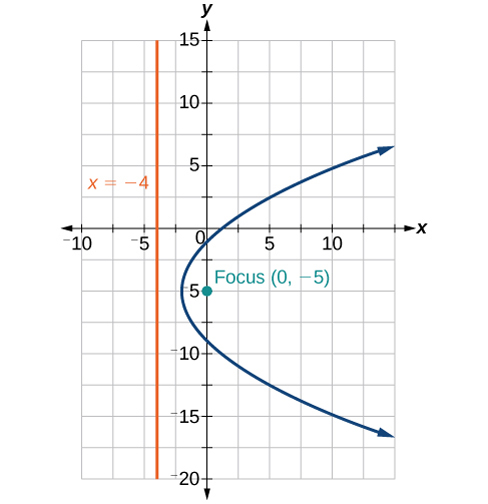
42) \(x^2+4x+2y+2=0\)
43) \(y^2+2y-12x+61=0\)
- Answer
-
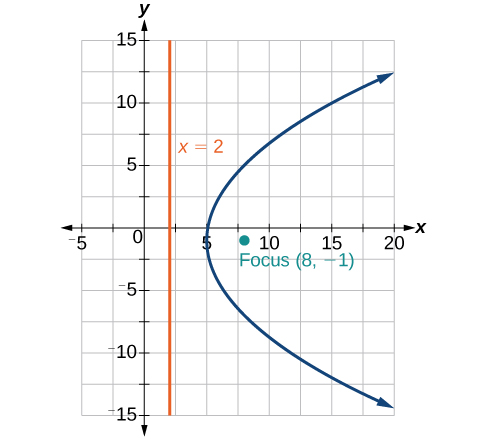
44) \(-2x^2+8x-4y-24=0\)
For the exercises 45-50, find the equation of the parabola given information about its graph.
45) Vertex is \((0,0)\); directrix is \(y=4\), focus is \((0,-4)\).
- Answer
-
\(x^2=-16y\)
46) Vertex is \((0,0)\); directrix is \(x=4\), focus is \((-4,0)\).
47) Vertex is \((2,2)\); directrix is \(x=2-\sqrt{2}\), focus is \((2+\sqrt{2},2)\).
- Answer
-
\((y-2)^2 = 4\sqrt{2}(x-2)\)
48) Vertex is \((-2,3)\); directrix is \(x=-\dfrac{7}{2}\), focus is \( \left(-\dfrac{1}{2},3 \right)\).
49) Vertex is \((\sqrt{2},-\sqrt{3})\); directrix is \(x=2\sqrt{2}\), focus is \((0,-\sqrt{3})\).
- Answer
-
\((y+\sqrt{3})^2 = -4\sqrt{2}(x-\sqrt{2})\)
50) Vertex is \((-,21)\); directrix is \(y=\dfrac{11}{3}\), focus is \( \left(1,\dfrac{1}{3} \right)\).
For the exercises 51-55, determine the equation for the parabola from its graph.
51)
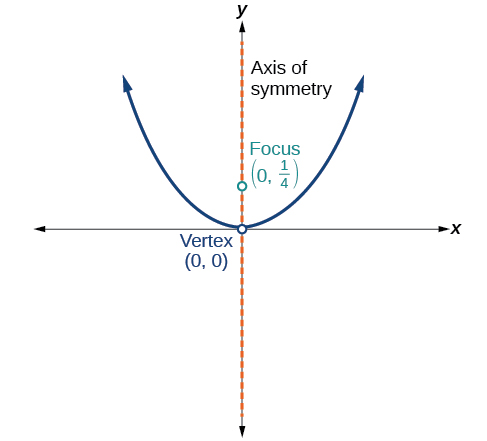
- Answer
-
\(x^2=y\)
52)
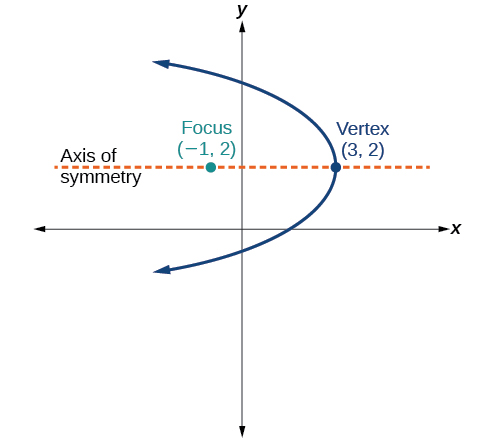
53)
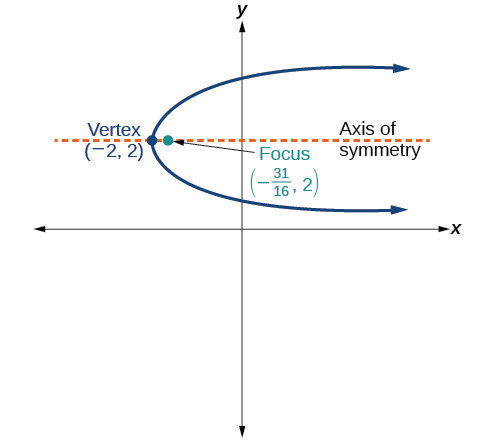
- Answer
-
\((y-2)^2 = \dfrac{1}{4}(x+2)\)
54)
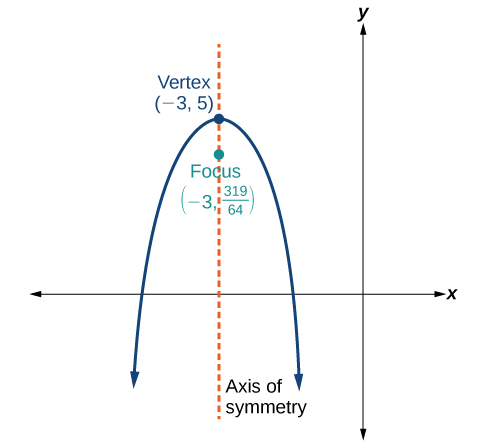
55)
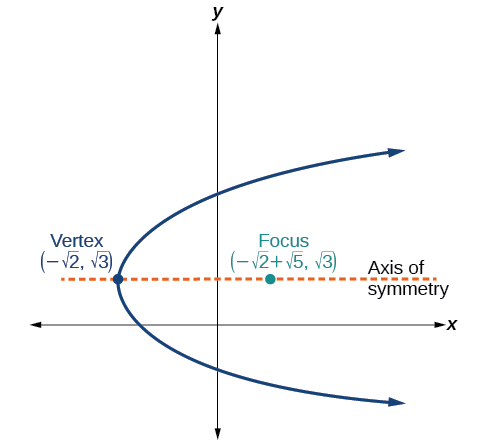
- Answer
-
\((y-\sqrt{2})^2 = 4\sqrt{5}(x+\sqrt{2})\)
Extensions
For the exercises 56-60, the vertex and endpoints of the latus rectum of a parabola are given. Find the equation.
56) \(V(0,0)\), Endpoints \((2,1),(−2,1)\)
57) \(V(0,0)\), Endpoints \((-2,4),(−2,-4)\)
- Answer
-
\(y^2=-8x\)
58) \(V(1,2)\), Endpoints \((-5,5),(7,5)\)
59) \(V(-3,-1)\), Endpoints \((0,5),(0,-7)\)
- Answer
-
\((y+1)^2 = 12(x+3)\)
60) \(V(4,-3)\), Endpoints \(\left ( 5,-\dfrac{7}{2} \right ), \left ( 3,-\dfrac{7}{2} \right )\)
Real-World Applications
61) The mirror in an automobile headlight has a parabolic cross-section with the light bulb at the focus. On a schematic, the equation of the parabola is given as \(x^2=4y\). At what coordinates should you place the light bulb?
- Answer
-
\((0,1)\)
62) If we want to construct the mirror from the previous exercise such that the focus is located at \((0,0.25)\) what should the equation of the parabola be?
63) A satellite dish is shaped like a paraboloid of revolution. This means that it can be formed by rotating a parabola around its axis of symmetry. The receiver is to be located at the focus. If the dish is \(12\) feet across at its opening and \(4\) feet deep at its center, where should the receiver be placed?
- Answer
-
At the point \(2.25\) feet above the vertex.
64) Consider the satellite dish from the previous exercise. If the dish is \(8\) feet across at the opening and \(2\) feet deep, where should we place the receiver?
65) A searchlight is shaped like a paraboloid of revolution. A light source is located \(1\) foot from the base along the axis of symmetry. If the opening of the searchlight is \(3\) feet across, find the depth.
- Answer
-
\(0.5625\) feet
66) If the searchlight from the previous exercise has the light source located \(6\) inches from the base along the axis of symmetry and the opening is \(4\) feet, find the depth.
67) An arch is in the shape of a parabola. It has a span of \(100\) feet and a maximum height of \(20\) feet. Find the equation of the parabola, and determine the height of the arch \(40\) feet from the center.
- Answer
-
\(x^2=-125(y-20)\), height is \(7.2\) feet
68) If the arch from the previous exercise has a span of \(160\) feet and a maximum height of \(40\) feet, find the equation of the parabola, and determine the distance from the center at which the height is \(20\) feet.
69) An object is projected so as to follow a parabolic path given by \(y=-x^2+96x\) where \(x\) is the horizontal distance traveled in feet and \(y\) is the height. Determine the maximum height the object reaches.
- Answer
-
\(2304\) feet
70) For the object from the previous exercise, assume the path followed is given by \(y=-0.5x^2+80x\). Determine how far along the horizontal the object traveled to reach maximum height.
10.4: Rotation of Axes
In previous sections of this chapter, we have focused on the standard form equations for nondegenerate conic sections. In this section, we will shift our focus to the general form equation, which can be used for any conic. The general form is set equal to zero, and the terms and coefficients are given in a particular order, as shown below.
Verbal
1) What effect does the \(xy\) term have on the graph of a conic section?
- Answer
-
The \(xy\) term causes a rotation of the graph to occur.
2) If the equation of a conic section is written in the form \(Ax^2+By^2+Cx+Dy+E=0\) and \(AB=0\) what can we conclude?
3) If the equation of a conic section is written in the form \(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\), and \(B^2-4AC>0\), what can we conclude?
- Answer
-
The conic section is a hyperbola.
4) Given the equation \(ax^2+4x+3y^2-12=0\), what can we conclude if \(a>0\)?
5) For the equation \(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) the value of \(\theta \) that satisfies \(\cot (2\theta )=\dfrac{A-C}{B}\) gives us what information?
- Answer
-
It gives the angle of rotation of the axes in order to eliminate the \(xy\) term.
Algebraic
For the exercises 6-17, determine which conic section is represented based on the given equation.
6) \(9x^2+4y^2+72x+36y-500=0\)
7) \(x^2-10x+4y-10=0\)
- Answer
-
\(AB=0\), parabola
8) \(2x^2-2y^2+4x-6y-2=0\)
9) \(4x^2-y^2+8x-1=0\)
- Answer
-
\(AB=-4<0\), hyperbola
10) \(4y^2-5x+9y+1=0\)
11) \(2x^2+3y^2-8x-12y+2=0\)
- Answer
-
\(AB=6>0\), ellipse
12) \(4x^2+9xy+4y^2-36y-125=0\)
13) \(3x^2+6xy+3y^2-36y-125=0\)
- Answer
-
\(B^2 - 4AC=0\), parabola
14) \(-3x^2+3\sqrt{3}xy-4y^2+9=0\)
15) \(2x^2+4\sqrt{3}xy+6y^2-6x-3=0\)
- Answer
-
\(B^2 - 4AC=0\), parabola
16) \(-x^2+4\sqrt{2}xy+2y^2-2y+1=0\)
17) \(8x^2+4\sqrt{2}xy+4y^2-10x+1=0\)
- Answer
-
\(B^2 - 4AC=-96<0\), ellipse
For the exercises 18-22, find a new representation of the given equation after rotating through the given angle.
18) \(3x^2+xy+3y^2-5=0, \theta =45^{\circ}\)
19) \(4x^2-xy+4y^2-2=0, \theta =45^{\circ}\)
- Answer
-
\(7x'^2+9y'^2-4=0\)
20) \(2x^2+8xy-1=0, \theta =30^{\circ}\)
21) \(-2x^2+8xy+1=0, \theta =45^{\circ}\)
- Answer
-
\(3x'^2+2x'y'-5y'^2+1=0\)
22) \(4x^2+\sqrt{2}xy+4y^2+y+2=0, \theta =45^{\circ}\)
For the exercises 23-30, determine the angle \(\theta \) that will eliminate the \(xy\) term and write the corresponding equation without the \(xy\) term.
23) \(x^2+3\sqrt{3}xy+4y^2+y-2=0\)
- Answer
-
\(\theta =60^{\circ},11x'^2-y'2+\sqrt{3}x'+y'-4=0\)
24) \(4x^2+2\sqrt{3}xy+6y^2+y-2=0\)
25) \(9x^2-3\sqrt{3}xy+6y^2+4y-3=0\)
- Answer
-
\(\theta =150^{\circ},21x'^2+9y'^2+4x'-4\sqrt{3}y'-6=0\)
26) \(-3x^2-\sqrt{3}xy-2y^2-x=0\)
27) \(16x^2+24xy+9y^2+6x-6y+2=0\)
- Answer
-
\(\theta \approx 36.9^{\circ},125x'^2+6x'-42y'+10=0\)
28) \(x^2+4xy+4y^2+3x-2=0\)
29) \(x^2+4xy+y^2-2x+1=0\)
- Answer
-
\(\theta =45^{\circ},3x'^2-y'^2-\sqrt{2}x'+\sqrt{2}y'+1=0\)
30) \(4x^2-2\sqrt{3}xy+6y^2-1=0\)
Graphical
For the exercises 31-38, rotate through the given angle based on the given equation. Give the new equation and graph the original and rotated equation.
31) \(y=-x^2,\theta =-45^{\circ}\)
- Answer
-
\(\dfrac{\sqrt{2}}{2}(x'+y')=\dfrac{1}{2}(x'-y')^2\)
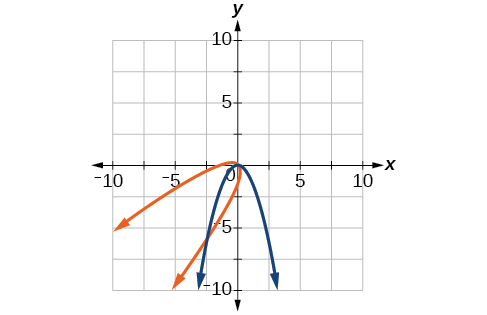
32) \(x=y^2,\theta =45^{\circ}\)
33) \(\dfrac{x^2}{4}+\dfrac{y^2}{1}=1,\theta =45^{\circ}\)
- Answer
-
\(\dfrac{(x'-y')^2}{8}+\dfrac{(x'+y')^2}{2}=1\)
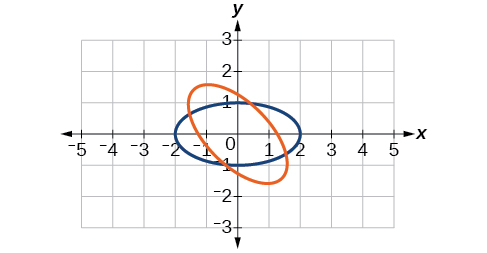
34) \(\dfrac{y^2}{16}+\dfrac{x^2}{9}=1,\theta =45^{\circ}\)
35) \(y^2 - x^2 = 1, \theta =45^{\circ}\)
- Answer
-
\(\dfrac{(x'+y')^2}{2}-\dfrac{(x'-y')^2}{2}=1\)
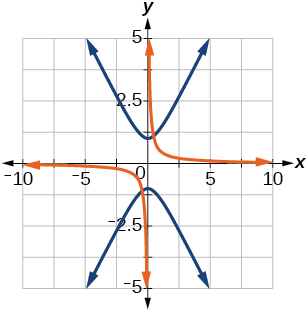
36) \(y=\dfrac{x^2}{2}, \theta =30^{\circ}\)
37) \(x=(y-1)^2, \theta =30^{\circ}\)
- Answer
-
\(\dfrac{\sqrt{3}}{2}x'-\dfrac{1}{2}y'=\left ( \dfrac{1}{2}x' + \dfrac{\sqrt{3}}{2}x' - 1 \right )^2\)
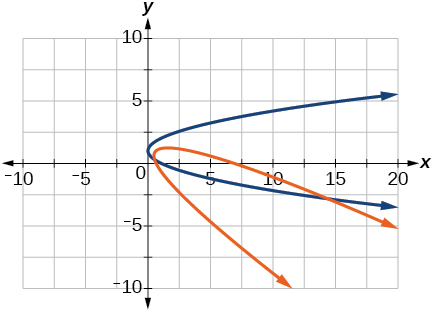
38) \(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1,\theta =30^{\circ}\)
For the exercises 39-49, graph the equation relative to the \(x'y'\) system in which the equation has no \(x'y'\) term.
39) \(xy=9\)
- Answer
-
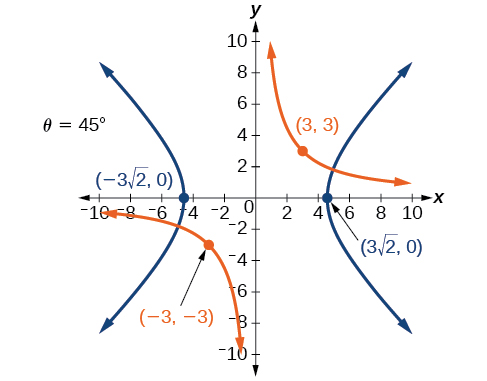
40) \(x^2+10xy+y^2-6=0\)
41) \(x^2-10xy+y^2-24=0\)
- Answer
-
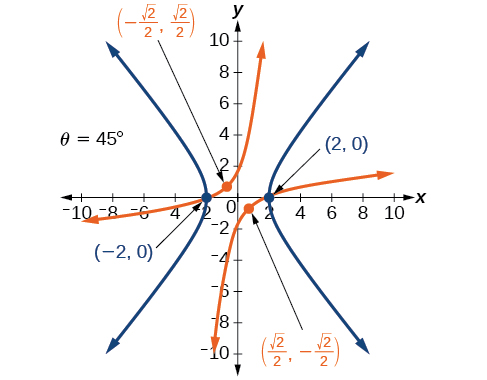
42) \(4x^2-3\sqrt{3}xy+y^2-22=0\)
43) \(6x^2+2\sqrt{3}xy+4y^2-21=0\)
- Answer
-
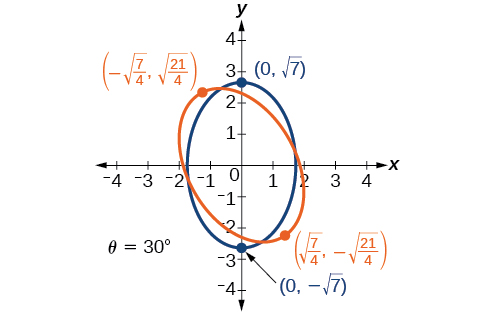
44) \(11x^2+10\sqrt{3}xy+y^2-64=0\)
45) \(21x^2+2\sqrt{3}xy+19y^2-18=0\)
- Answer
-
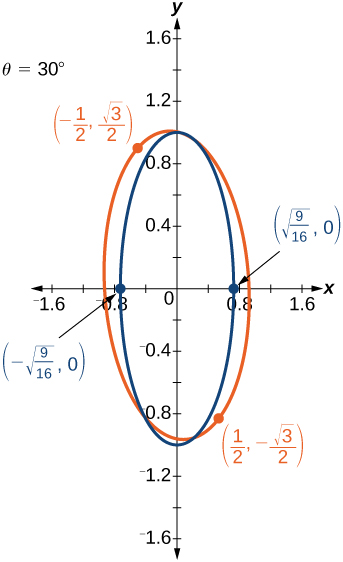
46) \(16x^2+24xy+9y^2-130x+90y=0\)
47) \(16x^2+24xy+9y^2-60x+80y=0\)
- Answer
-
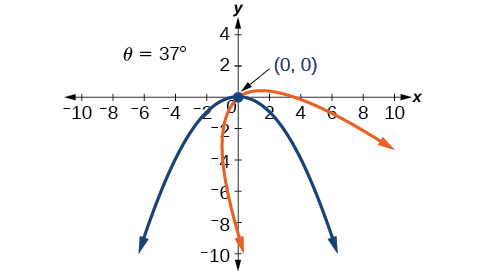
48) \(13x^2-6\sqrt{3}xy+7y^2-16=0\)
49) \(4x^2-4xy+y^2-8\sqrt{5}x-16\sqrt{5}y=0\)
- Answer
-
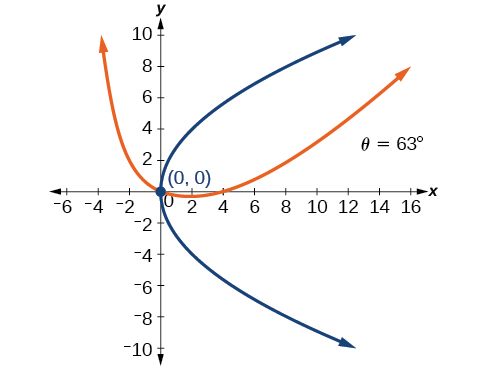
For the exercises 50-55, determine the angle of rotation in order to eliminate the \(xy\) term. Then graph the new set of axes.
50) \(6x^2-5\sqrt{3}xy+y^2+10x-12y=0\)
51) \(6x^2-5xy+6y^2+20x-y=0\)
- Answer
-
\(\theta =45^{\circ}\)
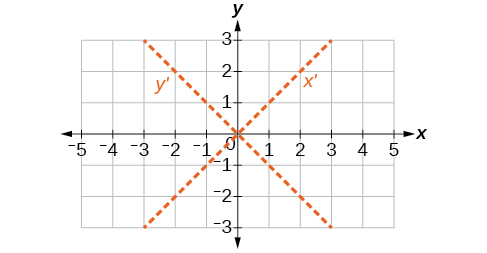
52) \(6x^2-8\sqrt{3}xy+14y^2+10x-3y=0\)
53) \(4x^2+6\sqrt{3}xy+10y^2+20x-40y=0\)
- Answer
-
\(\theta =60^{\circ}\)
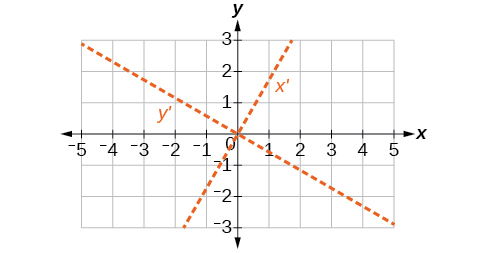
54) \(8x^2+3xy+4y^2+2x-4=0\)
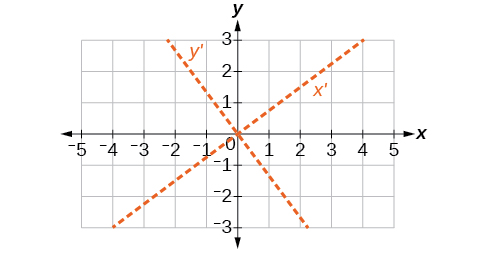
55) \(16x^2+24xy+9y^2+20x-44y=0\)
- Answer
-
\(\theta \approx 36.9^{\circ}\)
For the exercises 56-60, determine the value of \(k\) based on the given equation.
56) Given \(4x^2+kxy+16y^2+8x+24y-48=0\), find \(k\) for the graph to be a parabola.
57) Given \(2x^2+kxy+12y^2+10x-16y+28=0\), find \(k\) for the graph to be an ellipse.
- Answer
-
\(-4\sqrt{6}<k<4\sqrt{6}\)
58) Given \(3x^2+kxy+4y^2-6x+20y+128=0\), find \(k\) for the graph to be a hyperbola.
59) Given \(kx^2+8xy+8y^2-12x+16y+18=0\) find \(k\) for the graph to be a parabola.
- Answer
-
\(k=2\)
60) Given \(6x^2+12xy+ky^2+16x+10y+4=0\) find \(k\) for the graph to be an ellipse.
10.5: Conic Sections in Polar Coordinates
In this section, we will learn how to define any conic in the polar coordinate system in terms of a fixed point, the focus at the pole, and a line, the directrix, which is perpendicular to the polar axis.
Verbal
1) Explain how eccentricity determines which conic section is given.
- Answer
-
If eccentricity is less than \(1\), it is an ellipse. If eccentricity is equal to \(1\), it is a parabola. If eccentricity is greater than \(1\), it is a hyperbola.
2) If a conic section is written as a polar equation, what must be true of the denominator?
3) If a conic section is written as a polar equation, and the denominator involves \(\sin \theta \) what conclusion can be drawn about the directrix?
- Answer
-
The directrix will be parallel to the polar axis.
4) If the directrix of a conic section is perpendicular to the polar axis, what do we know about the equation of the graph?
5) What do we know about the focus/foci of a conic section if it is written as a polar equation?
- Answer
-
One of the foci will be located at the origin.
Algebraic
For the exercises 6-17, identify the conic with a focus at the origin, and then give the directrix and eccentricity.
6) \(r=\dfrac{6}{1-2\cos \theta }\)
7) \(r=\dfrac{3}{4-4\sin \theta }\)
- Answer
-
Parabola with \(e=1\) and directrix \(\dfrac{3}{4}\) units below the pole.
8) \(r=\dfrac{8}{4-3\cos \theta }\)
9) \(r=\dfrac{5}{1+2\sin \theta }\)
- Answer
-
Hyperbola with \(e=2\) and directrix \(\dfrac{5}{2}\) units above the pole.
10) \(r=\dfrac{15}{4+3\cos \theta }\)
11) \(r=\dfrac{3}{10+10\cos \theta }\)
- Answer
-
Parabola with \(e=1\) and directrix \(\dfrac{3}{10}\) units to the right of the pole.
12) \(r=\dfrac{2}{1-\cos \theta }\)
13) \(r=\dfrac{4}{7+2\cos \theta }\)
- Answer
-
Ellipse with \(e=\dfrac{2}{7}\) and directrix \(2\) units to the right of the pole.
14) \(r(1-\cos \theta )=3\)
15) \(r(3+5\sin \theta )=11\)
- Answer
-
Hyperbola with \(e=\dfrac{5}{3}\) and directrix \(\dfrac{11}{5}\) units above the pole.
16) \(r(4-5\sin \theta )=1\)
17) \(r(7+8\sin \theta )=7\)
- Answer
-
Hyperbola with \(e=\dfrac{8}{7}\) and directrix \(\dfrac{7}{8}\) units to the right of the pole.
For the exercises 18-30, convert the polar equation of a conic section to a rectangular equation.
18) \(r=\dfrac{4}{1+3\sin \theta }\)
19) \(r=\dfrac{2}{5-3\sin \theta }\)
- Answer
-
\(25x^2+16y^2-12y-4=0\)
20) \(r=\dfrac{8}{3-2\cos \theta }\)
21) \(r=\dfrac{3}{2+5\cos \theta }\)
- Answer
-
\(21x^2-4y^2-30x+9=0\)
22) \(r=\dfrac{4}{2+2\sin \theta }\)
23) \(r=\dfrac{3}{8-8\cos \theta }\)
- Answer
-
\(64y^2=48x+9\)
24) \(r=\dfrac{2}{6+7\cos \theta }\)
25) \(r=\dfrac{5}{5-11\sin \theta }\)
- Answer
-
\(96y^2-25x^2+110y+25=0\)
26) \(r(5+2\cos \theta )=6\)
27) \(r(2-\cos \theta )=1\)
- Answer
-
\(3x^2+4y^2-2x-1=0\)
28) \(r(2.5-2.5\sin \theta )=5\)
29) \(r=\dfrac{6\sec \theta }{-2+3\sec \theta }\)
- Answer
-
\(5x^2+9y^2-24x-36=0\)
30) \(r=\dfrac{6\csc \theta }{3+2\csc \theta }\)
For the exercises 31-42, graph the given conic section. If it is a parabola, label the vertex, focus, and directrix. If it is an ellipse, label the vertices and foci. If it is a hyperbola, label the vertices and foci.
31) \(r=\dfrac{5}{2+\cos \theta }\)
- Answer
-

32) \(r=\dfrac{2}{3+3\sin \theta }\)
33) \(r=\dfrac{10}{5-4\sin \theta }\)
- Answer
-
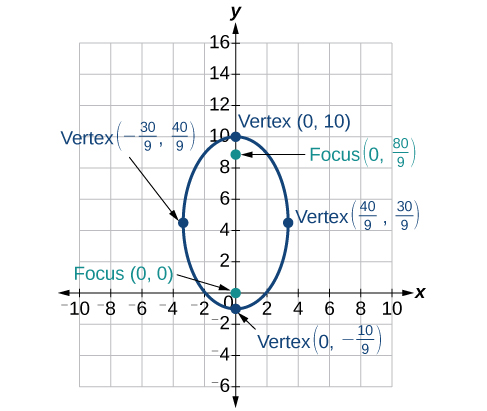
34) \(r=\dfrac{3}{1+2\cos \theta }\)
35) \(r=\dfrac{8}{4-5\cos \theta }\)
- Answer
-
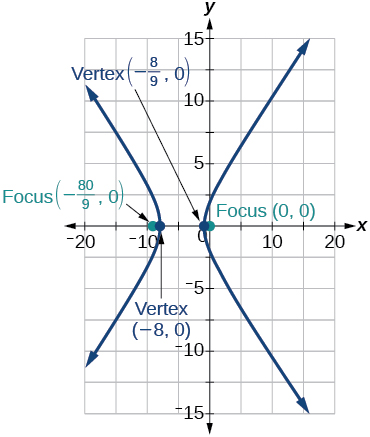
36) \(r=\dfrac{3}{4-4\cos \theta }\)
37) \(r=\dfrac{2}{1-\sin \theta }\)
- Answer
-
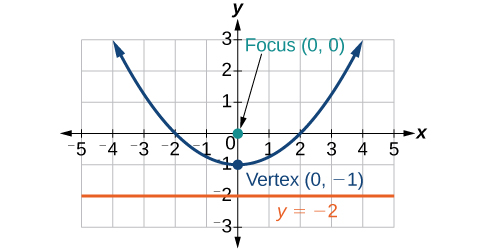
38) \(r=\dfrac{6}{3+2\sin \theta }\)
39) \(r(1+\cos \theta )=5\)
- Answer
-
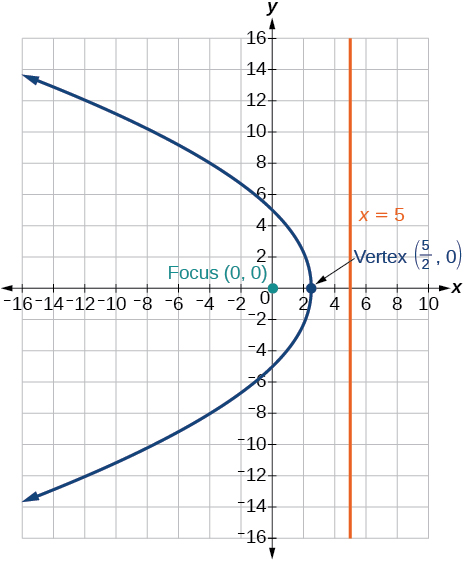
40) \(r(3-4\sin \theta )=9\)
41) \(r(3-2\sin \theta )=6\)
- Answer
-
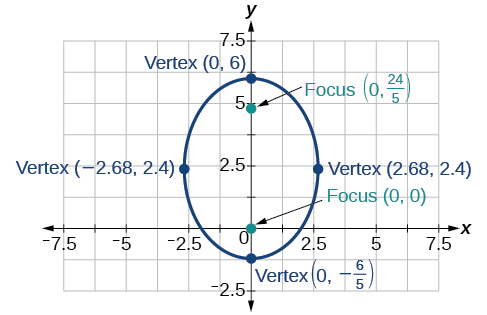
42) \(r(4-6\cos \theta )=5\)
For the exercises 43-, find the polar equation of the conic with focus at the origin and the given eccentricity and directrix.
43) Directrix: \(x=4\); \(e=\dfrac{1}{5}\)
- Answer
-
\(r=\dfrac{4}{5+\cos \theta }\)
44) Directrix: \(x=-4\); \(e=5\)
45) Directrix: \(y=2\); \(e=2\)
- Answer
-
\(r=\dfrac{4}{1+2\sin \theta }\)
46) Directrix: \(y=-2\); \(e=\dfrac{1}{2}\)
47) Directrix: \(x=1\); \(e=1\)
- Answer
-
\(r=\dfrac{1}{1+\cos \theta }\)
48) Directrix: \(x=-1\); \(e=1\)
49) Directrix: \(x=-\dfrac{1}{4}\); \(e=\dfrac{7}{2}\)
- Answer
-
\(r=\dfrac{7}{8-28\cos \theta }\)
50) Directrix: \(y=-\dfrac{2}{5}\); \(e=\dfrac{7}{2}\)
51) Directrix: \(y=4\); \(e=\dfrac{3}{2}\)
- Answer
-
\(r=\dfrac{12}{2+3\sin \theta }\)
52) Directrix: \(x=-2\); \(e=\dfrac{8}{3}\)
53) Directrix: \(x=-5\); \(e=\dfrac{3}{4}\)
- Answer
-
\(r=\dfrac{15}{4-3\cos \theta }\)
54) Directrix: \(y=2\); \(e=2.5\)
55) Directrix: \(x=-3\); \(e=\dfrac{1}{3}\)
- Answer
-
\(r=\dfrac{3}{3-3\cos \theta }\)
Extensions
Recall from Rotation of Axes that equations of conics with an \(xy\) term have rotated graphs. For the following exercises, express each equation in polar form with \(r\) as a function of \(\theta \).
56) \(xy=2\)
57) \(x^2+xy+y^2=4\)
- Answer
-
\(r=\pm \dfrac{2}{\sqrt{1+\sin \theta \cos \theta }}\)
58) \(2x^2+4xy+2y^2=9\)
59) \(16x^2+24xy+9y^2=4\)
- Answer
-
\(r=\pm \dfrac{2}{4\cos \theta +3\sin \theta }\)
60) \(2xy+y=1\)
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


