1.4: Function Notation

In Definition 1.6, we described a function as a special kind of relation \(-\) one in which each \(x\)-coordinate is matched with only one \(y\)-coordinate. In this section, we focus more on the process by which the \(x\) is matched with the \(y\). If we think of the domain of a function as a set of inputs and the range as a set of outputs, we can think of a function \(f\) as a process by which each input \(x\) is matched with only one output \(y\). Since the output is completely determined by the input \(x\) and the process \(f\), we symbolize the output with function notation: ‘\(f(x)\)’, read ‘\(f\) of \(x\).’ In other words, \(f(x)\) is the output which results by applying the process \(f\) to the input \(x\). In this case, the parentheses here do not indicate multiplication, as they do elsewhere in Algebra. This can cause confusion if the context is not clear, so you must read carefully. This relationship is typically visualized using a diagram similar to the one below.

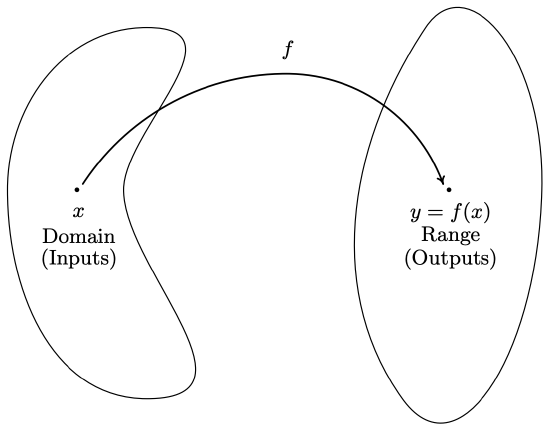
The value of \(y\) is completely dependent on the choice of \(x\). For this reason, \(x\) is often called the independent variable, or argument of \(f\), whereas \(y\) is often called the dependent variable. [functionargument]

As we shall see, the process of a function \(f\) is usually described using an algebraic formula. For example, suppose a function \(f\) takes a real number and performs the following two steps, in sequence

1. multiply by 3
2. add 4

If we choose \(5\) as our input, in step 1 we multiply by \(3\) to get \((5)(3) = 15\). In step 2, we add 4 to our result from step 1 which yields \(15 + 4 = 19\). Using function notation, we would write \(f(5) = 19\) to indicate that the result of applying the process \(f\) to the input \(5\) gives the output \(19\). In general, if we use \(x\) for the input, applying step 1 produces \(3x\). Following with step 2 produces \(3x+4\) as our final output. Hence for an input \(x\), we get the output \(f(x) = 3x + 4\). Notice that to check our formula for the case \(x=5\), we replace the occurrence of \(x\) in the formula for \(f(x)\) with \(5\) to get \(f(5) = 3(5) + 4 = 15 + 4 = 19\), as required.

Example 1.4.1

Suppose a function \(g\) is described by applying the following steps, in sequence

1. add 4
2. multiply by 3

Determine \(g(5)\) and find an expression for \(g(x)\).

Solution

Starting with \(5\), step 1 gives \(5+4 = 9\). Continuing with step 2, we get \((3)(9) = 27\). To find a formula for \(g(x)\), we start with our input \(x\). Step 1 produces \(x+4\). We now wish to multiply this entire quantity by \(3\), so we use a parentheses: \(3(x+4) = 3x + 12\). Hence, \(g(x) = 3x + 12\). We can check our formula by replacing \(x\) with \(5\) to get \(g(5) = 3(5) + 12 = 15 + 12 = 27 \, \checkmark\).

Most of the functions we will encounter in College Algebra will be described using formulas like the ones we developed for \(f(x)\) and \(g(x)\) above. Evaluating formulas using this function notation is a key skill for success in this and many other Math courses.

Example 1.4.2

Let \(f(x) = -x^2 + 3x + 4\)

1. Find and simplify the following.
   1. \(f(-1)\), \(f(0)\), \(f(2)\)
   2. \(f(2x)\), \(2 f(x)\)
   3. \(f(x+2)\), \(f(x)+2\), \(f(x) + f(2)\)
2. Solve \(f(x) = 4\).

Solution.

1. 1. To find \(f(-1)\), we replace every occurrence of \(x\) in the expression \(f(x)\) with \(-1\)

      \(\begin{array}{rclr} f(-1) & = & -(-1)^2 + 3(-1) + 4 & \\ & = & -(1) + (-3) + 4 & \\ & = & 0 & \\ \end{array}\)

      Similarly, \(f(0) = -(0)^2 + 3(0) + 4 = 4\), and \(f(2) = -(2)^2 + 3(2) + 4 = -4+6+4 = 6\).

   2. To find \(f(2x)\), we replace every occurrence of \(x\) with the quantity \(2x\)

      \(\begin{array}{rclr} f(2x) & = & -(2x)^2 + 3(2x) + 4 & \\ & = & -(4x^2) + (6x) + 4 & \\ & = & -4x^2+6x+4 & \\ \end{array}\)

      The expression \(2f(x)\) means we multiply the expression \(f(x)\) by \(2\)

      \(\begin{array}{rclr} 2f(x) & = & 2\left(-x^2 + 3x + 4\right) & \\ & = & -2x^2 + 6x + 8 \\ \end{array}\)

   3. To find \(f(x+2)\), we replace every occurrence of \(x\) with the quantity \(x+2\)

      \(\begin{array}{rclr} f(x+2) & = & -(x+2)^2 + 3(x+2) + 4 & \\ & = & -\left(x^2 + 4x + 4\right) + (3x+6) + 4 & \\ & = & -x^2-4x-4+3x+6+4 & \\ & = & -x^2-x+6 & \end{array}\)

      To find \(f(x)+2\), we add \(2\) to the expression for \(f(x)\)

      \(\begin{array}{rclr} f(x) + 2 & = & \left(-x^2 + 3x + 4\right) + 2 & \\ & = & -x^2 + 3x + 6 \\ \end{array}\)

      From our work above, we see \(f(2) = 6\) so that

      \(\begin{array}{rclr} f(x) + f(2) & = & \left(-x^2 + 3x + 4\right) + 6 & \\ & = & -x^2 + 3x + 10 \\ \end{array}\)

2. Since \(f(x) = -x^2 + 3x + 4\), the equation \(f(x) = 4\) is equivalent to \(-x^2+3x+4 = 4\). Solving we get \(-x^2+3x = 0\), or \(x(-x+3) = 0\). We get \(x=0\) or \(x=3\), and we can verify these answers by checking that \(f(0) = 4\) and \(f(3) = 4\).

A few notes about Example 1.4.2 are in order. First note the difference between the answers for \(f(2x)\) and \(2f(x)\). For \(f(2x)\), we are multiplying the input by \(2\); for \(2 f(x)\), we are multiplying the output by \(2\). As we see, we get entirely different results. Along these lines, note that \(f(x+2)\), \(f(x) + 2\) and \(f(x) + f(2)\) are three different expressions as well. Even though function notation uses parentheses, as does multiplication, there is no general ‘distributive property’ of function notation. Finally, note the practice of using parentheses when substituting one algebraic expression into another; we highly recommend this practice as it will reduce careless errors.

Suppose now we wish to find \(r(3)\) for \(r(x) = \frac{2x}{x^2 - 9}\). Substitution gives

\[r(3) = \dfrac{2(3)}{(3)^2-9} = \dfrac{6}{0},\]

which is undefined. (Why is this, again?) The number \(3\) is not an allowable input to the function \(r\); in other words, \(3\) is not in the domain of \(r\). Which other real numbers are forbidden in this formula? We think back to arithmetic. The reason \(r(3)\) is undefined is because substitution results in a division by \(0\). To determine which other numbers result in such a transgression, we set the denominator equal to \(0\) and solve

\[\begin{array}{rclr} x^2 - 9 & = & 0 & \\ x^2 & = & 9 & \\ \sqrt{x^2} & = & \sqrt{9} & \mbox{extract square roots} \\ x & = & \pm 3 & \\ \end{array}\]

As long as we substitute numbers other than \(3\) and \(-3\), the expression \(r(x)\) is a real number. Hence, we write our domain in interval notation¹ as \((-\infty, -3) \cup (-3,3) \cup (3, \infty)\). When a formula for a function is given, we assume that the function is valid for all real numbers which make arithmetic sense when substituted into the formula. This set of numbers is often called the implied domain² of the function. At this stage, there are only two mathematical sins we need to avoid: division by \(0\) and extracting even roots of negative numbers. The following example illustrates these concepts.

Example 1.4.3

Find the domain³ of the following functions.

1. \(g(x) = \sqrt{4 - 3x}\)
2. \(h(x) = \sqrt[5]{4 - 3x}\)
3. \(f(x) = \dfrac{2}{1 - \dfrac{4x}{x-3}}\)
4. \(F(x) = \dfrac{\sqrt[4]{2x+1}}{x^2-1}\)
5. \(r(t) = \dfrac{4}{6 - \sqrt{t+3}}\)
6. \(I(x) = \dfrac{3x^2}{x}\)

Solution

1. The potential disaster for \(g\) is if the radicand⁴ is negative. To avoid this, we set \(4 - 3x \geq 0\). From this, we get \(3x \leq 4\) or \(x \leq \frac{4}{3}\). What this shows is that as long as \(x \leq \frac{4}{3}\), the expression \(4 - 3x \geq 0\), and the formula \(g(x)\) returns a real number. Our domain is \(\left(-\infty, \frac{4}{3}\right]\).
2. The formula for \(h(x)\) is hauntingly close to that of \(g(x)\) with one key difference \(-\) whereas the expression for \(g(x)\) includes an even indexed root (namely a square root), the formula for \(h(x)\) involves an odd indexed root (the fifth root). Since odd roots of real numbers (even negative real numbers) are real numbers, there is no restriction on the inputs to \(h\). Hence, the domain is \((-\infty, \infty)\).
3. In the expression for \(f\), there are two denominators. We need to make sure neither of them is \(0\). To that end, we set each denominator equal to \(0\) and solve. For the ‘small’ denominator, we get \(x - 3 = 0\) or \(x=3\). For the ‘large’ denominator

   \[\begin{array}{rclr} 1 - \dfrac{4x}{x-3} & = & 0 & \\ 1 & = & \dfrac{4x}{x-3} & \\ (1)(x-3) & = & \left(\dfrac{4x}{\cancel{x-3}}\right)\cancel{(x-3)} & \mbox{clear denominators} \\ x - 3 & = & 4x & \\ -3 & = & 3x \\ -1 & = & x \end{array}\]

   So we get two real numbers which make denominators \(0\), namely \(x = -1\) and \(x=3\). Our domain is all real numbers except \(-1\) and \(3\): \((-\infty, -1) \cup (-1,3) \cup (3, \infty)\).

4. In finding the domain of \(F\), we notice that we have two potentially hazardous issues: not only do we have a denominator, we have a fourth (even-indexed) root. Our strategy is to determine the restrictions imposed by each part and select the real numbers which satisfy both conditions. To satisfy the fourth root, we require \(2x+1 \geq 0\). From this we get \(2x \geq -1\) or \(x \geq -\frac{1}{2}\). Next, we round up the values of \(x\) which could cause trouble in the denominator by setting the denominator equal to \(0\). We get \(x^2 - 1=0\), or \(x = \pm 1\). Hence, in order for a real number \(x\) to be in the domain of \(F\), \(x \geq -\frac{1}{2}\) but \(x \neq \pm 1\). In interval notation, this set is \(\left[ -\frac{1}{2}, 1 \right) \cup (1, \infty)\).
5. Don’t be put off by the ‘\(t\)’ here. It is an independent variable representing a real number, just like \(x\) does, and is subject to the same restrictions. As in the previous problem, we have double danger here: we have a square root and a denominator. To satisfy the square root, we need a non-negative radicand so we set \(t + 3 \geq 0\) to get \(t \geq -3\). Setting the denominator equal to zero gives \(6 - \sqrt{t+3} =0\), or \(\sqrt{t+3} = 6\). Squaring both sides gives \(t+3 = 36\), or \(t = 33\). Since we squared both sides in the course of solving this equation, we need to check our answer.⁵ Sure enough, when \(t=33\), \(6 - \sqrt{t+3} = 6 - \sqrt{36} = 0\), so \(t=33\) will cause problems in the denominator. At last we can find the domain of \(r\): we need \(t \geq -3\), but \(t \neq 33\). Our final answer is \([-3, 33) \cup (33, \infty)\).
6. It’s tempting to simplify \(I(x) = \frac{3x^2}{x} = 3x\), and, since there are no longer any denominators, claim that there are no longer any restrictions. However, in simplifying \(I(x)\), we are assuming \(x \neq 0\), since \(\frac{0}{0}\) is undefined.⁶ Proceeding as before, we find the domain of \(I\) to be all real numbers except \(0\): \((-\infty, 0) \cup (0, \infty)\).

It is worth reiterating the importance of finding the domain of a function before simplifying, as evidenced by the function \(I\) in the previous example. Even though the formula \(I(x)\) simplifies to \(3x\), it would be inaccurate to write \(I(x) = 3x\) without adding the stipulation that \(x \neq 0\). It would be analogous to not reporting taxable income or some other sin of omission.

1.4.1 Modeling with Functions

The importance of Mathematics to our society lies in its value to approximate, or model real-world phenomenon. Whether it be used to predict the high temperature on a given day, determine the hours of daylight on a given day, or predict population trends of various and sundry real and mythical beasts,⁷ Mathematics is second only to literacy in the importance humanity’s development.⁸

It is important to keep in mind that anytime Mathematics is used to approximate reality, there are always limitations to the model. For example, suppose grapes are on sale at the local market for \(\$1.50\) per pound. Then one pound of grapes costs \(\$1.50\), two pounds of grapes cost \(\$3.00\), and so forth. Suppose we want to develop a formula which relates the cost of buying grapes to the amount of grapes being purchased. Since these two quantities vary from situation to situation, we assign them variables. Let \(c\) denote the cost of the grapes and let \(g\) denote the amount of grapes purchased. To find the cost \(c\) of the grapes, we multiply the amount of grapes \(g\) by the price \(\$1.50\) dollars per pound to get \[c = 1.5 g\] In order for the units to be correct in the formula, \(g\) must be measured in pounds of grapes in which case the computed value of \(c\) is measured in dollars. Since we’re interested in finding the cost \(c\) given an amount \(g\), we think of \(g\) as the independent variable and \(c\) as the dependent variable. Using the language of function notation, we write \[c(g) = 1.5 g\] where \(g\) is the amount of grapes purchased (in pounds) and \(c(g)\) is the cost (in dollars). For example, \(c(5)\) represents the cost, in dollars, to purchase \(5\) pounds of grapes. In this case, \(c(5) = 1.5(5) = 7.5\), so it would cost \(\$ 7.50\). If, on the other hand, we wanted to find the amount of grapes we can purchase for \(\$5\), we would need to set \(c(g) = 5\) and solve for \(g\). In this case, \(c(g)=1.5g\), so solving \(c(g) = 5\) is equivalent to solving \(1.5g = 5\) Doing so gives \(g = \frac{5}{1.5} = 3.\overline{3}\). This means we can purchase exactly \(3.\overline{3}\) pounds of grapes for \(\$5\). Of course, you would be hard-pressed to buy exactly \(3.\overline{3}\) pounds of grapes,⁹ and this leads us to our next topic of discussion, the applied domain¹⁰ of a function.

Even though, mathematically, \(c(g) = 1.5g\) has no domain restrictions (there are no denominators and no even-indexed radicals), there are certain values of \(g\) that don’t make any physical sense. For example, \(g = -1\) corresponds to ‘purchasing’ \(-1\) pounds of grapes.¹¹ Also, unless the ‘local market’ mentioned is the State of California (or some other exporter of grapes), it also doesn’t make much sense for \(g = 500,\!000,\!000\), either. So the reality of the situation limits what \(g\) can be, and these limits determine the applied domain of \(g\). Typically, an applied domain is stated explicitly. In this case, it would be common to see something like \(c(g) = 1.5g\), \(0 \leq g \leq 100\), meaning the number of pounds of grapes purchased is limited from \(0\) up to \(100\). The upper bound here, \(100\) may represent the inventory of the market, or some other limit as set by local policy or law. Even with this restriction, our model has its limitations. As we saw above, it is virtually impossible to buy exactly \(3.\overline{3}\) pounds of grapes so that our cost is exactly \(\$5\). In this case, being sensible shoppers, we would most likely ‘round down’ and purchase \(3\) pounds of grapes or however close the market scale can read to \(3.\overline{3}\) without being over. It is time for a more sophisticated example.

Example 1.4.4

The height \(h\) in feet of a model rocket above the ground \(t\) seconds after lift-off is given by \[h(t) = \left\{ \begin{array}{rcl} -5t^2 + 100t, & \mbox{if} & 0 \leq t \leq 20 \\ 0, & \mbox{if} & t > 20 \\ \end{array} \right.\]

1. Find and interpret \(h(10)\) and \(h(60)\).
2. Solve \(h(t) = 375\) and interpret your answers.

Solution.

1. We first note that the independent variable here is \(t\), chosen because it represents time. Secondly, the function is broken up into two rules: one formula for values of \(t\) between \(0\) and \(20\) inclusive, and another for values of \(t\) greater than 20. Since \(t=10\) satisfies the inequality \(0 \leq t \leq 20\), we use the first formula listed, \(h(t) = -5t^2 + 100t\), to find \(h(10)\). We get \(h(10) = -5(10)^2 + 100(10) = 500\). Since \(t\) represents the number of seconds since lift-off and \(h(t)\) is the height above the ground in feet, the equation \(h(10) = 500\) means that \(10\) seconds after lift-off, the model rocket is \(500\) feet above the ground. To find \(h(60)\), we note that \(t=60\) satisfies \(t > 20\), so we use the rule \(h(t) = 0\). This function returns a value of \(0\) regardless of what value is substituted in for \(t\), so \(h(60) = 0\). This means that \(60\) seconds after lift-off, the rocket is \(0\) feet above the ground; in other words, a minute after lift-off, the rocket has already returned to Earth.
2. Since the function \(h\) is defined in pieces, we need to solve \(h(t) = 375\) in pieces. For \(0 \leq t \leq 20\), \(h(t) = -5t^2 + 100t\), so for these values of \(t\), we solve \(-5t^2 + 100t = 375\). Rearranging terms, we get \(5t^2 - 100t + 375 = 0\), and factoring gives \(5(t-5)(t-15) = 0\). Our answers are \(t=5\) and \(t=15\), and since both of these values of \(t\) lie between \(0\) and \(20\), we keep both solutions. For \(t>20\), \(h(t) = 0\), and in this case, there are no solutions to \(0=375\). In terms of the model rocket, solving \(h(t) = 375\) corresponds to finding when, if ever, the rocket reaches \(375\) feet above the ground. Our two answers, \(t=5\) and \(t=15\) correspond to the rocket reaching this altitude twice – once \(5\) seconds after launch, and again \(15\) seconds after launch.¹²

The type of function in the previous example is called a piecewise-defined function, or ‘piecewise’ function for short. Many real-world phenomena, income tax formulas¹³ for example, are modeled by such functions.

By the way, if we wanted to avoid using a piecewise function in Example 1.4.4, we could have used \(h(t) = -5t^2 + 100t\) on the explicit domain \(0 \leq t \leq 20\) because after 20 seconds, the rocket is on the ground and stops moving. In many cases, though, piecewise functions are your only choice, so it’s best to understand them well.

Mathematical modeling is not a one-section topic. It’s not even a one-course topic as is evidenced by undergraduate and graduate courses in mathematical modeling being offered at many universities. Thus our goal in this section cannot possibly be to tell you the whole story. What we can do is get you started. As we study new classes of functions, we will see what phenomena they can be used to model. In that respect, mathematical modeling cannot be a topic in a book, but rather, must be a theme of the book. For now, we have you explore some very basic models in the Exercises because you need to crawl to walk to run. As we learn more about functions, we’ll help you build your own models and get you on your way to applying Mathematics to your world.

1.4.2 Exercises

In Exercises 1-10, find an expression for \(f(x)\) and state its domain.

1. \(f\) is a function that takes a real number \(x\) and performs the following three steps in the order given: (1) multiply by 2; (2) add 3; (3) divide by 4.
2. \(f\) is a function that takes a real number \(x\) and performs the following three steps in the order given: (1) add 3; (2) multiply by 2; (3) divide by 4.
3. \(f\) is a function that takes a real number \(x\) and performs the following three steps in the order given: (1) divide by 4; (2) add 3; (3) multiply by 2.
4. \(f\) is a function that takes a real number \(x\) and performs the following three steps in the order given: (1) multiply by 2; (2) add 3; (3) take the square root.
5. \(f\) is a function that takes a real number \(x\) and performs the following three steps in the order given: (1) add 3; (2) multiply by 2; (3) take the square root.
6. \(f\) is a function that takes a real number \(x\) and performs the following three steps in the order given: (1) add 3; (2) take the square root; (3) multiply by 2.
7. \(f\) is a function that takes a real number \(x\) and performs the following three steps in the order given: (1) take the square root; (2) subtract 13; (3) make the quantity the denominator of a fraction with numerator 4.
8. \(f\) is a function that takes a real number \(x\) and performs the following three steps in the order given: (1) subtract 13; (2) take the square root; (3) make the quantity the denominator of a fraction with numerator 4.
9. \(f\) is a function that takes a real number \(x\) and performs the following three steps in the order given: (1) take the square root; (2) make the quantity the denominator of a fraction with numerator 4; (3) subtract 13.
10. \(f\) is a function that takes a real number \(x\) and performs the following three steps in the order given: (1) make the quantity the denominator of a fraction with numerator 4; (2) take the square root; (3) subtract 13.

In Exercises 11-18, use the given function \(f\) to find and simplify the following:

• \(f(3)\)
• \(f(-1)\)
• \(f\left(\frac{3}{2} \right)\)
• \(f(4x)\)
• \(4f(x)\)
• \(f(-x)\)
• \(f(x-4)\)
• \(f(x) - 4\)
• \(f\left(x^2\right)\)

11. \(f(x) = 2x+1\)
12. \(f(x) = 3 - 4x\)
13. \(f(x) = 2 - x^2\)
14. \(f(x) = x^2 - 3x + 2\)
15. \(f(x) = \dfrac{x}{x-1}\)
16. \(f(x) = \dfrac{2}{x^{3}}\)
17. \(f(x) = 6\)
18. \(f(x) = 0\)

In Exercises 19-26, use the given function \(f\) to find and simplify the following:

• \(f(2)\)
• \(f(-2)\)
• \(f(2a)\)
• \(2 f(a)\)
• \(f(a+2)\)
• \(f(a) + f(2)\)
• \(f \left( \frac{2}{a} \right)\)
• \(\frac{f(a)}{2}\)
• \(f(a + h)\)

19. \(f(x) = 2x-5\)
20. \(f(x) = 5-2x\)
21. \(f(x) = 2x^2 - 1\)
22. \(f(x) = 3x^2+3x-2\)
23. \(f(x) = \sqrt{2x+1}\)
24. \(f(x) = 117\)
25. \(f(x) = \dfrac{x}{2}\)
26. \(f(x) = \dfrac{2}{x}\)

In Exercises 27-34, use the given function \(f\) to find \(f(0)\) and solve \(f(x) = 0\)

27. \(f(x) = 2x - 1\)
28. \(f(x) = 3 - \frac{2}{5} x\)
29. \(f(x) = 2x^2 - 6\)
30. \(f(x) = x^2 - x - 12\)
31. \(f(x) = \sqrt{x+4}\)
32. \(f(x) = \sqrt{1-2x}\)
33. \(f(x) = \dfrac{3}{4-x}\)
34. \(f(x) = \dfrac{3x^2-12x}{4-x^2}\)
35. Let \(f(x) = \left\{ \begin{array}{rcr} x + 5 & \mbox{ if } & x \leq -3 \\ \sqrt{9-x^2} & \mbox{ if } & -3 < x \leq 3 \\ -x+5 & \mbox{ if } & x > 3 \\ \end{array} \right.\) Compute the following function values.
    1. \(f(-4)\)
    2. \(f(-3)\)
    3. \(f(3)\)
    4. \(f(3.001)\)
    5. \(f(-3.001)\)
    6. \(f(2)\)
36. Let \({\displaystyle f(x) = \left\{ \begin{array}{rcr} x^{2} & \mbox{ if } & x \leq -1\\ \sqrt{1 - x^{2}} & \mbox{ if } & -1 < x \leq 1\\ x & \mbox{ if } & x > 1 \end{array} \right. }\) Compute the following function values.
    1. \(f(4)\)
    2. \(f(-3)\)
    3. \(f(1)\)
    4. \(f(0)\)
    5. \(f(-1)\)
    6. \(f(-0.999)\)

In Exercises 37-62, find the (implied) domain of the function.

37. \(f(x) = x^{4} - 13x^{3} + 56x^{2} - 19\)
38. \(f(x) = x^2 + 4\)
39. \(f(x) = \dfrac{x-2}{x+1}\)
40. \(f(x) = \dfrac{3x}{x^2+x-2}\)
41. \(f(x) = \dfrac{2x}{x^2+3}\)
42. \(f(x) = \dfrac{2x}{x^2-3}\)
43. \(f(x) = \dfrac{x+4}{x^2 - 36}\)
44. \(f(x) = \dfrac{x-2}{x-2}\)
45. \(f(x) = \sqrt{3-x}\)
46. \(f(x) = \sqrt{2x+5}\)
47. \(f(x) = 9x\sqrt{x+3}\)
48. \(f(x) = \dfrac{\sqrt{7-x}}{x^2+1}\)
49. \(f(x) = \sqrt{6x-2}\)
50. \(f(x) = \dfrac{6}{\sqrt{6x-2}}\)
51. \(f(x) = \sqrt[3]{6x-2}\)
52. \(f(x) = \dfrac{6}{4 - \sqrt{6x-2}}\)
53. \(f(x) = \dfrac{\sqrt{6x-2}}{x^2-36}\)
54. \(f(x) = \dfrac{\sqrt[3]{6x-2}}{x^2+36}\)
55. \(s(t) = \dfrac{t}{t - 8}\)
56. \(Q(r) = \dfrac{\sqrt{r}}{r - 8}\)
57. \(b(\theta) = \dfrac{\theta}{\sqrt{\theta - 8}}\)
58. \(A(x) = \sqrt{x - 7} + \sqrt{9 - x}\)
59. \(\alpha(y) = \sqrt[3]{\dfrac{y}{y - 8}}\)
60. \(g(v) = \dfrac{1}{4 - \dfrac{1}{v^{2}}}\)
61. \(T(t) = \dfrac{\sqrt{t} - 8}{5-t}\)
62. \(u(w) = \dfrac{w - 8}{5 - \sqrt{w}}\)
63. The area \(A\) enclosed by a square, in square inches, is a function of the length of one of its sides \(x\), when measured in inches. This relation is expressed by the formula \(A(x) = x^2\) for \(x > 0\). Find \(A(3)\) and solve \(A(x) = 36\). Interpret your answers to each. Why is \(x\) restricted to \(x > 0\)?
64. The area \(A\) enclosed by a circle, in square meters, is a function of its radius \(r\), when measured in meters. This relation is expressed by the formula \(A(r) = \pi r^2\) for \(r > 0\). Find \(A(2)\) and solve \(A(r) = 16\pi\). Interpret your answers to each. Why is \(r\) restricted to \(r > 0\)?
65. The volume \(V\) enclosed by a cube, in cubic centimeters, is a function of the length of one of its sides \(x\), when measured in centimeters. This relation is expressed by the formula \(V(x) = x^3\) for \(x > 0\). Find \(V(5)\) and solve \(V(x) = 27\). Interpret your answers to each. Why is \(x\) restricted to \(x > 0\)?
66. The volume \(V\) enclosed by a sphere, in cubic feet, is a function of the radius of the sphere \(r\), when measured in feet. This relation is expressed by the formula \(V(r) =\frac{4\pi}{3} r^{3}\) for \(r > 0\). Find \(V(3)\) and solve \(V(r) = \frac{32\pi}{3}\). Interpret your answers to each. Why is \(r\) restricted to \(r > 0\)?
67. The height of an object dropped from the roof of an eight story building is modeled by: \(h(t) = -16t^2 + 64\), \(0 \leq t \leq 2\). Here, \(h\) is the height of the object off the ground, in feet, \(t\) seconds after the object is dropped. Find \(h(0)\) and solve \(h(t) = 0\). Interpret your answers to each. Why is \(t\) restricted to \(0 \leq t \leq 2\)?
68. The temperature \(T\) in degrees Fahrenheit \(t\) hours after 6 AM is given by \(T(t) = -\frac{1}{2} t^2 + 8t+3\) for \(0 \leq t \leq 12\). Find and interpret \(T(0)\), \(T(6)\) and \(T(12)\).
69. The function \(C(x) = x^2-10x+27\) models the cost, in hundreds of dollars, to produce \(x\) thousand pens. Find and interpret \(C(0)\), \(C(2)\) and \(C(5)\).
70. Using data from the Bureau of Transportation Statistics, , the average fuel economy \(F\) in miles per gallon for passenger cars in the US can be modeled by \(F(t) = -0.0076t^2+0.45t + 16\), \(0 \leq t \leq 28\), where \(t\) is the number of years since \(1980\). Use your calculator to find \(F(0)\), \(F(14)\) and \(F(28)\). Round your answers to two decimal places and interpret your answers to each.
71. The population of Sasquatch in Portage County can be modeled by the function \(P(t) = \frac{150t}{t + 15}\), where \(t\) represents the number of years since 1803. Find and interpret \(P(0)\) and \(P(205)\). Discuss with your classmates what the applied domain and range of \(P\) should be.
72. For \(n\) copies of the book Me and my Sasquatch, a print on-demand company charges \(C(n)\) dollars, where \(C(n)\) is determined by the formula \[{\displaystyle C(n) = \left\{ \begin{array}{rcl} 15n & \mbox{ if } & 1 \leq n \leq 25 \\ 13.50n & \mbox{ if } & 25 < n \leq 50 \\ 12n & \mbox{ if } & n > 50 \\ \end{array} \right. }\]
    1. Find and interpret \(C(20)\).
    2. [50vs51] How much does it cost to order 50 copies of the book? What about 51 copies?
    3. Your answer to 72b should get you thinking. Suppose a bookstore estimates it will sell 50 copies of the book. How many books can, in fact, be ordered for the same price as those 50 copies? (Round your answer to a whole number of books.)
73. An on-line comic book retailer charges shipping costs according to the following formula \[{\displaystyle S(n) = \left\{ \begin{array}{rcl} 1.5 n + 2.5 & \mbox{ if } & 1 \leq n \leq 14 \\ 0 & \mbox{ if } & n \geq 15 \end{array} \right. }\]
    1. What is the cost to ship 10 comic books?
    2. What is the significance of the formula \(S(n) = 0\) for \(n \geq 15\)?
74. [piecewisemobile] The cost \(C\) (in dollars) to talk \(m\) minutes a month on a mobile phone plan is modeled by \[{\displaystyle C(m) = \left\{ \begin{array}{rcl} 25 & \mbox{ if } & 0 \leq m \leq 1000 \\ 25+0.1(m-1000) & \mbox{ if } & m > 1000 \end{array} \right. }\]
    1. How much does it cost to talk \(750\) minutes per month with this plan?
    2. How much does it cost to talk \(20\) hours a month with this plan?
    3. Explain the terms of the plan verbally.
75. In Section 1.1.1 we defined the set of integers as \(\mathbb{Z} = \{ \ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\}\).¹⁴ The greatest integer of , denoted by \(\lfloor x \rfloor\), is defined to be the largest integer \(k\) with \(k \leq x\).
    1. Find \(\lfloor 0.785 \rfloor\), \(\lfloor 117 \rfloor\), \(\lfloor -2.001 \rfloor\), and \(\lfloor \pi + 6 \rfloor\)
    2. Discuss with your classmates how \(\lfloor x \rfloor\) may be described as a piecewise defined function.

       HINT: There are infinitely many pieces!

    3. Is \(\lfloor a + b \rfloor = \lfloor a \rfloor + \lfloor b \rfloor\) always true? What if \(a\) or \(b\) is an integer? Test some values, make a conjecture, and explain your result.
76. We have through our examples tried to convince you that, in general, \(f(a + b) \neq f(a) + f(b)\). It has been our experience that students refuse to believe us so we’ll try again with a different approach. With the help of your classmates, find a function \(f\) for which the following properties are always true.
    1. \(f(0) = f(-1 + 1) = f(-1) + f(1)\)
    2. \(f(5) = f(2 + 3) = f(2) + f(3)\)
    3. \(f(-6) = f(0 - 6) = f(0) - f(6)\)
    4. \(f(a + b) = f(a) + f(b)\;\) regardless of what two numbers we give you for \(a\) and \(b\).

    How many functions did you find that failed to satisfy the conditions above? Did \(f(x) = x^{2}\) work? What about \(f(x) = \sqrt{x}\) or \(f(x) = 3x + 7\) or \(f(x) = \dfrac{1}{x}\)? Did you find an attribute common to those functions that did succeed? You should have, because there is only one extremely special family of functions that actually works here. Thus we return to our previous statement, in general, \(f(a + b) \neq f(a) + f(b)\).

Answers

1. \(f(x) = \frac{2x+3}{4}\)
   Domain: \((-\infty, \infty)\)

2. \(f(x) = \frac{2(x+3)}{4} = \frac{x+3}{2}\)
   Domain: \((-\infty, \infty)\)

3. \(f(x) = 2\left(\frac{x}{4} + 3\right) = \frac{1}{2} x + 6\)
   Domain: \((-\infty, \infty)\)

4. \(f(x) = \sqrt{2x+3}\)
   Domain: \(\left[ -\frac{3}{2}, \infty \right)\)

5. \(f(x) = \sqrt{2(x+3)} = \sqrt{2x+6}\)
   Domain: \([-3, \infty)\)

6. \(f(x) = 2\sqrt{x+3}\)
   Domain: \([-3, \infty)\)

7. \(f(x) = \frac{4}{\sqrt{x} - 13}\)
   Domain: \([0, 169) \cup (169, \infty)\)

8. \(f(x) = \frac{4}{\sqrt{x - 13}}\)
   Domain: \((13, \infty)\)

9. \(f(x) = \frac{4}{\sqrt{x}} - 13\)
   Domain: \((0, \infty)\)

10. \(f(x) = \sqrt{\frac{4}{x}} - 13 = \frac{2}{\sqrt{x}} - 13\)
    Domain: \((0, \infty)\)

11. For \(f(x) = 2x+1\)
    • \(f(3) = 7\)
    • \(f(-1) = -1\)
    • \(f\left(\frac{3}{2} \right) = 4\)
    • \(f(x-4) = 2x-7\)
    • \(f(x) - 4 = 2x-3\)
    • \(f\left(x^2\right) = 2x^2+1\)
    • \(f(4x) = 8x+1\)
    • \(4f(x) = 8x+4\)
    • \(f(-x) = -2x+1\)
12. For \(f(x) = 3-4x\)
    • \(f(3) = -9\)
    • \(f(-1) = 7\)
    • \(f\left(\frac{3}{2} \right) = -3\)
    • \(f(x-4) = 19-4x\)
    • \(f(x) - 4 = -4x-1\)
    • \(f\left(x^2\right) = 3-4x^2\)
    • \(f(4x) = 3-16x\)
    • \(4f(x) = 12-16x\)
    • \(f(-x) = 4x+3\)
13. For \(f(x) = 2 - x^2\)
    • \(f(3) = -7\)
    • \(f(-1) = 1\)
    • \(f\left(\frac{3}{2} \right) = -\frac{1}{4}\)
    • \(f(x-4) = -x^2+8x-14\)
    • \(f(x) - 4 = -x^{2} - 2\)
    • \(f\left(x^2\right) = 2-x^4\)
    • \(f(4x) = 2-16x^2\)
    • \(4f(x) = 8-4x^2\)
    • \(f(-x) = 2-x^2\)
14. For \(f(x) = x^2 - 3x + 2\)
    • \(f(3) = 2\)
    • \(f(-1) = 6\)
    • \(f\left(\frac{3}{2} \right) = -\frac{1}{4}\)
    • \(f(x-4) = x^2-11x+30\)
    • \(f(x) - 4 = x^2-3x-2\)
    • \(f\left(x^2\right) = x^4-3x^2+2\)
    • \(f(4x) = 16x^2-12x+2\)
    • \(4f(x) = 4x^2-12x+8\)
    • \(f(-x) = x^2+3x+2\)
15. For \(f(x) = \frac{x}{x-1}\)
    • \(f(3) = \frac{3}{2}\)
    • \(f(-1) = \frac{1}{2}\)
    • \(f\left(\frac{3}{2} \right) = 3\)
    • \(f(x-4) = \frac{x-4}{x-5}\)
    • \(f(x) - 4 = \frac{x}{x-1} - 4\)
    • \(\hphantom{f(x) - 4} = \frac{4-3x}{x-1}\)
    • \(f\left(x^2\right) = \frac{x^2}{x^2-1}\)
    • \(f(4x) = \frac{4x}{4x-1}\)
    • \(4f(x) = \frac{4x}{x-1}\)
    • \(f(-x) = \frac{x}{x+1}\)
16. For \(f(x) = \frac{2}{x^3}\)
    • \(f(3) = \frac{2}{27}\)
    • \(f(-1) = -2\)
    • \(f\left(\frac{3}{2} \right) = \frac{16}{27}\)
    • \(f(x-4) = \frac{2}{(x-4)^3}\)
    • \(=\frac{2}{x^3-12x^2+48x-64}\)
    • \(f(x) - 4 = \frac{2}{x^3} - 4\)
    • \(\hphantom{f(x) - 4} = \frac{2-4x^3}{x^3}\)
    • \(f\left(x^2\right) = \frac{2}{x^6}\)
    • \(f(4x) = \frac{1}{32x^3}\)
    • \(4f(x) = \frac{8}{x^3}\)
    • \(f(-x) = -\frac{2}{x^3}\)
17. For \(f(x) = 6\)
    • \(f(3) = 6\)
    • \(f(-1) =6\)
    • \(f\left(\frac{3}{2} \right) = 6\)
    • \(f(x-4) = 6\)
    • \(f(x) - 4 = 2\)
    • \(f\left(x^2\right) = 6\)
    • \(f(4x) = 6\)
    • \(4f(x) = 24\)
    • \(f(-x) = 6\)
18. For \(f(x) = 0\)
    • \(f(3) = 0\)
    • \(f(-1) =0\)
    • \(f\left(\frac{3}{2} \right) = 0\)
    • \(f(x-4) = 0\)
    • \(f(x) - 4 = -4\)
    • \(f\left(x^2\right) = 0\)
    • \(f(4x) = 0\)
    • \(4f(x) = 0\)
    • \(f(-x) = 0\)
19. For \(f(x) = 2x-5\)
    • \(f(2) = -1\)
    • \(f(-2) = -9\)
    • \(f(2a) = 4a-5\)
    • \(f \left( \frac{2}{a} \right) = \frac{4}{a} - 5\)
    • \(\hphantom{f \left( \frac{2}{a} \right)} = \frac{4-5a}{a}\)
    • \(\frac{f(a)}{2} =\frac{2a-5}{2}\)
    • \(f(a + h) = 2a + 2h - 5\)
    • \(2 f(a) = 4a-10\)
    • \(f(a+2) = 2a-1\)
    • \(f(a) + f(2) = 2a-6\)
20. For \(f(x) = 5-2x\)
    • \(f(2) = 1\)
    • \(f(-2) = 9\)
    • \(f(2a) = 5-4a\)
    • \(f \left( \frac{2}{a} \right) = 5 - \frac{4}{a}\)
    • \(\hphantom{f \left( \frac{2}{a} \right)} = \frac{5a-4}{a}\)
    • \(\frac{f(a)}{2} = \frac{5-2a}{2}\)
    • \(f(a + h) = 5-2a-2h\)
    • \(2 f(a) = 10-4a\)
    • \(f(a+2) = 1-2a\)
    • \(f(a) + f(2) = 6-2a\)
21. For \(f(x) = 2x^2-1\)
    • \(f(2) = 7\)
    • \(f(-2) = 7\)
    • \(f(2a) = 8a^2-1\)
    • \(f \left( \frac{2}{a} \right) = \frac{8}{a^2} - 1\)
    • \(\hphantom{f \left( \frac{2}{a} \right)} = \frac{8-a^2}{a^2}\)
    • \(\frac{f(a)}{2} = \frac{2a^2-1}{2}\)
    • \(f(a + h) = 2a^2+4ah+2h^2-1\)
    • \(2 f(a) = 4a^2-2\)
    • \(f(a+2) = 2a^2+8a+7\)
    • \(f(a) + f(2) = 2a^2+6\)
22. For \(f(x) = 3x^2+3x-2\)
    • \(f(2) = 16\)
    • \(f(-2) = 4\)
    • \(f(2a) = 12a^2+6a-2\)
    • \(f \left( \frac{2}{a} \right) = \frac{12}{a^2} + \frac{6}{a} - 2\)
    • \(\hphantom{f \left( \frac{2}{a} \right)} = \frac{12+6a-2a^2}{a^2}\)
    • \(\frac{f(a)}{2} = \frac{3a^2+3a-2}{2}\)
    • \(f(a + h) = 3a^2 + 6ah + 3h^2+3a+3h-2\)
    • \(2 f(a) = 6a^2+6a-4\)
    • \(f(a+2) = 3a^2+15a+16\)
    • \(f(a) + f(2) = 3a^2+3a+14\)
23. For \(f(x) = \sqrt{2x+1}\)
    • \(f(2) = \sqrt{5}\)
    • \(f(-2)\) is not real
    • \(f(2a) = \sqrt{4a+1}\)
    • \(f \left( \frac{2}{a} \right) = \sqrt{\frac{4}{a} + 1}\)
    • \(\hphantom{f \left( \frac{2}{a} \right)} = \sqrt{\frac{a+4}{a}}\)
    • \(\frac{f(a)}{2} = \frac{\sqrt{2a+1}}{2}\)
    • \(f(a + h) = \sqrt{2a+2h+1}\)
    • \(2 f(a) = 2\sqrt{2a+1}\)
    • \(f(a+2) = \sqrt{2a+5}\)
    • \(f(a) + f(2) =\sqrt{2a+1} + \sqrt{5}\)
24. For \(f(x) = 117\)
    • \(f(2) = 117\)
    • \(f(-2) = 117\)
    • \(f(2a) = 117\)
    • \(f \left( \frac{2}{a} \right) = 117\)
    • \(\frac{f(a)}{2} = \frac{117}{2}\)
    • \(f(a + h) = 117\)
    • \(2 f(a) = 234\)
    • \(f(a+2) = 117\)
    • \(f(a) + f(2) = 234\)
25. For \(f(x) = \frac{x}{2}\)
    • \(f(2) = 1\)
    • \(f(-2) = -1\)
    • \(f(2a) = a\)
    • \(f \left( \frac{2}{a} \right) = \frac{1}{a}\)
    • \(\frac{f(a)}{2} = \frac{a}{4}\)
    • \(f(a + h) = \frac{a+h}{2}\)
    • \(2 f(a) = a\)
    • \(f(a+2) = \frac{a+2}{2}\)

    • \(f(a) + f(2) = \frac{a}{2}+ 1\)
      \(\hphantom{f(a) + f(2)} = \frac{a+2}{2}\)

26. For \(f(x) = \frac{2}{x}\)
    • \(f(2) = 1\)
    • \(f(-2) = -1\)
    • \(f(2a) = \frac{1}{a}\)
    • \(f \left( \frac{2}{a} \right) = a\)
    • \(\frac{f(a)}{2} = \frac{1}{a}\)
    • \(f(a + h) = \frac{2}{a+h}\)
    • \(2 f(a) = \frac{4}{a}\)
    • \(f(a+2) = \frac{2}{a+2}\)

    • \(f(a) + f(2) = \frac{2}{a}+1\)
      \(\hphantom{f(a)+f(2)}=\frac{a+2}{2}\)

27. For \(f(x) = 2x-1\), \(f(0) = -1\) and \(f(x) = 0\) when \(x = \frac{1}{2}\)
28. For \(f(x) = 3 - \frac{2}{5} x\), \(f(0) = 3\) and \(f(x) = 0\) when \(x = \frac{15}{2}\)
29. For \(f(x) = 2x^2-6\), \(f(0) = -6\) and \(f(x) = 0\) when \(x = \pm \sqrt{3}\)
30. For \(f(x) = x^2-x-12\), \(f(0) = -12\) and \(f(x) = 0\) when \(x = -3\) or \(x=4\)
31. For \(f(x) = \sqrt{x+4}\), \(f(0) = 2\) and \(f(x) = 0\) when \(x =-4\)
32. For \(f(x) = \sqrt{1-2x}\), \(f(0) = 1\) and \(f(x) = 0\) when \(x = \frac{1}{2}\)
33. For \(\ f(x)=\frac{3}{4-x}, f(0)=\frac{3}{4}\) an \(\ f(x)\) ) is never equal to 0
34. For \(\ f(x)=\frac{3 x^{2}-12 x}{4-x^{2}}, f(0)=0\) an \(\ f(x)=0\) when \(\ x = 0\) or \(\ x = 4\)
35. 1. \(\ f(-4)=1\)
    2. \(\ f(-3)=2\)
    3. \(\ f(3)=0\)
    4. \(\ f(3.001)=1.999\)
    5. \(\ f(-3.001)=1.999\)
    6. \(\ f(2)=\sqrt{5}\)
36. 1. \(\ f(4)=4\)
    2. \(\ f(-3)=9\)
    3. \(\ f(1)=0\)
    4. \(\ f(0)=1\)
    5. \(\ f(-1)=1\)
    6. \(\ f(-0.999) \approx 0.0447\)
37. \(\ (-\infty, \infty)\)
38. \(\ (-\infty, \infty)\)
39. \(\ (-\infty,-1) \cup(-1, \infty)\)
40. \(\ (-\infty,-2) \cup(-2,1) \cup(1, \infty)\)
41. \(\ (-\infty, \infty)\)
42. \(\ (-\infty,-\sqrt{3}) \cup(-\sqrt{3}, \sqrt{3}) \cup(\sqrt{3}, \infty)\)
43. \(\ (-\infty,-6) \cup(-6,6) \cup(6, \infty)\)
44. \(\ (-\infty, 2) \cup(2, \infty)\)
45. \(\ (-\infty, 3]\)
46. \(\ \left[-\frac{5}{2}, \infty\right)\)
47. \(\ [-3, \infty)\)
48. \(\ (-\infty, 7]\)
49. \(\ \left[\frac{1}{3}, \infty\right)\)
50. \(\ \left(\frac{1}{3}, \infty\right)\)
51. \(\ (-\infty, \infty)\)
52. \(\ \left[\frac{1}{3}, 3\right) \cup(3, \infty)\)
53. \(\ \left[\frac{1}{3}, 6\right) \cup(6, \infty)\)
54. \(\ (-\infty, \infty)\)
55. \(\ (-\infty, 8) \cup(8, \infty)\)
56. \(\ [0,8) \cup(8, \infty)\)
57. \(\ (8, \infty)\)
58. \(\ [7,9]\)
59. \(\ (-\infty, 8) \cup(8, \infty)\)
60. \(\ \left(-\infty,-\frac{1}{2}\right) \cup\left(-\frac{1}{2}, 0\right) \cup\left(0, \frac{1}{2}\right) \cup\left(\frac{1}{2}, \infty\right)\)
61. \(\ [0,5) \cup(5, \infty)\)
62. \(\ [0,25) \cup(25, \infty)\)
63. \(\ A(3)=9\), so the area enclosed by a square with a side of length 3 inches is 9 square inches. The solutions to \(\ A(x) = 36\) are \(\ x=\pm 6\). Since \(\ x\) is restricted to \(\ x > 0\), we only keep \(\ x = 6\). This means for the area enclosed by the square to be 36 square inches, the length of the side needs to be 6 inches. Since \(\ x\) represents a length, \(\ x > 0\).
64. \(\ A(2)=4 \pi\), so the area enclosed by a circle with radius 2 is \(\ 4 \pi\) square meters. The solution to \(\ A(r)=16 \pi\) are \(\ r=\pm 4\). Since \(\ r\) is restricted to \(\ r > 0\), we only keep \(\ r = 4\). This means for the area enclosed by the circle to be \(\ 16 \pi\) square meters, the radius needs to be 4 meters. Since \(\ r\) represents a radius (length), \(\ r>0\).
65. \(\ V(5)=125\), so the volume enclosed by a cube with a side of length 5 centimeters is 125 cubic centimeters. The solutio to \(\ V(x)=27\) is \(\ x = 3\). This means for the volume enclosed by the cube to be 27 cubic centimeters, the length of the side needs to 3 centimeters. Since \(\ x\) represents a length, \(\ x>0\).
66. \(\ V(3)=36 \pi\), so the volume enclosed by a sphere with radius 3 is \(\ 36 \pi\) cubic feet. The solution to \(\ V(r)=\frac{32 \pi}{3}\) is \(\ r=2\). This means for the volume enclosed by the sphere \(\ \frac{32 \pi}{3}\) cubic feet, the radius needs to 2 feet. Since \(\ r\) represents a radius (length), \(\ r>0\).
67. \(\ h(0)=64\), so at the moment the object is dropped off the building, the object is 64 feet off of the ground. The solutio to \(\ h(t)=0\) are \(\ t=\pm 2\). Since we restrict \(\ 0 \leq t \leq 2\), we only keep \(\ t = 2\). This means 2 seconds after the object is dropped off the building, it is 0 feet off the ground. Said differently, the object hits the ground after 2 seconds. The restriction \(\ 0 \leq t \leq 2\) restricts the time to be between the moment the object is released and the moment it hits the ground.
68. \(\ T(0)=3\), so at 6 AM (0 hours after 6 AM), it is \(\ 3^{\circ}\) Fahrenheit. \(\ T(6)=33\), so at noon (6 hours after 6 AM), the temperature is \(\ 33^{\circ}\) Fahrenheit. \(\ T(12)=27\), so at 6 PM (12 hours after 6 AM), it is \(\ 27^{\circ}\) Fahrenheit.
69. \(\ C(0)=27\), so to make 0 pens, it costs¹⁵ $2700. \(\ C(2)=11\), so to make 2000 pens, it costs $1100. \(\ C(5)=2\), so to make 5000 pens, it costs $2000.
70. \(\ F(0)=16.00\), so in 1980 (0 years after 1980), the average fuel economy of passenger cars in the US was 16.00 miles per gallon. \(\ F(14)=20.81\), so in 1994 (14 years after 1980), the average fuel economy of passenger cars in the US was 20.81 miles per gallon. \(\ F(28)=22.64\), so in 2008 (28 years after 1980), the average fuel economy of passenger cars in the US was 22.64 miles per gallon.
71. \(\ P(0)=0\) which means in 1803 (0 years after 1803), there are no Sasquatch in Portage County. \(\ P(205)=\frac{3075}{22} \approx 139.77\), so in 2008 (205 years after 1803), there were between 139 and 140 Sasquatch in Portage County.
72. 1. \(\ C(20)=300\). It costs $300 for 20 copies of the book.
    2. \(\ C(50)=675\), so it costs $675 for 50 copies of the book. \(\ C(51)=612\), so it costs $612 for 51 copies of the book.
    3. 56 books.
73. 1. \(\ S(10)=17.5\), so it costs $17.50 to ship 10 comic books.
    2. There is free shipping on orders of 15 or more comic books.
74. 1. \(\ C(750) = 25\), so it costs $25 to talk 750 minutes per month with this plan.
    2. Since 20 hours = 1200 minutes, we substitute \(\ m\) = 1200 and get \(\ C(1200) = 45\). It costs $45 to talk 20 hours per month with this plan.
    3. It costs $25 for up to 1000 minutes and 10 cents per minute for each minute over 1000 minutes.
75. 1. \(\ \lfloor 0.785\rfloor=0,\lfloor 117\rfloor=117,\lfloor-2.001\rfloor=-3, \text { and }\lfloor\pi+6\rfloor=9\)

---

Reference

¹ See the Exercises for Section 1.1.

² or, ‘implicit domain’

³ The word ‘implied’ is, well, implied.

⁴ The ‘radicand’ is the expression ‘inside’ the radical.

⁵ Do you remember why? Consider squaring both sides to ‘solve’ \(\ \sqrt{t+1}=-2\).

⁶ More precisely, the fraction \(\ \frac{0}{0}\) is an ‘indeterminant form’. Calculus is required tame such beasts.

⁷ See Sections 2.5, 11.1, and 6.5, respectively.

⁸ In Carl’s humble opinion, of course . . .

⁹ You could get close... within a certain specified margin of error, perhaps.

¹⁰ or, ‘explicit domain’

¹¹ Maybe this means returning a pound of grapes?

¹² What goes up . . .

¹³ See the Internal Revenue Service’s website

¹⁴ The use of the letter \(\ \mathbb{Z}\) for the integers is ostensibly because the German word zahlen means ‘to count.’

¹⁵ This is called the ‘fixed’ or ‘start-up’ cost. We’ll revisit this concept on page 82.