8.1: Long division

Last updated
Save as PDF

Page ID: 48996

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

We now show how to divide two polynomials. The method is similar to the long division of natural numbers. Our first example shows the procedure in full detail.

Example $\PageIndex{1}$

Divide the following fractions via long division:

$\dfrac{3571}{11}$
$\dfrac{x^3+5x^2+4x+2}{x+3}$

Solution

Recall the procedure for long division of natural numbers:

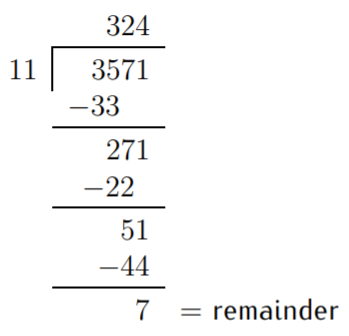
$clipboard_eeb7697e1afc4c40945de83b978221c5a.png$

The steps above are performed as follows. First, we find the largest multiple of $11$ less or equal to $35$. The answer $3$ is written as the first digit on the top line. Multiply $3$ times $11$, and subtract the answer $33$ from the first two digits $35$ of the dividend. The remaining digits $71$ are copied below to give $271$. Now we repeat the procedure, until we arrive at the remainder $7$. In short, what we have shown is that:

\[3571=324\cdot 11 +7\quad\text{ or alternatively, }\quad \dfrac{3571}{11}=324+\dfrac{7}{11} \nonumber \]

We repeat the steps from part (a) as follows. First, write the dividend and divisor in the above format:

Next, consider the highest term $x^3$ of the dividend and the highest term $x$ of the divisor. Since $\dfrac{x^3}{x}=x^2$, we start with the first term $x^2$ of the quotient:

Step 1:

\[\begin{array}{r}
x^2 \qquad \quad \phantom{)} \\
x+3{\overline{\smash{\big)}\,x ^ { 3 } + 5 x ^ { 2 } + 4 x + 2 \phantom{)}}}\\
\phantom{)}
\end{array} \nonumber \]

Multiply $x^2$ by the divisor $x+3$ and write it below the dividend:

Step 2:

\[\begin{array}{r}
x^2 \qquad \quad \phantom{)} \\
x+3{\overline{\smash{\big)}\,x ^ { 3 } + 5 x ^ { 2 } + 4 x + 2 \phantom{)}}}\\
{x^3+3x^2\qquad \qquad \;}\\
\phantom{)}
\end{array} \nonumber \]

Since we need to subtract $x^3+3x^2$, so we equivalently add its negative (don’t forget to distribute the negative):

Step 3:

\[\begin{array}{r}
x^2 \qquad \quad \phantom{)} \\
x+3{\overline{\smash{\big)}\,x^3+ 5x^2+4x+2 \phantom{)}}}\\
{\underline {-(x^3+3x^2)\qquad \qquad }\;}\\
2x^2\qquad \qquad \;\; \\
\phantom{)}
\end{array} \nonumber \]

Now, carry down the remaining terms of the dividend:

Step 4:

\[\begin{array}{r}
x^2 \qquad \quad \phantom{)} \\
x+3{\overline{\smash{\big)}\,x^3+ 5x^2+4x+2 \phantom{)}}}\\
{\underline {-(x^3+3x^2)\qquad \qquad }\;}\\
2x^2+4x+2 \;\; \\
\phantom{)}
\end{array} \nonumber \]

Now, repeat steps 1-4 for the remaining polynomial $2x^2+4x+2$. The outcome after going through steps 1-4 is the following:

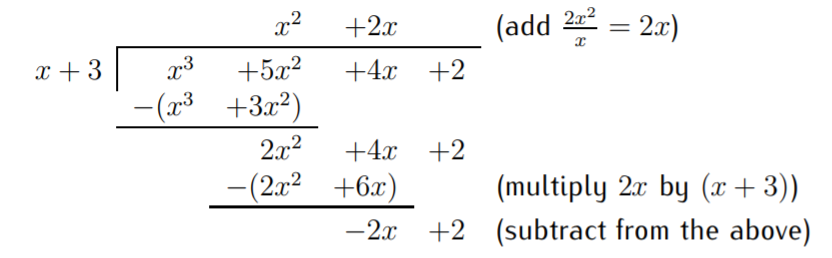
$clipboard_e0b594a879f1330ce8a859f577355b8f8.png$

Since $x$ can be divided into $-2x$, we can proceed with the above steps 1-4 one more time. The outcome is this:

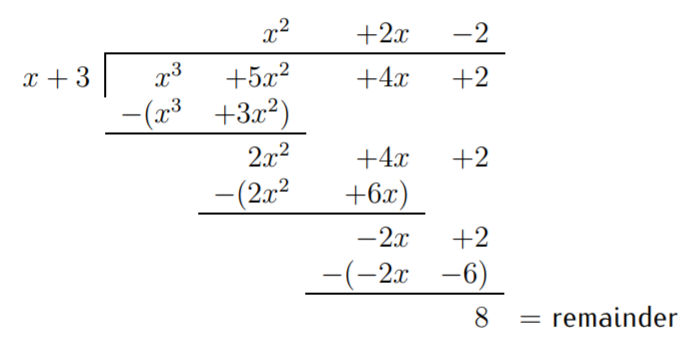
$clipboard_e8c07e409ef28fad6bd113a642c2b826b.png$

Note that now $x$ cannot be divided into $8$ so we stop here. The final term $8$ is called the remainder. The term $x^2+2x-2$ is called the quotient. In analogy with our result in part (a), we can write our conclusion as:

\[x^3+5x^2+4x+2=(x^2+2x-2)\cdot (x+3)+8 \nonumber \]

Alternatively, we could also divide this by $(x+3)$ and write it as:

\[\dfrac{x^3+5x^2+4x+2}{x+3}=x^2+2x-2+\dfrac{8}{x+3} \nonumber \]

Note

Just as with a division operation involving numbers, when dividing $\dfrac{f(x)}{g(x)}$, $f(x)$ is called the dividend and $g(x)$ is called the divisor. As a result of dividing $f(x)$ by $g(x)$ via long division with quotient $q(x)$ and remainder $r(x)$, we can write

\[\dfrac{f(x)}{g(x)} = q(x)+\dfrac{r(x)}{g(x)} \nonumber \]

If we multiply this equation by $g(x)$, we obtain the following alternative version:

\[f(x)=q(x)\cdot g(x)+r(x) \nonumber \]

Example $\PageIndex{2}$

Divide the following fractions via long division.

$\dfrac{x^2+4x+5}{x-4}$
$\dfrac{x^4+3x^3-5x+1}{x+1}$
$\dfrac{4x^3+2x^2+6x+18}{2x+3}$
$\dfrac{x^3+x^2+2x+1}{x^2+3x+1}$

Solution

For part (a), we calculate:

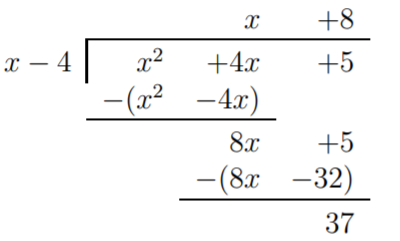
$clipboard_e7d78d13200bacd77e535af21baff3bde.png$

Therefore, $x^2+4x+5=(x+8)\cdot(x-4)+37$.

Now, for part (b), there is no $x^2$ term in the dividend. This can be resolved by adding $+0\, x^2$ to the dividend:

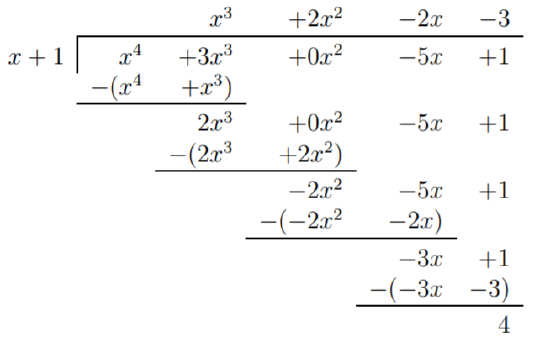
$clipboard_e9c652f243e301e871d6e01cf0626df24.png$

Therefore, we showed:

\[\dfrac{x^4+3x^3-5x+1}{x+1}=x^3+2x^2-2x-3+\dfrac{4}{x+1} \nonumber \]

For (c), calculate:

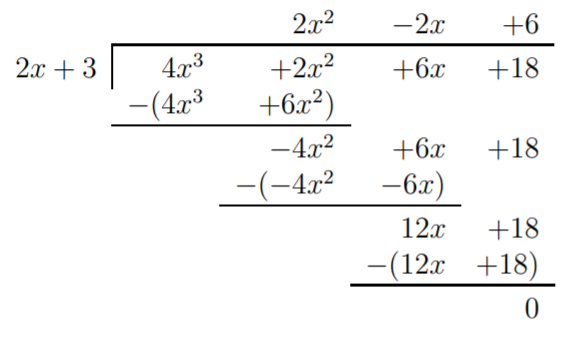
$clipboard_e91f3b39c060bd6e7b9d3490048dfd1d9.png$

Since the remainder is zero, we succeeded in factoring $4x^3+2x^2+6x+18$:

\[4x^3+2x^2+6x+18=(2x^2-2x+6)\cdot (2x+3) \nonumber \]

d) The last example has a divisor that is a polynomial of degree $2$. Therefore, the remainder is not a number, but a polynomial of degree $1$.

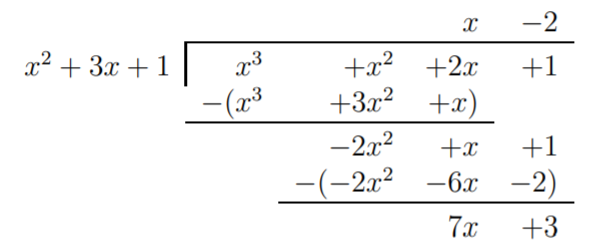
$clipboard_ed618933bb03f74546f3b31012d35898a.png$

Here, the remainder is $r(x)=7x+3$.

\[\dfrac{x^3+x^2+2x+1}{x^2+3x+1}= x-2+\dfrac{7x+3}{x^2+3x+1} \nonumber \]

Note

The divisor $g(x)$ is a factor of $f(x)$ exactly when the remainder $r(x)$ is zero, that is:

\[f(x)=q(x)\cdot g(x)\quad \iff\quad r(x)=0 \nonumber \]

For example, in the above Example $\PageIndex{3}$, only part (c) results in a factorization of the dividend, since this is the only part with remainder zero.

Search

Text Color

Text Size

Margin Size

Font Type

Example \(\PageIndex{1}\)

Note

Example \(\PageIndex{2}\)

Note