3.3: Power Functions and Polynomial Functions
- Page ID
- 1345
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Identify power functions.
- Identify end behavior of power functions.
- Identify polynomial functions.
- Identify the degree and leading coefficient of polynomial functions.
Suppose a certain species of bird thrives on a small island. Its population over the last few years is shown in Table \(\PageIndex{1}\).
| Year | 2009 | 2010 | 2011 | 2012 | 2013 |
|---|---|---|---|---|---|
| Bird Population | 800 | 897 | 992 | 1,083 | 1,169 |
The population can be estimated using the function \(P(t)=−0.3t^3+97t+800\), where \(P(t)\) represents the bird population on the island \(t\) years after 2009. We can use this model to estimate the maximum bird population and when it will occur. We can also use this model to predict when the bird population will disappear from the island. In this section, we will examine functions that we can use to estimate and predict these types of changes.

Identifying Power Functions
In order to better understand the bird problem, we need to understand a specific type of function. A power function is a function with a single term that is the product of a real number, a coefficient, and a variable raised to a fixed real number. (A number that multiplies a variable raised to an exponent is known as a coefficient.)
As an example, consider functions for area or volume. The function for the area of a circle with radius \(r\) is
\[A(r)={\pi}r^2 \nonumber\]
and the function for the volume of a sphere with radius \(r\) is
\[V(r)=\dfrac{4}{3}{\pi}r^3 \nonumber\]
Both of these are examples of power functions because they consist of a coefficient, \({\pi}\) or \(\dfrac{4}{3}{\pi}\), multiplied by a variable \(r\) raised to a power.
Definition: Power Function
A power function is a function that can be represented in the form
\[f(x)=kx^p \label{power}\]
where \(k\) and \(p\) are real numbers, and \(k\) is known as the coefficient.
Q&A: Is \(f(x)=2^x\) a power function?
No. A power function contains a variable base raised to a fixed power (Equation \ref{power}). This function has a constant base raised to a variable power. This is called an exponential function, not a power function. This function will be discussed later.
Example \(\PageIndex{1}\): Identifying Power Functions
Which of the following functions are power functions?
\[\begin{align*} f(x)&=1 &\text{Constant function} \\f(x)&=x &\text{Identify function} \\f(x)&=x^2 &\text{Quadratic function} \\ f(x)&=x^3 &\text{Cubic function} \\ f(x)&=\dfrac{1}{x} &\text{Reciprocal function} \\f(x)&=\dfrac{1}{x^2} &\text{Reciprocal squared function} \\ f(x)&=\sqrt{x} &\text{Square root function} \\ f(x)&=\sqrt[3]{x} &\text{Cube root function} \end{align*}\]
Solution
All of the listed functions are power functions.
The constant and identity functions are power functions because they can be written as \(f(x)=x^0\) and \(f(x)=x^1\) respectively.
The quadratic and cubic functions are power functions with whole number powers \(f(x)=x^2\) and \(f(x)=x^3\).
The reciprocal and reciprocal squared functions are power functions with negative whole number powers because they can be written as \(f(x)=x^{−1}\) and \(f(x)=x^{−2}\).
The square and cube root functions are power functions with fractional powers because they can be written as \(f(x)=x^{1/2}\) or \(f(x)=x^{1/3}\).
Exercise \(\PageIndex{1}\)
Which functions are power functions?
- \(f(x)=2x^2⋅4x^3\)
- \(g(x)=−x^5+5x^3−4x\)
- \(h(x)=\frac{2x^5−1}{3x^2+4}\)
- Answer
-
\(f(x)\) is a power function because it can be written as \(f(x)=8x^5\). The other functions are not power functions.
Identifying End Behavior of Power Functions
Figure \(\PageIndex{2}\) shows the graphs of \(f(x)=x^2\), \(g(x)=x^4\) and and \(h(x)=x^6\), which are all power functions with even, whole-number powers. Notice that these graphs have similar shapes, very much like that of the quadratic function in the toolkit. However, as the power increases, the graphs flatten somewhat near the origin and become steeper away from the origin.
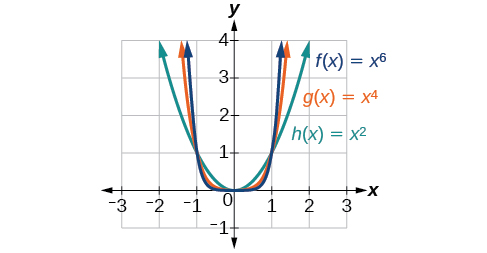
To describe the behavior as numbers become larger and larger, we use the idea of infinity. We use the symbol \(\infty\) for positive infinity and \(−\infty\) for negative infinity. When we say that “x approaches infinity,” which can be symbolically written as \(x{\rightarrow}\infty\), we are describing a behavior; we are saying that \(x\) is increasing without bound.
With the even-power function, as the input increases or decreases without bound, the output values become very large, positive numbers. Equivalently, we could describe this behavior by saying that as \(x\) approaches positive or negative infinity, the \(f(x)\) values increase without bound. In symbolic form, we could write
\[\text{as } x{\rightarrow}{\pm}{\infty}, \;f(x){\rightarrow}{\infty} \nonumber\]
Figure \(\PageIndex{3}\) shows the graphs of \(f(x)=x^3\), \(g(x)=x^5\), and \(h(x)=x^7\), which are all power functions with odd, whole-number powers. Notice that these graphs look similar to the cubic function in the toolkit. Again, as the power increases, the graphs flatten near the origin and become steeper away from the origin.
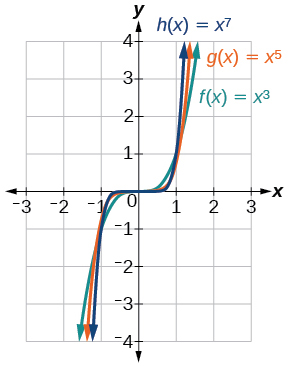
These examples illustrate that functions of the form \(f(x)=x^n\) reveal symmetry of one kind or another. First, in Figure \(\PageIndex{2}\) we see that even functions of the form \(f(x)=x^n\), \(n\) even, are symmetric about the \(y\)-axis. In Figure \(\PageIndex{3}\) we see that odd functions of the form \(f(x)=x^n\), \(n\) odd, are symmetric about the origin.
For these odd power functions, as \(x\) approaches negative infinity, \(f(x)\) decreases without bound. As \(x\) approaches positive infinity, \(f(x)\) increases without bound. In symbolic form we write
\[\begin{align*} &\text{as }x{\rightarrow}-{\infty},\;f(x){\rightarrow}-{\infty} \\ &\text{as }x{\rightarrow}{\infty},\;f(x){\rightarrow}{\infty} \end{align*}\]
The behavior of the graph of a function as the input values get very small \((x{\rightarrow}−{\infty})\) and get very large \(x{\rightarrow}{\infty}\) is referred to as the end behavior of the function. We can use words or symbols to describe end behavior.
Figure \(\PageIndex{4}\) shows the end behavior of power functions in the form \(f(x)=kx^n\) where \(n\) is a non-negative integer depending on the power and the constant.
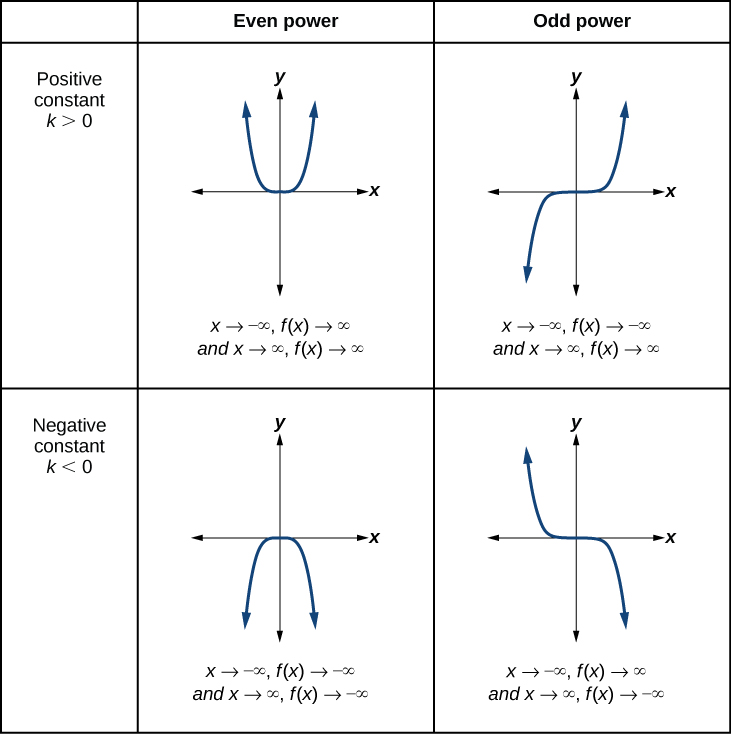
How To: Given a power function \(f(x)=kx^n\) where \(n\) is a non-negative integer, identify the end behavior.
- Determine whether the power is even or odd.
- Determine whether the constant is positive or negative.
- Use Figure \(\PageIndex{4}\) to identify the end behavior.
Example \(\PageIndex{2}\): Identifying the End Behavior of a Power Function
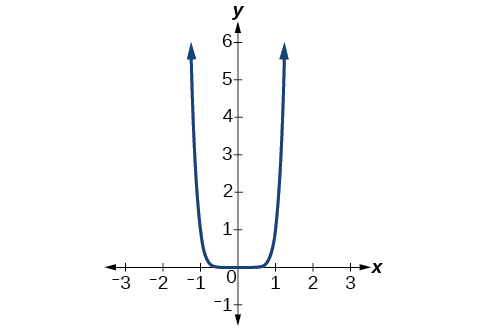
Describe the end behavior of the graph of \(f(x)=x^8\).
Solution
The coefficient is 1 (positive) and the exponent of the power function is 8 (an even number). As \(x\) approaches infinity, the output (value of \(f(x)\) ) increases without bound. We write as \(x→∞,\) \(f(x)→∞.\) As \(x\) approaches negative infinity, the output increases without bound. In symbolic form, as \(x→−∞,\) \(f(x)→∞.\) We can graphically represent the function as shown in Figure \(\PageIndex{5}\).
Example \(\PageIndex{3}\): Identifying the End Behavior of a Power Function.
Describe the end behavior of the graph of \(f(x)=−x^9\).
Solution
The exponent of the power function is 9 (an odd number). Because the coefficient is –1 (negative), the graph is the reflection about the \(x\)-axis of the graph of \(f(x)=x^9\). Figure \(\PageIndex{6}\) shows that as \(x\) approaches infinity, the output decreases without bound. As \(x\) approaches negative infinity, the output increases without bound. In symbolic form, we would write
\[\begin{align*} \text{as }x{\rightarrow}-{\infty},\;f(x){\rightarrow}{\infty} \\ \text{as }x{\rightarrow}{\infty},\;f(x){\rightarrow}-{\infty} \end{align*}\]
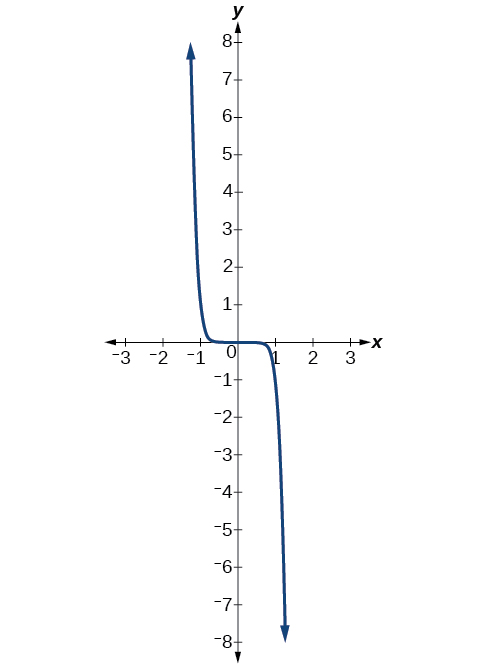
Analysis
We can check our work by using the table feature on a graphing utility.
| \(x\) | \(f(x)\) |
|---|---|
| -10 | 1,000,000,000 |
| -5 | 1,953,125 |
| 0 | 0 |
| 5 | -1,953,125 |
| 10 | -1,000,000,000 |
We can see from Table \(\PageIndex{2}\) that, when we substitute very small values for \(x\), the output is very large, and when we substitute very large values for \(x\), the output is very small (meaning that it is a very large negative value).
Exercise \(\PageIndex{2}\)
Describe in words and symbols the end behavior of \(f(x)=−5x^4\).
- Answer
-
As \(x\) approaches positive or negative infinity, \(f(x)\) decreases without bound: as \(x{\rightarrow}{\pm}{\infty}\), \(f(x){\rightarrow}−{\infty}\) because of the negative coefficient.
Identifying Polynomial Functions
An oil pipeline bursts in the Gulf of Mexico, causing an oil slick in a roughly circular shape. The slick is currently 24 miles in radius, but that radius is increasing by 8 miles each week. We want to write a formula for the area covered by the oil slick by combining two functions. The radius \(r\) of the spill depends on the number of weeks \(w\) that have passed. This relationship is linear.
\[r(w)=24+8w \nonumber\]
We can combine this with the formula for the area A of a circle.
\[A(r)={\pi}r^2 \nonumber\]
Composing these functions gives a formula for the area in terms of weeks.
\[ \begin{align*} A(w)&=A(r(w)) \\ &=A(24+8w) \\ & ={\pi}(24+8w)^2 \end{align*}\]
Multiplying gives the formula.
\[A(w)=576{\pi}+384{\pi}w+64{\pi}w^2 \nonumber\]
This formula is an example of a polynomial function. A polynomial function consists of either zero or the sum of a finite number of non-zero terms, each of which is a product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.
Definition: Polynomial Functions
Let \(n\) be a non-negative integer. A polynomial function is a function that can be written in the form
\[f(x)=a_nx^n+...+a_2x^2+a_1x+a_0 \label{poly}\]
This is called the general form of a polynomial function. Each \(a_i\) is a coefficient and can be any real number. Each product \(a_ix^i\) is a term of a polynomial function.
Example \(\PageIndex{4}\): Identifying Polynomial Functions
Which of the following are polynomial functions?
- \(f(x)=2x^3⋅3x+4\)
- \(g(x)=−x(x^2−4)\)
- \(h(x)=5\sqrt{x}+2\)
Solution
The first two functions are examples of polynomial functions because they can be written in the form of Equation \ref{poly}, where the powers are non-negative integers and the coefficients are real numbers.
- \(f(x)\) can be written as \(f(x)=6x^4+4\).
- \(g(x)\) can be written as \(g(x)=−x^3+4x\).
- \(h(x)\) cannot be written in this form and is therefore not a polynomial function.
Identifying the Degree and Leading Coefficient of a Polynomial Function
Because of the form of a polynomial function, we can see an infinite variety in the number of terms and the power of the variable. Although the order of the terms in the polynomial function is not important for performing operations, we typically arrange the terms in descending order of power, or in general form. The degree of the polynomial is the highest power of the variable that occurs in the polynomial; it is the power of the first variable if the function is in general form. The leading term is the term containing the highest power of the variable, or the term with the highest degree. The leading coefficient is the coefficient of the leading term.
Terminology of Polynomial Functions
We often rearrange polynomials so that the powers are descending.
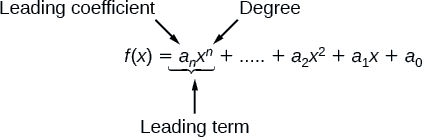
When a polynomial is written in this way, we say that it is in general form.
How To: Given a polynomial function, identify the degree and leading coefficient
- Find the highest power of \(x\) to determine the degree function.
- Identify the term containing the highest power of \(x\) to find the leading term.
- Identify the coefficient of the leading term.
Example \(\PageIndex{5}\): Identifying the Degree and Leading Coefficient of a Polynomial Function
Identify the degree, leading term, and leading coefficient of the following polynomial functions.
\(f(x)=3+2x^2−4x^3\)
\(g(t)=5t^5−2t^3+7t\)
\(h(p)=6p−p^3−2\)
Solution
For the function \(f(x)\), the highest power of \(x\) is 3, so the degree is 3. The leading term is the term containing that degree, \(−4x^3\). The leading coefficient is the coefficient of that term, −4.
For the function \(g(t)\), the highest power of \(t\) is 5, so the degree is 5. The leading term is the term containing that degree, \(5t^5\). The leading coefficient is the coefficient of that term, 5.
For the function \(h(p)\), the highest power of \(p\) is 3, so the degree is 3. The leading term is the term containing that degree, \(−p^3\); the leading coefficient is the coefficient of that term, −1.
Exercise \(\PageIndex{3}\)
Identify the degree, leading term, and leading coefficient of the polynomial \(f(x)=4x^2−x^6+2x−6\).
- Answer
-
The degree is \(6.\) The leading term is \(−x^6\). The leading coefficient is \(−1.\)
Identifying End Behavior of Polynomial Functions
Knowing the degree of a polynomial function is useful in helping us predict its end behavior. To determine its end behavior, look at the leading term of the polynomial function. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as \(x\) gets very large or very small, so its behavior will dominate the graph. For any polynomial, the end behavior of the polynomial will match the end behavior of the term of highest degree (Table \(\PageIndex{3}\)).
| Polynomial Function | Leading Term | Graph of Polynomial Function |
|---|---|---|
| \(f(x)=5x^4+2x^3−x−4\) | \(5x^4\) | 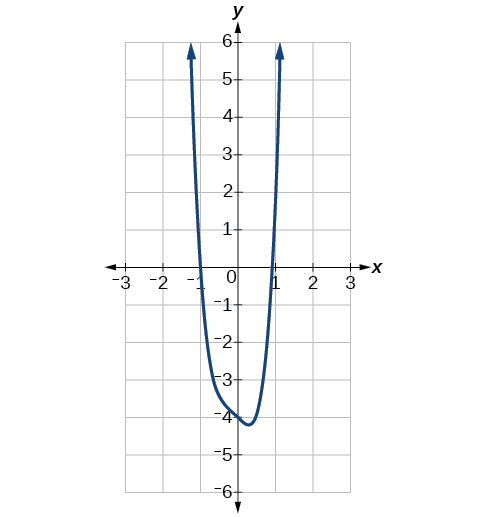 |
| \(f(x)=−2x^6−x^5+3x^4+x^3\) | \(−2x^6\) | 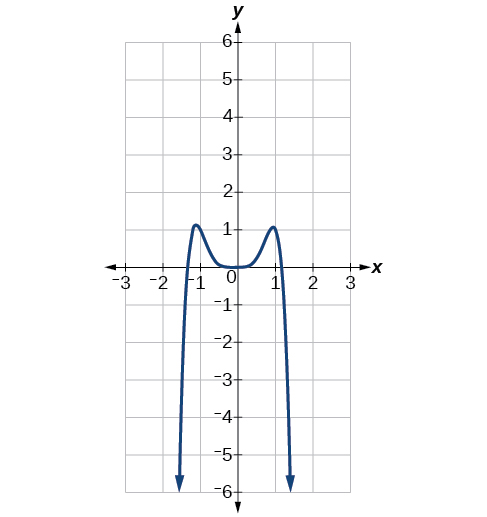 |
| \(f(x)=3x^5−4x^4+2x^2+1\) | \(3x^5\) | 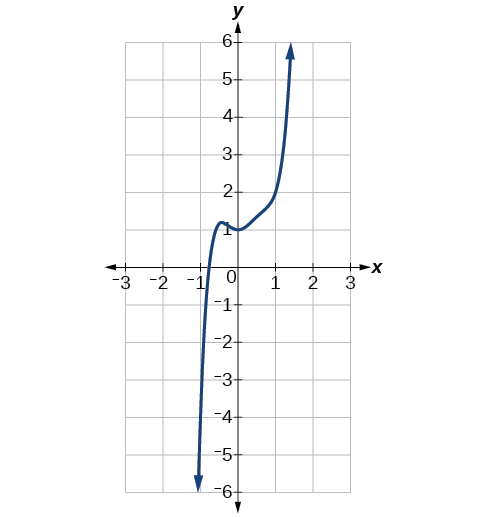 |
| \(f(x)=−6x^3+7x^2+3x+1\) | \(−6x^3\) | 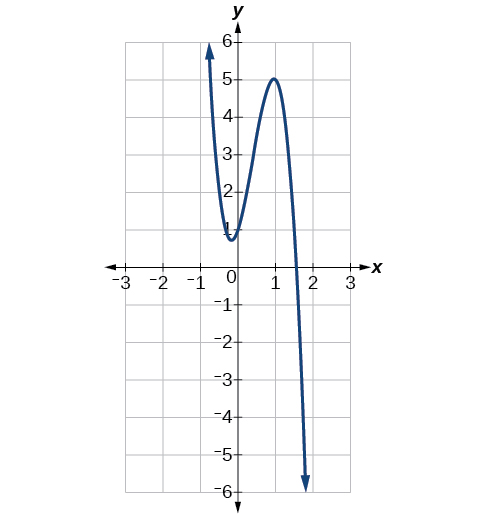 |
Example \(\PageIndex{6}\): Identifying End Behavior and Degree of a Polynomial Function
Describe the end behavior and determine a possible degree of the polynomial function in Figure \(\PageIndex{8}\).
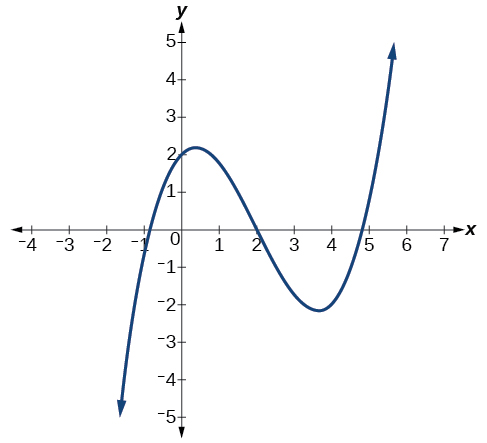
Solution
As the input values \(x\) get very large, the output values \(f(x)\) increase without bound. As the input values \(x\) get very small, the output values \(f(x)\) decrease without bound. We can describe the end behavior symbolically by writing
\[\text{as } x{\rightarrow}{\infty}, \; f(x){\rightarrow}{\infty} \nonumber\]
\[\text{as } x{\rightarrow}-{\infty}, \; f(x){\rightarrow}-{\infty} \nonumber\]
In words, we could say that as \(x\) values approach infinity, the function values approach infinity, and as \(x\) values approach negative infinity, the function values approach negative infinity.
We can tell this graph has the shape of an odd degree power function that has not been reflected, so the degree of the polynomial creating this graph must be odd and the leading coefficient must be positive.
Exercise \(\PageIndex{1}\)
Describe the end behavior, and determine a possible degree of the polynomial function in Figure \(\PageIndex{9}\).
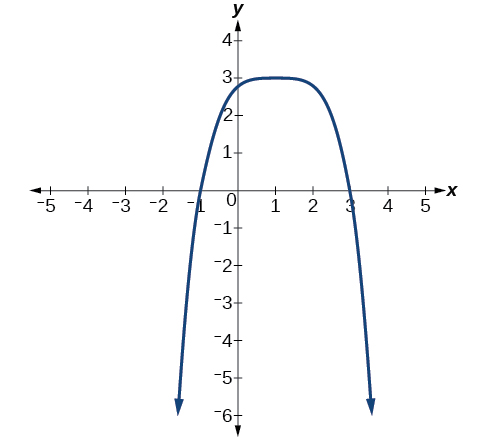
- Answer
-
As \(x{\rightarrow}{\infty}\), \(f(x){\rightarrow}−{\infty}\); as \(x{\rightarrow}−{\infty}\), \(f(x){\rightarrow}−{\infty}\). It has the shape of an even degree power function with a negative coefficient.
Example \(\PageIndex{7}\): Identifying End Behavior and Degree of a Polynomial Function
Given the function \(f(x)=−3x^2(x−1)(x+4)\), express the function as a polynomial in general form, and determine the leading term, degree, and end behavior of the function.
Solution
Obtain the general form by expanding the given expression for \(f(x)\).
\[\begin{align*} f(x)&=−3x^2(x−1)(x+4) \\ &=−3x^2(x^2+3x−4) \\ &=−3x^4−9x^3+12x^2 \end{align*}\]
The general form is \(f(x)=−3x^4−9x^3+12x^2\). The leading term is \(−3x^4\); therefore, the degree of the polynomial is 4. The degree is even (4) and the leading coefficient is negative (–3), so the end behavior is
\[\text{as }x{\rightarrow}−{\infty}, \; f(x){\rightarrow}−{\infty} \nonumber\]
\[\text{as } x{\rightarrow}{\infty}, \; f(x){\rightarrow}−{\infty} \nonumber\]
Exercise \(\PageIndex{7}\)
Given the function \(f(x)=0.2(x−2)(x+1)(x−5)\), express the function as a polynomial in general form and determine the leading term, degree, and end behavior of the function.
- Answer
-
The leading term is \(0.2x^3\), so it is a degree 3 polynomial. As \(x\) approaches positive infinity, \(f(x)\) increases without bound; as \(x\) approaches negative infinity, \(f(x)\) decreases without bound.
Identifying Local Behavior of Polynomial Functions
In addition to the end behavior of polynomial functions, we are also interested in what happens in the “middle” of the function. In particular, we are interested in locations where graph behavior changes. A turning point is a point at which the function values change from increasing to decreasing or decreasing to increasing.
We are also interested in the intercepts. As with all functions, the \(y\)-intercept is the point at which the graph intersects the vertical axis. The point corresponds to the coordinate pair in which the input value is zero. Because a polynomial is a function, only one output value corresponds to each input value so there can be only one \(y\)-intercept \((0,a_0)\). The \(x\)-intercepts occur at the input values that correspond to an output value of zero. It is possible to have more than one \(x\)-intercept. See Figure \(\PageIndex{10}\).
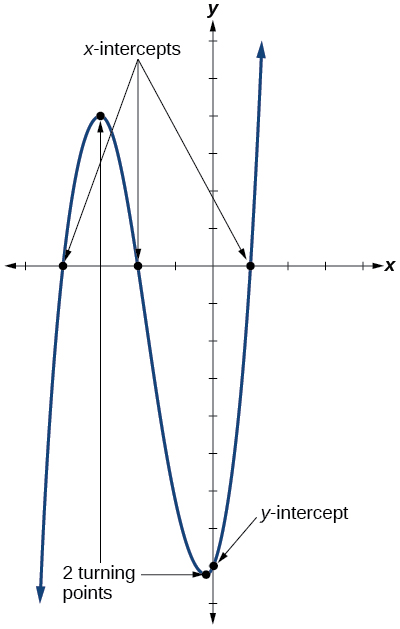
Defintion: Intercepts and Turning Points of Polynomial Functions
A turning point of a graph is a point at which the graph changes direction from increasing to decreasing or decreasing to increasing. The \(y\)-intercept is the point at which the function has an input value of zero. The \(x\)-intercepts are the points at which the output value is zero.
![]() Given a polynomial function, determine the intercepts.
Given a polynomial function, determine the intercepts.
- Determine the \(y\)-intercept by setting \(x=0\) and finding the corresponding output value.
- Determine the \(x\)-intercepts by solving for the input values that yield an output value of zero.
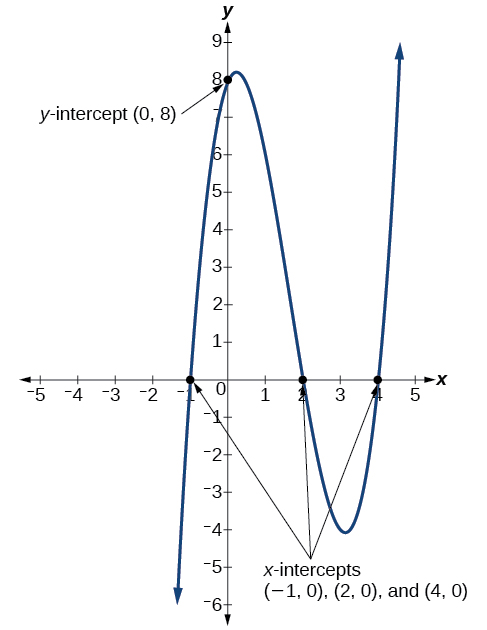
Example \(\PageIndex{8}\): Determining the Intercepts of a Polynomial Function
Given the polynomial function \(f(x)=(x−2)(x+1)(x−4)\), written in factored form for your convenience, determine the \(y\)- and \(x\)-intercepts.
Solution
The \(y\)-intercept occurs when the input is zero, so substitute 0 for \(x\).
\[ \begin{align*}f(0)&=(0−2)(0+1)(0−4) \\ &=(−2)(1)(−4) \\ &=8 \end{align*}\]
The \(y\)-intercept is \((0,8)\).
The \(x\)-intercepts occur when the output is zero.
\[ 0=(x−2)(x+1)(x−4) \nonumber \]
\[\begin{align*} x−2&=0 & &\text{or} & x+1&=0 & &\text{or} & x−4&=0 \\ x&=2 & &\text{or} & x&=−1 & &\text{or} & x&=4 \end{align*}\]
The \(x\)-intercepts are \((2,0)\),\((–1,0)\), and \((4,0)\).
We can see these intercepts on the graph of the function shown in Figure \(\PageIndex{11}\).
Example \(\PageIndex{9}\): Determining the Intercepts of a Polynomial Function with Factoring
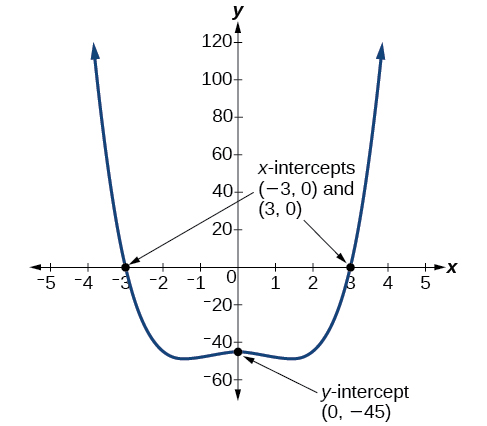
Given the polynomial function \(f(x)=x^4−4x^2−45\), determine the \(y\)- and \(x\)-intercepts.
Solution
The \(y\)-intercept occurs when the input is zero.
\[ \begin{align*} f(0) &=(0)^4−4(0)^2−45 \\[4pt] &=−45 \end{align*}\]
The \(y\)-intercept is \((0,−45)\).
The \(x\)-intercepts occur when the output is zero. To determine when the output is zero, we will need to factor the polynomial.
\[\begin{align*} f(x)&=x^4−4x^2−45 \\ &=(x^2−9)(x^2+5) \\ &=(x−3)(x+3)(x^2+5)
\end{align*}\]
\[0=(x−3)(x+3)(x^2+5) \nonumber\]
\[\begin{align*} x−3&=0 & &\text{or} & x+3&=0 & &\text{or} & x^2+5&=0 \\ x&=3 & &\text{or} & x&=−3 & &\text{or} &\text{(no real solution)} \end{align*}\]
The \(x\)-intercepts are \((3,0)\) and \((–3,0)\).
We can see these intercepts on the graph of the function shown in Figure \(\PageIndex{12}\). We can see that the function is even because \(f(x)=f(−x)\).
Exercise \(\PageIndex{5}\)
\(\PageIndex{5}\): Given the polynomial function \(f(x)=2x^3−6x^2−20x\), determine the \(y\)- and \(x\)-intercepts.
- Solution
-
\(y\)-intercept \((0,0)\); \(x\)-intercepts \((0,0)\),\((–2,0)\), and \((5,0)\)
Comparing Smooth and Continuous Graphs
The degree of a polynomial function helps us to determine the number of \(x\)-intercepts and the number of turning points. A polynomial function of \(n^\text{th}\) degree is the product of \(n\) factors, so it will have at most \(n\) roots or zeros, or \(x\)-intercepts. The graph of the polynomial function of degree \(n\) must have at most \(n–1\) turning points. This means the graph has at most one fewer turning point than the degree of the polynomial or one fewer than the number of factors.
A continuous function has no breaks in its graph: the graph can be drawn without lifting the pen from the paper. A smooth curve is a graph that has no sharp corners. The turning points of a smooth graph must always occur at rounded curves. The graphs of polynomial functions are both continuous and smooth.
Intercepts and Turning Points of Polynomials
A polynomial of degree \(n\) will have, at most, \(n\) \(x\)-intercepts and \(n−1\) turning points.
Example \(\PageIndex{10}\): Determining the Number of Intercepts and Turning Points of a Polynomial
Without graphing the function, determine the local behavior of the function by finding the maximum number of \(x\)-intercepts and turning points for \(f(x)=−3x^{10}+4x^7−x^4+2x^3\).
Solution
The polynomial has a degree of 10, so there are at most \(n\) \(x\)-intercepts and at most \(n−1\) turning points.
Exercise \(\PageIndex{6}\)
Without graphing the function, determine the maximum number of \(x\)-intercepts and turning points for \(f(x)=108−13x^9−8x^4+14x^{12}+2x^3\)
- Answer
-
There are at most 12 \(x\)-intercepts and at most 11 turning points.
Example \(\PageIndex{11}\): Drawing Conclusions about a Polynomial Function from the Graph
What can we conclude about the polynomial represented by the graph shown in Figure \(\PageIndex{12}\) based on its intercepts and turning points?
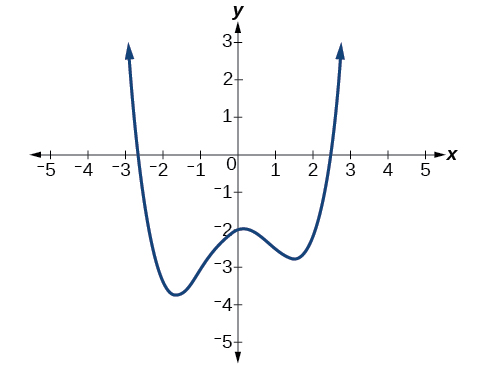
Solution
The end behavior of the graph tells us this is the graph of an even-degree polynomial. See Figure \(\PageIndex{14}\).
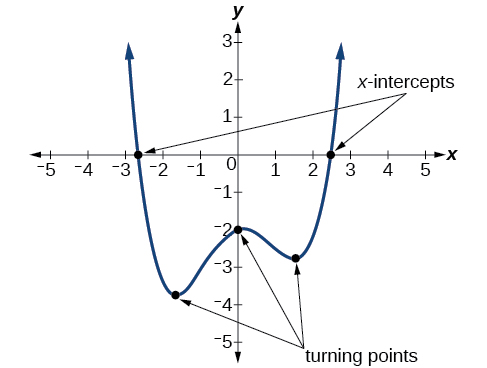
The graph has 2 \(x\)-intercepts, suggesting a degree of 2 or greater, and 3 turning points, suggesting a degree of 4 or greater. Based on this, it would be reasonable to conclude that the degree is even and at least 4.
Exercise \(\PageIndex{7}\)
What can we conclude about the polynomial represented by the graph shown in Figure \(\PageIndex{15}\) based on its intercepts and turning points?
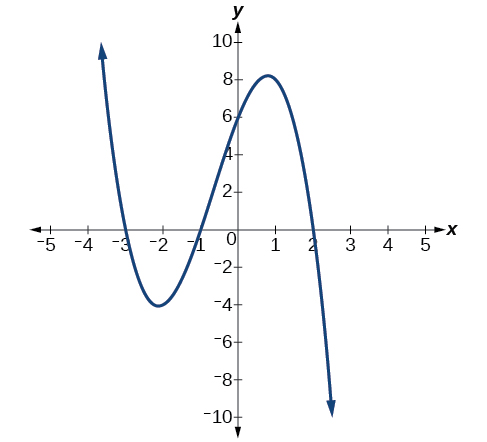
Figure \(\PageIndex{15}\).
- Answer
-
Add texts here. Do not delete this text first.
Solution
The end behavior indicates an odd-degree polynomial function; there are 3 \(x\)-intercepts and 2 turning points, so the degree is odd and at least 3. Because of the end behavior, we know that the lead coefficient must be negative.
Example \(\PageIndex{12}\): Drawing Conclusions about a Polynomial Function from the Factors
Given the function \(f(x)=−4x(x+3)(x−4)\), determine the local behavior.
Solution
The \(y\)-intercept is found by evaluating \(f(0)\).
\[\begin{align*} f(0)&=−4(0)(0+3)(0−4) \\ &=0 \end{align*}\]
The \(y\)-intercept is \((0,0)\).
The \(x\)-intercepts are found by determining the zeros of the function.
\[\begin{align*} 0&=-4x(x+3)(x-4) \\ x&=0 & &\text{or} & x+3&=0 & &\text{or} & x-4&=0 \\ x&=0 & &\text{or} & x&=−3 & &\text{or} & x&=4 \end{align*}\]
The \(x\)-intercepts are \((0,0)\),\((–3,0)\), and \((4,0)\).
The degree is 3 so the graph has at most 2 turning points.
Exercise \(\PageIndex{8}\)
Given the function \(f(x)=0.2(x−2)(x+1)(x−5)\), determine the local behavior.
- Answer
-
The \(x\)-intercepts are \((2,0)\), \((−1,0)\), and \((5,0)\), the \(y\)-intercept is \((0,2)\), and the graph has at most 2 turning points.
Key Equations
- general form of a polynomial function: \(f(x)=a_nx^n+a_{n-1}x^{n-1}...+a_2x^2+a_1x+a_0\)
Key Concepts
- A power function is a variable base raised to a number power.
- The behavior of a graph as the input decreases without bound and increases without bound is called the end behavior.
- The end behavior depends on whether the power is even or odd.
- A polynomial function is the sum of terms, each of which consists of a transformed power function with positive whole number power.
- The degree of a polynomial function is the highest power of the variable that occurs in a polynomial. The term containing the highest power of the variable is called the leading term. The coefficient of the leading term is called the leading coefficient.
- The end behavior of a polynomial function is the same as the end behavior of the power function represented by the leading term of the function.
- A polynomial of degree \(n\) will have at most \(n\) \(x\)-intercepts and at most \(n−1\) turning points.
Glossary
coefficient
a nonzero real number that is multiplied by a variable raised to an exponent (only the number factor is the coefficient)
continuous function
a function whose graph can be drawn without lifting the pen from the paper because there are no breaks in the graph
degree
the highest power of the variable that occurs in a polynomial
end behavior
the behavior of the graph of a function as the input decreases without bound and increases without bound
leading coefficient
the coefficient of the leading term
leading term
the term containing the highest power of the variable
polynomial function
a function that consists of either zero or the sum of a finite number of non-zero terms, each of which is a product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.
power function
a function that can be represented in the form \(f(x)=kx^p\) where \(k\) is a constant, the base is a variable, and the exponent, \(p\), is a constant
smooth curve
a graph with no sharp corners
term of a polynomial function
any \(a_ix^i\) of a polynomial function in the form \(f(x)=a_nx^n+a_{n-1}x^{n-1}...+a_2x^2+a_1x+a_0\)
turning point
the location at which the graph of a function changes direction


