8.R: Further Applications of Trigonometry (Review)

Last updated
Save as PDF

Page ID: 18807

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

8.1: Non-right Triangles: Law of Sines

For the exercises 1-5 assume $\alpha $ is opposite side $a$, $\beta $ is opposite side $b$, and $\gamma $ is opposite side $c$. Solve each triangle, if possible. Round each answer to the nearest tenth.

1) $\beta =50^{\circ}, a=105, b=45$

Answer: Not possible

2) $\alpha =43.1^{\circ}, a=184.2, b=242.8$

3) Solve the triangle.

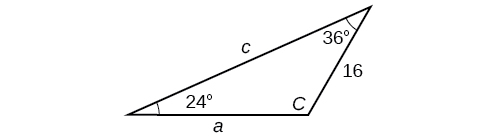
$Ex 8R 8.1.3.png$

Answer: $C=120^{\circ}, a=23.1, c=34.1$

4) Find the area of the triangle.

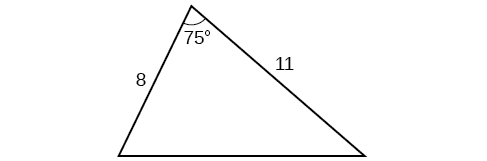
5) A pilot is flying over a straight Highway. He determines the angles of depression to two mile posts $2.1$ km apart to be $25^{\circ}$ and $49^{\circ}$, as shown in the figure below. Find the distance of the plane from point $A$ and the elevation of the plane.

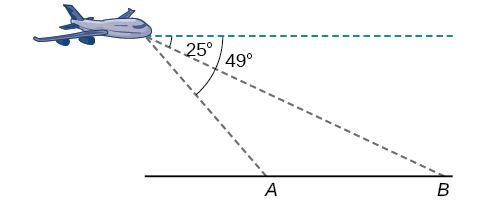
$Ex 8R 8.1.5.png$

Answer: distance of the plane from point $A:2.2$ km, elevation of the plane: $1.6$ km

8.2: Non-right Triangles - Law of Cosines

1) Solve the triangle, rounding to the nearest tenth, assuming $\alpha $ is opposite side $a$, $\beta $ is opposite side $b$, and $\gamma $ s opposite side $c: a=4, b=6,c=8$.

2) Solve the triangle in the Figure below, rounding to the nearest tenth.

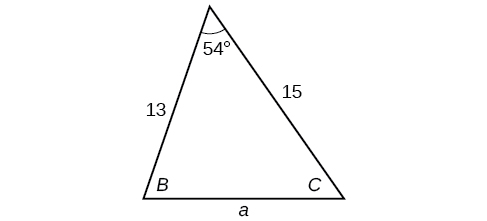
$Ex 8R 8.2.2.png$

Answer: $B=71.0^{\circ},C=55.0^{\circ},a=12.8$

3) Find the area of a triangle with sides of length $8.3$, $6.6$, and $9.1$.

4) To find the distance between two cities, a satellite calculates the distances and angle shown in the Figure below (not to scale). Find the distance between the cities. Round answers to the nearest tenth.

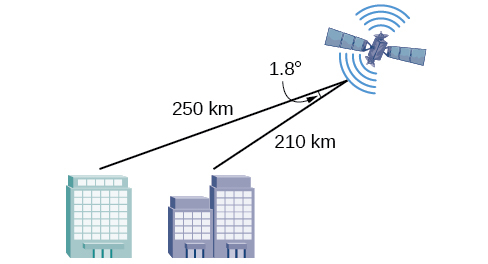
$Ex 8R 8.2.4.png$

Answer: $40.6$ km

8.3: Polar Coordinates

1) Plot the point with polar coordinates $\left ( 3,\dfrac{\pi }{6} \right )$.

2) Plot the point with polar coordinates $\left ( 5,\dfrac{-2\pi }{3} \right )$.

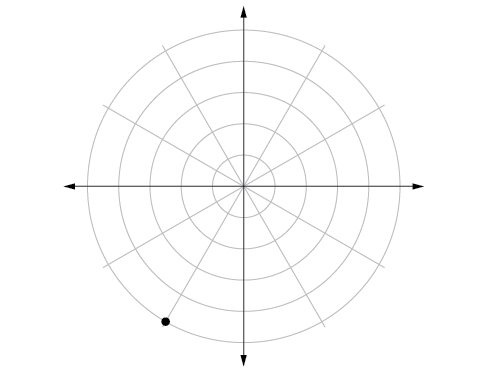
Answer: $Ex 8R 8.3.2.png$

3) Convert $\left ( 6,\dfrac{-3\pi }{4} \right )$ to rectangular coordinates.

4) Convert $\left ( -2,\dfrac{3\pi }{2} \right )$ to rectangular coordinates.

Answer: $(0,2)$

5) Convert $(7,-2)$ to polar coordinates.

6) Convert $(-9,-4)$ to polar coordinates.

Answer: $(9.8489,203.96^{\circ})$

For the exercises 7-9, convert the given Cartesian equation to a polar equation.

7) $x=-2$

8) $x^2+y^2=64$

Answer: $r=8$

9) $x^2+y^2=-2y$

For the exercises 10-11, convert the given polar equation to a Cartesian equation.

10) $r=7\cos \theta$

Answer: $x^2+y^2=7x$

11) $r=\dfrac{-2}{4\cos \theta +\sin \theta }$

For the exercises 12-13, convert to rectangular form and graph.

12) $\theta =\dfrac{3\pi }{4}$

Answer

$y=-x$

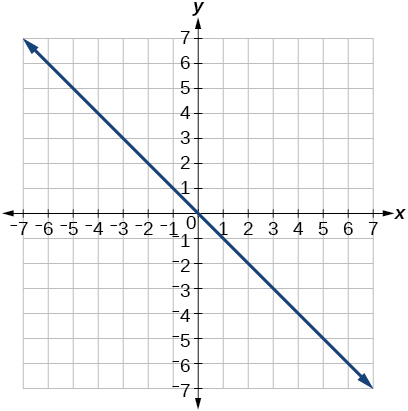
$Ex 8R 8.3.12.png$

13) $r=5\sec \theta$

8.4: Polar Coordinates - Graphs

For the exercises 1-5, test each equation for symmetry.

1) $r=4+4\sin \theta$

Answer: symmetric with respect to the line $\theta =\dfrac{\pi }{2}$

2) $r=7$

3) Sketch a graph of the polar equation $r=1-5\sin \theta$. Label the axis intercepts.

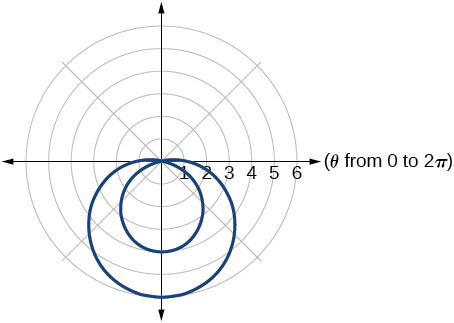
Answer: $Ex 8R 8.4.3.png$

4) Sketch a graph of the polar equation $r=5\sin (7\theta )$.

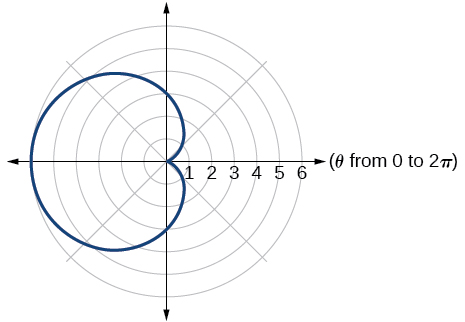
5) Sketch a graph of the polar equation $r=3-3\cos \theta$

Answer: $Ex 8R 8.4.5.png$

8.5: Polar Form of Complex Numbers

For the exercises 1-2, find the absolute value of each complex number.

1) $-2+6i$

2) $4-3i$

Answer: $5$

Write the complex number in polar form.

3) $5+9i$

4) $\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i$

Answer: $\mathrm{cis}\left (-\dfrac{\pi }{3} \right )$

For the exercises 5-6, convert the complex number from polar to rectangular form.

5) $z=5\mathrm{cis}\left (\dfrac{5\pi }{6} \right )$

6) $z=3\mathrm{cis}(40^{\circ})$

Answer: $2.3+1.9i$

For the exercises 7-8, find the product $z_1 z_2$ in polar form.

7) $\begin{align*} z_1 &= 2\mathrm{cis}(89^{\circ})\\ z_2 &= 5\mathrm{cis}(23^{\circ}) \end{align*}$

8) $\begin{align*} z_1 &= 10\mathrm{cis}\left ( \dfrac{\pi }{6} \right )\\ z_2 &= 6\mathrm{cis}\left ( \dfrac{\pi }{3} \right ) \end{align*}$

Answer: $60\mathrm{cis}\left ( \dfrac{\pi }{2} \right )$

For the exercises 9-10, find the quotient $\dfrac{z_1}{z_2}$ in polar form.

9) $\begin{align*} z_1 &= 12\mathrm{cis}(55^{\circ})\\ z_2 &= 3\mathrm{cis}(18^{\circ}) \end{align*}$

10) $\begin{align*} z_1 &= 27\mathrm{cis}\left ( \dfrac{5\pi }{3} \right )\\ z_2 &= 9\mathrm{cis}\left ( \dfrac{\pi }{3} \right ) \end{align*}$

Answer: $3\mathrm{cis}\left ( \dfrac{4\pi }{3} \right )$

For the exercises 11-12, find the powers of each complex number in polar form.

11) Find $z^4$ when $z=2\mathrm{cis}(70^{\circ})$

12) Find $z^2$ when $z=5\mathrm{cis}\left ( \dfrac{3\pi }{4} \right )$

Answer: $25\mathrm{cis}\left ( \dfrac{3\pi }{2} \right )$

For the exercises 13-14, evaluate each root.

13) Evaluate the cube root of $z$ when $z=64\mathrm{cis}(210^{\circ})$.

14) Evaluate the square root of $z$ when $z=25\mathrm{cis}\left ( \dfrac{3\pi }{2} \right )$.

Answer: $5\mathrm{cis}\left ( \dfrac{3\pi }{4} \right )$, $5\mathrm{cis}\left ( \dfrac{7\pi }{4} \right )$

For the exercises 15-16, plot the complex number in the complex plane.

15) $6-2i$

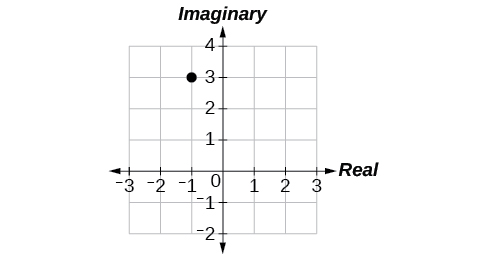
16) $-1+3i$

Answer: $Ex 8R 8.5.16.png$

8.6: Parametric Equations

1) $\begin{cases} & x(t)= 3t-1\\ & y(t)= \sqrt{t} \end{cases}$

2) $\begin{cases} & x(t)= -\cos t\\ & y(t)= 2\sin ^2t \end{cases}$

Answer: $x^2+\dfrac{1}{2}y=1$

3) Parameterize (write a parametric equation for) each Cartesian equation by using $x(t)=a\cos t$ and $y(t)=b\sin t$ for $\dfrac{x^2}{25}+\dfrac{y^2}{16}=1$.

4) Parameterize the line from $(-2,3)$ to $(4,7)$ so that the line is at $(-2,3)$ at $t=0$ and $(4,7)$ at $t=1$.

Answer: $\begin{cases} & x(t)= -2+6t\\ & y(t)= 3+4t \end{cases}$

8.7: Parametric Equations - Graphs

For the exercises 1-, make a table of values for each set of parametric equations, graph the equations, and include an orientation; then write the Cartesian equation.

1) $\begin{cases} & x(t)= 3t^2\\ & y(t)= 2t-1 \end{cases}$

2) $\begin{cases} & x(t)= e^t\\ & y(t)= -2e^{5t} \end{cases}$

Answer

$y=-2x^5$

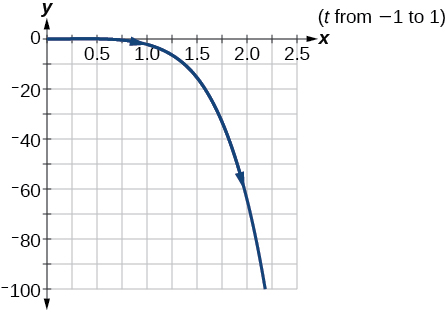
$Ex 8R 8.7.2.png$

3) $\begin{cases} & x(t)= 3\cos t\\ & y(t)= 2\sin t \end{cases}$

4) A ball is launched with an initial velocity of $80$ feet per second at an angle of $40^{\circ}$ to the horizontal. The ball is released at a height of $4$ feet above the ground.

Where is the ball after $3$ seconds?
How long is the ball in the air?

Answer

$\begin{cases} & x(t)= (80\cos (40^{\circ}))t\\ & y(t)= -16t^2+(80\sin (40^{\circ}))t+4 \end{cases}$
The ball is 14 feet high and 184 feet from where it was launched.
$3.3$ seconds

8.8: Vectors

For the exercises 1-2, determine whether the two vectors, $\vecs u$ and $\vecs v$, are equal, where $\vecs u$ has an initial point $P_1$ and a terminal point $P_2$, and $\vecs v$ has an initial point $P_3$ and a terminal point $P_4$.

1) $P_1=(-1,4), P_2=(3,1), P_3=(5,5), P_4=(9,2)$

2) $P_1=(6,11), P_2=(-2,8), P_3=(0,-1), P_4=(-8,2)$

Answer: not equal

For the exercises 3-4, use the vectors $\vecs u=2\hat{\mathbf{i}}-\hat{\mathbf{j}}$, $\vecs v=4\hat{\mathbf{i}}-3\hat{\mathbf{j}}$, and $\vecs w=-2\hat{\mathbf{i}}+5\hat{\mathbf{j}}$ to evaluate the expression.

3) $ \vecs u-\vecs v $

4) $ 2\vecs v-\vecs u+\vecs w $

Answer: $4\hat{\mathbf{i}}$

For the exercises 5-6, find a unit vector in the same direction as the given vector.

5) $\vecs a=8\hat{\mathbf{i}}-6\hat{\mathbf{j}}$

6) $\vecs b=-3\hat{\mathbf{i}}-\hat{\mathbf{j}}$

Answer: $-\dfrac{3\sqrt{10}}{10}\hat{\mathbf{i}}-\dfrac{\sqrt{10}}{10}\hat{\mathbf{j}}$

For the exercises 7-11, calculate $\vecs u\cdot \vecs v$

7) $\vecs u=-2\hat{\mathbf{i}}+\hat{\mathbf{j}}$ and $\vecs v=3\hat{\mathbf{i}}+7\hat{\mathbf{j}}$

8) $\vecs u=\hat{\mathbf{i}}+4\hat{\mathbf{j}}$ and $\vecs v=4\hat{\mathbf{i}}+3\hat{\mathbf{j}}$

Answer: $16$

9) Given $\vecs v=\left \langle -3,4 \right \rangle$ draw $\vecs v$, $2\vecs v$, and $\dfrac{1}{2}\vecs v$ .

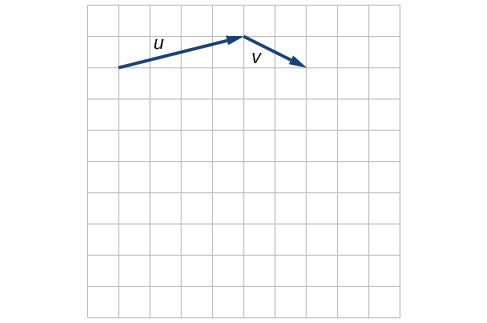
10) Given the vectors shown in the Figure below, sketch $\vecs u + \vecs v$, $\vecs u − \vecs v$ and $3\vecs v$ .

$Ex 8R 8.8.10.png$

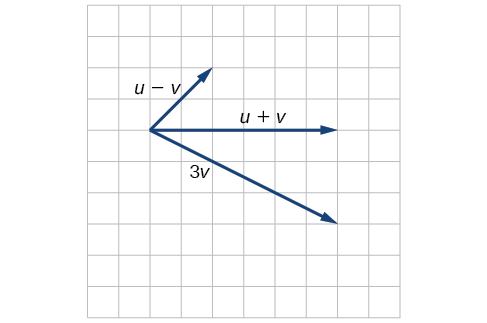
Answer: $Ex 8R 8.8.10 sol.png$

11) Given initial point $P_1=(3,2)$ and terminal point $P_2=(-5,-1)$, write the vector $\vecs v$ in terms of $\hat{\mathbf{i}}$ and $\hat{\mathbf{j}}$. Draw the points and the vector on the graph.

Practice Test

1) Assume $\alpha $ is opposite side $a$, $\beta $ is opposite side $b$, and $\gamma $ is opposite side $c$. Solve the triangle, if possible, and round each answer to the nearest tenth, given $\beta =68^{\circ},b=21,c=16$.

Answer: $\alpha =67.1^{\circ}, \gamma =44.9^{\circ}, a=20.9$

2) Find the area of the triangle in the Figure below. Round each answer to the nearest tenth.

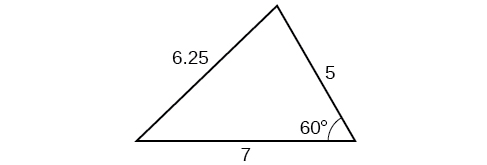
$Ex 8RP.2.png$

3) A pilot flies in a straight path for $2$ hours. He then makes a course correction, heading $15^{\circ}$ to the right of his original course, and flies $1$ hour in the new direction. If he maintains a constant speed of $575$ miles per hour, how far is he from his starting position?

Answer: $1712$ miles

4) Convert $(2,2)$ to polar coordinates, and then plot the point.

5) Convert $\left ( 2,\dfrac{\pi }{3} \right )$ to rectangular coordinates.

Answer: $(1,\sqrt{3})$

6) Convert the polar equation to a Cartesian equation: $x^2+y^2=5y$.

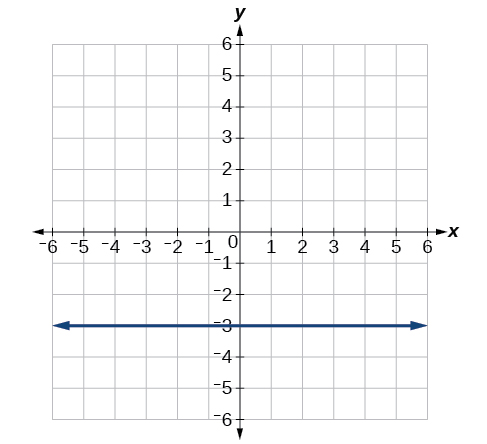
7) Convert to rectangular form and graph:$r=-3\csc θ$.

Answer

$y=-3$

$Ex 8RP.7.png$

8) Test the equation for symmetry: $r=-4\sin(2\theta )$.

9) Graph $r=3+3\cos \theta$.

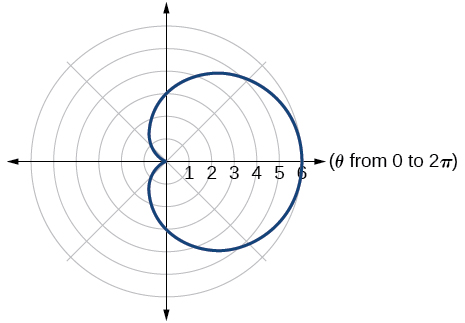
Answer: $Ex 8RP.9.png$

10) Graph $r=3-5\sin \theta$.

11) Find the absolute value of the complex number $5-9i$.

Answer: $\sqrt{106}$

12) Write the complex number in polar form: $4+i$.

13) Convert the complex number from polar to rectangular form: $z=5\mathrm{cis}\left ( \dfrac{2\pi }{3} \right )$

Answer: $\dfrac{-5}{2}+i\dfrac{5\sqrt{3}}{2}$

14) $z_1 z_2$

15) $\dfrac{z_1}{z_2}$

Answer: $4\mathrm{cis}(21^{\circ})$

16) $(z_2)^3$

17) $\sqrt{z_1}$

Answer: $2\sqrt{2}\mathrm{cis}(18^{\circ}), 2\sqrt{2}\mathrm{cis}(198^{\circ})$

18) Plot the complex number $-5-i$ in the complex plane.

19) Eliminate the parameter $t$ to rewrite the following parametric equations as a Cartesian equation: $\begin{cases} & x(t)= t+1\\ & y(t)= 2t^2 \end{cases}$

Answer: $y=2(x-1)^2$

20) Parameterize (write a parametric equation for) the following Cartesian equation by using $x(t)=a\cos t$ and $y(t)=b\sin t : \dfrac{x^2}{36}+\dfrac{y^2}{100}=1$

21) Graph the set of parametric equations and find the Cartesian equation: $\begin{cases} & x(t)= -2\sin t\\ & y(t)= 5\cos t \end{cases}$

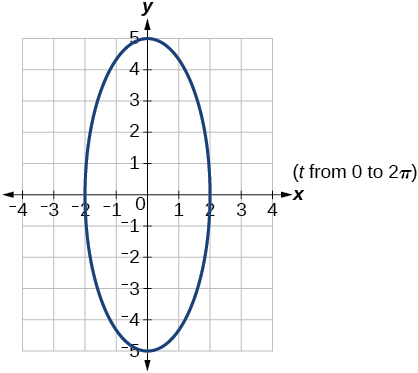
Answer: $Ex 8RP.21.png$

22) A ball is launched with an initial velocity of $95$ feet per second at an angle of $52^{\circ}$ to the horizontal. The ball is released at a height of $3.5$ feet above the ground.

Where is the ball after $2$ seconds?
How long is the ball in the air?

For the exercises 23-26, use the vectors $\vecs u = \hat{\mathbf{i}} − 3\hat{\mathbf{j}}$ and $\vecs v = 2\hat{\mathbf{i}} + 3\hat{\mathbf{j}}$.

23) Find $2\vecs u − 3\vecs v$ .

Answer: $-4\hat{\mathbf{i}}-15\hat{\mathbf{j}}$

24) Calculate $\vecs u\cdot \vecs v$ .

25) Find a unit vector in the same direction as $\vecs v$.

Answer: $\dfrac{2\sqrt{3}}{13}\hat{\mathbf{i}}+\dfrac{3\sqrt{3}}{13}\hat{\mathbf{j}}$

26) Given vector $\vecs v$ has an initial point $P_1=(2,2)$ and terminal point $P_2=(-1,0)$, write the vector $\vecs u\cdot \vecs v$ .

Contributors and Attributions

Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.

Search

Text Color

Text Size

Margin Size

Font Type