16.3: Role Algebra for Mulitplex Data
- Page ID
- 7749
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Let's suppose that we were looking at a single matrix on who was friends with whom. An obvious way of characterizing what we see is to classify each pair as "friends" or "not friends". But now, let's extend our analysis one step further (or look at paths of length 2). Now each pair of actors could be characterized as friend, not friend, friend of friend, friend of not-friend, not-friend of friend, or not-friend of not-friend. If we wanted to consider paths of length three...well, you get the idea.
The notion of a "role algebra" is to understand the relations between actors as realizations of the logically possible "compounds" of relations of selected path lengths. Most often in network analyses, we focus on path of length one (two actors are connected or not). But, sometimes it is useful to characterize a graph as containing more complex kinds of relations (friend of friend, not-friend of friend, etc.). Lists of these kinds of relations can be obtained by taking Boolean products of matrices (i.e. 0 * 0 = 0, 0 * 1 = 0, 1 * 0 = 0, and 1 * 1 = 1). When applied to single matrix, we raise a matrix to a power (multiply it by itself) and take the Boolean product; the result generates a matrix that tells us if there is a relation between each pair of nodes that is of a path length equal to the power. That is, to find whether each pair of actors is connected by the relation "friend of a friend" we take the Boolean product of the friendship matrix squared.
This (elegant, but rather mysterious) method of finding "compound relations" can be applied to multiplex data as a way of identifying the kinds of relations that exist in a multiplex graph. The Transform>Semigroup algorithm can be used to identify these more complex qualitative kinds of relations among nodes.
It is easier for most people to understand this with an example, than in the abstract. So let's do a somewhat extended examination of the Knoke data for both information and money ties.
If we consider just direct relations, there are two: organizations can be tied by information; organizations can be tied by money. What if we consider relations at two steps (what are called "word lengths" in role algebra)? In addition to the original two relations, there are now four more:
- When we multiply the information matrix by its transpose and take Boolean products, we are identifying linkages like "sends information to a node that send information to..."
- When we multiply the money matrix by its transpose and take Boolean products, we are identifying the linkage: "sends money to a node that send money to..."
- When we multiply the information matrix by the money matrix, we are identifying the relationship: "sends information to a node that sends money to..."
- When we multiply the money matrix by the information matrix, we are identifying the relationship: "sends money to a node that sends information to..."
These four new (two-step) relations among nodes are "words" of length two, or "compounds".
It is possible, of course, to continue to compound to still greater lengths. In most sociological analyses with only two types of ties, longer lengths are rarely substantively meaningful. With more kinds of ties, however, the number of types of compound relationships can become quite large quite quickly.
The tool Transform>Semigroup computes all of the logically possible compounded types of relations up to a word length (i.e. network distance) that the user specifies. It produces a log file that contains a "map" of the types of relations, as we see in Figure 16.9. It also produces, in a separate file, adjacency matrices for each of the types of relationships (Figures 16.10 and 16.11).
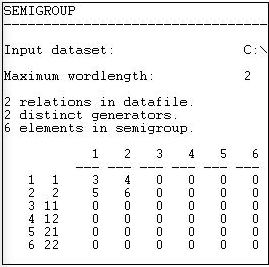
Figure 16.9: Semigroups of word-length 2 for Knoke information and money networks
The output tells us that there were two relations (information and money). These were the "generators" that were used to create the types. Six possible compound relations were generated for the word-length 2 (identified down the left-hand side). Relations 1 and 2 are information and money individually - the original matrices. Relation 3 is a compound of information with itself; relation four is the compound of information with money, etc. The numbers (3, 4, 5, 6) are simply guides to which matrix in the output file refers to which relation.
From these new "types" of relations (which are compounds within and between the two types of ties) we can generate new adjacency matrices that show which pairs of actors are joined by each particular type of relation. These are presented as a series of adjacency matrices, as shown in Figure 16.10 and continued in Figure 16.11.

Figure 16.10: Relations tables for Figure 16.9 (part 1)
Matrix 1 is simply the original information matrix; matrix 2 is the original money matrix. Matrix 3 is the compound of information with information - which actors are tied by a relationship "Ego sends information to someone who sends information to Alter"?

Figure 16.11: Relations tables for Figure 16.9 (part 2)
Matrix 4 is the compound of money with itself, or "Ego sends money to someone who sends money to Alter".
Matrices 5 and 6 are, in some ways, the most interesting. While exchanging information for information and money for money are obvious ways in which a network can be integrated, it is also possible that actors can be integrated by relations that involve both "apples" and "oranges". That is, I may send money, and receive information; I may send information, and receive money.
Role algebra has proven to be of particular value in the study of kinship relations, where across-generation (parent/child) ties are recorded in one matrix and within-generation relations are recorded in another. The various compounds (e.g. "child of child", "child of brother") fairly easily capture the meaningful terms in kinship relations.


