4.8: Parabollic fixed points and Siegel disk

Last updated
Save as PDF

Page ID: 102232

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

If multiplicator of a fixed point satisfies |λ| ≠ 1 then dynamics in its vicinity is simple attraction or repelling. It is much more complex for |λ| = 1.

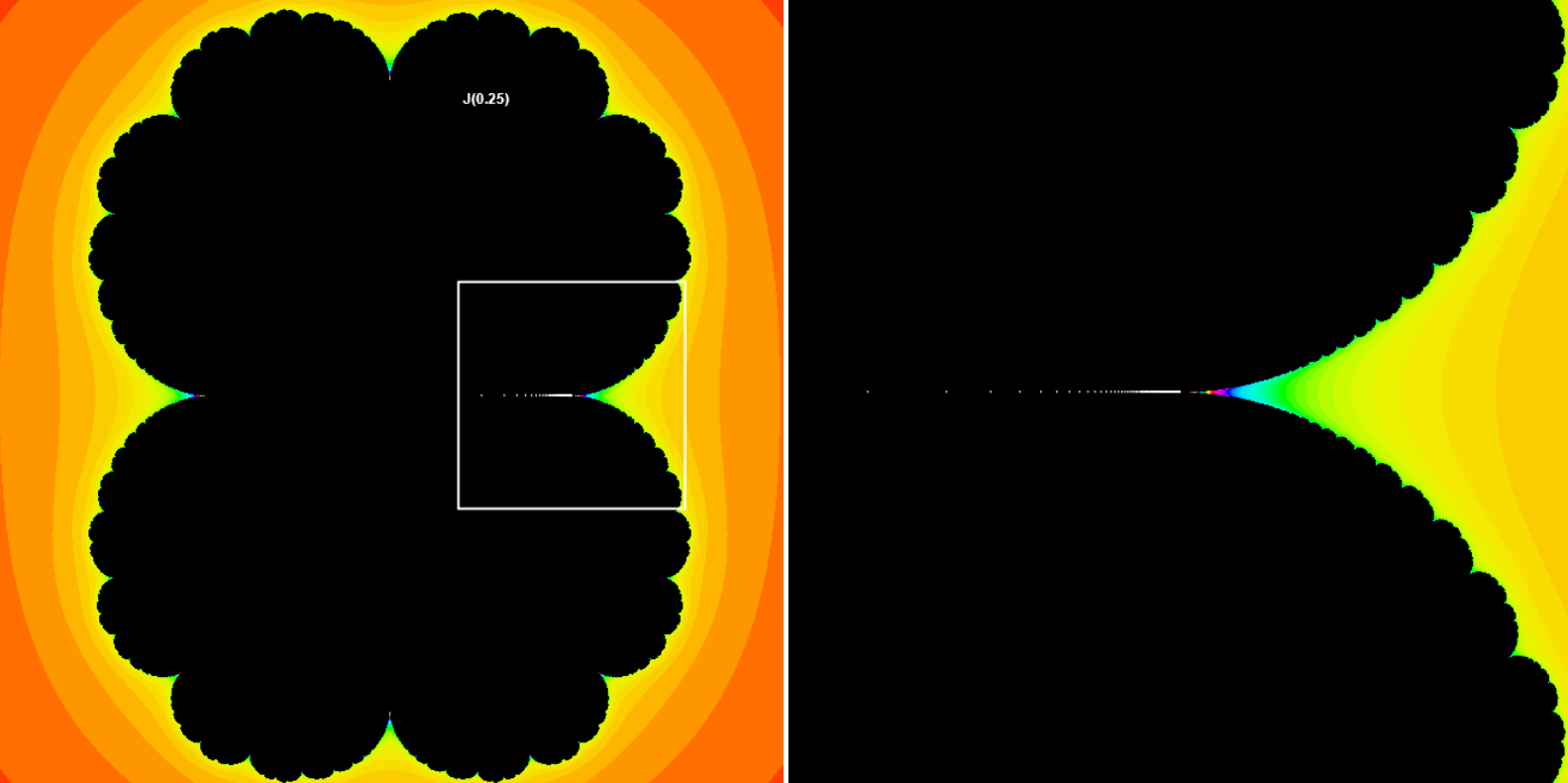
For λⁿ = 1 (i.e. λ = e^{2π i m/n} where m, n are integer), the fixed poit is called parabollic. E.g. as we have seen before, for c → 1/4 attracting and repelling fixed points merge together and make parabollic fixed point with multiplicator λ = 1 (in the center of the white square below). The point has one attracting and one repellinga directions. You can see that white points of the orbit starting at z = 0 are attracted to this parabollic point. Points to the right from the fixed point go to infinity.

Parabollic point with 3 attracting and repelling directions is shown below.

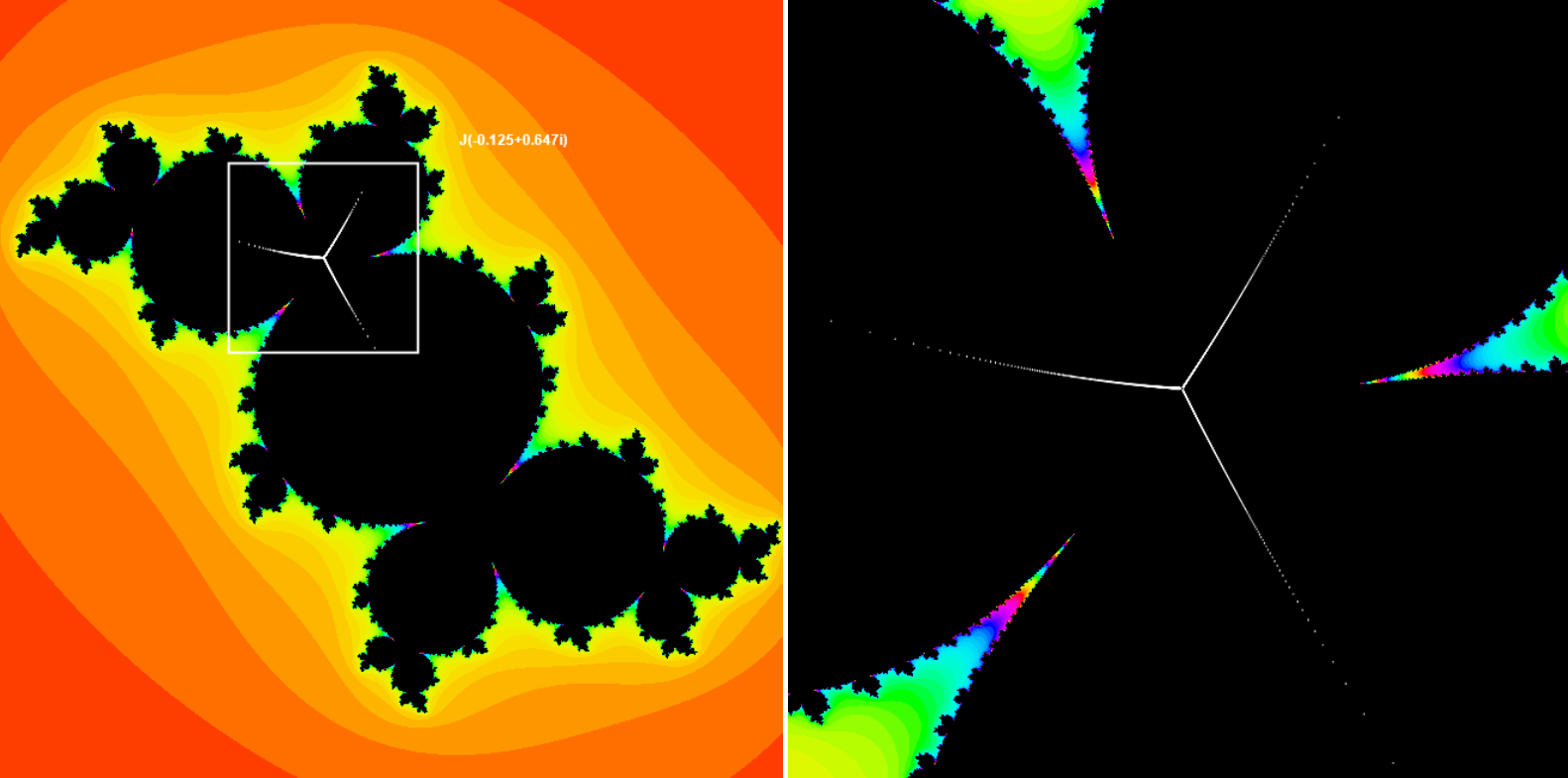
If λ = e^{2π i x} (where x is real irrational number) then in vicinity of fixed point for "almost all" x the mapping is equivalent to rotation by 2π x angle. For some x values the map is not equivalent to rotation. These fixed points are called Cremer points. It is impossible to use irrational numbers on computers but mathematitiens have strong proof that Siegel and Cremer points exist.

To the left you see that orbit starting at z = -0.2 + 0.2i rotates around fixed point. It is very likely that we have Siegel disk for this C value (at least for 1500 iterations :)