2.4E: Exercises
- Page ID
- 32406
Practice Makes Perfect
Solve a Formula for a Specific Variable
In the following exercises, solve the given formula for the specified variable.
Solve the formula \(C=πd\) for d.
- Answer
-
\(d=\frac{C}{π}\)
Solve the formula \(C=πd\) for \(π\).
Solve the formula \(V=LWH\) for L.
- Answer
-
\(L=\frac{V}{WH}\)
Solve the formula \(V=LWH\) for H.
Solve the formula \(A=\frac{1}{2}bh\) for b.
- Answer
-
\(b=\frac{2A}{h}\)
Solve the formula \(A=\frac{1}{2}bh\) for h.
Solve the formula
\(A=\frac{1}{2}d_1d_2\) for \(d_1\).
- Answer
-
\(d_1=\frac{2A}{d_2}\)
Solve the formula
\(A=\frac{1}{2}d_1d_2\) for \(d_2.\)
Solve the formula
\(A=\frac{1}{2}h(b_1+b_2)\) for \(b_1\).
- Answer
-
\(b_1=\frac{2A}{h}−b_2\)
Solve the formula
\(A=\frac{1}{2}h(b_1+b_2)\) for \(b_2\).
Solve the formula
\(h=54t+\frac{1}{2}at^2\) for a.
- Answer
-
\(a=\frac{2h−108t}{t^2}\)
Solve the formula
\(h=48t+\frac{1}{2}at^2\) for a.
Solve \(180=a+b+c\) for a.
- Answer
-
\(a=180−b−c\)
Solve \(180=a+b+c\) for c.
Solve the formula
\(A=\frac{1}{2}pl+B\) for p.
- Answer
-
\(p=\frac{2A−2B}{l}\)
Solve the formula
\(A=\frac{1}{2}pl+B\) for l.
Solve the formula
\(P=2L+2W\) for L.
- Answer
-
\(L=\frac{P−2W}{2}\)
Solve the formula
\(P=2L+2W\) for W.
In the following exercises, solve for the formula for y.
Solve the formula
\(8x+y=15\) for y.
- Answer
-
\(y=15−8x\)
Solve the formula
\(9x+y=13\) for y.
Solve the formula
\(−4x+y=−6\) for y.
- Answer
-
\(y=−6+4x\)
Solve the formula
\(−5x+y=−1\) for y.
Solve the formula
\(x−y=−4\) for y.
- Answer
-
\(y=4+x\)
Solve the formula
\(x−y=−3\) for y.
Solve the formula
\(4x+3y=7\) for y.
- Answer
-
\(y=\frac{7−4x}{3}\)
Solve the formula
\(3x+2y=11\) for y.
Solve the formula
\(2x+3y=12\) for y
- Answer
-
\(y=\frac{12−2x}{3}\)
Solve the formula
\(5x+2y=10\) for y.
Solve the formula
\(3x−2y=18\) for y.
- Answer
-
\(y=\frac{18−3x}{−2}\)
Solve the formula
\(4x−3y=12\) for y.
Use Formulas to Solve Geometry Applications
In the following exercises, solve using a geometry formula.
A triangular flag has area 0.75 square feet and height 1.5 foot. What is its base?
- Answer
-
1 foot
A triangular window has area 24 square feet and height six feet. What is its base?
What is the base of a triangle with area 207 square inches and height 18 inches?
- Answer
-
23 inches
What is the height of a triangle with area 893 square inches and base 38 inches?
The two smaller angles of a right triangle have equal measures. Find the measures of all three angles.
- Answer
-
\(45°,45°,90°\)
The measure of the smallest angle of a right triangle is \(20°\) less than the measure of the next larger angle. Find the measures of all three angles.
The angles in a triangle are such that one angle is twice the smallest angle, while the third angle is three times as large as the smallest angle. Find the measures of all three angles.
- Answer
-
\(30°,60°,90°\)
The angles in a triangle are such that one angle is 20 more than the smallest angle, while the third angle is three times as large as the smallest angle. Find the measures of all three angles.
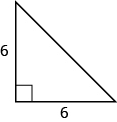
In the following exercises, use the Pythagorean Theorem to find the length of the hypotenuse.
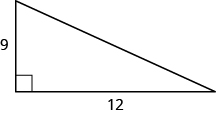
- Answer
-
15
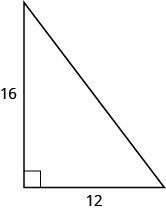
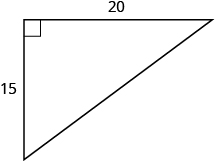
- Answer
-
25
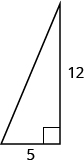
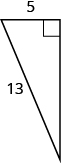
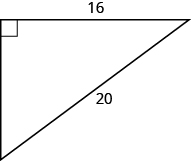
In the following exercises, use the Pythagorean Theorem to find the length of the leg. Round to the nearest tenth if necessary.
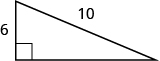
- Answer
-
8
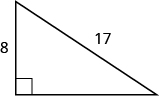
- Answer
-
12
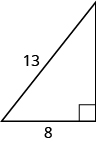
- Answer
-
10.2
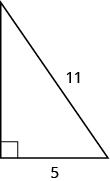
- Answer
-
9.8
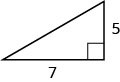
In the following exercises, solve using a geometry formula.
The width of a rectangle is seven meters less than the length. The perimeter is 58 meters. Find the length and width.
- Answer
-
18 meters, 11 meters
The length of a rectangle is eight feet more than the width. The perimeter is 60 feet. Find the length and width.
The width of the rectangle is 0.7 meters less than the length. The perimeter of a rectangle is 52.6 meters. Find the dimensions of the rectangle.
- Answer
-
\(13.5\) m, \(12.8\) m
The length of the rectangle is 1.1 meters less than the width. The perimeter of a rectangle is 49.4 meters. Find the dimensions of the rectangle.
The perimeter of a rectangle of 150 feet. The length of the rectangle is twice the width. Find the length and width of the rectangle.
- Answer
-
25 ft, 50 ft
The length of the rectangle is three times the width. The perimeter of a rectangle is 72 feet. Find the length and width of the rectangle.
The length of the rectangle is three meters less than twice the width. The perimeter of a rectangle is 36 meters. Find the dimensions of the rectangle.
- Answer
-
7 m, 11 m
The length of a rectangle is five inches more than twice the width. The perimeter is 34 inches. Find the length and width.
The perimeter of a triangle is 39 feet. One side of the triangle is one foot longer than the second side. The third side is two feet longer than the second side. Find the length of each side.
- Answer
-
12 ft, 13 ft, 14 ft
The perimeter of a triangle is 35 feet. One side of the triangle is five feet longer than the second side. The third side is three feet longer than the second side. Find the length of each side.
One side of a triangle is twice the smallest side. The third side is five feet more than the shortest side. The perimeter is 17 feet. Find the lengths of all three sides.
- Answer
-
3 ft, 6 ft, 8 ft
One side of a triangle is three times the smallest side. The third side is three feet more than the shortest side. The perimeter is 13 feet. Find the lengths of all three sides.
The perimeter of a rectangular field is 560 yards. The length is 40 yards more than the width. Find the length and width of the field.
- Answer
-
120 yd, 160 yd
The perimeter of a rectangular atrium is 160 feet. The length is 16 feet more than the width. Find the length and width of the atrium.
A rectangular parking lot has perimeter 250 feet. The length is five feet more than twice the width. Find the length and width of the parking lot.
- Answer
-
40 ft, 85 ft
A rectangular rug has perimeter 240 inches. The length is 12 inches more than twice the width. Find the length and width of the rug.
In the following exercises, solve. Approximate answers to the nearest tenth, if necessary.
A 13-foot string of lights will be attached to the top of a 12-foot pole for a holiday display as shown. How far from the base of the pole should the end of the string of lights be anchored?
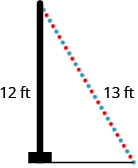
- Answer
-
5 feet
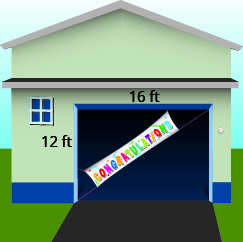
Pam wants to put a banner across her garage door diagonally, as shown, to congratulate her son for his college graduation. The garage door is 12 feet high and 16 feet wide. How long should the banner be to fit the garage door?
Chi is planning to put a diagonal path of paving stones through her flower garden as shown. The flower garden is a square with side 10 feet. What will the length of the path be?

- Answer
-
14.1 feet
Brian borrowed a 20-foot extension ladder to use when he paints his house. If he sets the base of the ladder six feet from the house as shown, how far up will the top of the ladder reach?

Everyday Math
Converting temperature While on a tour in Greece, Tatyana saw that the temperature was 40° Celsius. Solve for F in the formula \(C=\frac{5}{9}(F−32)\) to find the Fahrenheit temperature.
- Answer
-
\(104° \text{F}\)
Converting temperature Yon was visiting the United States and he saw that the temperature in Seattle one day was 50° Fahrenheit. Solve for C in the formula \(F=\frac{9}{5}C+32\) to find the Celsius temperature
Christa wants to put a fence around her triangular flowerbed. The sides of the flowerbed are six feet, eight feet and 10 feet. How many feet of fencing will she need to enclose her flowerbed?
- Answer
-
24 ft
Jose just removed the children’s play set from his back yard to make room for a rectangular garden. He wants to put a fence around the garden to keep the dog out. He has a 50-foot roll of fence in his garage that he plans to use. To fit in the backyard, the width of the garden must be 10 feet. How long can he make the other side?
Writing Exercises
If you need to put tile on your kitchen floor, do you need to know the perimeter or the area of the kitchen? Explain your reasoning.
- Answer
-
Answers will vary.
If you need to put a fence around your backyard, do you need to know the perimeter or the area of the backyard? Explain your reasoning.
Look at the two figures below.
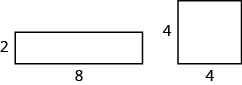
ⓐ Which figure looks like it has the larger area? Which looks like it has the larger perimeter?
ⓑ Now calculate the area and perimeter of each figure. Which has the larger area? Which has the larger perimeter?ⓒ Were the results of part (b) the same as your answers in part (a)? Is that surprising to you?
- Answer
-
ⓐ Answers will vary. ⓑ The areas are the same. The \(2×8\) rectangle has a larger perimeter than the \(4×4\) square.
ⓒ Answers will vary.
Write a geometry word problem that relates to your life experience, then solve it and explain all your steps.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?


