2.7E: Exercises

Last updated
Save as PDF

Page ID: 32412

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Solve Compound Inequalities with “and”

In the following exercises, solve each inequality, graph the solution, and write the solution in interval notation.

$x<3$ and $x\geq 1$

$x\leq 4$ and $x>−2$

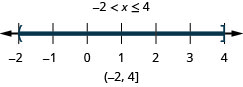
Answer: $The solution is negative 2 is less than x which is less than or equal to 4. Its graph has an open circle at 1negative 2 and a closed circle at 4 with shading between the open and closed circles. Its interval notation is negative 2 to 4 within a parenthesis and a bracket.$

$x\geq −4$ and $x\leq −1$

$x>−6$ and $x<−3$

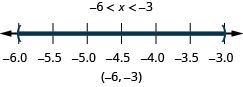
Answer: $The solution is negative 6 is less than x which is less than negative 3. Its graph has an open circle at negative 6 and an open circle at negative 3 with shading between open circles. Its interval notation is negative 6 to negative 3 within parentheses.$

$5x−2<8$ and $6x+9\geq 3$

$4x−1<7$ and $2x+8\geq 4$

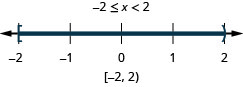
Answer: $The solution is negative 2 is less than or equal to x which is less than 2. Its graph has a closed circle at negative 2 and an open circle at 2 with shading between the closed and open circles. Its interval notation is negative 2 to 2 within a bracket and a parenthesis.$

$4x+6\leq 2$ and
$2x+1\geq −5$

$4x−2\leq 4$ and
$7x−1>−8$

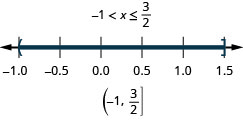
Answer: $The solution is negative 1 is less than x which is less than or equal to three-halves. Its graph has an open circle at negative 1 and a closed circle at three-halves with shading between the open and closed circles. Its interval notation is negative 1 to three-halves within a parenthesis and a bracket.$

$2x−11<5$ and
$3x−8>−5$

$7x−8<6$ and
$5x+7>−3$

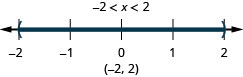
Answer: $The solution is negative 2 is less than x which is less than 2. Its graph has an open circle at negative 2 and an open circle at 2 with shading between the open circles. Its interval notation is negative 2 to 2 within parentheses.$

$4(2x−1)\leq 12$ and
$2(x+1)<4$

$5(3x−2)\leq 5$ and
$3(x+3)<3$

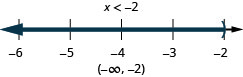
Answer: $The solution is x is less than negative 2. Its graph has an open circle at negative 2 and is shaded to the left. Its interval notation is negative infinity to negative 2 within parentheses.$

$3(2x−3)>3$ and
$4(x+5)\geq 4$

$−3(x+4)<0$ and
$−1(3x−1)\leq 7$

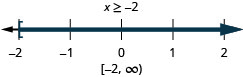
Answer: $The solution is x is greater than or equal to negative 2. Its graph has a closed circle at negative 2 and is shaded to the right. Its interval notation is negative 2 to infinity within a bracket and a parenthesis.$

$\frac{1}{2}(3x−4)\leq 1$ and
$\frac{1}{3}(x+6)\leq 4$

$\frac{3}{4}(x−8)\leq 3$ and
$\frac{1}{5}(x−5)\leq 3$

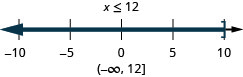
Answer: $The solution is x is less than or equal to 12. Its graph has a closed circle at 12 and is shaded to the left. Its interval notation is negative infinity to 12 within a parenthesis and a bracket.$

$5x−2\leq 3x+4$ and
$3x−4\geq 2x+1$

$\frac{3}{4}x−5\geq −2$ and
$−3(x+1)\geq 6$

Answer

$\frac{2}{3}x−6\geq −4$ and
$−4(x+2)\geq 0$

$\frac{1}{2}(x−6)+2<−5$ and
$4−\frac{2}{3}x<6$

Answer: $The solution is a contradiction. So, there is no solution. As a result, there is no graph or the number line or interval notation.$

$−5\leq 4x−1<7$

$−3<2x−5\leq 1$

Answer: $The solution is 1 is less than x which is less than or equal to 3. Its graph has an open circle at 1 and a closed circle at 3 and is shaded between the open and closed circles. Its interval notation is 1 to 3 within a parenthesis and a bracket.$

$5<4x+1<9$

$−1<3x+2<8$

Answer

$−8<5x+2\leq −3$

$−6\leq 4x−2<−2$

Answer: $The solution is negative 1 is less than or equal to x which is less than or 0. Its graph has a closed circle at negative 1 and an open circle at 0 and is shaded between the closed and open circles. Its interval notation is negative 1 to 0 within a bracket and a parenthesis.$

Solve Compound Inequalities with “or”

In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.

$x\leq −2$ or $x>3$

$x\leq −4$ or $x>−3$

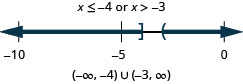
Answer: $The solution is x is less than or equal to negative 4 or x is greater than negative 3. The graph of the solutions on a number line has a closed circle at negative 4 and shading to the left and an open circle at negative 3 with shading to the right. The interval notation is the union of negative infinity to negative 4 within a parenthesis and a bracket and negative 3 and infinity within parentheses.$

$x<2$ or $x\geq 5$

$x<0$ or $x\geq 4$

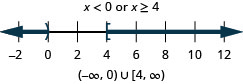
Answer: $The solution is x is less than 0 or x is greater than or equal to 2. The graph of the solutions on a number line has an open circle at 0 and shading to the left and a closed circle at 4 with shading to the right. The interval notation is the union of negative infinity to 0 within parentheses and 4 to infinity within a bracket and parenthesis.$

$2+3x\leq 4$ or
$5−2x\leq −1$

$4−3x\leq −2$ or
$2x−1\leq −5$

Answer

$2(3x−1)<4$ or
$3x−5>1$

$3(2x−3)<−5$ or
$4x−1>3$

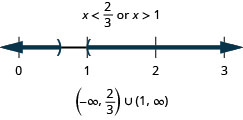
Answer: $The solution is x is less than two-thirds or x is greater than 1. The graph of the solutions on a number line has an open circle at two-thirds and shading to the left and an open circle at 1 with shading to the right. The interval notation is the union of negative infinity to two-thirds within parentheses and 1 and infinity within parentheses.$

$\frac{3}{4}x−2>4$ or $4(2−x)>0$

$\frac{2}{3}x−3>5$ or $3(5−x)>6$

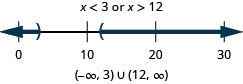
Answer: $The solution is x is less than 3 or x is greater than 12. The graph of the solutions on a number line has an open circle at 3 and shading to the left and an open circle at 12 with shading to the right. The interval notation is the union of negative infinity to 3 within parentheses and 12 and infinity within parentheses.$

$3x−2>4$ or $5x−3\leq 7$

$2(x+3)\geq 0$ or
$3(x+4)\leq 6$

Answer: $The solution is an identity. Its solution on the number line is shaded for all values. The solution in interval notation is negative infinity to infinity within parentheses.$

$\frac{1}{2}x−3\leq 4$ or
$\frac{1}{3}(x−6)\geq −2$

$\frac{3}{4}x+2\leq −1$ or
$\frac{1}{2}(x+8)\geq −3$

Answer: $The solution is an identity. Its solution on the number line is shaded for all values. The solution in interval notation is negative infinity to infinity within parentheses.$

Mixed practice

In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.

$3x+7\leq 1$ and
$2x+3\geq −5$

$6(2x−1)>6$ and
$5(x+2)\geq 0$

Answer

$4−7x\geq −3$ or
$5(x−3)+8>3$

$\frac{1}{2}x−5\leq 3$ or
$\frac{1}{4}(x−8)\geq −3$

Answer: $The solution is an identity. Its solution on the number line is shaded for all values. The solution in interval notation is negative infinity to infinity within parentheses.$

$−5\leq 2x−1<7$

$\frac{1}{5}(x−5)+6<4$ and
$3−\frac{2}{3}x<5$

Answer: $The inequality is a contradiction. So, there is no solution. As a result, there is no graph on the number line or interval notation.$

$4x−2>6$ or
$3x−1\leq −2$

$6x−3\leq 1$ and
$5x−1>−6$

Answer: $The solution is negative 1 is less than x which is less than or equal to two-thirds. Its graph has an open circle at negative 1 and a closed circle at two-thirds and is shaded between the open and closed circles. Its interval notation is negative 1 to two-thirds within a parenthesis and a bracket.$

$−2(3x−4)\leq 2$ and
$−4(x−1)<2$

$−5\leq 3x−2\leq 4$

Answer: $The solution is negative 1 is less than or equal to x which is less than 2. Its graph has a closed circle at negative 1 and a closed circle at 2 and is shaded between the closed circles. Its interval notation is negative 1 to 4 within brackets.$

Solve Applications with Compound Inequalities

In the following exercises, solve.

Penelope is playing a number game with her sister June. Penelope is thinking of a number and wants June to guess it. Five more than three times her number is between 2 and 32. Write a compound inequality that shows the range of numbers that Penelope might be thinking of.

Gregory is thinking of a number and he wants his sister Lauren to guess the number. His first clue is that six less than twice his number is between four and forty-two. Write a compound inequality that shows the range of numbers that Gregory might be thinking of.

Answer: $5\leq n\leq 24$

Andrew is creating a rectangular dog run in his back yard. The length of the dog run is 18 feet. The perimeter of the dog run must be at least 42 feet and no more than 72 feet. Use a compound inequality to find the range of values for the width of the dog run.

Elouise is creating a rectangular garden in her back yard. The length of the garden is 12 feet. The perimeter of the garden must be at least 36 feet and no more than 48 feet. Use a compound inequality to find the range of values for the width of the garden.

Answer: $6\leq w\leq 12$

Everyday Math

Blood Pressure A person’s blood pressure is measured with two numbers. The systolic blood pressure measures the pressure of the blood on the arteries as the heart beats. The diastolic blood pressure measures the pressure while the heart is resting.

ⓐ Let x be your systolic blood pressure. Research and then write the compound inequality that shows you what a normal systolic blood pressure should be for someone your age.

ⓑ Let y be your diastolic blood pressure. Research and then write the compound inequality that shows you what a normal diastolic blood pressure should be for someone your age.

Body Mass Index (BMI) is a measure of body fat is determined using your height and weight.

ⓐ Let x be your BMI. Research and then write the compound inequality to show the BMI range for you to be considered normal weight.

ⓑ Research a BMI calculator and determine your BMI. Is it a solution to the inequality in part (a)?

Answer: ⓐ answers vary ⓑ answers vary

Writing Exercises

In your own words, explain the difference between the properties of equality and the properties of inequality.

Explain the steps for solving the compound inequality $2−7x\geq −5$ or $4(x−3)+7>3$.

Answer: Answers will vary.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$This table has four columns and four rows. The first row is a header and it labels each column, “I can…”, “Confidently,” “With some help,” and “No-I don’t get it!” In row 2, the I can was solve compound inequalities with “and.” In row 3, the I can was solve compound inequalities with “or.” In row 4, the I can was solve applications with compound inequalities.$

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

Search

Text Color

Text Size

Margin Size

Font Type

Practice Makes Perfect

Everyday Math

Writing Exercises

Self Check