2.8E: Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Practice Makes Perfect
Solve Absolute Value Equations
In the following exercises, solve.
ⓐ |x|=6 ⓑ |y|=−3
ⓒ |z|=0
ⓐ |x|=4 ⓑ |y|=−5
ⓒ |z|=0
- Answer
-
ⓐ x=4,x=−4 ⓑ no solution ⓒ z=0
ⓐ |x|=7ⓑ\(|y|=−11
ⓒ |z|=0
ⓐ |x|=3 ⓑ |y|=−1
ⓒ |z|=0
- Answer
-
ⓐ x=3,x=−3 ⓑ no solution ⓒ z=0
|2x−3|−4=1
|4x−1|−3=0
- Answer
-
x=1,x=−12
|3x−4|+5=7
|4x+7|+2=5
- Answer
-
x=−1,x=−52
4|x−1|+2=10
3|x−4|+2=11
- Answer
-
x=7,x=1
3|4x−5|−4=11
3|x+2|−5=4
- Answer
-
x=1,x=−5
−2|x−3|+8=−4
−3|x−4|+4=−5
- Answer
-
x=7,x=1
|34x−3|+7=2
|35x−2|+5=2
- Answer
-
no solution
|12x+5|+4=1
|14x+3|+3=1
- Answer
-
no solution
|3x−2|=|2x−3|
|4x+3|=|2x+1|
- Answer
-
x=−1,x=−23
|6x−5|=|2x+3|
|6−x|=|3−2x|
- Answer
-
x=−3,x=3
Solve Absolute Value Inequalities with “less than”
In the following exercises, solve each inequality. Graph the solution and write the solution in interval notation.
|x|<5
|x|<1
- Answer
-

|x|≤8
|x|≤3
- Answer
-
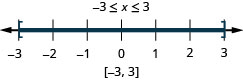
|3x−3|≤6
|2x−5|≤3
- Answer
-

|2x+3|+5<4
|3x−7|+3<1
- Answer
-
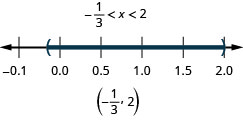
|4x−3|<1
|6x−5|<7
- Answer
-
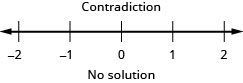
|x−4|≤−1
|5x+1|≤−2
- Answer
-
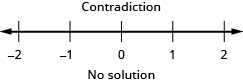
Solve Absolute Value Inequalities with “greater than”
In the following exercises, solve each inequality. Graph the solution and write the solution in interval notation.
|x|>3
|x|>6
- Answer
-
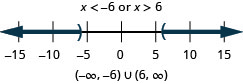
|x|≥2
|x|≥5
- Answer
-
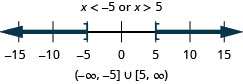
|3x−8|>−1
|x−5|>−2
- Answer
-
|3x−2|>4
|2x−1|>5
- Answer
-
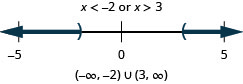
|x+3|≥5
|x−7|≥1
- Answer
-
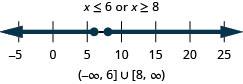
3|x|+4≥1
5|x|+6≥1
- Answer
-
In the following exercises, solve. For each inequality, also graph the solution and write the solution in interval notation.
2|x+6|+4=8
|3x−4|≥2
- Answer
-
x=4,x=27
|6x−5|=|2x+3|
|4x−3|<5
- Answer
-
x=3,x=2
|2x−5|+2=3
|3x+1|−3=7
- Answer
-
x=3,x=−113
|7x+2|+8<4
5|2x−1|−3=7
- Answer
-
x=32,x=−12
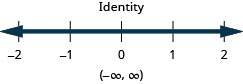
|x−7|>−3
|8−x|=|4−3x|
- Answer
-
Solve Applications with Absolute Value
In the following exercises, solve.
A chicken farm ideally produces 200,000 eggs per day. But this total can vary by as much as 25,000 eggs. What is the maximum and minimum expected production at the farm?
An organic juice bottler ideally produces 215,000 bottle per day. But this total can vary by as much as 7,500 bottles. What is the maximum and minimum expected production at the bottling company?
- Answer
-
The minimum to maximum expected production is 207,500 to 2,225,000 bottles
In order to insure compliance with the law, Miguel routinely overshoots the weight of his tortillas by 0.5 gram. He just received a report that told him that he could be losing as much as $100,000 per year using this practice. He now plans to buy new equipment that guarantees the thickness of the tortilla within 0.005 inches. If the ideal thickness of the tortilla is 0.04 inches, what thickness of tortillas will be guaranteed?
At Lilly’s Bakery, the ideal weight of a loaf of bread is 24 ounces. By law, the actual weight can vary from the ideal by 1.5 ounces. What range of weight will be acceptable to the inspector without causing the bakery being fined?
- Answer
-
The acceptable weight is 22.5 to 25.5 ounces.
Writing Exercises
Write a graphical description of the absolute value of a number
In your own words, explain how to solve the absolute value inequality, |3x−2|≥4.
- Answer
-
Answers will vary.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
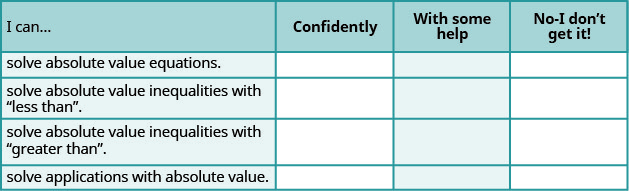
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?


