3.1E: Exercises
- Page ID
- 31079
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Verbal
Exercise \(\PageIndex{1}\)
Explain how to add complex numbers.
- Answer
-
Add the real parts together and the imaginary parts together.
Exercise \(\PageIndex{2}\)
What is the basic principle in multiplication of complex numbers?
Exercise \(\PageIndex{3}\)
Give an example to show the product of two imaginary numbers is not always imaginary.
- Answer
-
\(i\) times \(i\) equals –1, which is not imaginary. (answers will vary)
Exercise \(\PageIndex{4}\)
What is a characteristic of the plot of a real number in the complex plane?
Algebraic
For the following exercises, evaluate the algebraic expressions.
Exercise \(\PageIndex{5}\)
If \(f(x)=x^2+x−4\), evaluate \(f(2i)\).
- Answer
-
\(−8+2i\)
Exercise \(\PageIndex{6}\)
If \(f(x)=x^3−2\), evaluate \(f(i)\).
Exercise \(\PageIndex{7}\)
If \(f(x)=x^2+3x+5\),evaluate \(f(2+i)\).
- Answer
-
\(14+7i\)
Exercise \(\PageIndex{8}\)
If \(f(x)=2x^2+x−3\), evaluate \(f(2−3i)\).
Exercise \(\PageIndex{9}\)
If \(f(x)=\frac{x+1}{2−x}\), evaluate \(f(5i)\).
- Answer
-
\(−\frac{23}{29}+\frac{15}{29}i\)
Exercise \(\PageIndex{10}\)
If \(f(x)=\frac{1+2x}{x+3}\), evaluate \(f(4i)\).
Graphical
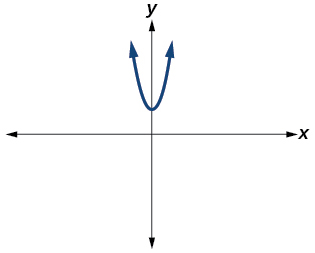
For the following exercises, determine the number of real and nonreal solutions for each quadratic function shown.
Exercise \(\PageIndex{11}\)

- Answer
-
2 real and 0 nonreal
Exercise \(\PageIndex{12}\)
For the following exercises, plot the complex numbers on the complex plane.
Exercise \(\PageIndex{13}\)
\(1−2i\)
- Answer
-
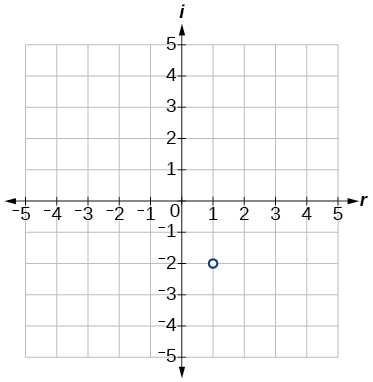
Exercise \(\PageIndex{14}\)
\(−2+3i\)
Exercise \(\PageIndex{15}\)
\(i\)
- Answer
-
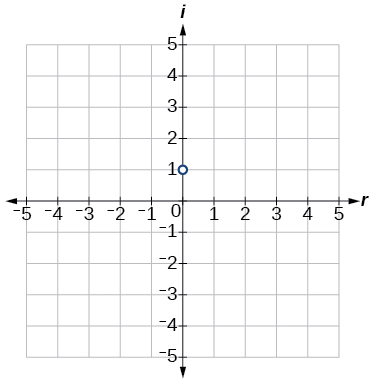
Exercise \(\PageIndex{16}\)
\(−3−4i\)
Numeric
For the following exercises, perform the indicated operation and express the result as a simplified complex number.
Exercise \(\PageIndex{17}\)
\((3+2i)+(5−3i)\)
- Answer
-
\(8−i\)
Exercise \(\PageIndex{18}\)
\((−2−4i)+(1+6i)\)
Exercise \(\PageIndex{19}\)
\((−5+3i)−(6−i)\)
- Answer
-
\(−11+4i\)
Exercise \(\PageIndex{20}\)
\((2−3i)−(3+2i)\)
Exercise \(\PageIndex{21}\)
\((−4+4i)−(−6+9i)\)
- Answer
-
\(2−5i\)
Exercise \(\PageIndex{22}\)
\((2+3i)(4i)\)
Exercise \(\PageIndex{23}\)
\((5−2i)(3i)\)
- Answer
-
\(6+15i\)
Exercise \(\PageIndex{24}\)
\((6−2i)(5)\)
Exercise \(\PageIndex{25}\)
\((−2+4i)(8)\)
- Answer
-
\(−16+32i\)
Exercise \(\PageIndex{26}\)
\((2+3i)(4−i)\)
Exercise \(\PageIndex{27}\)
\((−1+2i)(−2+3i)\)
- Answer
-
\(−4−7i\)
Exercise \(\PageIndex{28}\)
\((4−2i)(4+2i)\)
Exercise \(\PageIndex{29}\)
\((3+4i)(3−4i)\)
- Answer
-
25
Exercise \(\PageIndex{30}\)
\(\frac{3+4i}{2}\)
Exercise \(\PageIndex{31}\)
\(\frac{6−2i}{3}\)
- Answer
-
\(2−\frac{2}{3}i\)
Exercise \(\PageIndex{32}\)
\(\frac{−5+3i}{2i}\)
Exercise \(\PageIndex{33}\)
\(\frac{6+4i}{i}\)
- Answer
-
\(4−6i\)
Exercise \(\PageIndex{34}\)
\(\frac{2−3i}{4+3i}\)
Exercise \(\PageIndex{35}\)
\(\frac{3+4i}{2−i}\)
- Answer
-
\(\frac{2}{5}+\frac{11}{5}i\)
Exercise \(\PageIndex{36}\)
\(\frac{2+3i}{2−3i}\)
Exercise \(\PageIndex{37}\)
\(\sqrt{−9}+3\sqrt{−16}\)
- Answer
-
\(15i\)
Exercise \(\PageIndex{38}\)
\(−\sqrt{−4}−4\sqrt{−25}\)
Exercise \(\PageIndex{39}\)
\(\frac{2+\sqrt{−12}}{2}\)
- Answer
-
\(1+i\sqrt{3}\)
Exercise \(\PageIndex{40}\)
\(\frac{4+\sqrt{−20}}{2}\)
Exercise \(\PageIndex{41}\)
\(i^8\)
- Answer
-
\(1\)
Exercise \(\PageIndex{42}\)
\(i^{15}\)
Exercise \(\PageIndex{43}\)
\(i^{22}\)
- Answer
-
\(−1\)
Technology
For the following exercises, use a calculator to help answer the questions.
44. Evaluate \((1+i)^k\) for \(k=4, 8, \) and \(12\).Predict the value if \(k=16\).
45. Evaluate \((1−i)^k\) for \(k=2, 6,\) and \(10\).Predict the value if \(k=14\).
Answer: 128i
46. Evaluate (1+i)k−(1−i)k for \(k=4\), 8, and 12. Predict the value for \(k=16\).
47. Show that a solution of \(x^6+1=0\) is \(\frac{\sqrt{3}}{2}+\frac{1}{2}i\).
Answer: \((\frac{\sqrt{3}}{2}+\frac{1}{2}i)^6=−1\)
48. Show that a solution of \(x^8−1=0\) is \(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\).
Extensions
For the following exercises, evaluate the expressions, writing the result as a simplified complex number.
49. \(\frac{1}{i}+\frac{4}{i^3}\)
Answer: \(3i\)
50. \(\frac{1}{i^{11}}−\frac{1}{i^{21}}\)
51. \(i^7(1+i^2)\)
Answer: 0
52. \(i^{−3}+5i^7\)
53. \(\frac{(2+i)(4−2i)}{(1+i)}\)
Answer: \(5 – 5i\)
54. \(\frac{(1+3i)(2−4i)}{(1+2i)}\)
55. \(\frac{(3+i)^2}{(1+2i)^2}\)
Answer: \(−2i\)
56. \(\frac{3+2i}{2+i}+(4+3i)\)
57. \(\frac{4+i}{i}+\frac{3−4i}{1−i}\)
Answer: \(\frac{9}{2}−\frac{9}{2}i\)
58. \(\frac{3+2i}{1+2i}−\frac{2−3i}{3+i}\)

