3.6E: Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Section Exercises
Verbal
1. Describe a use for the Remainder Theorem.
Answer: The theorem can be used to evaluate a polynomial.
2. Explain why the Rational Zero Theorem does not guarantee finding zeros of a polynomial function.
3. What is the difference between rational and real zeros?
Answer: Rational zeros can be expressed as fractions whereas real zeros include irrational numbers.
4. If Descartes’ Rule of Signs reveals a no change of signs or one sign of changes, what specific conclusion can be drawn?
5. If synthetic division reveals a zero, why should we try that value again as a possible solution?
Answer: Polynomial functions can have repeated zeros, so the fact that number is a zero doesn’t preclude it being a zero again.
Algebraic
For the following exercises, use the Remainder Theorem to find the remainder.
6. (x4−9x2+14)÷(x−2)
7. (3x3−2x2+x−4)÷(x+3)
Answer: −106
8. (x4+5x3−4x−17)÷(x+1)
9. (−3x2+6x+24)÷(x−4)
Answer: 0
10. (5x5−4x4+3x3−2x2+x−1)÷(x+6)
11. (x4−1)÷(x−4)
Answer: 255
12. (3x3+4x2−8x+2)÷(x−3)
13. (4x3+5x2−2x+7)÷(x+2)
Answer: −1
For the following exercises, use the Factor Theorem to find all real zeros for the given polynomial function and one factor.
14. f(x)=2x3−9x2+13x−6;x−1
15. f(x)=2x3+x2−5x+2;x+2
Answer: −2,1,12
16. f(x)=3x3+x2−20x+12;x+3
17. f(x)=2x3+3x2+x+6;x+2
Answer: −2
18. f(x)=−5x3+16x2−9;x−3
19. x3+3x2+4x+12;x+3
Answer: −3
20. 4x3−7x+3;x−1
21. 2x3+5x2−12x−30,2x+5
Answer: −52,√6,−√6
For the following exercises, use the Rational Zero Theorem to find all real zeros.
22. x3−3x2−10x+24=0
23.2x3+7x2−10x−24=0
Answer: 2,−4,−32
24. x3+2x2−9x−18=0
25. x3+5x2−16x−80=0
Answer: 4,−4,−5
26. x3−3x2−25x+75=0
27. 2x3−3x2−32x−15=0
Answer: 5,−3,−12
28. 2x3+x2−7x−6=0
29. 2x3−3x2−x+1=0
Answer: 12,1+√52,1−√52
30. 3x3−x2−11x−6=0
31. 2x3−5x2+9x−9=0
Answer: 32
32. 2x3−3x2+4x+3=0
33. x4−2x3−7x2+8x+12=0
Answer: 2,3,−1,−2
34. x4+2x3−9x2−2x+8=0
35. 4x4+4x3−25x2−x+6=0
Answer: 12,−12,2,−3
36. 2x4−3x3−15x2+32x−12=0
37. x4+2x3−4x2−10x−5=0
Answer: −1,−1,√5,−√5
38. 4x3−3x+1=0
39. 8x4+26x3+39x2+26x+6
Answer: −34,−12
For the following exercises, find all complex solutions (real and non-real).
40. x3+x2+x+1=0
41. x3−8x2+25x−26=0
Answer: 2,3+2i,3−2i
42. x3+13x2+57x+85=0
43. 3x3−4x2+11x+10=0
Answer: −23,1+2i,1−2i
44. x4+2x3+22x2+50x−75=0
45. 2x3−3x2+32x+17=0
Answer: −12,1+4i,1−4i
Graphical
For the following exercises, use Descartes’ Rule to determine the possible number of positive and negative solutions. Confirm with the given graph.
46. f(x)=x3−1
47. f(x)=x4−x2−1
Answer: 1 positive, 1 negative
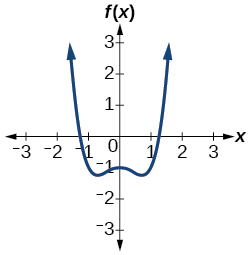
48. f(x)=x3−2x2−5x+6
49. f(x)=x3−2x2+x−1
Answer: 3 or 1 positive, 0 negative
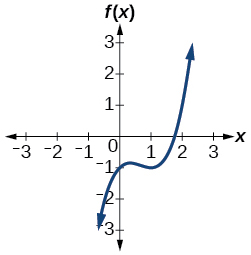
50. f(x)=x4+2x3−12x2+14x−5
51. f(x)=2x3+37x2+200x+300
Answer: 0 positive, 3 or 1 negative
.jpg?revision=1&size=bestfit&width=343&height=256)
52. f(x)=x3−2x2−16x+32
53. f(x)=2x4−5x3−5x2+5x+3
Answer: 2 or 0 positive, 2 or 0 negative
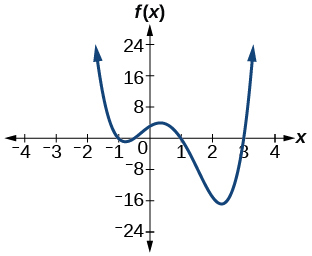
54. f(x)=2x4−5x3−14x2+20x+8
55. f(x)=10x4−21x2+11
Answer: 2 or 0 positive, 2 or 0 negative
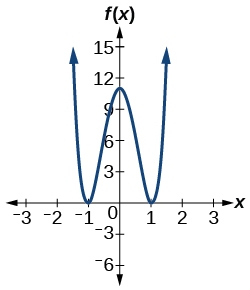
Numeric
For the following exercises, list all possible rational zeros for the functions.
f(x)=x4+3x3−4x+4
f(x)=2x3+3x2−8x+5
±5,±1,±52
f(x)=3x3+5x2−5x+4
f(x)=6x4−10x2+13x+1
±1,±12,±13,±16
f(x)=4x5−10x4+8x3+x2−8
Technology
For the following exercises, use your calculator to graph the polynomial function. Based on the graph, find the rational zeros. All real solutions are rational.
f(x)=6x3−7x2+1
1,12,−13
f(x)=4x3−4x2−13x−5
f(x)=8x3−6x2−23x+6
2,14,−32
f(x)=12x4+55x3+12x2−117x+54
f(x)=16x4−24x3+x2−15x+25
54
Extensions
For the following exercises, construct a polynomial function of least degree possible using the given information.
Real roots: –1, 1, 3 and (2,f(2))=(2,4)
Real roots: –1 (with multiplicity 2 and 1) and (2,f(2))=(2,4)
f(x)=49(x3+x2−x−1)
Real roots: –2,12
(with multiplicity 2) and (−3,f(−3))=(−3,5)
Real roots:−12,0,12 and (−2,f(−2))=(−2,6)
f(x)=−15(4x3−x)
Real roots: –4, –1, 1, 4 and (−2,f(−2))=(−2,10)
Real-World Applications
For the following exercises, find the dimensions of the box described.
The length is twice as long as the width. The height is 2 inches greater than the width. The volume is 192 cubic inches.
8 by 4 by 6 inches
The length, width, and height are consecutive whole numbers. The volume is 120 cubic inches.
The length is one inch more than the width, which is one inch more than the height. The volume is 86.625 cubic inches.
5.5 by 4.5 by 3.5 inches
The length is three times the height and the height is one inch less than the width. The volume is 108 cubic inches.
The length is 3 inches more than the width. The width is 2 inches more than the height. The volume is 120 cubic inches.
8 by 5 by 3 inches
For the following exercises, find the dimensions of the right circular cylinder described.
The radius is 3 inches more than the height. The volume is 16π cubic meters.
The height is one less than one half the radius. The volume is 72π cubic meters.
Radius = 6 meters, Height = 2 meters
The radius and height differ by one meter. The radius is larger and the volume is 48π cubic meters.
The radius and height differ by two meters. The height is greater and the volume is 28.125π cubic meters.
Radius = 2.5 meters, Height = 4.5 meters
80. The radius is \frac{1}{3} meter greater than the height. The volume is \frac{98}{9}π cubic meters.

