4.2E: Exercises

Last updated
Save as PDF

Page ID: 31099

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Verbal

1) What role does the horizontal asymptote of an exponential function play in telling us about the end behavior of the graph?

Answer:: An asymptote is a line that the graph of a function approaches, as $x$ either increases or decreases without bound. The horizontal asymptote of an exponential function tells us the limit of the function’s values as the independent variable gets either extremely large or extremely small.

2) What is the advantage of knowing how to recognize transformations of the graph of a parent function algebraically?

Algebraic

3) The graph of $f(x) = 3^x$is reflected about the $y$-axis and stretched vertically by a factor of $4$What is the equation of the new function, $g(x)$?State its $y$-intercept, domain, and range.

Answer:

4) The graph of $f(x)=\left ( \frac{1}{2} \right )^{-x}$is reflected about the $y$-axis and compressed vertically by a factor of $\left ( \frac{1}{5} \right )$What is the equation of the new function, $g(x)$State its $y$-intercept, domain, and range.

5) The graph of $f(x)=10^x$ is reflected about the $x$-axis and shifted upward $7$ units. What is the equation of the new function, $g(x)$?State its $y$-intercept, domain, and range.

Answer:

6) The graph of $f(x)=(1.68)^x$ is shifted right $3$ units, stretched vertically by a factor of

Exercise $\PageIndex{7}$

The graph of $f(x)=2\left ( \frac{1}{4} \right )^{x-2}$ is shifted left $2$ units, stretched vertically by a factor of $4$, reflected across the $x$-axis, and then shifted downward $4$ units. What is the equation of the new function, $g(x)$? State its $y$-intercept, domain, and range.

Answer: $g(x)=-8\left ( \frac{1}{4} \right )^x - 4$; $y$-intercept: $(0,-12)$; Domain: all real numbers; Range: all real numbers less than $0$.

Graphical

For the following exercises, graph the function and its reflection across the $y$-axis on the same axes, and give the $y$-intercept.

8) $f(x)=3\left ( \frac{1}{2} \right )^x$

Exercise $\PageIndex{9}$

$g(x)=-2(0.25)^x$

Answer

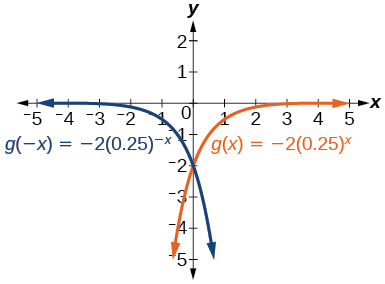
$CNX_PreCalc_Figure_04_02_202.jpg$

$y$-intercept: $(0,-2)$

10) $h(x)=6(1.75)^{-x}$

For the following exercises, graph each set of functions on the same axes.

11) $f(x)=3\left ( \frac{1}{4} \right )^x, g(x)=3(2)^x, h(x)=3(4)^x$

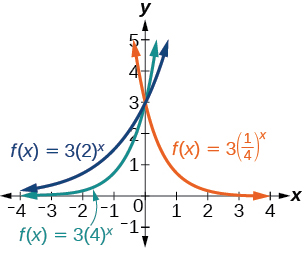
Answer:: $CNX_PreCalc_Figure_04_02_204.jpg$

12) $f(x)=\frac{1}{4}(3)^x, g(x)=2(3)^x, h(x)=4(3)^x$

For the following exercises, match each function with one of the graphs in Figure below.

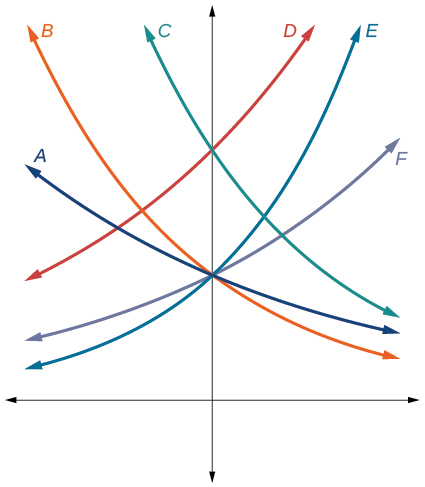
$CNX_PreCalc_Figure_04_02_206.jpg$

13) $f(x)=2(0.69)^x$

Answer:: B

14) $f(x)=2(1.28)^x$

15) $f(x)=2(0.81)^x$

Answer:: A

16) $f(x)=4(1.28)^x$

17) $f(x)=2(1.59)^x$

Answer:: E

18) $f(x)=4(0.69)^x$

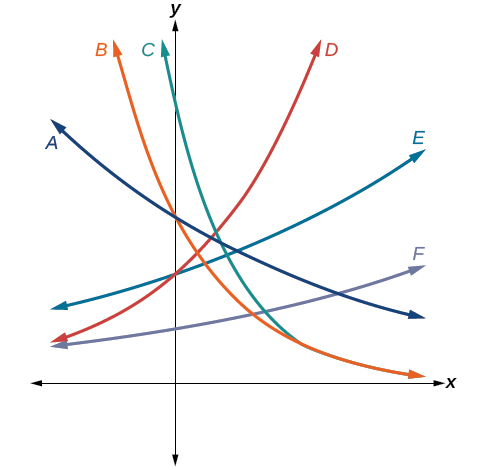
For the following exercises, use the graphs shown in Figure below. All have the form $f(x)=ab^x$.

$CNX_PreCalc_Figure_04_02_207.jpg$

Exercise $\PageIndex{19}$

Which graph has the largest value for $b$ ?

Answer: D

Exercise $\PageIndex{20}$

Which graph has the smallest value for $b$?

Exercise $\PageIndex{21}$

Which graph has the largest value for $a$?

Answer: C

Exercise $\PageIndex{22}$

Which graph has the smallest value for $a$?

For the following exercises, graph the function and its reflection about the $x$-axis on the same axes.

23) $f(x)=\frac{1}{2}(4)^x$

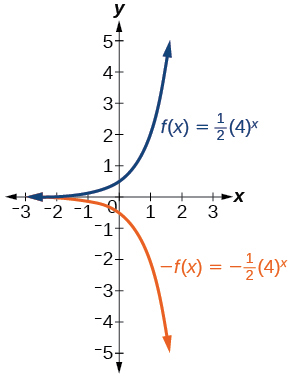
Answer:: $CNX_PreCalc_Figure_04_02_208.jpg$

24) $f(x)=3(0.75)^x-1$

25) $f(x)=-4(2)^x+2$

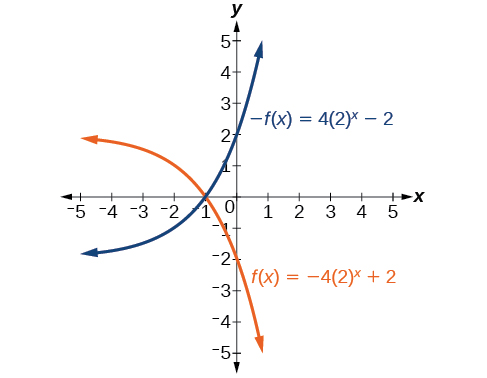
Answer:: $CNX_PreCalc_Figure_04_02_210.jpg$

For the following exercises, graph the transformation of $f(x)=2^x$ Give the horizontal asymptote, the domain, and the range.

26) $f(x)=2^{-x}$

Exercise $\PageIndex{27}$

$h(x)=2^x+3$

Answer

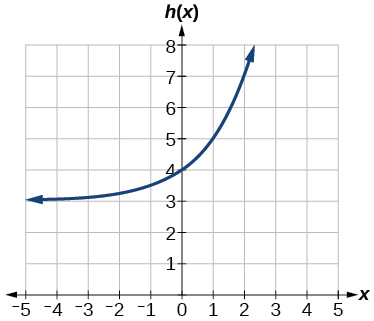
$CNX_PreCalc_Figure_04_02_212.jpg$

Horizontal asymptote: $y=3$ Domain: all real numbers; Range: all real numbers strictly greater than $3$.

28) $f(x)=2^{x-2}$

For the following exercises, describe the end behavior of the graphs of the functions.

29) $f(x)=-5(4)^x-1$

Answer:

As $x\rightarrow \infty , f(x)\rightarrow -\infty$

As $x\rightarrow -\infty , f(x)\rightarrow -1$

30) $f(x)=3\left ( \frac{1}{2} \right )^x-2$

31) $f(x)=3(4)^{-x}+2$

Answer:

As $x\rightarrow \infty , f(x)\rightarrow 2$

As $x\rightarrow -\infty , f(x)\rightarrow \infty$

For the following exercises, start with the graph of $f(x)=4^x$ Then write a function that results from the given transformation.

32) Shift $f(x)$ $4$ units upward

33) Shift $f(x)$ $3$ units downward

Answer:: $f(x)=4^x-3$

34) Shift $f(x)$ $2$ units left

35) Shift $f(x)$ $5$ units right

Answer:: $f(x)=4^{x-5}$

36) Reflect $f(x)$ about the $x$-axis

37) Reflect $f(x)$ about the $y$-axis

Answer:: $f(x)=4^{-x}$

For the following exercises, each graph is a transformation of $f(x)=2^x$ Write an equation describing the transformation.

38)

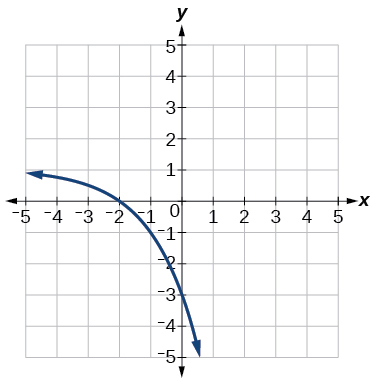
$CNX_PreCalc_Figure_04_02_214.jpg$

Exercise $\PageIndex{39}$

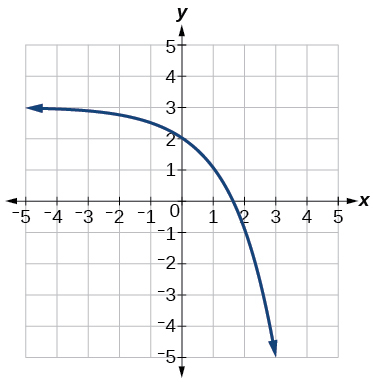
$CNX_PreCalc_Figure_04_02_215.jpg$

Answer: $y=-2^x+3$

40)

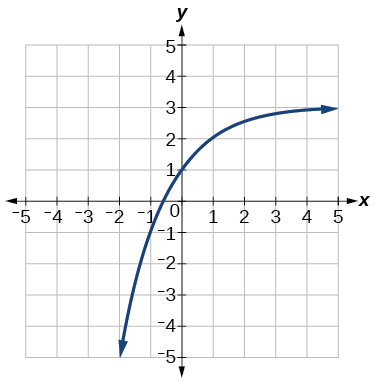
$CNX_PreCalc_Figure_04_02_216.jpg$

For the following exercises, find an exponential equation for the graph.

Exercise $\PageIndex{41}$

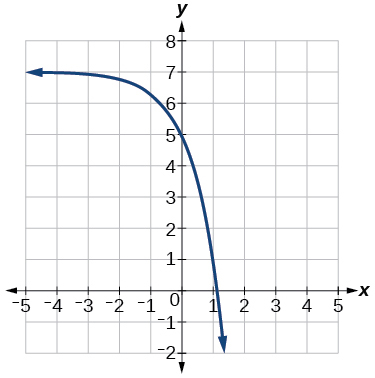
$CNX_PreCalc_Figure_04_02_217.jpg$

Answer: $y=-2(3)^x+7$

42)

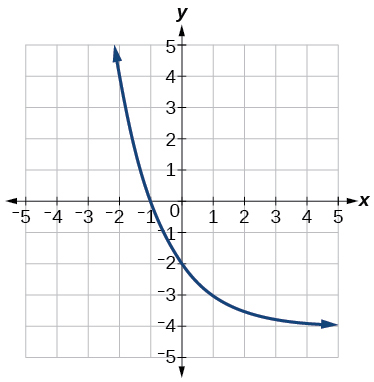
$CNX_PreCalc_Figure_04_02_218.jpg$

Numeric

For the following exercises, evaluate the exponential functions for the indicated value of $x$.

Exercise $\PageIndex{43}$

$g(x)=\frac{1}{3}(7)^{x-2}$, for $x=6$.

Answer: $g(6)=800+\frac{1}{3}\approx 800.3333$

44) $f(x)=4(2)^{x-1}-2$ for $f(5)$.

45) $h(x)=-\frac{1}{2}\left ( \frac{1}{2} \right )^x+6$ for $h(-7)$.

Answer:: $h(-7)=-58$

Technology

For the following exercises, use a graphing calculator to approximate the solutions of the equation. Round to the nearest thousandth.

46) $-50=\left ( \frac{1}{2} \right )^{-x}$

47) $116=\left ( \frac{1}{4} \right )\left ( \frac{1}{8} \right )^x$

Answer:: $x\approx -2.953$

48) $12=2(3)^x+1$

49) $5=3\left ( \frac{1}{2} \right )^{x-1}-2$

Answer:: $x\approx -0.222$

50) $-30=-4(2)^{x+2}+2$

Extensions

51) Explore and discuss the graphs of

Answer:: The graph of $G(x)=\left ( \frac{1}{b} \right )^x$ is the refelction about the $y$-axis of the graph of $F(x)=(b)^x$; For any real number $b>0$ and function $f(x)=(b)^x$ the graph of $\left ( \frac{1}{b} \right )^x$ is the the reflection about the $y$-axis, $F(-x)$.

52) Prove the conjecture made in the previous exercise.

53) Explore and discuss the graphs of $f(x) = 4^x$, $g(x)=4^{x-2}$, and $h(x)=\left ( \frac{1}{16} \right )4^x$ Then make a conjecture about the relationship between the graphs of the functions $b^x$ and $\left ( \frac{1}{b^n} \right )b^x$ for any real number $n$ and real number $b>0$.

Answer:: The graphs of $g(x)$ and $h(x)$ are the same and are a horizontal shift to the right of the graph of $f(x)$; For any real number $n$, real number $b>0$, and function $f(x)=b^x$ the graph of $\left ( \frac{1}{b^n} \right )b^x$ is the horizontal shift $f(x-n)$.

54) Prove the conjecture made in the previous exercise.