4.4: Graphs of Logarithmic Functions

Skills to Develop

• Identify the domain of a logarithmic function.
• Graph logarithmic functions.

In Graphs of Exponential Functions, we saw how creating a graphical representation of an exponential model gives us another layer of insight for predicting future events. How do logarithmic graphs give us insight into situations? Because every logarithmic function is the inverse function of an exponential function, we can think of every output on a logarithmic graph as the input for the corresponding inverse exponential equation. In other words, logarithms give the cause for an effect.

To illustrate, suppose we invest \($2500\) in an account that offers an annual interest rate of \(5%\),compounded continuously. We already know that the balance in our account for any year \(t\) can be found with the equation \(A=2500e^{0.05t}\).

But what if we wanted to know the year for any balance? We would need to create a corresponding new function by interchanging the input and the output; thus we would need to create a logarithmic model for this situation. By graphing the model, we can see the output (year) for any input (account balance). For instance, what if we wanted to know how many years it would take for our initial investment to double? Figure \(\PageIndex{1}\) shows this point on the logarithmic graph.

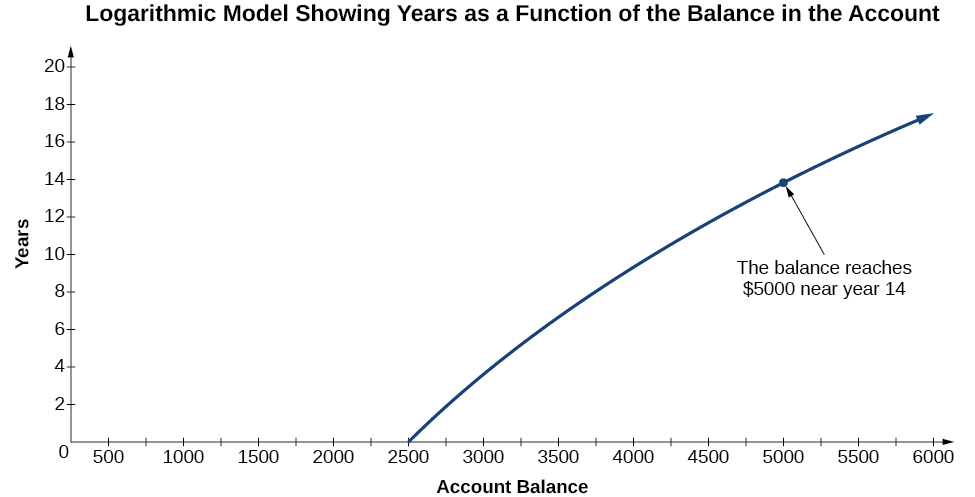
Figure \(\PageIndex{1}\)

In this section we will discuss the values for which a logarithmic function is defined, and then turn our attention to graphing the family of logarithmic functions.

Finding the Domain of a Logarithmic Function

Before working with graphs, we will take a look at the domain (the set of input values) for which the logarithmic function is defined.

Recall that the exponential function is defined as \(y=b^x\) for any real number \(x\) and constant \(b>0\), \(b≠1\), where

• The domain of \(y\) is \((−\infty,\infty)\).
• The range of \(y\) is \((0,\infty)\).

In the last section we learned that the logarithmic function \(y={\log}_b(x)\) is the inverse of the exponential function \(y=b^x\). So, as inverse functions:

• The domain of \(y={\log}_b(x)\) is the range of \(y=b^x\): \((0,\infty)\).
• The range of \(y={\log}_b(x)\) is the domain of \(y=b^x\): \((−\infty,\infty)\).

Transformations of the toolkit function \(y={\log}_b(x)\) behave similarly to those of other functions. Just as with other toolkit functions, we can apply the four types of transformations—shifts, stretches, compressions, and reflections—to the toolkit function without loss of shape.

In Graphs of Exponential Functions we saw that certain transformations can change the range of \(y=b^x\). Similarly, applying transformations to the toolkit function \(y={\log}_b(x)\) can change the domain. When finding the domain of a logarithmic function, therefore, it is important to remember that the domain consists only of positive real numbers. That is, the input value, or argument, of the logarithmic function must be greater than zero.

For example, consider \(f(x)={\log}_4(2x−3)\). This function is defined for any values of \(x\) such that the argument, in this case \(2x−3\),is greater than zero. To find the domain, we set up an inequality and solve for \(x\):

\[\begin{align*} 2x-3&> 0 \qquad \text {Show the argument greater than zero}\\ 2x&> 3 \qquad \text{Add 3} \\ x&> 1.5 \qquad \text{Divide by 2} \\ \end{align*}\]

In interval notation, the domain of \(f(x)={\log}_4(2x−3)\) is \((1.5,\infty)\).

Given a logarithmic function, identify the domain

1. Set up an inequality showing the argument greater than zero.
2. Solve for \(x\).
3. Write the domain in interval notation.

Example \(\PageIndex{1}\): Identifying the Domain of a Logarithmic Shift

What is the domain of \(f(x)={\log}_2(x+3)\)?

Solution

The logarithmic function is defined only when the input is positive, so this function is defined when \(x+3>0\). Solving this inequality,

\[\begin{align*} x+3&> 0 \qquad \text{The input must be positive}\\ x&> -3 \qquad \text{Subtract 3} \end{align*}\]

The domain of \(f(x)={\log}_2(x+3)\) is \((−3,\infty)\).

\(\PageIndex{1}\)

What is the domain of \(f(x)={\log}_5(x−2)+1\)?

Answer

\((2,\infty)\)

Graphing Logarithmic Functions

Now that we have a feel for the set of values for which a logarithmic function is defined, we move on to graphing logarithmic functions. The family of logarithmic functions includes the toolkit function \(y={\log}_b(x)\) along with all its transformations: shifts, stretches, compressions, and reflections.

We begin with the toolkit function \(y={\log}_b(x)\). Because every logarithmic function of this form is the inverse of an exponential function with the form \(y=b^x\), their graphs will be reflections of each other across the line \(y=x\). To illustrate this, we can observe the relationship between the input and output values of \(y=2^x\) and its equivalent \(x={\log}_2(y)\) in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\)

\(x\)	\(−3\)	\(−2\)	\(−1\)	\(0\)	\(1\)	\(2\)	\(3\)
\(2^x=y\)	\(\dfrac{1}{8}\)	\(\dfrac{1}{4}\)	\(\dfrac{1}{2}\)	\(1\)	\(2\)	\(4\)	\(8\)
\({\log}_2(y)=x\)	\(−3\)	\(−2\)	\(−1\)	\(0\)	\(1\)	\(2\)	\(3\)

Using the inputs and outputs from Table \(\PageIndex{1}\), we can build another table to observe the relationship between points on the graphs of the inverse functions \(f(x)=2^x\) and \(g(x)={\log}_2(x)\). See Table \(\PageIndex{2}\).

Table \(\PageIndex{2}\)

\(f(x)=2^x\)	\(\left(−3,\dfrac{1}{8}\right)\)	\(\left(−2,\dfrac{1}{4}\right)\)	\(\left(−1,\dfrac{1}{2}\right)\)	\((0,1)\)	\((1,2)\)	\((2,4)\)	\((3,8)\)
\(g(x)={\log}_2(x)\)	\(\left(\dfrac{1}{8},−3\right)\)	\(\left(\dfrac{1}{4},−2\right)\)	\(\left(\dfrac{1}{2},−1\right)\)	\((1,0)\)	\((2,1)\)	\((4,2)\)	\((8,3)\)

As expected, the \(x\)- and \(y\)-coordinates are reversed for the inverse functions. Figure \(\PageIndex{2}\) shows the graph of \(f\) and \(g\).

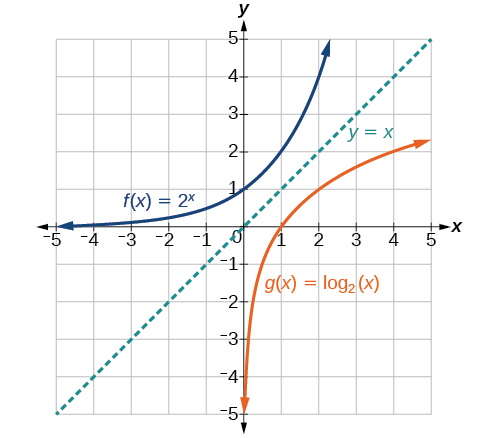
Figure \(\PageIndex{2}\): Notice that the graphs of \(f(x)=2^x\) and \(g(x)={\log}_2(x)\) are reflections about the line \(y=x\).

Observe the following from the graph:

• \(f(x)=2^x\) has a \(y\)-intercept at \((0,1)\) and \(g(x)={\log}_2(x)\) has an \(x\)-intercept at \((1,0)\).
• The domain of \(f(x)=2^x\), \((−\infty,\infty)\), is the same as the range of \(g(x)={\log}_2(x)\).
• The range of \(f(x)=2^x\), \((0,\infty)\), is the same as the domain of \(g(x)={\log}_2(x)\).

CHARACTERISTICS OF THE GRAPH OF THE toolkit FUNCTION, \(f(x) = \log_b(x)\)

For any real number \(x\) and constant \(b>0\), \(b≠1\), we can see the following characteristics in the graph of \(f(x)={\log}_b(x)\):

• one-to-one function
• vertical asymptote: \(x=0\)
• domain: \((0,\infty)\)
• range: \((−\infty,\infty)\) 
• \(x\)-intercept: \((1,0)\) and key point \((b,1)\)
• \(y\)-intercept: none
• increasing if \(b>1\)
• decreasing if \(0<b<1\)

See Figure \(\PageIndex{3}\).

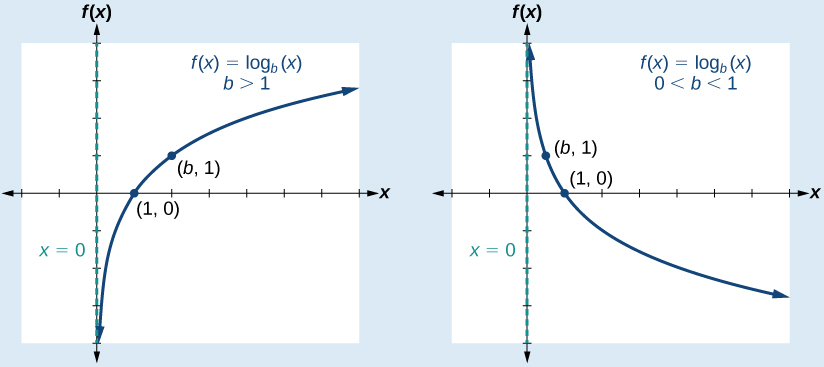
Figure \(\PageIndex{3}\)

Figure \(\PageIndex{4}\) shows how changing the base \(b\) in \(f(x)={\log}_b(x)\) can affect the graphs. Observe that the graphs compress vertically as the value of the base increases. (Note: recall that the function \(\ln(x)\) has base \(e≈2.718\).)

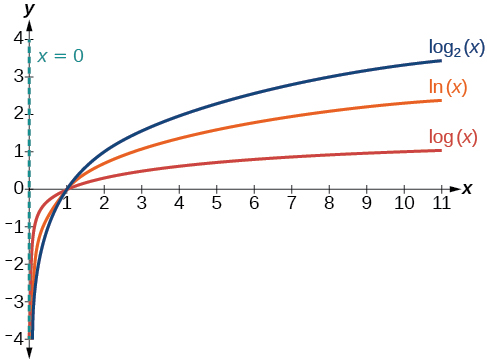
Figure \(\PageIndex{4}\): The graphs of three logarithmic functions with different bases, all greater than 1.

Given a logarithmic function with the form \(f(x)={\log}_b(x)\), graph the function.

1. Draw and label the vertical asymptote, \(x=0\).
2. Plot the x-intercept, \((1,0)\).
3. Plot the key point \((b,1)\).
4. Draw a smooth curve through the points.
5. State the domain, \((0,\infty)\),the range, \((−\infty,\infty)\), and the vertical asymptote, \(x=0\).

Example \(\PageIndex{2}\): Graphing a Logarithmic Function with the Form \(f(x) = log_b(x)\)

Graph \(f(x)={\log}_5(x)\). State the domain, range, and asymptote.

Solution

Before graphing, identify the behavior and key points for the graph.

• Since \(b=5\) is greater than one, we know the function is increasing. The left tail of the graph will approach the vertical asymptote \(x=0\), and the right tail will increase slowly without bound.
• The \(x\)-intercept is \((1,0)\).
• The key point \((5,1)\) is on the graph.
• We draw and label the asymptote, plot and label the points, and draw a smooth curve through the points (see Figure \(\PageIndex{5}\)).

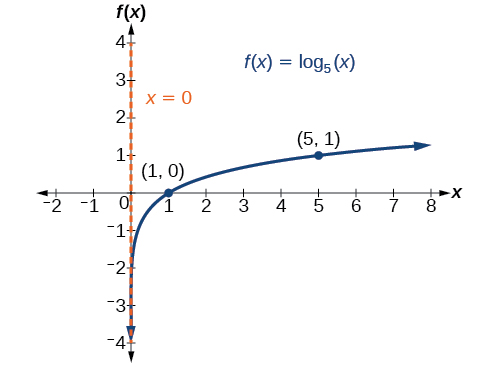
Figure \(\PageIndex{5}\)

The domain is \((0,\infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).

\(\PageIndex{2}\)

Graph \(f(x)={\log}_{\tfrac{1}{5}}(x)\). State the domain, range, and asymptote.

Answer

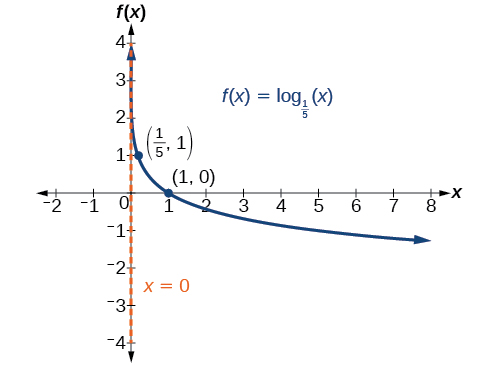
Figure \(\PageIndex{6}\)

The domain is \((0,\infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).

Graphing Transformations of Logarithmic Functions

As we mentioned in the beginning of the section, transformations of logarithmic graphs behave similarly to those of other toolkit functions. We can shift, stretch, compress, and reflect the toolkit function \(y={\log}_b(x)\) without loss of shape.

Graphing a Horizontal Shift of \(f(x) = log_b(x)\)

When a positive constant \(c\) is added or subtracted to the input of the toolkit function \(f(x)={\log}_b(x)\), the result is a horizontal shift \(c\) units left if \(c\) is positive and \(c\) units right if \(c\) is negative. To visualize horizontal shifts, we can observe the general graph of the toolkit function \(f(x)={\log}_b(x)\) and for \(c>0\) alongside the shift left, \(g(x)={\log}_b(x+c)\), and the shift right, \(h(x)={\log}_b(x−c)\). See Figure \(\PageIndex{7}\).

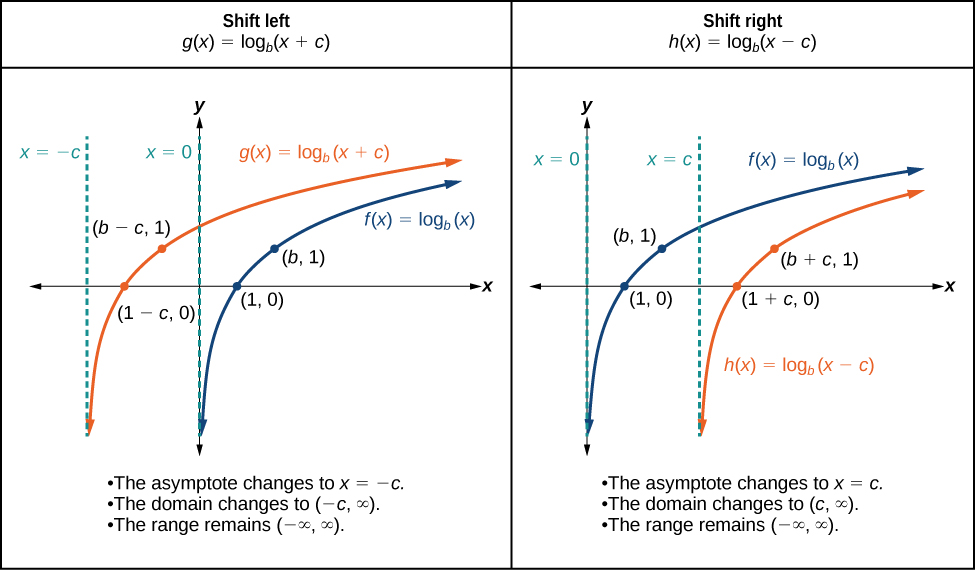
Figure \(\PageIndex{7}\)

HORIZONTAL SHIFTS OF THE toolkit FUNCTION \(y=\log_b(x)\)

For any constant \(c\), the function \(f(x)={\log}_b(x+c)\)

• shifts the toolkit function \(y={\log}_b(x)\) left \(c\) units if \(c>0\).
• shifts the toolkit function \(y={\log}_b(x)\) right \(|c|\) units if \(c<0\).
• has the vertical asymptote \(x=−c\).
• has domain \((−c,\infty)\).
• has range \((−\infty,\infty)\).

Given a logarithmic function with the form \(f(x)=\log_b(x+c)\), graph the translation.

1. Identify the horizontal shift:
   • If \(c>0\),shift the graph of \(f(x)={\log}_b(x)\) left \(c\) units.
   • If \(c<0\),shift the graph of \(f(x)={\log}_b(x)\) right \(|c|\) units.
2. Draw the vertical asymptote \(x=−c\).
3. Identify three key points from the toolkit function. Find new coordinates for the shifted functions by subtracting \(c\) from the \(x\) coordinate.
4. Label the three points.
5. The domain is \((−c,\infty)\),the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=−c\).

Example \(\PageIndex{3}\): Graphing a Horizontal Shift of the toolkit Function \(y = \log_b(x)\)

Sketch the horizontal shift \(f(x)={\log}_3(x−2)\) alongside its toolkit function. Include the key points and asymptotes on the graph. State the domain, range, and asymptote.

Solution

Since the function is \(f(x)={\log}_3(x−2)\), we notice \(x+(−2)=x–2\).

Thus \(c=−2\), so \(c<0\). This means we will shift the function \(f(x)={\log}_3(x)\) right 2 units.

The vertical asymptote is \(x=−(−2)\) or \(x=2\).

Consider the three key points from the toolkit function, \(\left(\dfrac{1}{3},−1\right)\), \((1,0)\),and \((3,1)\).

The new coordinates are found by adding \(2\) to the \(x\) coordinates.

Label the points \(\left(\dfrac{7}{3},−1\right)\), \((3,0)\),and \((5,1)\).

The domain is \((2,\infty)\),the range is \((−\infty,\infty)\),and the vertical asymptote is \(x=2\).

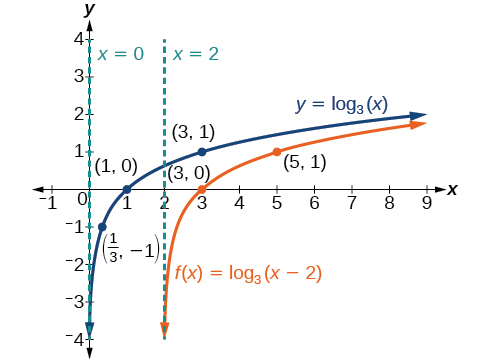
Figure \(\PageIndex{8}\)

\(\PageIndex{3}\)

Sketch a graph of \(f(x)={\log}_3(x+4)\) alongside its toolkit function. Include the key points and asymptotes on the graph. State the domain, range, and asymptote.

Answer

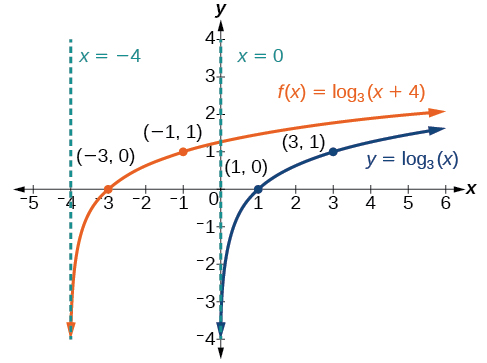
Figure \(\PageIndex{9}\)

The domain is \((−4,\infty)\),the range \((−\infty,\infty)\),and the asymptote \(x=–4\).

Graphing a Vertical Shift of \(y = \log_b(x)\)

When a positive constant \(d\) is added or subtracted to the toolkit function \(f(x)={\log}_b(x)\),the result is a vertical shift \(d\) units up if \(d\) is added and \(d\) units down if \(d\) is subtracted. 

VERTICAL SHIFTS OF THE toolkit FUNCTION \(y=\log_b(x)\)

For any constant \(d\), the function \(f(x)=\log_b(x)+d\)

• shifts the toolkit function \(y={\log}_b(x)\) up \(d\) units if \(d>0\).
• shifts the toolkit function \(y={\log}_b(x)\) down \(|d|\) units if \(d<0\).
• has the vertical asymptote \(x=0\).
• has domain \((0,\infty)\).
• has range \((−\infty,\infty)\).

Given a logarithmic function with the form \(f(x)={\log}_b(x)+d\), graph the translation.

1. Identify the vertical shift:
   • If \(d>0\), shift the graph of \(f(x)={\log}_b(x)\) up \(d\) units.
   • If \(d<0\), shift the graph of \(f(x)={\log}_b(x)\) down \(|d|\) units.
2. Draw the vertical asymptote \(x=0\).
3. Identify three key points from the toolkit function. Find new coordinates for the shifted functions by adding \(d\) to the \(y\)-coordinate.
4. Label the three points.
5. The domain is \((0,\infty)\), the range is \((−\infty,\infty)\),and the vertical asymptote is \(x=0\).

Example \(\PageIndex{4}\): Graphing a Vertical Shift of the toolkit Function \(y = log_b(x)\)

Sketch a graph of \(f(x)={\log}_3(x)−2\) alongside its toolkit function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

Solution

Since the function is \(f(x)={\log}_3(x)−2\),we notice \(d= -2\). Thus \(d<0\).

This means we will shift the function \(f(x)={\log}_3(x)\) down \(2\) units.

The vertical asymptote is \(x=0\).

Consider these three key points from the toolkit function, \(\left(\dfrac{1}{3},−1\right)\), \((1,0)\),and \((3,1)\).

The new coordinates are found by subtracting \(2\) from the \(y\)-coordinates.

Label the points \(\left(\dfrac{1}{3},−3\right)\), \((1,−2)\), and \((3,−1)\).

The domain is \((0,\infty)\),the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).

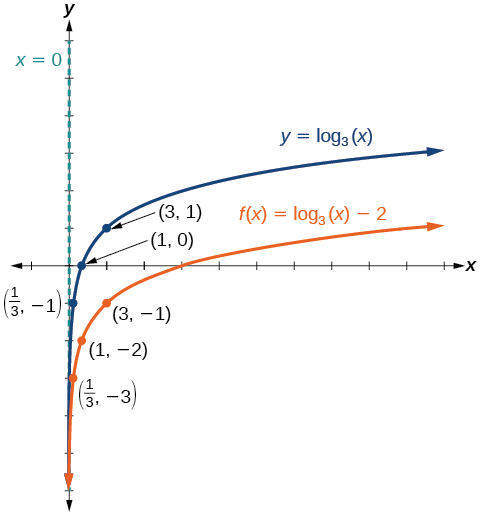
Figure \(\PageIndex{10}\)

The domain is \((0,\infty)\),the range is \((−\infty,\infty)\),and the vertical asymptote is \(x=0\).

\(\PageIndex{4}\)

Sketch a graph of \(f(x)={\log}_2(x)+2\) alongside its toolkit function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

Answer

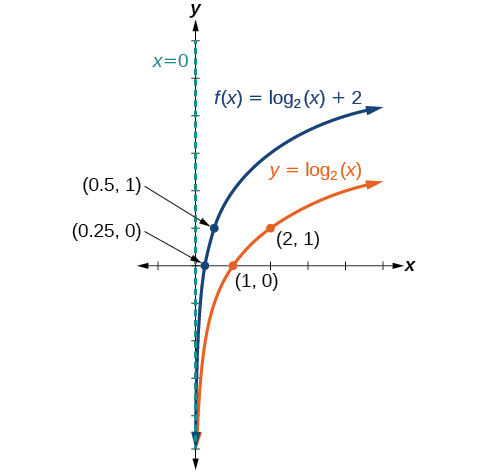
Figure \(\PageIndex{11}\)

The domain is \((0,\infty)\),the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).
Good job, trying this problem, and checking your answer! If you look carefully at the graph of the shifted function \(f\), you will see that the labeled points are not vertical shifts of the two labeled points on the toolkit function. What are the correct points of the vertical shifts? Show them to your professor and make her give you extra credit!

Graphing Stretches and Compressions of \(y = \log_b(x)\)

When the toolkit function \(f(x)={\log}_b(x)\) is multiplied by a constant \(a>0\), the result is a vertical stretch or compression of the original graph.

VERTICAL STRETCHES AND COMPRESSIONS OF THE toolkit FUNCTION \(y=\log_b(x)\)

For any constant \(a>0\), the function \(f(x)=a\log_b(x)\)

• stretches the toolkit function \(y={\log}_b(x)\) vertically by a factor of \(a\) if \(a>1\).
• compresses the toolkit function \(y={\log}_b(x)\) vertically by a factor of \(a\) if \(0<a<1\).
• has the vertical asymptote \(x=0\).
• has the \(x\)-intercept \((1,0)\).
• has domain \((0,\infty)\).
• has range \((−\infty,\infty)\).

Given a logarithmic function with the form \(f(x)=a\log_b(x)\), \(a>0\), graph the translation.

1. Identify the vertical stretch or compressions:
   • If \(a>1\), the graph of \(f(x)={\log}_b(x)\) is stretched by a factor of \(a\) units.
   • If \(0<a<1\), the graph of \(f(x)={\log}_b(x)\) is compressed by a factor of \(a\) units.
2. Draw the vertical asymptote \(x=0\).
3. Identify three key points from the toolkit function. Find new coordinates for the shifted functions by multiplying the \(y\)-coordinates by \(a\).
4. Label the three points.
5. The domain is \((0,\infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).

Example \(\PageIndex{5}\): Graphing a Stretch or Compression of the toolkit Function \(y = log_b(x)\)

Sketch a graph of \(f(x)=2{\log}_4(x)\) alongside its toolkit function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

Solution

Since the function is \(f(x)=2{\log}_4(x)\),we will notice \(a=2\).

This means we will stretch the function \(f(x)={\log}_4(x)\) by a factor of \(2\).

The vertical asymptote is \(x=0\).

Consider three key points from the toolkit function, \((2,1/2)\), \((1,0)\), and \((4,1)\).

The new coordinates are found by multiplying the \(y\)-coordinates by \(2\).

Label the points \((2,1)\), \((1,0)\), and \((4,2)\). (If you are looking carefully, you will see that one of the key points from the toolkit function has not been labeled, and one of the new points on the stretched function have not been labeled. Give your professor the coordinates of the two missing points, and get extra credit!)

The domain is \((0, \infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\). See Figure \(\PageIndex{12}\).

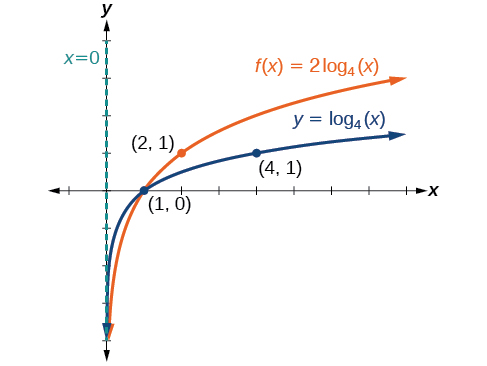
Figure \(\PageIndex{12}\)

The domain is \((0,\infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).

\(\PageIndex{5}\)

Sketch a graph of \(f(x)=\dfrac{1}{2}{\log}_4(x)\) alongside its toolkit function. Include some key points and asymptote on the graph. State the domain, range, and asymptote.

Answer

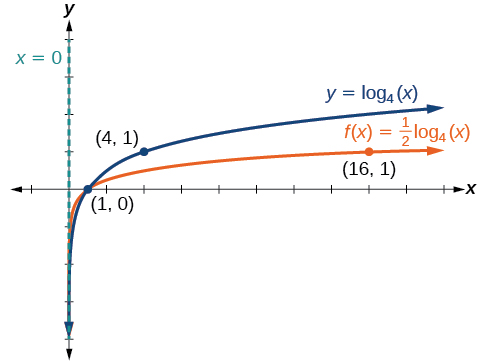
Figure \(\PageIndex{13}\)

The domain is \((0,\infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).
Again with the missing labels for key points! Can you name them?

Example \(\PageIndex{6}\): Combining a Shift and a Stretch

Sketch a graph of \(f(x)=5{\log}(x+2).\) State the domain, range, and asymptote.

Solution

Remember: what happens inside parentheses happens first. First, we move the graph left \(2\) units, then stretch the function vertically by a factor of \(5\), as in Figure \(\PageIndex{16}\). The vertical asymptote will be shifted to \(x=−2\). The \(x\)-intercept will be \((−1,0)\). The domain will be \((−2,\infty)\). Two points will help give the shape of the graph: \((−1,0)\) and \((8,5)\). We chose \(x=8\) as the x-coordinate of one point to graph because when \(x=8\), \(x+2=10\), the base of the common logarithm.

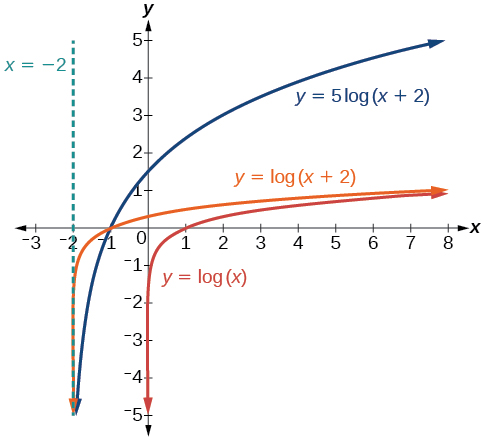
Figure \(\PageIndex{14}\)

The domain is \((−2,\infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=-2\).

\(\PageIndex{6}\)

Sketch a graph of the function \(f(x)=3{\log}(x−2)+1\). State the domain, range, and asymptote.

Answer

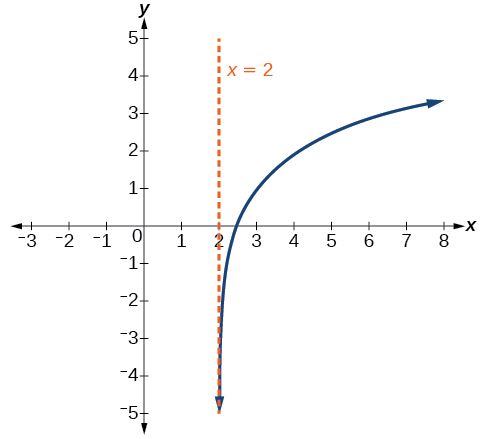
Figure \(\PageIndex{15}\)

The domain is \((2,\infty)\),the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=2\).

Graphing Reflections of \(f(x) = \log_b(x)\)

When the toolkit function \(f(x)={\log}_b(x)\) is multiplied by \(−1\),the result is a reflection across the \(x\)-axis. When the input is multiplied by \(−1\),the result is a reflection across the \(y\)-axis.

REFLECTIONS OF THE toolkit FUNCTION \(y=\log_b(x)\)

The function \(f(x)=-\log_b(x)\)

• reflects the toolkit function \(y={\log}_b(x)\) across the \(x\)-axis.
• has domain, \((0,\infty)\), range, \((−\infty,\infty)\), and vertical asymptote, \(x=0\), which are unchanged from the toolkit function.

The function \(f(x)={\log}_b(−x)\)

• reflects the toolkit function \(y={\log}_b(x)\) across the \(y\)-axis.
• has domain \((−\infty,0)\).
• has range, \((−\infty,\infty)\), and vertical asymptote, \(x=0\), which are unchanged from the toolkit function.

Given a logarithmic function with the toolkit function \(f(x)={\log}_b(x),\) graph a translation.

Table \(\PageIndex{3}\)

If \(f(x)=-\log_b(x)\)	If \(f(x)=\log_b(−x)\)
Draw the vertical asymptote, \(x=0\).	Draw the vertical asymptote, \(x=0\).
Plot the x-intercept, \((1,0)\).	Plot the x-intercept, \((-1,0)\).
Reflect the graph of the toolkit function \(f(x)={\log}_b(x)\) across the x-axis.	Reflect the graph of the toolkit function \(f(x)={\log}_b(x)\) across the y-axis.
Draw a smooth curve through the points.	Draw a smooth curve through the points.
State the domain, \((0,\infty)\), the range, \((−\infty,\infty)\), and the vertical asymptote \(x=0\).	State the domain, \((−\infty,0)\), the range, \((−\infty,\infty)\), and the vertical asymptote \(x=0\).

Example \(\PageIndex{7}\): Graphing a Reflection of a Logarithmic Function

Sketch a graph of \(f(x)=\log(−x)\) alongside its toolkit function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

Solution

Before graphing \(f(x)=\log(−x)\), identify the behavior and key points for the graph.

• Since \(b=10\) is greater than one, we know that the toolkit function is increasing. Since the input value is multiplied by \(−1\), \(f(x)\) is a reflection of the toolkit graph across the \(y\)-axis. Thus, \(f(x)=\log(−x)\) will be decreasing as \(x\) moves from negative infinity to zero, and the right tail of the graph will approach the vertical asymptote \(x=0\). 
• The \(x\)-intercept is \((−1,0)\).
• We draw and label the asymptote, plot and label the points, and draw a smooth curve through the points.

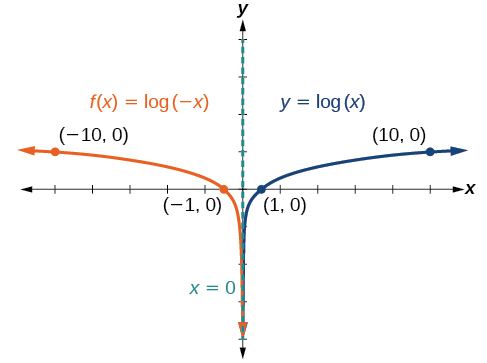
Figure \(\PageIndex{16}\)

The domain is \((−\infty,0)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).

\(\PageIndex{7}\)

Graph \(f(x)=−\log(−x)\). State the domain, range, and asymptote.

Answer

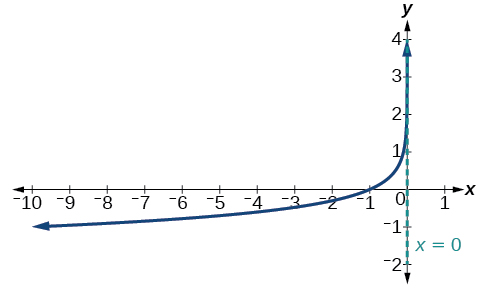
Figure \(\PageIndex{17}\)

The domain is \((−\infty,0)\),the range is \((−\infty,\infty)\),and the vertical asymptote is \(x=0\).

Given a logarithmic equation, use a graphing calculator to approximate solutions.

1. Press [Y=]. Enter the given logarithm equation or equations as Y₁= and, if needed, Y₂=.
2. Press [GRAPH] to observe the graphs of the curves and use [WINDOW] to find an appropriate view of the graphs, including their point(s) of intersection.
3. To find the value of \(x\), we compute the point of intersection. Press [2ND] then [CALC]. Select “intersect” and press [ENTER] three times. The point of intersection gives the value of \(x\),for the point(s) of intersection.

Example \(\PageIndex{8}\): Approximating the Solution of a Logarithmic Equation

Solve \(4\ln(x)+1=−2\ln(x−1)\) graphically. Round to the nearest thousandth.

Solution

Press [Y=] and enter \(4\ln(x)+1\) next to Y₁=. Then enter \(−2\ln(x−1)\) next to Y₂=. For a window, use the values \(0\) to \(5\) for \(x\0 and \(–10\) to \(10\) for \(y\). Press [GRAPH]. The graphs should intersect somewhere a little to right of \(x=1\).

For a better approximation, press [2ND] then [CALC]. Select [5: intersect] and press [ENTER] three times. The x-coordinate of the point of intersection is displayed as \(1.3385297\). (Your answer may be different if you use a different window or use a different value for Guess?) So, to the nearest thousandth, \(x≈1.339\).

\(\PageIndex{8}\)

Solve \(5\log(x+2)=4−\log(x)\) graphically. Round to the nearest thousandth.

Answer

\(x≈3.049\)

Summarizing Translations of the Logarithmic Function

Now that we have worked with each type of translation for the logarithmic function, we can summarize each in Table \(\PageIndex{4}\) to arrive at the general equation for translating exponential functions.

Table \(\PageIndex{4}\)

Translations of the toolkit Function \(y={\log}_b(x)\)
Translation	Form
Shift Horizontally \(c\) units to the left or right Vertically \(d\) units up or down	\(y={\log}_b(x+c)+d\)
Stretch and Compress Stretch if \(|a|>1\)  Compression if \(|a|<1\)	\(y=a{\log}_b(x)\)
Reflect about the \(x\)-axis	\(y=−{\log}_b(x)\)
Reflect about the \(y\)-axis	\(y={\log}_b(−x)\)
General equation for all translations	\(y=a\log_b(x+c)+d\)

TRANSLATIONS OF LOGARITHMIC FUNCTIONS

All translations of the toolkit logarithmic function, \(y={\log}_b(x)\), have the form

\(f(x)=a{\log}_b(x+c)+d\)

where the toolkit function, \(y={\log}_b(x)\), \(b>1\),is

• shifted vertically \(d\) units up or down.
• shifted horizontally to the left or right \(c\) units.
• stretched vertically by a factor of \(|a|\) if \(|a|>0\).
• compressed vertically by a factor of \(|a|\) if \(0<|a|<1\).
• reflected across the \(x\)-axis when \(a<0\).

For \(f(x)=\log(−x)\), the graph of the toolkit function is reflected across the \(y\)-axis.

Example \(\PageIndex{9}\): Finding the Vertical Asymptote of a Logarithm Graph

What is the vertical asymptote of \(f(x)=−2{\log}_3(x+4)+5\)?

Solution

The vertical asymptote is at \(x=−4\).

Analysis

The coefficient, the base, and the upward translation do not affect the asymptote. The shift of the curve \(4\) units to the left shifts the vertical asymptote to \(x=−4\).

\(\PageIndex{9}\)

What is the vertical asymptote of \(f(x)=3+\ln(x−1)\)?

Answer

\(x=1\)

Example \(\PageIndex{10}\): Finding the Equation from a Graph

Find a possible equation for the common logarithmic function graphed in Figure \(\PageIndex{18}\).

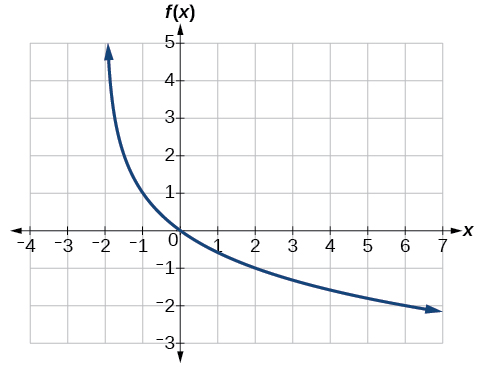
Figure \(\PageIndex{18}\)

Solution

This graph has a vertical asymptote at \(x=-2\), hence has been horizontally shifted 2 units to the left, and has been vertically reflected. We do not know yet the vertical shift or the vertical stretch. We know so far that the equation will have form:

\(f(x)=−a\log(x+2)+k\)

It appears the graph passes through the points \((-1,1)\) and \((2,–1)\). Substituting \((-1,1)\),

\[\begin{align*} 1&= -a\log(-1+2)+k \qquad \text{Substitute } (-1,1)\\ 1&= -a\log(1)+k \qquad \text{Arithmetic}\\ 1&= 0 +k \qquad\mbox{ Evaluate }\log(1)\\ 1&= k \end{align*}\]

Next, substituting in \((2,-1)\),

\[\begin{align*} -1&= -a\log(2+2)+1 \qquad \text{Substitute } (2,-1)\\ -2&= -a\log(4) \qquad \text{Arithmetic}\\ a&= \dfrac{2}{\log(4)} \qquad \text{Solve for }a \end{align*}\]

This gives us the equation \(f(x)=–\dfrac{2}{\log(4)}\log(x+2)+1\).

Analysis

We can verify this answer by comparing the function values in Table \(\PageIndex{5}\) with the points on the graph in Figure \(\PageIndex{21}\).

Table \(\PageIndex{5}\)

\(x\)	−1	0	1	2	3
\(f(x)\)	1	0	−0.58496	−1	−1.3219
\(x\)	4	5	6	7	8
\(f(x)\)	−1.5850	−1.8074	−2	−2.1699	−2.3219

\(\PageIndex{10}\)

Give the equation of the natural logarithm graphed in Figure \(\PageIndex{19}\).

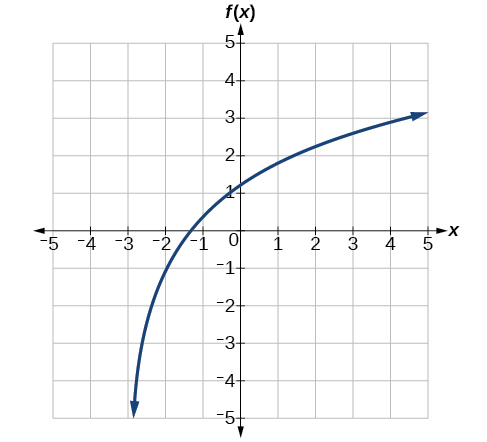
Figure \(\PageIndex{19}\)

Answer

\(f(x)=2\ln(x+3)−1\)
Partial analysis: There is a vertical asymptote at \(x=-3\), so the graph of \(y=\ln(x)\) has been shifted 3 units left. Since \(b=e \approx 2.7,\) the graph has not been reflected across the \(x\)-axis.

: Is it possible to tell the domain and range and describe the end behavior of a function just by looking at the graph?

Yes, if we know the function is a general logarithmic function. For example, look at the graph in Figure \(\PageIndex{19}\). The graph approaches \(x=−3\) (or thereabouts) more and more closely, so \(x=−3\) is, or is very close to, the vertical asymptote. It approaches from the right, so the domain is all points to the right, \({x|x>−3}\). The range, as with all general logarithmic functions, is all real numbers. And we can see the end behavior because the graph goes down as it goes left and up as it goes right. The end behavior is: as \(x\rightarrow −3^+\), \(f(x)\rightarrow −\infty\) and as \(x\rightarrow \infty\), \(f(x)\rightarrow \infty\).

Media

Access these online resources for additional instruction and practice with graphing logarithms.

• Graph an Exponential Function and Logarithmic Function
• Match Graphs with Exponential and Logarithmic Functions
• Find the Domain of Logarithmic Functions

Key Equations

General Form for the Translation of the toolkit Logarithmic Function \(f(x)={\log}_b(x)\)

\(f(x)=a{\log}_b(x+c)+d\)

Key Concepts

• To find the domain of a logarithmic function, set up an inequality showing the argument greater than zero, and solve for \(x\). See Example \(\PageIndex{1}\) and Example \(\PageIndex{2}.\)
• The graph of the toolkit function \(f(x)={\log}_b(x)\) has an x-intercept at \((1,0)\), domain \((0,\infty)\), range \((−\infty,\infty)\),vertical asymptote \(x=0\), and
  • if \(b>1\), the function is increasing.
  • if \(0<b<1\), the function is decreasing.

See Figure \(\PageIndex{3}\).

• The equation \(f(x)={\log}_b(x+c)\) shifts the toolkit function \(y={\log}_b(x)\) horizontally.
  • left \(c\) units if \(c>0\).
  • right \(c\) units if \(c<0\).

See Example \(\PageIndex{3}\).

• The equation \(f(x)={\log}_b(x)+d\) shifts the toolkit function \(y={\log}_b(x)\) vertically.
  • up \(d\) units if \(d>0\).
  • down \(d\) units if \(d<0\).

See Example \(\PageIndex{4}\).

• For any constant \(a>0\), the equation \(f(x)=a{\log}_b(x).\)
  • stretches the toolkit function \(y={\log}_b(x)\) vertically by a factor of \(a\) if \(|a|>1\).
  • compresses the toolkit function \(y={\log}_b(x)\) vertically by a factor of \(a\) if \(|a|<1.\)

See Example \(\PageIndex{5}\) and Example \(\PageIndex{6}\).

• When the toolkit function \(y={\log}_b(x)\) is multiplied by \(−1\), the result is a reflection across the x-axis. When the input is multiplied by \(−1\), the result is a reflection across the y-axis.
  • The equation \(f(x)=-{\log}_b(x)\) represents a reflection of the toolkit function across the x-axis.
  • The equation \(f(x)={\log}_b(-x)\) represents a reflection of the toolkit function across the y-axis.

See Example \(\PageIndex{7}\).

• A graphing calculator may be used to approximate solutions to some logarithmic equations. See Example \(\PageIndex{8}\).
• All translations of the logarithmic function can be summarized by the general equation \(f(x)=a{\log}_b(x+c)+d\). See Table \(\PageIndex{4}\).
• Given an equation with the general form \(f(x)=a{\log}_b(x+c)+d\),we can identify the vertical asymptote \(x=−c\) for the transformation. See Example \(\PageIndex{9}\).
• Using the general equation \(f(x)=a{\log}_b(x+c)+d\), we can write the equation of a logarithmic function given its graph. See Example \(\PageIndex{10}\).

Contributors

• Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.