1.6E: Exercises

Last updated
Save as PDF

Page ID: 31072

This page is a draft and is under active development.

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Section Exercise

Verbal

Exercise 1.6.1

How do you solve an absolute value equation?

Answer:: Isolate the absolute value term so that the equation is of the form $|A|=B$. Form one equation by setting the expression inside the absolute value symbol, $A$, equal to the expression on the other side of the equation, $B$. Form a second equation by setting $A$ equal to the opposite of the expression on the other side of the equation, $−B$. Solve each equation for the variable.

Exercise 1.6.2

How can you tell whether an absolute value function has two x-intercepts without graphing the function?

Exercise 1.6.3

When solving an absolute value function, the isolated absolute value term is equal to a negative number. What does that tell you about the graph of the absolute value function?

Answer:: The graph of the absolute value function does not cross the x-axis, so the graph is either completely above or completely below the x-axis.

Exercise 1.6.4

How can you use the graph of an absolute value function to determine the x-values for which the function values are negative?

Exercise 1.6.5

How do you solve an absolute value inequality algebraically?

Answer:: First determine the boundary points by finding the solution(s) of the equation. Use the boundary points to form possible solution intervals. Choose a test value in each interval to determine which values satisfy the inequality.

Algebraic

Exercise 1.6.6

Describe all numbers $x$ that are at a distance of 4 from the number 8. Express this using absolute value notation.

Exercise 1.6.7

Describe all numbers $x$ that are at a distance of $\dfrac{1}{2}$ from the number −4. Express this using absolute value notation.

Answer:: $|x+4|= \frac{1}{2}$

Exercise 1.6.8

Describe the situation in which the distance that point $x$ is from 10 is at least 15 units. Express this using absolute value notation.

Exercise 1.6.9

Find all function values $f(x)$ such that the distance from $f(x)$ to the value 8 is less than 0.03 units. Express this using absolute value notation.

Answer:: $|f(x)−8|<0.03$

For the following exercises, solve the equations below and express the answer using set notation.

Exercise 1.6.10

$|x+3|=9$

Exercise 1.6.11

$|6−x|=5$

Answer:: ${1,11}$

Exercise 1.6.12

$|5x−2|=11$

Exercise 1.6.13

$|4x−2|=11$

Answer:: $\{\frac{9}{4}, \frac{13}{4}\}$

Exercise 1.6.14

$2|4−x|=7$

Exercise 1.6.15

$3|5−x|=5$

Answer:: $\{\frac{10}{3},\frac{20}{3}\}$

Exercise 1.6.16

$3|x+1|−4=5$

Exercise 1.6.17

$5|x−4|−7=2$

Answer:: $\{\frac{11}{5}, \frac{29}{5}\}$

Exercise 1.6.18

$0=−|x−3|+2$

Exercise 1.6.19

$2|x−3|+1=2$

Answer:: $\{\frac{5}{2}, \frac{7}{2}\}$

Exercise 1.6.20

$|3x−2|=7$

Exercise 1.6.21

$|3x−2|=−7$

Answer:: No solution

Exercise 1.6.22

$|\frac{1}{2}x−5|=11$

Exercise 1.6.23

$| \frac{1}{3}x+5|=14$

Answer:: $\{−57,27\}$

Exercise 1.6.24

$−|\frac{1}{3}x+5|+14=0$

For the following exercises, find the x- and y-intercepts of the graphs of each function.

Exercise 1.6.25

$f(x)=2|x+1|−10$

Answer:: $(0,−8)$; $(−6,0)$, $(4,0)$

Exercise 1.6.26

$f(x)=4|x−3|+4$

Exercise 1.6.27

$f(x)=−3|x−2|−1$

Answer:: $(0,−7)$; no x-intercepts

Exercise 1.6.28

$f(x)=−2|x+1|+6$

For the following exercises, solve each inequality and write the solution in interval notation.

Exercise 1.6.29

$| x−2 |>10$

Answer:: $(−\infty,−8)\cup(12,\infty)$

Exercise 1.6.30

$2|v−7|−4\geq42$

Exercise 1.6.31

$|3x−4|\geq8$

Answer:: $−\dfrac{4}{3}{\leq}x\leq4$

Exercise 1.6.32

$|x−4|\geq8$

Exercise 1.6.33

$|3x−5|\geq-13$

Answer:: $(−\infty,− \frac{8}{3}]\cup\left[6,\infty\right)$

Exercise 1.6.34

$|3x−5|\geq−13$

Exercise 1.6.35

$|\frac{3}{4}x−5|\geq7$

Answer:: $(-\infty,-\frac{8}{3}]\cup\left[16,\infty\right)$

Exercise 1.6.36

$|\frac{3}{4}x−5|+1\leq16$

Graphical

For the following exercises, graph the absolute value function. Plot at least five points by hand for each graph.

Exercise 1.6.37

$y=|x−1|$

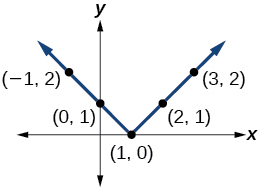
Answer:: $Graph of an absolute function with points at (-1, 2), (0, 1), (1, 0), (2, 1), and (3, 2).$

Exercise 1.6.38

$y=|x+1|$

Exercise 1.6.39

$y=|x|+1$

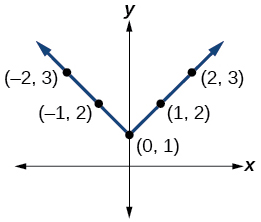
Answer:: $Graph of an absolute function with points at (-2, 3), (-1, 2), (0, 1), (1, 2), and (2, 3)$

For the following exercises, graph the given functions by hand.

Exercise 1.6.40

$y=|x|−2$

Exercise 1.6.41

$y=−|x|$

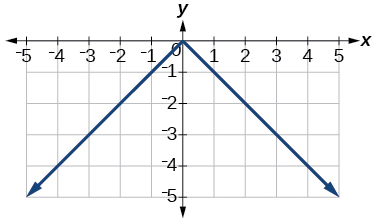
Answer:: $Graph of an absolute function.$

Exercise 1.6.42

$y=−|x|−2$

Exercise 1.6.43

$y=−|x−3|−2$

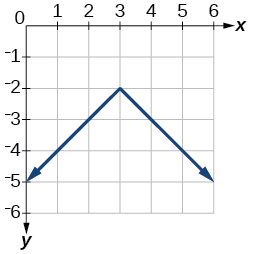
Answer:: $Graph of an absolute function.$

Exercise 1.6.44

$f(x)=−|x−1|−2$

Exercise 1.6.45

$f(x)=−|x+3|+4$

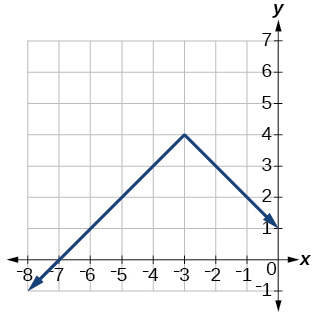
Answer:: $Graph of an absolute function.$

Exercise 1.6.46

$f(x)=2|x+3|+1$

Exercise 1.6.47

$f(x)=3|x−2|+3$

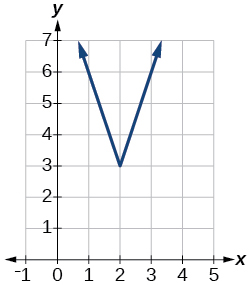
Answer:: $Graph of an absolute function.$

Exercise 1.6.48

$f(x)=|2x−4|−3$

Exercise 1.6.49

$f(x)=|3x+9|+2$

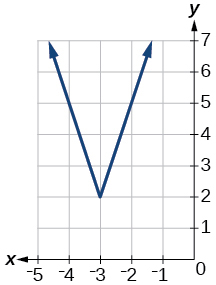
Answer:: $Graph of an absolute function.$

Exercise 1.6.50

$f(x)=−|x−1|−3$

Exercise 1.6.51

$f(x)=−|x+4|−3$

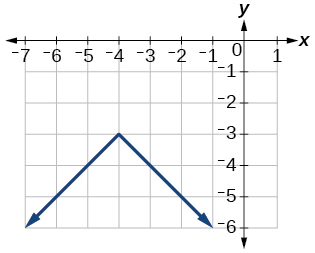
Answer:: $Graph of an absolute function.$

Exercise 1.6.52

$f(x)=\frac{1}{2}|x+4|−3$

Technology

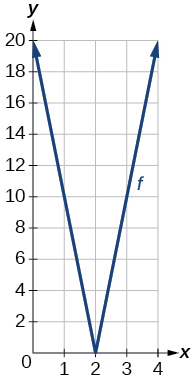
Exercise 1.6.53

Use a graphing utility to graph $f(x)=10|x−2|$ on the viewing window $[0,4]$. Identify the corresponding range. Show the graph.

Answer:

range: $[0,20]$

$Graph of an absolute value function.$

Exercise 1.6.54

Use a graphing utility to graph $f(x)=−100|x|+100$ on the viewing window $[−5,5]$. Identify the corresponding range. Show the graph.

For the following exercises, graph each function using a graphing utility. Specify the viewing window.

Exercise 1.6.55

$f(x)=−0.1|0.1(0.2−x)|+0.3$

Answer:

x-intercepts:

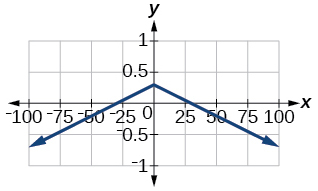
$Graph of an absolute function.$

Exercise 1.6.56

$f(x)=4 \times10^{9}|x−(5 \times 10^9)|+2 \times10^9$

Extensions

For the following exercises, solve the inequality.

Exercise 1.6.57

$|−2x− \frac{2}{3}(x+1)|+3>−1$

Answer:: $(−\infty,\infty)$

Exercise 1.6.58

If possible, find all values of $a$ such that there are no x-intercepts for $f(x)=2|x+1|+a$.

Exercise 1.6.59

If possible, find all values of $a$ such that there are no y-intercepts for $f(x)=2|x+1|+a$.

Answer:: There is no solution for a that will keep the function from having a y-intercept. The absolute value function always crosses the y-intercept when $x=0$.

Real-World Applications

Exercise 1.6.60

Cities A and B are on the same east-west line. Assume that city A is located at the origin. If the distance from city A to city B is at least 100 miles and $x$ represents the distance from city B to city A, express this using absolute value notation.

Exercise 1.6.61

The true proportion $p$ of people who give a favorable rating to Congress is 8% with a margin of error of 1.5%. Describe this statement using an absolute value equation.

Answer:: $|p−0.08|\leq0.015$

Exercise 1.6.62

Students who score within 18 points of the number 82 will pass a particular test. Write this statement using absolute value notation and use the variable $x$ for the score.

Exercise 1.6.63

A machinist must produce a bearing that is within 0.01 inches of the correct diameter of 5.0 inches. Using $x$ as the diameter of the bearing, write this statement using absolute value notation.

Answer:: $|x−5.0|\leq0.01$

Exercise 1.6.64

The tolerance for a ball bearing is 0.01. If the true diameter of the bearing is to be 2.0 inches and the measured value of the diameter is $x$ inches, express the tolerance using absolute value notation.