1.7E: Exercises

Last updated
Save as PDF

Page ID: 31074

This page is a draft and is under active development.

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Section Exercises

Verbal

Exercise 1.7.1

Describe why the horizontal line test is an effective way to determine whether a function is one-to-one?

Answer:: Each output of a function must have exactly one output for the function to be one-to-one. If any horizontal line crosses the graph of a function more than once, that means that $y$-values repeat and the function is not one-to-one. If no horizontal line crosses the graph of the function more than once, then no $y$-values repeat and the function is one-to-one.

Exercise 1.7.2

Why do we restrict the domain of the function $f(x)=x^2$ to find the function’s inverse?

Exercise 1.7.3

Can a function be its own inverse? Explain.

Answer:: Yes. For example, $f(x)=\frac{1}{x}$ is its own inverse.

Exercise 1.7.4

Are one-to-one functions either always increasing or always decreasing? Why or why not?

Exercise 1.7.5

How do you find the inverse of a function algebraically?

Answer:: Given a function $y=f(x)$, solve for $x$ in terms of $y$. Interchange the $x$ and $y$. Solve the new equation for $y$. The expression for $y$ is the inverse, $y=f^{-1}(x)$.

Algebraic

Exercise 1.7.6

Show that the function $f(x)=a−x$ is its own inverse for all real numbers $a$.

For the following exercises, find $f^{-1}(x)$ for each function.

Exercise 1.7.7

$f(x)=x+3$

Answer:: $f^{-1}(x)=x−3$

Exercise 1.7.8

$f(x)=x+5$

Exercise 1.7.9

$f(x)=2−x$

Answer:: $f^{-1}(x)=2−x$

Exercise 1.7.10:

$f(x)=3−x$

Exercise 1.7.11

$f(x)=\frac{x}{x+2}$

Answer:: $f^{-1}(x)=\frac{−2x}{x−1}$

Exercise 1.7.12

$f(x)=\frac{2x+3}{5x+4}$

For the following exercises, find a domain on which each function $f$ is one-to-one and non-decreasing. Write the domain in interval notation. Then find the inverse of $f$ restricted to that domain.

Exercise 1.7.13

$f(x)=(x+7)^2$

Answer:: domain of $f(x)$: $\left[−7,\infty\right)$; $f^{-1}(x)=\sqrt{x}−7$

Exercise 1.7.14

$f(x)=(x−6)^2$

Exercise 1.7.15

$f(x)=x^2−5$

Answer:: domain of $f(x)$: $\left[0,\infty\right)$; $f^{-1}(x)=\sqrt{x+5}$

Exercise 1.7.16

Given $f(x)=\frac{x}{2+x}$ and $g(x)=\frac{2x}{1-x}:$

a. Find $f(g(x))$ and $g(f(x))$.

b. What does the answer tell us about the relationship between $f(x)$ and $g(x)?$

Answer:: a. $f(g(x))=x$ and $g(f(x))=x$.

b. This tells us that $f$ and $g$ are inverse functions

For the following exercises, use function composition to verify that $f(x)$ and $g(x)$ are inverse functions.

Exercise 1.7.17

$f(x)=\sqrt[3]{x-1}$ and $g(x)=x^3+1$

Answer:: $f(g(x))=x$, $g(f(x))=x$

Exercise 1.7.18

$f(x)=−3x+5$ and $g(x)=\frac{x-5}{-3}$

Graphical

For the following exercises, use a graphing utility to determine whether each function is one-to-one.

Exercise 1.7.19

$f(x)=\sqrt{x}$

Answer:: one-to-one

Exercise 1.7.20

$f(x)=\sqrt[3]{3x+1}$

Exercise 1.7.21

$f(x)=−5x+1$

Answer:: one-to-one

Exercise 1.7.22

$f(x)=x^3−27$

For the following exercises, determine whether the graph represents a one-to-one function.

Exercise 1.7.23

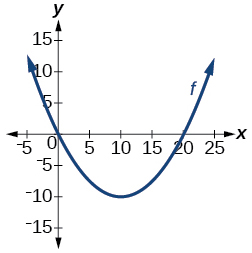
$Graph of a parabola.$

Answer:: not one-to-one

Exercise 1.7.24

$Graph of a step-function.$

For the following exercises, use the graph of $f$ shown in Figure 1.7.11.

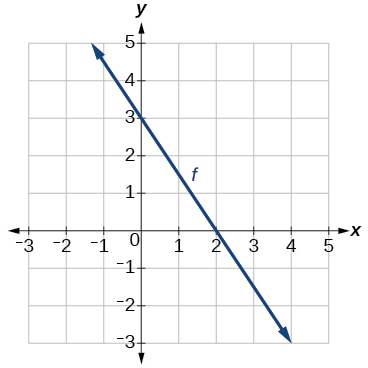
$Graph of a line.$

Figure 1.7.11: Graph of a line

Exercise 1.7.25

Find $f(0)$.

Answer:: 3

Exercise 1.7.26

Solve $f(x)=0$.

Exercise 1.7.27

Find $f^{-1}(0)$.

Answer:: 2

Exercise 1.7.28

Solve $f^{-1}(x)=0$.

For the following exercises, use the graph of the one-to-one function shown in Figure 1.7.12.

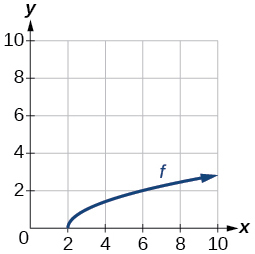
$Graph of a square root function.$
Figure 1.7.12: Graph of a square root function.

Exercise 1.7.29

Sketch the graph of $f^{-1}$.

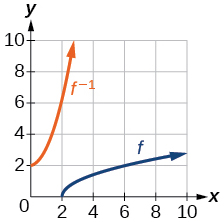
Answer:: $Graph of a square root function and its inverse.$

Exercise 1.7.30

Find $f(6)$ and $f^{-1}(2)$.

Exercise 1.7.31

If the complete graph of $f$ is shown, find the domain of $f$.

Answer:: $[2,10]$

Exercise 1.7.32

If the complete graph of $f$ is shown, find the range of $f$

Numeric

For the following exercises, evaluate or solve, assuming that the function $f$ is one-to-one.

Exercise 1.7.33

If $f(6)=7$, find $f^{-1}(7)$.

Answer:: 6

Exercise 1.7.34

If $f(3)=2$, find $f^{-1}(2)$.

Exercise 1.7.35

If $f^{-1}(−4)=−8$, find $f(−8)$.

Answer:: -4

Exercise 1.7.36

If $f^{-1}(−2)$=−1, find $f(−1)$.

For the following exercises, use the values listed in Table 1.7.6 to evaluate or solve.

$x$	$f(x)$
0	8
1	0
2	7
3	4
4	2
5	6
6	5
7	3
8	9
9	1

Table 1.7.6

Exercise 1.7.37

Find $f(1)$.

Answer:: 0

Exercise 1.7.38

Solve $f(x)=3$.

Exercise 1.7.39

Find $f^{-1}(0)$.

Answer:: 1

Exercise 1.7.40

Solve $f^{-1}(x)=7$.

Exercise 1.7.41

Use the tabular representation of $f$ in Table 1.7.7 to create a table for f^{-1}(x).

$x$	3	6	9	13	14
$f(x)$	1	4	7	12	16

Table 1.7.7

Answer:

$x$	1	4	7	12	16
$f^{-1}(x)$	3	6	9	13	14

Technology

For the following exercises, find the inverse function. Then, graph the function and its inverse.

Exercise 1.7.42

$f(x)=\dfrac{3}{x-2}$

Exercise 1.7.43

$f(x)=x^3−1$

Answer:

$f^{-1}(x)=(1+x)^{1/3}$

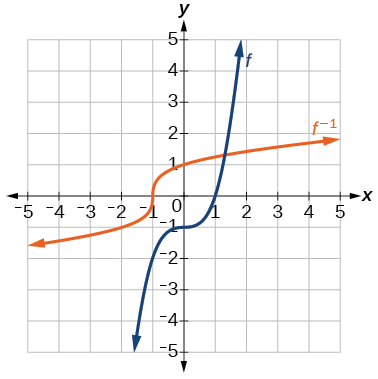
$Graph of a cubic function and its inverse.$

Exercise 1.7.44

Find the inverse function of $f(x)=\frac{1}{x-1}$. Use a graphing utility to find its domain and range. Write the domain and range in interval notation.

Real-World Applications

Exercise 1.7.45

To convert from $x$ degrees Celsius to $y$ degrees Fahrenheit, we use the formula $f(x)=\frac{9}{5}x+32$. Find the inverse function, if it exists, and explain its meaning.

Answer:: $f^{-1}(x)=\frac{5}{9}(x−32)$. Given the Fahrenheit temperature, $x$, this formula allows you to calculate the Celsius temperature.

Exercise 1.7.46

The circumference $C$ of a circle is a function of its radius given by $C(r)=2{\pi}r$. Express the radius of a circle as a function of its circumference. Call this function $r(C)$. Find $r(36\pi)$ and interpret its meaning.

Exercise 1.7.47

A car travels at a constant speed of 50 miles per hour. The distance the car travels in miles is a function of time, $t$, in hours given by $d(t)=50t$. Find the inverse function by expressing the time of travel in terms of the distance traveled. Call this function $t(d)$. Find $t(180)$ and interpret its meaning.

Answer:: $t(d)=\frac{d}{50}$, $t(180)=\frac{180}{50}$. The time for the car to travel 180 miles is 3.6 hours.

\(x\)	\(f(x)\)
0	8
1	0
2	7
3	4
4	2
5	6
6	5
7	3
8	9
9	1

\(x\)	3	6	9	13	14
\(f(x)\)	1	4	7	12	16

\(x\)	1	4	7	12	16
\(f^{-1}(x)\)	3	6	9	13	14