2.4: Infinite Limits

Last updated

Jan 18, 2022
Save as PDF
- 2.3E: Exercises for Section 2.3
- 2.4E: Exercises for Section 2.4

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Infinite Limits

Evaluating the limit of a function at a point or evaluating the limit of a function from the right and left at a point helps us to characterize the behavior of a function around a given value. As we shall see, we can also describe the behavior of functions that do not have finite limits.

We now turn our attention to $h(x)=1/(x−2)^2$ , the third and final function introduced at the beginning of this section (see Figure $\PageIndex{1}$ (c)). From its graph we see that as the values of $x$ approach $2$ , the values of $h(x)=1/(x−2)^2$ become larger and larger and, in fact, become infinite. Mathematically, we say that the limit of $h(x)$ as $x$ approaches $2$ is positive infinity. Symbolically, we express this idea as

$\lim_{x \to 2}h(x)=+∞. \nonumber$

More generally, we define infinite limits as follows:

Definitions: Infinite Limits

We define three types of infinite limits.

Infinite limits from the left: Let $f(x)$ be a function defined at all values in an open interval of the form $(b,a)$ .

i. If the values of $f(x)$ increase without bound as the values of $x$ (where $x<a$ ) approach the number $a$ , then we say that the limit as $x$ approaches $a$ from the left is positive infinity and we write $\lim_{x \to a^−}f(x)=+∞.$

ii. If the values of $f(x)$ decrease without bound as the values of $x$ (where $x<a$ ) approach the number $a$ , then we say that the limit as $x$ approaches $a$ from the left is negative infinity and we write $\lim_{x \to a^−}f(x)=−∞.$

Infinite limits from the right: Let $f(x)$ be a function defined at all values in an open interval of the form $(a,c)$ .

i. If the values of $f(x)$ increase without bound as the values of $x$ (where $x>a$ ) approach the number $a$ , then we say that the limit as $x$ approaches $a$ from the left is positive infinity and we write $\lim_{x \to a^+}f(x)=+∞.$

ii. If the values of $f(x)$ decrease without bound as the values of $x$ (where $x>a$ ) approach the number $a$ , then we say that the limit as $x$ approaches $a$ from the left is negative infinity and we write $\lim_{x \to a^+}f(x)=−∞.$

Two-sided infinite limit: Let $f(x)$ be defined for all $x≠a$ in an open interval containing $a$

i. If the values of $f(x)$ increase without bound as the values of $x$ (where $x≠a$ ) approach the number $a$ , then we say that the limit as $x$ approaches $a$ is positive infinity and we write $\lim_{x \to a} f(x)=+∞.$

ii. If the values of $f(x)$ decrease without bound as the values of $x$ (where $x≠a$ ) approach the number $a$ , then we say that the limit as $x$ approaches $a$ is negative infinity and we write $\lim_{x \to a}f(x)=−∞.$

It is important to understand that when we write statements such as $\displaystyle \lim_{x \to a}f(x)=+∞$ or $\displaystyle \lim_{x \to a}f(x)=−∞$ we are describing the behavior of the function, as we have just defined it. We are not asserting that a limit exists. For the limit of a function $f(x)$ to exist at $a$ , it must approach a real number $L$ as $x$ approaches $a$ . That said, if, for example, $\displaystyle \lim_{x \to a}f(x)=+∞$ , we always write $\displaystyle \lim_{x \to a}f(x)=+∞$ rather than $\displaystyle \lim_{x \to a}f(x)$ DNE.

Example $\PageIndex{5}$ : Recognizing an Infinite Limit

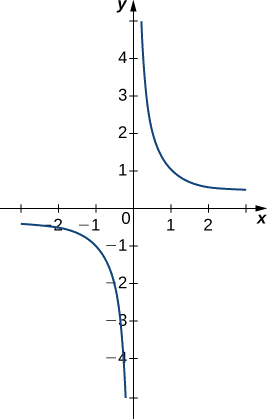
Evaluate each of the following limits, if possible. Use a table of functional values and graph $f(x)=1/x$ to confirm your conclusion.

$\displaystyle \lim_{x \to 0^−} \frac{1}{x}$
$\displaystyle \lim_{x \to 0^+} \frac{1}{x}$
$\displaystyle \lim_{x \to 0}\frac{1}{x}$

Solution

Begin by constructing a table of functional values.

Table $\PageIndex{7}$
$x$	$\dfrac{1}{x}$	$x$	$\dfrac{1}{x}$
-0.1	-10	0.1	10
-0.01	-100	0.01	100
-0.001	-1000	0.001	1000
-0.0001	-10,000	0.0001	10,000
-0.00001	-100,000	0.00001	100,000
-0.000001	-1,000,000	0.000001	1,000,000

a. The values of $1/x$ decrease without bound as $x$ approaches $0$ from the left. We conclude that

$\lim_{x \to 0^−}\frac{1}{x}=−∞.\nonumber$

b. The values of $1/x$ increase without bound as $x$ approaches $0$ from the right. We conclude that

$\lim_{x \to 0^+}\frac{1}{x}=+∞. \nonumber$

c. Since $\displaystyle \lim_{x \to 0^−}\frac{1}{x}=−∞$ and $\displaystyle \lim_{x \to 0^+}\frac{1}{x}=+∞$ have different values, we conclude that

$\lim_{x \to 0}\frac{1}{x}\quad\text{DNE.} \nonumber$

The graph of $f(x)=1/x$ in Figure $\PageIndex{8}$ confirms these conclusions.

The graph of the function f(x) = 1/x. The function curves asymptotically towards x=0 and y=0 in quadrants one and three. — Figure $\PageIndex{8}$ : The graph of $f(x)=1/x$ confirms that the limit as $x$ approaches $0$ does not exist.

Exercise $\PageIndex{5}$

Evaluate each of the following limits, if possible. Use a table of functional values and graph $f(x)=1/x^2$ to confirm your conclusion.

$\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}$
$\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}$
$\displaystyle \lim_{x \to 0}\frac{1}{x^2}$

Hint

Follow the procedures from Example $\PageIndex{4}$ .

Answer

a. $\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}=+∞$ ;

b. $\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}=+∞$ ;

c. $\displaystyle \lim_{x \to 0}\frac{1}{x^2}=+∞$

It is useful to point out that functions of the form

$f(x)=1/(x−a)^n$ , where n is a positive integer, have infinite limits as

$x$ approaches

$a$ from either the left or right (Figure

$\PageIndex{9}$ ). These limits are summarized in the above definitions.

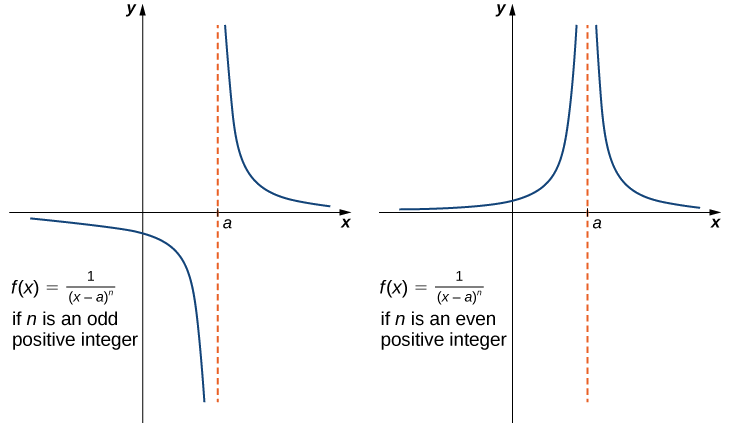
Two graphs side by side of f(x) = 1 / (x-a)^n. The first graph shows the case where n is an odd positive integer, and the second shows the case where n is an even positive integer. In the first, the graph has two segments. Each curve asymptotically towards the x axis, also known as y=0, and x=a. The segment to the left of x=a is below the x axis, and the segment to the right of x=a is above the x axis. In the second graph, both segments are above the x axis. — Figure $\PageIndex{9}$ : The function $f(x)=1/(x−a)^n$ has infinite limits at $a$ .

Infinite Limits from Positive Integers

If $n$ is a positive even integer, then

$\lim_{x \to a}\frac{1}{(x−a)^n}=+∞.\label{infLim1}$

If $n$ is a positive odd integer, then

$\lim_{x \to a^+}\frac{1}{(x−a)^n}=+∞\label{infLim2}$

and

$\lim_{x \to a^−}\frac{1}{(x−a)^n}=−∞.\label{infLim3}$

We should also point out that in the graphs of $f(x)=1/(x−a)^n$ , points on the graph having $x$ -coordinates very near to a are very close to the vertical line $x=a$ . That is, as $x$ approaches $a$ , the points on the graph of $f(x)$ are closer to the line $x=a$ . The line $x=a$ is called a vertical asymptote of the graph. We formally define a vertical asymptote as follows:

Definition: Vertical Asymptotes

Let $f(x)$ be a function. If any of the following conditions hold, then the line $x=a$ is a vertical asymptote of $f(x)$ .

$\lim_{x \to a^−}f(x)=+∞$

$\lim_{x \to a^−}f(x)=−∞$

$\lim_{x \to a^+}f(x)=+∞$

$\lim_{x \to a^+}f(x)=−∞$

$\lim_{x \to a}f(x)=+∞$

$\lim_{x \to a}f(x)=−∞$

Example $\PageIndex{6}$ : Finding a Vertical Asymptote

Evaluate each of the following limits using Equations $\ref{infLim1}$ , $\ref{infLim2}$ , and $\ref{infLim3}$ above. Identify any vertical asymptotes of the function $f(x)=1/(x+3)^4.$

$\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}$
$\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}$
$\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}$

Solution

We can use the above equations directly.

$\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}=+∞$
$\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}=+∞$
$\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}=+∞$

The function $f(x)=1/(x+3)^4$ has a vertical asymptote of $x=−3$ .

Exercise $\PageIndex{6}$

Evaluate each of the following limits. Identify any vertical asymptotes of the function $f(x)=\dfrac{1}{(x−2)^3}$ .

$\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}$
$\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}$
$\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}$

Answer a: $\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}=−∞$
Answer b: $\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}=+∞$
Answer c: $\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}$ DNE. The line $x=2$ is the vertical asymptote of $f(x)=1/(x−2)^3.$

In the next example we put our knowledge of various types of limits to use to analyze the behavior of a function at several different points.

Example $\PageIndex{7}$ : Behavior of a Function at Different Points

Use the graph of $f(x)$ in Figure $\PageIndex{10}$ to determine each of the following values:

$\displaystyle \lim_{x \to −4^−}f(x)$ ; $\displaystyle \lim_{x \to −4^+}f(x)$ ; $\displaystyle \lim_{x→−4}f(x);\;f(−4)$
$\displaystyle \lim_{x \to −2^−}f(x$ ); $\displaystyle \lim_{x \to −2^+}f(x)$ ; $\displaystyle \lim_{x→−2}f(x);\;f(−2)$
$\displaystyle \lim_{x \to 1^−}f(x)$ ; $\displaystyle \lim_{x \to 1^+}f(x)$ ; $\displaystyle \lim_{x \to 1}f(x);\;f(1)$
$\displaystyle \lim_{x \to 3^−}f(x)$ ; $\displaystyle \lim_{x \to 3^+}f(x)$ ; $\displaystyle \lim_{x \to 3}f(x);\;f(3)$

The graph of a function f(x) described by the above limits and values. There is a smooth curve for values below x=-2; at (-2, 3), there is an open circle. There is a smooth curve between (-2, 1] with a closed circle at (1,6). There is an open circle at (1,3), and a smooth curve stretching from there down asymptotically to negative infinity along x=3. The function also curves asymptotically along x=3 on the other side, also stretching to negative infinity. The function then changes concavity in the first quadrant around y=4.5 and continues up. — Figure $\PageIndex{10}$ : The graph shows $f(x)$ .

Solution

Using the definitions above and the graph for reference, we arrive at the following values:

$\displaystyle \lim_{x \to −4^−}f(x)=0$ ; $\displaystyle \lim_{x \to −4^+}f(x)=0$ ; $\displaystyle \lim_{x \to −4}f(x)=0;\;f(−4)=0$
$\displaystyle \lim_{x \to −2^−}f(x)=3$ ; $\displaystyle \lim_{x \to −2^+}f(x)=3$ ; $\displaystyle \lim_{x \to −2}f(x)=3;\;f(−2)$ is undefined
$\displaystyle \lim_{x \to 1^−}f(x)=6$ ; $\displaystyle \lim_{x \to 1^+}f(x)=3$ ; $\displaystyle \lim_{x \to 1}f(x)$ DNE; $f(1)=6$
$\displaystyle \lim_{x \to 3^−}f(x)=−∞$ ; $\displaystyle \lim_{x \to 3^+}f(x)=−∞$ ; $\displaystyle \lim_{x \to 3}f(x)=−∞$ ; $f(3)$ is undefined

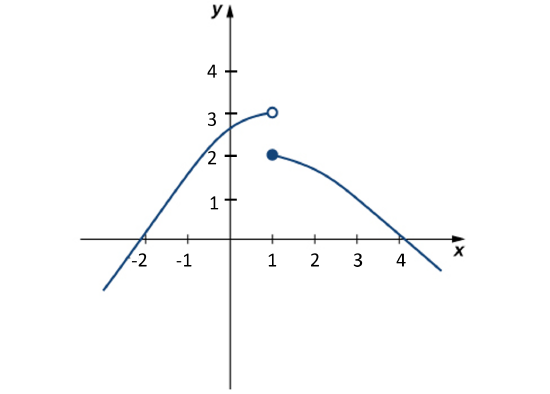
Exercise $\PageIndex{7}$

Evaluate $\displaystyle\lim_{x \to 1}f(x)$ for $f(x)$ shown here:

The graph of a piecewise function. The first segment curves from the third quadrant to the first, crossing through the second quadrant. Where the endpoint would be in the first quadrant is an open circle. The second segment starts at a closed circle a few units below the open circle. It curves down from quadrant one to quadrant four. — Figure $\PageIndex{11}$ . The graph of a piecewise function $f$ .

Hint: Compare the limit from the right with the limit from the left.
Answer: $\displaystyle\lim_{x \to 1}f(x)$ does not exist

Example $\PageIndex{8}$ : Einstein’s Equation

In the Chapter opener we mentioned briefly how Albert Einstein showed that a limit exists to how fast any object can travel. Given Einstein’s equation for the mass of a moving object

$m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber$

what is the value of this bound?

A picture of a futuristic spaceship speeding through deep space. — Figure $\PageIndex{12}$ . (Crefit:NASA)

Solution

Our starting point is Einstein’s equation for the mass of a moving object,

$m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber$

where $m_0$ is the object’s mass at rest, $v$ is its speed, and $c$ is the speed of light. To see how the mass changes at high speeds, we can graph the ratio of masses $m/m_0$ as a function of the ratio of speeds, $v/c$ (Figure $\PageIndex{13}$ ).

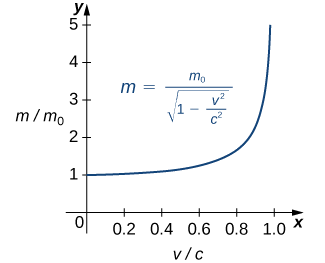
A graph showing the ratio of masses as a function of the ratio of speed in Einstein’s equation for the mass of a moving object. The x axis is the ratio of the speeds, v/c. The y axis is the ratio of the masses, m/m0. The equation of the function is m = m0 / sqrt(1 – v2 / c2 ). The graph is only in quadrant 1. It starts at (0,1) and curves up gently until about 0.8, where it increases seemingly exponentially; there is a vertical asymptote at v/c (or x) = 1. — Figure $\PageIndex{13}$ : This graph shows the ratio of masses as a function of the ratio of speeds in Einstein’s equation for the mass of a moving object.

We can see that as the ratio of speeds approaches 1—that is, as the speed of the object approaches the speed of light—the ratio of masses increases without bound. In other words, the function has a vertical asymptote at $v/c=1$ . We can try a few values of this ratio to test this idea.

Table $\PageIndex{8}$
$v/c$	$\sqrt{1-\frac{v^2}{c^2}}$	$m/m_o$
0.99	0.1411	7.089
0.999	0.0447	22.37
0.9999	0.0141	70.7

Thus, according to Table $\PageIndex{8}$ :, if an object with mass 100 kg is traveling at 0.9999c, its mass becomes 7071 kg. Since no object can have an infinite mass, we conclude that no object can travel at or more than the speed of light.

We now turn our attention to evaluating a limit of the form $\displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}$ , where $\displaystyle \lim_{x→a}f(x)=K$ , where $K≠0$ and $\displaystyle \lim_{x→a}g(x)=0$ . That is, $f(x)/g(x)$ has the form $K/0,K≠0$ at a.

Example $\PageIndex{9}$ : Evaluating a Limit of the Form $K/0,\,K≠0$ Using the Limit Laws

Evaluate $\displaystyle \lim_{x→2^−}\dfrac{x−3}{x^2−2x}$ .

Solution

Step 1. After substituting in $x=2$ , we see that this limit has the form $−1/0$ . That is, as $x$ approaches $2$ from the left, the numerator approaches $−1$ ; and the denominator approaches $0$ . Consequently, the magnitude of $\dfrac{x−3}{x(x−2)}$ becomes infinite. To get a better idea of what the limit is, we need to factor the denominator:

$\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=\lim_{x→2^−}\dfrac{x−3}{x(x−2)} \nonumber$

Step 2. Since $x−2$ is the only part of the denominator that is zero when 2 is substituted, we then separate $1/(x−2)$ from the rest of the function:

$=\lim_{x→2^−}\dfrac{x−3}{x}⋅\dfrac{1}{x−2} \nonumber$

Step 3. Using the Limit Laws, we can write:

$=\left(\lim_{x→2^−}\dfrac{x−3}{x}\right)\cdot\left(\lim_{x→2^−}\dfrac{1}{x−2}\right). \nonumber$

Step 4. $\displaystyle \lim_{x→2^−}\dfrac{x−3}{x}=−\dfrac{1}{2}$ and $\displaystyle \lim_{x→2^−}\dfrac{1}{x−2}=−∞$ . Therefore, the product of $(x−3)/x$ and $1/(x−2)$ has a limit of $+∞$ :

$\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=+∞. \nonumber$

Exercise $\PageIndex{9}$

Evaluate $\displaystyle \lim_{x→1}\dfrac{x+2}{(x−1)^2}$ .

Solution: Use the methods from Example $\PageIndex{9}$ .

Answer: $+∞$

Search

Text Color

Text Size

Margin Size

Font Type

Infinite Limits from Positive Integers

Infinite Limits

Infinite Limits from Positive Integers

Support Center

How can we help?