5.4.1: Exercises for Section 5.4

1) Consider two athletes running at variable speeds \(v_1(t)\) and \(v_2(t).\) The runners start and finish a race at exactly the same time. Explain why the two runners must be going the same speed at some point.

2) Two mountain climbers start their climb at base camp, taking two different routes, one steeper than the other, and arrive at the peak at exactly the same time. Is it necessarily true that, at some point, both climbers increased in altitude at the same rate?

Answer

Yes. It is implied by the Mean Value Theorem for Integrals.

3) To get on a certain toll road a driver has to take a card that lists the mile entrance point. The card also has a timestamp. When going to pay the toll at the exit, the driver is surprised to receive a speeding ticket along with the toll. Explain how this can happen.

4) Set \(\displaystyle F(x)=∫^x _1(1−t)\,dt.\) Find \( F′(2)\) and the average value of \(F'\) over \([1,2].\)

Answer

\(F′(2)=−1;\) average value of \(F'\) over \( [1,2]\) is \(−1/2.\)

In exercises 5 - 8, use the evaluation theorem to express the integral as a function \(F(x).\)

5) \(\displaystyle ∫^x_at^2\,dt\)

6) \(\displaystyle ∫^x_1e^t\,dt\)

Answer

\(F(x)=e^x−e\)

7) \(\displaystyle ∫^x_0\cos t\,dt\)

8) \(\displaystyle ∫^x_{−x}\sin t\,dt\)

Answer

\(F(x)=0\)

In exercises 9 - 12, identify the roots of the integrand to remove absolute values, then evaluate using the Fundamental Theorem of Calculus, Part 2.

9) \(\displaystyle ∫^3_{−2}|x|\,dx\)

10) \(\displaystyle ∫^4_{−2}∣t^2−2t−3∣\,dt\)

Answer

\(\displaystyle ∫^{−1}_{−2}(t^2−2t−3)\,dt−∫^3_{−1}(t^2−2t−3)\,dt+∫^4_3(t^2−2t−3)\,dt=\frac{46}{3}\)

11) \(\displaystyle ∫^π_0|\cos t|\,dt\)

12) \(\displaystyle ∫^{π/2}_{−π/2}|\sin t|\,dt\)

Answer

\(\displaystyle −∫^0_{−π/2}\sin t\,dt+∫^{π/2}_0\sin t\,dt=2\)

In exercises 13 - 22, use symmetry to evaluate the integral.

13) \(\displaystyle ∫^2_{-2}10x^4\,dx\)

Answer

\(128\)

14) \(\displaystyle ∫^{9}_{-9}-\frac{1}{3}t^7\,dt\)

15) \(\displaystyle ∫^{99}_{-99}x-13x^3+2x^5\,dx\)

Answer

\(0\)

16) \(\displaystyle ∫^{\frac{π}{2}}_{-\frac{π}{2}}\cos{θ}\,dθ\)

17) \(\displaystyle ∫^2_{-2}x^5-3x^4+6x^2+x+3\,dx\)

Answer

\(\frac{28}{5}\)

18) \(\displaystyle ∫^5_{-5}1-12x^3+\frac{x^4}{2}-x^5\,dx\)

Answer

\(635\)

19) \(\displaystyle ∫^{\frac{π}{4}}_{-\frac{π}{4}}2\tan{t}\,dt\)

Answer

\(0\)

20) \(\displaystyle ∫^{\pi}_{-\pi}2\sin{θ}-\theta\,dθ\)

21) \(\displaystyle ∫^{\frac{3π}{4}}_{-\frac{3π}{4}}3\cos{x}+\sin{2x}\,dx\)

Answer

\(3\sqrt{2}\)

22) \(\displaystyle ∫^{\frac{π}{2}}_{-\frac{π}{2}}\sin^3{t}\,dt\)

In exercises 23 - 26, find the average value of the function over the given interval.

23) \(f(x)=2x^3\); \([-1,3]\)

Answer

\(10\)

24) \(f(x)=\cos{x}\); \([-\frac{\pi}{4},\frac{\pi}{4}]\)

25) \(f(x)=\sin{x}\); \([-\frac{\pi}{4},\frac{\pi}{4}]\)

Answer

\(0\)

26) \(f(x)=\frac{1}{\sqrt{x}}\); \([1,9]\)

In exercises 27 - 28, find the point(s) at which the given function is equal to its average value on the given interval.

27) \(f(x)=2x^2-4\); \([-2,4]\)

Answer

\(x=-2\); \(x=2\)

28) \(f(x)=\cos{x}\); \([-\frac{\pi}{2},\frac{\pi}{2}]\)

29) Suppose that the number of hours of daylight on a given day in Seattle is modeled by the function \(−3.75\cos(\frac{πt}{6})+12.25\), with \(t\) given in months and \(t=0\) corresponding to the winter solstice.

a. What is the average number of daylight hours in a year?

b. At which times \(t_1\) and \(t_2\), where \(0≤t_1

c. Write an integral that expresses the total number of daylight hours in Seattle between \(t_1\) and \(t_2\)

d. Compute the mean hours of daylight in Seattle between \(t_1\) and \(t_2\), where \(0≤t_1

30) Suppose the rate of gasoline consumption in the United States can be modeled by a sinusoidal function of the form \((11.21−\cos(\frac{πt}{6}))×10^9\) gal/mo.

a. What is the average monthly consumption, and for which values of \(t\) is the rate at time \(t\) equal to the average rate?

b. What is the number of gallons of gasoline consumed in the United States in a year?

c. Write an integral that expresses the average monthly U.S. gas consumption during the part of the year between the beginning of April \((t=3)\) and the end of September \((t=9).\)

Answer

a. The average is \(11.21×10^9\) since \(\cos(\frac{πt}{6})\) has period 12 and integral 0 over any period. Consumption is equal to the average when \(\cos(\frac{πt}{6})=0\), when \(t=3\), and when \(t=9\).
b. Total consumption is the average rate times duration: \(11.21×12×10^9=1.35×10^{11}\)
c. \(\displaystyle 10^9(11.21−\frac{1}{6}∫^9_3\cos(\frac{πt}{6})\,dt)=10^9(11.21+2π)=11.84x10^9\)

31) Explain why, if \(f\) is continuous over \([a,b],\) there is at least one point \( c∈[a,b]\) such that \(\displaystyle f(c)=\frac{1}{b−a}∫^b_af(t)\,dt.\)

32) Explain why, if \(f\) is continuous over \([a,b]\) and is not equal to a constant, there is at least one point \( M∈[a,b]\) such that \(\displaystyle f(M)=\frac{1}{b−a}∫^b_af(t)\,dt\) and at least one point \(m∈[a,b]\) such that \(\displaystyle f(m)<\frac{1}{b−a}∫^b_af(t)\,dt\).

Answer

If \(f\) is not constant, then its average is strictly smaller than the maximum and larger than the minimum, which are attained over \([a,b]\) by the extreme value theorem.

33) Kepler’s first law states that the planets move in elliptical orbits with the Sun at one focus. The closest point of a planetary orbit to the Sun is called the perihelion (for Earth, it currently occurs around January 3) and the farthest point is called the aphelion (for Earth, it currently occurs around July 4). Kepler’s second law states that planets sweep out equal areas of their elliptical orbits in equal times. Thus, the two arcs indicated in the following figure are swept out in equal times. At what time of year is Earth moving fastest in its orbit? When is it moving slowest? Kepler’s first law states that the planets move in elliptical orbits with the Sun at one focus. The closest point of a planetary orbit to the Sun is called the perihelion (for Earth, it currently occurs around January 3) and the farthest point is called the aphelion (for Earth, it currently occurs around July 4). Kepler’s second law states that planets sweep out equal areas of their elliptical orbits in equal times. Thus, the two arcs indicated in the following figure are swept out in equal times. At what time of year is Earth moving fastest in its orbit? When is it moving slowest?

34) A point on an ellipse with major axis length \(2a\) and minor axis length \(2b\) has the coordinates \((a\cos θ,b\sin θ),\quad 0≤θ≤2π.\)

a. Show that the distance from this point to the focus at \((−c,0)\) is \( d(θ)=a+c\cos θ\), where \(c=\sqrt{a^2−b^2}\).

Use these coordinates to show that the average distance \( \bar{d}\) from a point on the ellipse to the focus at \((−c,0),\) with respect to angle \(θ\), is \(a\).

Answer

a. \( d^2θ=(a\cos θ+c)^2+b^2\sin^2 θ=a^2+c^2\cos^2 θ+2ac\cos θ=(a+c\cos θ)^2;\)
b. \(\displaystyle \bar{d}=\frac{1}{2π}∫^{2π}_0(a+2c\cos θ)\,dθ=a\)

35) As implied earlier, according to Kepler’s laws, Earth’s orbit is an ellipse with the Sun at one focus. The perihelion for Earth’s orbit around the Sun is 147,098,290 km and the aphelion is 152,098,232 km.

a. By placing the major axis along the \(x\)-axis, find the average distance from Earth to the Sun.

b. The classic definition of an astronomical unit (AU) is the distance from Earth to the Sun, and its value was computed as the average of the perihelion and aphelion distances. Is this definition justified?

36) The force of gravitational attraction between the Sun and a planet is \(F(θ)=\dfrac{GmM}{r^2(θ)}\), where \(m\) is the mass of the planet, \(M\) is the mass of the Sun, \(G\) is a universal constant, and \(r(θ)\) is the distance between the Sun and the planet when the planet is at an angle \(θ\) with the major axis of its orbit. Assuming that \(M\), \(m\), and the ellipse parameters \(a\) and \(b\) (half-lengths of the major and minor axes) are given, set up—but do not evaluate—an integral that expresses in terms of \(G,\,m,\,M,\,a,\,b\) the average gravitational force between the Sun and the planet.

Answer

Mean gravitational force \(\displaystyle = \frac{GmM}{2}∫^{2π}_0\frac{1}{(a+2\sqrt{a^2−b^2}\cos θ)^2}\,dθ\).

The displacement from rest of a mass attached to a spring satisfies the simple harmonic motion equation \( x(t)=Acos(ωt−ϕ),\) where \(ϕ\) is a phase constant, \(ω\) is the angular frequency, and \(A\) is the amplitude. Find the average velocity, the average speed (magnitude of velocity), the average displacement, and the average distance from rest (magnitude of displacement) of the mass.

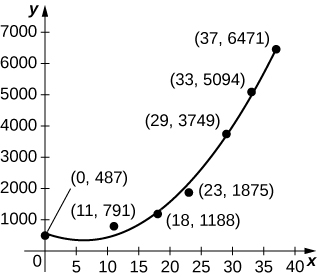
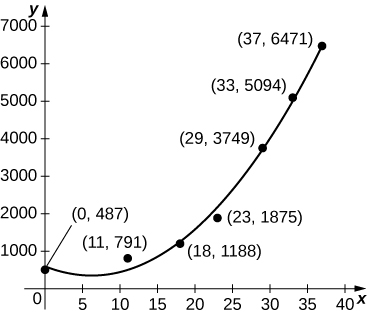
For the next two exercises use the data in the following table, which displays bald eagle populations from 1963 to 2000 in the continental United States.

Year	Population of Breeding Pairs of Bald Eagles
1963	487
1974	791
1981	1188
1986	1875
1992	3749
1996	5094
2000	6471

Population of Breeding Bald Eagle PairsSource: http://www.fws.gov/Midwest/eagle/pop.../chtofprs.html.

37) [T] The graph below plots the quadratic \(p(t)=6.48t^2−80.31t+585.69\) against the data in preceding table, normalized so that \(t=0\) corresponds to 1963. Estimate the average number of bald eagles per year present for the 37 years by computing the average value of \(p\) over \([0,37].\)

38) [T] The graph below plots the cubic \(p(t)=0.07t^3+2.42t^2−25.63t+521.23\) against the data in the preceding table, normalized so that \(t=0\) corresponds to 1963. Estimate the average number of bald eagles per year present for the 37 years by computing the average value of \(p\) over \([0,37].\)

Answer

\(\displaystyle \frac{1}{37}∫^{37}_0p(t)\,dt=\frac{0.07(37)^3}{4}+\frac{2.42(37)^2}{3}−\frac{25.63(37)}{2}+521.23≈2037\)

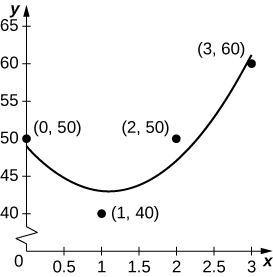
39) [T] Suppose you go on a road trip and record your speed at every half hour, as compiled in the following table. The best quadratic fit to the data is \(q(t)=5x^2−11x+49\), shown in the accompanying graph. Integrate \(q\) to estimate the total distance driven over the 3 hours.

Time (hr)	Speed (m[h)
0 (start)	50
1	40
2	50
3	60

 

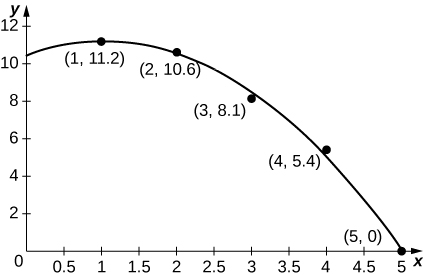
As a car accelerates, it does not accelerate at a constant rate; rather, the acceleration is variable. For the following exercises, use the following table, which contains the acceleration measured at every second as a driver merges onto a freeway.

Time (sec)	Acceleration (mph/sec)
1	11.2
2	10.6
3	8.1
4	5.4
5	0

40) [T] The accompanying graph plots the best quadratic fit, \(a(t)=−0.70t^2+1.44t+10.44\), to the data from the preceding table. Compute the average value of \(a(t)\) to estimate the average acceleration between \(t=0\) and \(t=5.\)

Answer

Average acceleration is \(\displaystyle A=\frac{1}{5}∫^5_0a(t)\,dt=−\frac{0.7(5^2)}{3}+\frac{1.44(5)}{2}+10.44≈8.2\) mph/s

41) [T] Using your acceleration equation from the previous exercise, find the corresponding velocity equation. Assuming the final velocity is 0 mph, find the velocity at time \(t=0.\)

42) [T] Using your velocity equation from the previous exercise, find the corresponding distance equation, assuming your initial distance is 0 mi. How far did you travel while you accelerated your car? (Hint: You will need to convert time units.)

Answer

\(\displaystyle d(t)=∫^1_0|v(t)|\,dt=∫^t_0\left(\frac{7}{30}t^3−0.72t^2−10.44t+41.033\right)\,dt=\frac{7}{120}t^4−0.24t^3−5.22t^3+41.033t.\) Then, \(d(5)≈81.12 \,\text{mph} × \text{sec}≈119\) feet.

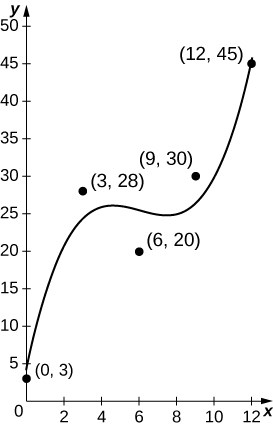
43) [T] The number of hamburgers sold at a restaurant throughout the day is given in the following table, with the accompanying graph plotting the best cubic fit to the data, \(b(t)=0.12t^3−2.13t^3+12.13t+3.91,\) with \(t=0\) corresponding to 9 a.m. and \(t=12\) corresponding to 9 p.m. Compute the average value of \(b(t)\) to estimate the average number of hamburgers sold per hour.

Hours Past Midnight	No. of Burgers Sold
9	3
12	28
15	20
18	30
21	45

44) [T] An athlete runs by a motion detector, which records her speed, as displayed in the following table. The best linear fit to this data, \(ℓ(t)=−0.068t+5.14\), is shown in the accompanying graph. Use the average value of \(ℓ(t)\) between \(t=0\) and \(t=40\) to estimate the runner’s average speed.

Minutes	Speed (m/sec)
0	5
10	4.8
20	3.6
30	3.0
40	2.5

 

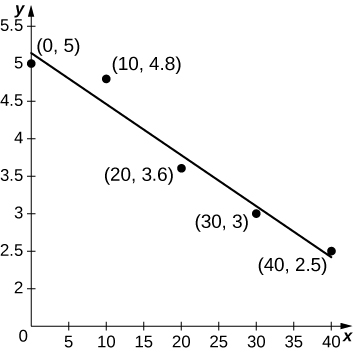
Answer

\(\displaystyle \tfrac{1}{40} ∫^{40}_0(−0.068t+5.14)\,dt=−\frac{0.068(40)}{2}+5.14=3.78\) m/sec