In many areas of Pure and Applied Mathematics, we are interested in finding solutions to an equation of the form \(f(x)=0\). For most functions, however, it is difficult - if not impossible - to calculate their zeros explicitly. In this section, we look at a technique that provides a very efficient way of approximating the zeros of functions. This technique uses tangent line approximations, which most calculators and computers use to find zeros.
Describing Newton’s Method
Consider the task of finding the solutions of \(f(x)=0\). If \(f\) is the first-degree polynomial \(f(x)=ax+b\), then the solution of \(f(x)=0\) is given by the formula \(x=−\frac{b}{a}\). If \(f\) is the second-degree polynomial \(f(x)=ax^2+bx+c\), the solutions of \(f(x)=0\) can be found by using the Quadratic Formula. However, for polynomials of degree 3 or more, finding roots of \(f\) becomes more complicated. Although formulas exist for third- and fourth-degree polynomials, they are quite complicated. Also, if \( f \) is a polynomial of degree 5 or greater, it is known that no such formulas exist. For example, consider the function\[f(x)=x^5+8x^4+4x^3−2x−7.\nonumber \]No formula exists that allows us to find the solutions of \(f(x)=0\). Similar difficulties exist for non-polynomial functions. For example, consider finding solutions of \(\tan(x)−x=0\). No simple formula exists for the solutions of this equation. We can use Newton's Method to approximate the roots in such cases.
Newton's Method makes use of the following idea to approximate the solutions of \(f(x)=0\). By sketching a graph of \(f\), we can estimate a root of \(f(x)=0\). Let's call this estimate \(x_0\). We then draw the tangent line to \(f\) at \(x_0\). If \(f^{\prime}(x_0) \neq 0\), this tangent line intersects the \(x\)-axis at some point \((x_1,0)\). Now, let \(x_1\) be the next approximation to the actual root. Typically, \(x_1\) is closer than \(x_0\) to an actual root. Next, we draw the tangent line to \(f\) at \(x_1\). If \(f^{\prime}(x_1) \neq 0\), this tangent line also intersects the \(x\)-axis, producing another approximation, \(x_2\). We continue in this way, deriving a list of approximations: \(x_0\), \(x_1\), \(x_2\), \(\ldots\). Typically, the numbers \(x_0\), \(x_1\), \(x_2\), \(\ldots\) quickly approach an actual root \(x^*\), as shown in the following figure.

Figure \(\PageIndex{1}\):The approximations \(x_0,\, x_1,\, x_2,\, \ldots \) approach the actual root \(x^*\). The approximations are derived by looking at tangent lines to the graph of \(f\).
Now let’s look at how to calculate the approximations \(x_0\), \(x_1\), \(x_2\), \(\ldots\). If \(x_0\) is our first approximation, the approximation \(x_1\) is defined by letting \((x_1,0)\) be the \(x\)-intercept of the tangent line to \(f\) at \(x_0\). The equation of this tangent line is given by\[y=f(x_0)+f^{\prime}(x_0)(x−x_0). \nonumber \]Therefore, \(x_1\) must satisfy\[f(x_0)+f^{\prime}(x_0)(x_1−x_0)=0.\nonumber \]Solving this equation for \(x_1\), we conclude that\[x_1=x_0−\dfrac{f(x_0)}{f^{\prime}(x_0)}.\nonumber \]Similarly, the point \((x_2,0)\) is the \(x\)-intercept of the tangent line to \(f\) at \(x_1\). Therefore, \(x_2\) satisfies the equation\[x_2=x_1−\dfrac{f(x_1)}{f^{\prime}(x_1)}.\nonumber \]In general, for \(n>0,x_n\) satisfies\[x_n=x_{n−1}−\dfrac{f(x_{n−1})}{f^{\prime}(x_{n−1})}.\label{Newton} \]Next, we see how to make use of this technique to approximate the root of the polynomial \(f(x)=x^3−3x+1\).
Example \(\PageIndex{1}\)
Use Newton’s Method to approximate a root of \(f(x)=x^3−3x+1\) in the interval \([1,2]\). Let \(x_0=2\) and find \(x_1\), \(x_2\), \(x_3\), \(x_4\), and \(x_5\).
- Solution
-
From Figure \(\PageIndex{2}\), we see that \(f\) has one root over the interval \([1,2]\). Therefore, \(x_0=2\) seems like a reasonable first approximation. To find the next approximation, we use Equation \ref{Newton}. Since \(f(x)=x^3−3x+1\), the derivative is \(f^{\prime}(x)=3x^2−3\). Using Equation \ref{Newton} with \(n=1\) (and a calculator that displays \(10\) digits), we obtain\[x_1=x_0−\dfrac{f(x_0)}{f^{\prime}(x_0)}=2−\dfrac{f(2)}{f^{\prime}(2)}=2−\dfrac{3}{9} \approx 1.666666667.\nonumber \]To find the next approximation, \(x_2\), we use Equation \ref{Newton} with \(n=2\) and the value of \(x_1\) stored on the calculator. We find that\[x_2=x_1-\dfrac{f(x_1)}{f^{\prime}(x_1)} \approx 1.548611111.\nonumber \]Continuing in this way, we obtain the following results:
- \(x_1 \approx 1.666666667\)
- \(x_2 \approx 1.548611111\)
- \(x_3 \approx 1.532390162\)
- \(x_4 \approx 1.532088989\)
- \(x_5 \approx 1.532088886\)
- \(x_6 \approx 1.532088886\).
We note that we obtained the same value for \(x_5\) and \(x_6\). Therefore, any subsequent application of Newton's Method will likely give the same value for \(x_n\).

Figure \(\PageIndex{2}\): The function \(f(x)=x^3−3x+1\) has one root over the interval \([1,2]\).
Checkpoint \(\PageIndex{1}\)
Letting \(x_0=0\), let's use Newton's Method to approximate the root of \(f(x)=x^3−3x+1\) over the interval \([0,1]\) by calculating \(x_1\) and \(x_2\).
- Answer
-
\(x_1 \approx 0.33333333\)
\(x_2 \approx 0.347222222\)
Newton's Method can also approximate square roots. Here we show how to approximate \(\sqrt{2}\). This method can be modified to approximate the square root of any positive number.
Example \(\PageIndex{2}\)
Use Newton’s Method to approximate \(\sqrt{2}\) (Figure \(\PageIndex{3}\)). Let \(f(x)=x^2−2\), let \(x_0=2\), and calculate \(x_1\), \(x_2\), \(x_3\), \(x_4\), and \(x_5\). (We note that since \(f(x)=x^2−2\) has a zero at \(\sqrt{2}\), the initial value \(x_0=2\) is a reasonable choice to approximate \(\sqrt{2}\)).

Figure \(\PageIndex{3}\): We can use Newton’s Method to find \(\sqrt{2}\).
- Solution
-
For \(f(x)=x^2−2\), \(f^{\prime}(x)=2x\). From Equation \ref{Newton}, we know that\[\begin{array}{rcl}
x_n & = & x_{n−1}−\dfrac{f(x_{n−1})}{f^{\prime}(x_{n−1})}\\[6pt]
& = & x_{n−1}−\dfrac{x^2_{n−1}−2}{2x_{n−1}}\\[6pt]
& = & \dfrac{1}{2}x_{n−1}+\dfrac{1}{x_{n−1}}\\[6pt]
& = & \dfrac{1}{2}\left(x_{n−1}+\dfrac{2}{x_{n−1}}\right). \\[6pt]
\end{array} \nonumber \]Therefore,\[x_1=\dfrac{1}{2}\left(x_0+\frac{2}{x_0}\right)=\dfrac{1}{2}\left(2+\frac{2}{2}\right)=1.5\nonumber\]\[x_2=\dfrac{1}{2}\left(x_1+\frac{2}{x_1}\right)=\dfrac{1}{2}\left(1.5+\frac{2}{1.5}\right) \approx 1.416666667.\nonumber\]Continuing in this way, we find that\[\begin{array}{rcl}
x_1 & = & 1.5\\
x_2 & \approx & 1.416666667\\
x_3 & \approx & 1.414215686\\
x_4 & \approx & 1.414213562\\
x_5 & \approx & 1.414213562\\
\end{array} \nonumber \]Since we obtained the same value for \(x_4\) and \(x_5\), it is unlikely that the value \(x_n\) will change on any subsequent application of Newton's Method. We conclude that \(\sqrt{2} \approx 1.414213562\).
Checkpoint \(\PageIndex{2}\)
Use Newton’s Method to approximate \(\sqrt{3}\) by letting \(f(x)=x^2−3\) and \(x_0=3\). Find \(x_1\) and \(x_2\).
- Answer
-
\(x_1=2\)
\(x_2=1.75\)
When using Newton's Method, each approximation after the initial guess is defined in terms of the previous approximation by using the same formula. In particular, by defining the function \(F(x)=x−\left[\frac{f(x)}{f^{\prime}(x)}\right]\), we can rewrite Equation \ref{Newton} as \(x_n=F(x_{n−1})\). This type of process, where each \(x_n\) is defined in terms of \(x_{n−1}\) by repeating the same function, is an example of an iterative process. Shortly, we examine other iterative processes. First, let's look at why Newton's Method could fail to find a root.
Failures of Newton’s Method
Typically, Newton's Method finds roots reasonably quickly. However, things can go wrong. Some reasons why Newton's Method might fail include the following:
- At one of the approximations \(x_n\), the derivative \(f^{\prime}\) is zero (or very close to \( 0 \)) at \(x_n\), but \(f(x_n) \neq 0\). As a result, the tangent line of \(f\) at \(x_n\) does not intersect the \(x\)-axis (or, if it does, it is far away from the intended root). Therefore, we cannot continue the iterative process.
- The approximations \(x_0\), \(x_1\), \(x_2\), \(\ldots \) may approach a different root. If the function \(f\) has more than one root, it is possible that our approximations do not approach the one for which we are looking but approach a different root (see Figure \(\PageIndex{4}\)). This event often occurs when we do not choose the approximation \(x_0\) close enough to the desired root.
- The approximations may fail to approach a root entirely. In Example \(\PageIndex{3}\), we provide an example of a function and an initial guess \(x_0\) such that the successive approximations never approach a root because the successive approximations continue to alternate back and forth between two values.
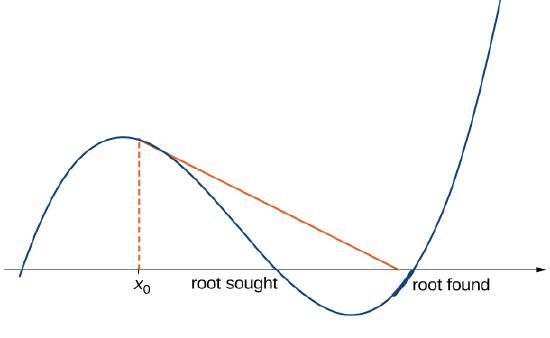
Figure \(\PageIndex{4}\): If the initial guess \(x_0\) is too far from the root sought, it may lead to approximations that approach a different root.
Example \(\PageIndex{3}\)
Consider the function \(f(x)=x^3−2x+2\). Let \(x_0=0\). Show that the sequence \(x_1\), \(x_2\), \(\ldots \) fails to approach a root of \(f\).
- Solution
-
For \(f(x)=x^3−2x+2\), the derivative is \(f^{\prime}(x)=3x^2−2\).Therefore,\[x_1=x_0−\dfrac{f(x_0)}{f^{\prime}(x_0)}=0−\dfrac{f(0)}{f^{\prime}(0)}=−\dfrac{2}{−2}=1. \nonumber \]In the next step,\[x_2=x_1−\dfrac{f(x_1)}{f^{\prime}(x_1)}=1−\dfrac{f(1)}{f^{\prime}(1)}=1−\dfrac{1}{1}=0. \nonumber \]Consequently, the numbers \(x_0,\, x_1,\, x_2,\, \ldots \) continue to bounce back and forth between \(0\) and \(1\) and never get closer to the root of \(f\) which is over the interval \([−2,−1]\) (Figure \(\PageIndex{5}\)). Fortunately, if we choose an initial approximation \(x_0\) closer to the actual root, we can avoid this situation.

Figure \(\PageIndex{5}\): The approximations continue to alternate between \(0\) and \(1\) and never approach the root of \(f\).
Checkpoint \(\PageIndex{3}\)
For \(f(x)=x^3−2x+2\), let \(x_0=−1.5\) and find \(x_1\) and \(x_2\).
- Answer
-
\(x_1 \approx −1.842105263\)
\(x_2 \approx −1.772826920\)
From Example \(\PageIndex{3}\), we see that Newton's Method does not always work. However, when it does work, the sequence of approximations approaches the root very quickly. Discussions of how quickly the sequence of approximations approach a root found using Newton's Method are included in texts on Numerical Analysis.
Other Iterative Processes
As mentioned earlier, Newton's Method is an iterative process. We now look at an example of a different kind of iterative process.
Consider a function \(F\) and an initial number \(x_0\). Define the subsequent numbers \(x_n\) by the formula \(x_n=F(x_{n−1})\). This process is an iterative process that creates a list of numbers \(x_0\), \(x_1\), \(x_2\), \(\ldots\), \(x_n\), \(\ldots \). This list of numbers may approach a finite number \(x^*\) as \(n\) gets larger, or it may not. In Example \(\PageIndex{4}\), we see an example of a function \(F\) and an initial guess \(x_0\) such that the resulting list of numbers approaches a finite value.
Example \(\PageIndex{4}\)
Let \(F(x)=\frac{1}{2}x+4\) and let \(x_0=0\). For all \(n \geq 1\), let \(x_n=F(x_{n−1})\). Find the values \(x_1\), \(x_2\), \(x_3\), \(x_4\), and \(x_5\). Make a conjecture about what happens to this list of numbers \(x_1\), \(x_2\), \(\ldots\), \(x_n\), \(\ldots \) as \(n \to \infty\). If the list of numbers \(x_1\), \(x_2\), \(\ldots\) approaches a finite number \(x^*\), then \(x^*\) satisfies \(x^*=F(x^*)\), and \(x^*\) is called a fixed point of \(F\).
- Solution
-
If \(x_0=0\), then
- \(x_1=\frac{1}{2}(0)+4=4\)
- \(x_2=\frac{1}{2}(4)+4=6\)
- \(x_3=\frac{1}{2}(6)+4=7\)
- \(x_4=\frac{1}{2}(7)+4=7.5\)
- \(x_5=\frac{1}{2}(7.5)+4=7.75\)
- \(x_6=\frac{1}{2}(7.75)+4=7.875\)
- \(x_7=\frac{1}{2}(7.875)+4=7.9375\)
- \(x_8=\frac{1}{2}(7.9375)+4=7.96875\)
- \(x _9=\frac{1}{2}(7.96875)+4=7.984375\).
From this list, we conjecture that the values \(x_n\) approach \(8\).
Figure \(\PageIndex{6}\) provides a graphical argument that the values approach \(8\) as \(n \to \infty\). Starting at the point \((x_0,x_0)\), we draw a vertical line to the point \((x_0,F(x_0))\). The next number in our list is \(x_1=F(x_0)\). We use \(x_1\) to calculate \(x_2\). Therefore, we draw a horizontal line connecting \((x_0,x_1)\) to the point \((x_1,x_1)\) on the line \(y=x\), and then draw a vertical line connecting \((x_1,x_1)\) to the point \((x_1,F(x_1))\). The output \(F(x_1)\) becomes \(x_2\). Continuing in this way, we could create infinite line segments. These line segments are trapped between the lines \(F(x)=\frac{x}{2}+4\) and \(y=x\). The line segments get closer to the intersection point of these two lines, which occurs when \(x=F(x)\). Solving the equation \(x=\frac{x}{2}+4\), we conclude they intersect at \(x=8\). Therefore, our graphical evidence agrees with our numerical evidence that the list of numbers \(x_0,\, x_1,\, x_2,\, \ldots \) approaches \(x^*=8\) as \(n \to \infty\).

Figure \(\PageIndex{6}\): This iterative process approaches the value \(x^*=8\).
Checkpoint \(\PageIndex{4}\)
Consider the function \(F(x)=\frac{1}{3}x+6\). Let \(x_0=0\) and let \(x_n=F(x_{n−1})\) for \(n \geq 2\). Find \(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). Make a conjecture about what happens to the list of numbers \(x_1,\, x_2,\, x_3,\, \ldots \, x_n,\, \ldots \) as \(n \to \infty\).
- Answer
-
\(x_1=6,\;x_2=8,\;x_3=\frac{26}{3},\;x_4=\frac{80}{9},\;x_5=\frac{242}{27};\;x^*=9\)
Iterative Processes and Chaos
Iterative processes can yield some fascinating behavior. In this section, we have seen several examples of iterative processes that converge to a fixed point. We also saw in Example \(\PageIndex{3}\) that the iterative process bounced back and forth between two values. We call this kind of behavior a 2-cycle. Iterative processes can converge to cycles with various periodicities, such as 2−cycles, 4−cycles (where the iterative process repeats a sequence of four values), 8-cycles, and so on.
Some iterative processes yield what mathematicians call chaos. In this case, the iterative process randomly jumps from value to value and never converges nor settles into a cycle. Although a complete exploration of chaos is beyond the scope of this text, in this project we look at one of the key properties of a chaotic iterative process: sensitive dependence on initial conditions. This property refers to the concept that small changes in initial conditions can generate drastically different behavior in the iterative process.
Probably the best-known example of chaos is the Mandelbrot set (see Figure \(\PageIndex{7}\)), named after Benoit Mandelbrot (1924–2010), who investigated its properties and helped popularize the field of chaos theory. The Mandelbrot set is usually generated by computer and shows fascinating details on enlargement, including self-replication of the set. Several colorized versions of the set have been shown in museums and can be found online and in popular books on the subject.

Figure \(\PageIndex{7}\): The Mandelbrot set is a well-known example of a set of points generated by the iterative chaotic behavior of a relatively simple function.
In this project we use the logistic map\[f(x)=rx(1−x) \nonumber \]where \(x \in [0,1]\) and \(r>0\) as the function in our iterative process. The logistic map is a deceptively simple function. Still, depending on the value of \(r\), the resulting iterative process displays some fascinating behavior. It can lead to fixed points, cycles, and even chaos.
To visualize the long-term behavior of the iterative process associated with the logistic map, we will use a cobweb diagram tool. As we did with the iterative process we examined earlier in this section, we first draw a vertical line from the point \((x_0,0)\) to the point \((x_0,f(x_0))=(x_0,x_1)\). We then draw a horizontal line from that point to the point \((x_1,x_1)\), then draw a vertical line to \((x_1,f(x_1))=(x_1,x_2)\), and continue the process until the long-term behavior of the system becomes apparent. Figure \(\PageIndex{8}\) shows the long-term behavior of the logistic map when \(r=3.55\) and \(x_0=0.2\). (The first \(100\) iterations are not plotted.) The long-term behavior of this iterative process is an \(8\)-cycle.

Figure \(\PageIndex{8}\): A cobweb diagram for \(f(x)=3.55x(1−x)\) is presented here. The sequence of values results in an 8-cycle.
- Let \(r=0.5\) and choose \(x_0=0.2\). Either by hand or by using a computer, calculate the first \(10\) values in the sequence. Does the sequence appear to converge? If so, to what value? Does it result in a cycle? If so, what kind of cycle (for example, \(2\)−cycle, \(4\)−cycle.)?
- What happens when \(r=2\)?
- For \(r=3.2\) and \(r=3.5\), calculate the first \(100\) sequence values. Generate a cobweb diagram for each iterative process. (Several free applets that generate cobweb diagrams for the logistic map are available online.) What is the long-term behavior in each of these cases?
- Now let \(r=4\). Calculate the first \(100\) sequence values and generate a cobweb diagram. What is the long-term behavior in this case?
- Repeat the process for \(r=4\), but let \(x_0=0.201\). How does this behavior compare with the behavior for \(x_0=0.2\)?











