1.1.1: Integers

Learning Objectives

By the end of this section, you will be able to: 

• Understand arithmetic with signed numbers
• Simplify numerical expressions with signed numbers

Be Prepared

Before we get started, take this readiness quiz (see the appendix concerning arithmetic!).

1. Evaluate \(2\cdot 2 \).

2. Evaluate \(5+3\).

3. Evaluate \(6\div 2\).

We begin with a brief review of arithmetic with integers i.e. \(\ldots,-3,-2,-1,0,1,2,3, \ldots\)

Any number has a weight and a sign.

Definition \(\PageIndex{1}\)

The magnitude (or weight) of a number is the distance it is from 0 on the number line.

Two numbers are opposites if, on the number line, they are on opposite sides of zero, but the same distance away from zero.

Example \(\PageIndex{2}\)

The magnitude of -5 is 5 and the magnitude of 7 is 7 .

So, −5 is the opposite of 5, and 7 is the opposite of −7 and so on.

Try It \(\PageIndex{3}\)

Find the opposite of

a. \(-3\)

b. \(9\)

Answer

a. \(3\)

b. \(-9\)

Addition

We can add two numbers with the help of a number line.

Example \(\PageIndex{4}\)

Add \(3+4\).

Solution

To add \(3 + 4\), we start with 3 on the number line then move 4 units to the right. We land at 7 which is our answer.

So, \(3+4=7\). Notice that the answer has the same sign as the signs of 3 and 4 (both positive) and its weight comes from adding the weights of 3 and 4.

You always move to the right when you add a positive number.

You always move to the left when you add a negative number (a debt).

Example \(\PageIndex{5}\)

Add \(-10+(-4)\).

Solution

Adding two negative numbers, \(-10+(-4)\) means you are adding a debt of \(\$ 4\) to an already existing debt of \(\$ 10 .\) So, we start at -10 on the number line and move 4 units to the left, to land at \(-14,\) which is the answer.

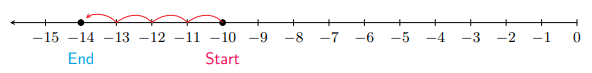
So, \(-10+(-4)=-14\). Notice that the answer has the same sign as the signs of -10 and -4 (both negative) and its weight comes from adding the weights of -10 and -4

To add numbers of opposite signs, that is, a positive and a negative number, we can also use the number line. For example, to perform \(10+(-4),\) we start at 10 on the number line and then move 4 units to the left. We land at \(6,\) which is the answer. Think of \(10+(-4)\) as having \(\$ 10\) and adding a \(\$ 4\) debt. Because we are adding a debt, we move to the left on the number line!

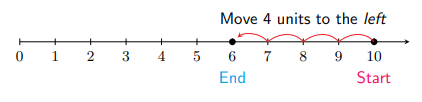
So, \(10+(-4)=6 .\) Notice that the answer has the same sign as the sign of 10 (positive) because it is the number of larger weight, and its weight comes from finding the difference of the weights of 10 and -4

Notice that because we were adding two numbers of opposite signs, the answer ended up being the difference in weight (6) along with the sign of the number of larger weight (positive).

Example \(\PageIndex{6}\)

Add \(3+(-7)\).

Solution

We start at 3 and move toward 7 units to the left, and we land at \(-4,\) which is our answer.

So, \(3+(-7)=-4 .\) Notice that the answer has the same sign as the signs of -7 (negative) because it is the number of larger weight, and its weight comes from finding the difference of the weights of 3 and -7.

Definition \(\PageIndex{7}\)

Two opposite numbers are called a zero-pair, because adding them always results in 0.

Example \(\PageIndex{8}\)

Add \(-5+5\).

Solution

We start at -5 on the number line and jump to the right 5 units to land finally at \(0\). So \(-5+5=0\).

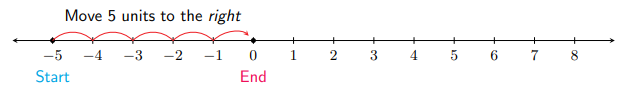
So, −5 and 5 are a zero-pair.

Adding Intergers

1. To add two numbers of the same sign, add their weights and place it after the sign.
2. To add two numbers of opposite signs, find the difference of their weights and place it after the sign of the number with the greater weight.

Example \(\PageIndex{9}\)

Add:

a. \(-8+19\)

b. \(-8+4\)

c. \(6+(-9)\)

d. \(7+(-2)\)

e. \((-4)+(-7)\)

f. \(8+7\)

Solution

a. \(-8+19=11\)

b. \(-8+4=-4\)

c. \(6+(-9)=-3\)

d. \(7+(-2)=5\)

e. \((-4)+(-7)=-11\)

f. \(8+7=15\)

Note

While we can add in any order: \(4+2=2+4\), it is sometimes convenient to add up all of the negative numbers and add up all of the positive numbers, and then add the results. There are also times when it is best to notice certain simplifications if the numbers are added in a different order.

For example

\[-5+4+5+(-8)=-5+(-8)+4+5(\text { by reordering })\nonumber\]

so,

\[−5 + 4 + 5 + (−8) = −5 + (−8) + 4 + 5 = −13 + 9 = −4 \nonumber\]

We could have also simplified this by noting that (-5) and 5 are zero-pair, so we are left with \(4+(-8)\) which is -4.

Example \(\PageIndex{10}\)

Simplify \((-4)+(-5)+7+(-3)\).

Solution

\[(-4)+(-5)+7+(-3)=(-4)+(-5)+(-3)+7=(-12)+7=-5\nonumber\]

We could have simplified this by noting that (-4) and (-3) make -7, and -7 and 7 are zero-pair, so the total is -5.

Try It \(\PageIndex{11}\)

Add:

a. \(9+7\)

b. \(5+(-7)\)

c. \((-4)+(-3)\)

d. \((-4)+2\)

e. \((-4)+8\)

f. \(9+(-3)+7+(-9)+3+5+(-2)\)

Answer

a. \(16\)

b. \(-2\)

c. \(-7\)

d. \(-2\)

e. \(4\)

f. \(10\)

Subtraction (as Addition of the Opposite)

Once we know how to add numbers, we are set to subtract numbers because subtraction is nothing but addition of the opposite. That is, subtracting 8 − 3 (which reads: subtracting 3 from 8) is the same as 8 + (−3) (which reads: Adding −3 to 8.).

Example \(\PageIndex{12}\)

Subtract \(8-3\).

Solution

So, \(8-3=8+(-3),\) and, we can use the rules of adding two numbers of opposite signs to find out that the answer is \(5 .\) We can also use the number line. We start at 8 and move 3 units to the left (adding -3 is adding a debt, so we move to the left). So \(8-3=5\).

Example \(\PageIndex{13}\)

Subtract \(3-7\).

Solution

To calculate \(3-7\) we first rewrite it as an addition problem. \(3-7=3+(-7) .\) We can either use the number line, or the rules of adding two numbers of opposite signs. And, \(50,3-7=3+(-7)=-4\)

Example \(\PageIndex{14}\)

Subtract \(-4-1\).

Solution

To calculate \(-4-1,\) we first rewrite it as an addition problem. \(-4-1=-4+(-1) .\) We can either use the number line, or the rules of adding two numbers of the same signs. If we want to use the rules, both numbers are negative, so our answer will be negative, and, adding the weights of -4 and -1 is \(5.50,-4-1=-4+(-1)=-5\)

On the number line, we start at -4 and move 1 unit to the left, to land on -5 which is our answer.

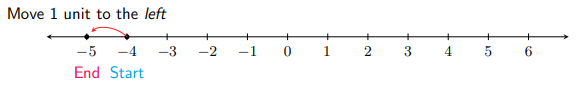
Changing the subtractions to additions in this way is particularly useful when adding or subtracting several numbers (because we can add in any order).

Example \(\PageIndex{15}\)

Simplify \(− 3 − 7 + 5 + 7 + 13 − 6 − (−9)\).

Solution

\(\begin{align*} & − 3 − 7 + 5 + 7 + 13 − 6 − (−9) \\ = & −3 + (−7) + 5 + 7 + 13 + (−6) + 9 \\ = & −3 + (−7) + (−6) + 5 + 7 + 13 + 9 \\ = &-16 +34 \\=& 18 \end{align*}\)

Remark \(\PageIndex{16}\)

Warning: The symbol "-" is used in two different ways. When it is between two expressions, it means subtract (e.g., \(3-4\) ). Otherwise, it means 'opposite' or 'negative' (e.g., \(-3+4\) ). So in the expression \(-4-(-3)\), the first and last "-" means opposite and the one in the middle one means subtract. The importance of understanding this can not be overestimated.

Try It \(\PageIndex{17}\)

Simplify:

a. \(-3-9\)

b. \(9-(-6)\)

c. \(4-9+8-(-3)+1\)

d. \(-2-(-4)+8+(-4)-(-7)\)

Answer

a. \(-12\)

b. \(15\)

c. \(1\)

d. \(13\)

Multiplication and Division of Positive Numbers

Multiplication of positive integers is adding in the sense that \(3 \times 4=4+4+4\).  

We can also view this multiplication as counting boxes in the image below, or calculating the area of the image below if each box is one square foot, say:

To multiply larger numbers, it is better to use the usual scheme of multiplication. For example:

Example \(\PageIndex{18}\)

Multiply 152 by 34.

Solution

We will for convenience sake put the smaller number on the bottom (though it is not necessary). We have

\(\begin{array}{lllll}
& & 1 & 5 & 2 \\
& \times & & 3 & 4 \\
\hline & & 6 & 0 & 8 \\
+ & 4 & 5 & 6 & 0 \\
\hline & 5 & 1 & 6 & 8
\end{array}\)

And division is the opposite of multiplication in the sense that to compute \(45 \div 9\) is to find a number so that when we multiply by 9 we get 45. We run through our multiplication tables (which are hopefully in our head) to discover that 5 does the trick: \(5 \times 9=45\) so that \(45 \div 9=5 .\) We will discuss division from a different point of view when we discuss fractions.

To divide larger numbers, we can use long division. For example,

Example \(\PageIndex{19}\)

Divide 3571 by 11.

Solution

Try It \(\PageIndex{20}\)

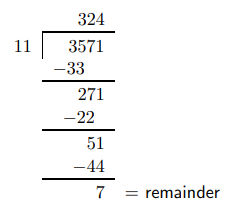
a. Mulitply \(36\times102\).

b. Divide \(2345\div 14\).

Answer

a. \(3672\)

b. \(167\) with a remainder of \(7\)

Multiplication involving negative numbers

Multiplication is a little tricky to understand without the notion of distribution (discussed later). We will begin with noting again what it means to multiply a number by a positive number.  As with multiplication of positive integers,  multiplication by a positive integer is really a short hand for a more lengthy addition problem: 

\[4 \cdot(-7)=(-7)+(-7)+(-7)+(-7)=-28\nonumber\]

Note that since \(4 \cdot 7=28,4 \cdot(-7)=-(4 \cdot 7) .\) We can multiply positive numbers in any order: \(4 \cdot 7=7 \cdot 4\). The same is true of positive and negative numbers:

\[(-7) \cdot 4=4 \cdot(-7)=-(4 \cdot 7)=-28\nonumber\]

Example \(\PageIndex{21}\)

Multitply:

a. \(5 \cdot(-12)\)

b. \((-3) \cdot(-2)\) 

Solution

a. \(5 \cdot(-12)=-(5 \cdot 12)=-60\)

b. \((-3) \cdot(-2)=-(3 \cdot(-2))=-(-(3 \cdot 2))=6\) 

Note that the magnitude of the product of two numbers is the product of their magnitudes. The sign is positive if the signs are the same and negative if they are different. 

Notation

Two quantities right next to each other, with no symbol between them (except for parentheses around either or both numbers), has an implicit multiplication. For example, \(3(2)=3 \times 2\).

Example \(\PageIndex{22}\)

Multiply:

a. \((-5)(-8)\)

b. \((-6) \cdot 7\)

c. \(4 \cdot 12\)

d. \((-3)(-6) \cdot 4(-3)\)

e. \((-3)(-5) \cdot 4(-2)\) 

Solution

a. \((-5)(-8)=40\)

b. \((-6) \cdot 7=-42\)

c. \(4 \cdot 12=48\)

d. \((-3)(-6) \cdot 4(-3)=18 \cdot 4(-3)=72(-3)=-216(\text { multiplying from left to right })\)

e. \((-3)(-5) \cdot 4(-2)=(-3) \cdot 4 \cdot(-5)(-2)=-12 \cdot 10=-120(\) since we can multiply in any order it is convenient to see that \(-5 \cdot-2=10 .\) )

Try It \(\PageIndex{23}\)

Multiply:

a. \((-3)(4)\)

b. \((-2) \cdot (-3)\)

c. \(5 \cdot 11\)

d. \((2)(-3) \cdot 4(-5)\)

e. \((25)(-3) \cdot (-6)(-4)\) 

Answer

a. \(-12\)

b. \(6\)

c. \(55\)

d. \(120\)

e. \(1800\)

Division involving negative numbers

What does it mean to divide?  \(A\div B\) is the number you need to multiply \(B\) by to get \(A\).  Some will say '\(B\) goes into \(A\)' \(A\div B\) times.  For example, \(6\div (-3)\) is \(-2\) because \((-2)(-3)=6.\). 

Example \(\PageIndex{24}\)

Divide:

a. \((-42) \div 7\)

b. \(81 \div(-9)\)

c. \((-35) \div(-7)\)

d. \(14 \div 2\)

e. \(0 \div 5\)

f. \(-10 \div 0\)

Solution

a. \((-42) \div 7=-6\)

b. \(81 \div(-9)=-9\)

c. \((-35) \div(-7)=5\)

d. \(14 \div 2=7\)

e. \(0 \div 5=0\). Note When dividing 0 by any number, the answer is always 0.

f. \(-10 \div 0=\) undefined.

Note \(\PageIndex{25}\)

Any number divided by 0 is undefined!

Multiplying and Dividing Integers

Consider two numbers at a time.

1. If the signs of the two numbers are the same, then the sign of the answer is positive.
2. If the signs of the two numbers are different, then the sign of the answer is negative.

Exeample \(\PageIndex{26}\)

Divide:

a. \((-15) \div 0\)

b. \(-15 \div(-3)\)

c. \((20) \div(-4)\)

d. \(0 \div 2\)

e. \((-72) \div 3\)

f. \(10 \div 5\)

Answer

a. Undefined

b. \(5\)

c. \(-5\)

d. \(0\)

e. \(-24\)

f. \(2\)

Writing Exercises \(\PageIndex{27}\)

1. Give an application of adding two positive numbers.  Give an application of adding two negative numbers.
2. Give an application of multiplying two positive numbers.
3. Give an example of multiplying a positive number and a negative number.
4. Explain how addition and subtraction are related.  Include an example.
5. Explain how multiplication and division are related.  Include an example.

Exit Problem

Simplify:

1. \((-7)+5-(-8)\)
2. \((-7)(5)(-8)\)
3. \(\dfrac{87}{4}\)

Key Concepts

• Adding integers

• Subtracting integers

• Multiplying integers

• Dividing integers