1.3.2: Simplifying, Multiplying and Dividing Rational Expressions
- Page ID
- 93952
By the end of this section, you will be able to:
- Determine the values for which a rational expression is undefined
- Simplify rational expressions
- Multiply rational expressions
- Divide rational expressions
Before you get started, take this readiness quiz.
- Simplify \(\dfrac{90y}{15y^2}\).
- Multiply \(\dfrac{14}{15}·\dfrac{6}{35}\).
- Divide \(\dfrac{12}{10}÷\dfrac{8}{25}\).
Above are examples of some properties of fractions and their operations. Recall that these fractions where the numerators and denominators are integers are called rational numbers. In this chapter, we will work with fractions whose numerators and denominators are polynomials. We call this kind of expression a rational expression.
A rational expression is an expression of the form \(\dfrac{p}{q}\), where \(p\) and \(q\) are polynomials and \(q\neq 0\).
Here are some examples of rational expressions:
\[−\dfrac{24}{56} \qquad \dfrac{5x}{12y} \qquad \dfrac{4x+1}{x^2−9} \qquad \dfrac{4x^2+3x−1}{2x−8}\nonumber\]
Notice that the first rational expression listed above, \(−\dfrac{24}{56}\), is just a fraction. Since a constant is a polynomial with degree zero, the ratio of two constants is a rational expression, provided the denominator is not zero.
We will do the same operations with rational expressions that we did with fractions. We will simplify, add, subtract, multiply, divide and use them in applications.
Simplify Rational Expressions
Here we recall for example, \(\dfrac12=\dfrac{6}{12}\), which can be understood by imagining dividing a pizza into 2 pieces and eating 1, and imagining dividing the pizza up into 12 pieces and eating 6 of them! In general, \(\dfrac{a}{b}=\dfrac{ca}{cb}\) when \(c\) and \(b\) are not zero. The process of replacing \(\dfrac{ca}{cb}\) by the equivalent expression \(\dfrac{a}{b}\) is called reducing the fraction. It is commonly also called 'canceling' the common factor \(c\).
A fraction is considered simplified if there are no common factors, other than \(1\) and \(-1\), in its numerator and denominator. Similarly, a simplified rational expression has no common factors, other than \(1\) and \(-1\), in its numerator and denominator.
A rational expression is considered simplified if there are no common factors other than \(1\) and \(-1\) in its numerator and denominator. There should be no more "\(-\)"s than necessary.
For example,
\[ \begin{array} {l} \dfrac{x+2}{x+3} \text{ is simplified because there are no common factors of } x+2 \text{ and }x+3. \\ \dfrac{2x}{3x} \text{ is not simplified because \(x\) is a common factor of }2x\text{ and }3x. \\ \end{array} \nonumber\]
We use the Equivalent Fractions Property to simplify numerical fractions. We restate it here as we will also use it to simplify rational expressions.
If \(a\), \(b\), and \(c\) are numbers where \(b\neq 0,c\neq 0,\)
\[\text {then } \dfrac{a}{b}=\dfrac{a\cdot c}{b\cdot c} \text{ and } \dfrac{a\cdot c}{b\cdot c}=\dfrac{a}{b}\nonumber\]
Notice that in the Equivalent Fractions Property, the values that would make the denominators zero are specifically disallowed. We see \(b\neq 0\), \(c\neq 0\) clearly stated.
To simplify rational expressions, we first write the numerator and denominator in factored form. Then we remove the common factors using the Equivalent Fractions Property.
Be very careful as you remove common factors. Factors are multiplied to make a product. You can remove a factor from a product. You cannot remove a term from a sum.

Removing the \(x\)'s from \(\dfrac{x+5}{x}\) would be like cancelling the \(2\)’s in the fraction \(\dfrac{2+5}{2}!\)
Simplifying Rational Expressions: Monomials over Monomials
Now we will look at an exponent property for division. As before, we’ll try to discover a property by looking at some examples.
| Consider | \(\quad\dfrac{x^5}{x^2}\) | and | \(\quad\dfrac{x^2}{x^3}\) |
|---|---|---|---|
| What do they mean? | \(=\dfrac{x\cdot x\cdot x\cdot x\cdot x}{x\cdot x}\) | \(=\dfrac{x\cdot x}{x\cdot x\cdot x}\) | |
| Use the Equivalent Fractions Property. | \(=\dfrac{\cancel{x}\cdot\cancel{x}\cdot x\cdot x\cdot x}{\cancel{x}\cdot \cancel{x}}\) | \(=\dfrac{\cancel{x}\cdot \cancel{x}\cdot 1}{\cancel{x}\cdot \cancel{x}\cdot x}\) | |
| Simplify. | \(=x^3\) |
\(=\dfrac{1}{x}\) (This is not a polynomial!) |
|
| Note. |
\(\quad\dfrac{x^5}{x^2}=\dfrac{x^2x^3}{x^2}=x^3\) Reducing the fraction. |
\(\quad\dfrac{x^2}{x^3}=\dfrac{x^2}{x^2x}=\dfrac{1}{x}\) Reducing the fraction. |
Note that the result when you divide monomials is not necessarily a polynomial!
Simplify \(\dfrac{54a^2b^3}{−6ab^5}\).
Solution
When we divide monomials with more than one variable, we write one fraction for each variable.
| \(\quad \dfrac{54a^2b^3}{−6ab^5}\) | |
|---|---|
| Rewrite as a fraction. | \(=\dfrac{54a^2b^3}{−6ab^5}\) |
| Use fraction multiplication. | \(=\dfrac{54}{−6}\cdot \dfrac{a^2}{a}\cdot\dfrac{b^3}{b^5}\) |
| Simplify and use the Quotient Property. | \(=−9a\cdot\dfrac{1}{b^2}\) |
| Multiply. | \(=−\dfrac{9a}{b^2}\) |
Simplify \(-\dfrac{72a^7b^3}{(8a^{12}b^4}\).
- Answer
-
\(−\dfrac{9}{a^5b}\)
Simplify \(−\dfrac{63c^8d^3}{7c^{12}d^2}\).
- Answer
-
\(\dfrac{−9d}{c^4}\)
Once you become familiar with the process and have practiced it step by step several times, you may be able to simplify a fraction in one step.
Simplify \(\dfrac{14x^7y^{12}}{21x^{11}y^6}\).
Solution
Be very careful to simplify \(\dfrac{14}{21}\) by dividing out a common factor, and to simplify the variables by subtracting their exponents.
| \(\quad\dfrac{14x^7y^{12}}{21x^{11}y^6}\) | |
| Simplify and use the Quotient Property. | \(=\dfrac{2y^6}{3x^4}\) |
Simplify \(\dfrac{28x^5y^{14}}{49x^9y^{12}}\).
- Answer
-
\(\dfrac{4y^2}{7x^4}\)
Simplify \(\dfrac{30m^5n^{11}}{48m^{10}n^{14}}\).
- Answer
-
\(\dfrac{5}{8m^5n^3}\)
Simplifying Rational Expressions: Polynomials over Monomials
Now that we know how to divide a monomial by a monomial, the next procedure is to divide a polynomial of two or more terms by a monomial. The method we’ll use to divide a polynomial by a monomial is based on the properties of fraction addition. It is clear that \(\dfrac{2+3}{7}=\dfrac{2}{7}+\dfrac{3}{7}\) because the left side is \(5\) sevenths and the right side is \(2\) sevenths plus \(3\) sevenths. You may also see this as \(\dfrac17(2+3)=\dfrac17 2+\dfrac17 3=\dfrac27+\dfrac37.\) So in other words, we distribute division over addition (and subtraction) just as we did multiplication. Since variables are place-holders for numbers, it will be the same if instead of numbers we have variables.
For example, the sum \(\dfrac{y}{5}+\dfrac{2}{5}\) simplifies to \(\dfrac{y+2}{5}\). Now we will do this in reverse to split a single fraction into separate fractions. For example, \(\dfrac{y+2}{5}\) can be written \(\dfrac{y}{5}+\dfrac{2}{5}\).
This is the “reverse” of fraction addition and it states that if a, b, and c are numbers where \(c\neq 0\), then \(\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\). We will use this to divide polynomials by monomials.
To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.
Simplify \(\dfrac{18x^3y−36xy^2}{−3xy}\).
Solution
| \(\quad \dfrac{18x^3y−36xy^2}{−3xy}\) | |
| Rewrite as a fraction. | \(=\dfrac{18x^3y−36xy^2}{−3xy}\) |
| Divide each term by the divisor. Be careful with the signs! | \(=\dfrac{18x^3y}{−3xy}−\dfrac{36xy^2}{−3xy}\) |
| Simplify. | \(=−6x^2+12y\) |
Simplify \(\dfrac{32a^2b−16ab^2}{−8ab}\).
- Answer
-
\(−4a+2b\)
Simplify \(\dfrac{−48a^8b^4−36a^6b^5}{−6a^3b^3}\).
- Answer
-
\(8a^5b+6a^3b^2\)
Simplifying Rational Expressions: Polynomials over Polynomials
Simplify \(\dfrac{x^2+5x+6}{x^2+8x+12}.\)
- Solution
-
\(\quad \dfrac{x^2+5x+6}{x^2+8x+12}\) Factor the numerator and denominator completely. \(= \dfrac{(x+2)(x+3)}{(x+2)(x+6)}\) Simplify by dividing out common factors. \(= \dfrac{\cancel{(x+2)}(x+3)}{\cancel{(x+2)}(x+6)}\)
\(=\dfrac{x+3}{x+6}\)
for the values of \(x\) where \
\(\quad \dfrac{x^2+5x+6}{x^2+8x+12}= \dfrac{(x+2)(x+3)}{(x+2)(x+6)}\) and \(\dfrac{x+3}{x+6}\)
are both defined.
Simplify \(\dfrac{x^2−x−2}{x^2−3x+2}\).
- Answer
-
\(\dfrac{x+1}{x−1}\) for values of \(x\) where \(\dfrac{x^2−x−2}{x^2−3x+2}\) is defined.
Simplify \(\dfrac{x^2−3x−10}{x^2+x−2}\).
- Answer
-
\(\dfrac{x−5}{x−1}\) where \(\dfrac{x^2−3x−10}{x^2+x−2}\) is defined.
Note that in the example it is noted that the equality is valid only where \(\quad \dfrac{x^2+5x+6}{x^2+8x+12}= \dfrac{(x+2)(x+3)}{(x+2)(x+6)}\) and \(\dfrac{x+3}{x+6}\) are defined. The latter is defined everywhere because one can always ad and multiply numbers. The problem is what when \(\quad \dfrac{x^2+5x+6}{x^2+8x+12}= \dfrac{(x+2)(x+3)}{(x+2)(x+6)}\) is not defined. For example, if \(x=-2\) the denominator is 0 (check by evaluating) and so the quotient is undefined whereas \(\dfrac{x+3}{x+6}=\dfrac{-2+3}{-2+6}=\dfrac{1}{4}\) which is defined so that for \(x=-2\), \(\dfrac{x^2+5x+6}{x^2+8x+12}\not=\dfrac{x+3}{x+6}\). Maybe you can spot another value that doesn't give equality. If the two expressions are defined then they are equal, which is most values of \(x\). In the context of an application, it will be necessary to go back and make sure the equality holds for the value of interest. We will see this in action in the next unit.
We now summarize the steps you should follow to simplify rational expressions.
- Factor the numerator and denominator completely.
- Simplify by noting common factors.
Usually, we leave the simplified rational expression in factored form. This way, it is easy to check that we have removed all the common factors.
We’ll use the methods we have learned to factor the polynomials in the numerators and denominators in the following examples.
Every time we write a rational expression, we should make a statement disallowing values that would make a denominator zero. However, to let us focus on the work at hand, we will omit writing it in the examples.
Simplify \(\dfrac{3a^2−12ab+12b^2}{6a^2−24b^2}\).
- Solution
-
\(\quad \dfrac{3a^2−12ab+12b^2}{6a^2−24b^2}\) Factor the numerator and denominator, first factoring out the GCF. \(= \dfrac{3(a^2−4ab+4b^2)}{6(a^2−4b^2)}\)
\(=\dfrac{3(a−2b)(a−2b)}{6(a+2b)(a−2b)}\)
Remove the common factors of \(a−2b\) and \(3\). \(=\dfrac{\cancel{3}(a−2b)\cancel{(a−2b)}}{\cancel{3}\cdot 2(a+2b)\cancel{(a−2b)}}\)
\(=\dfrac{a−2b}{2(a+2b)}\)
Conclude. \(\quad \dfrac{3a^2−12ab+12b^2}{6a^2−24b^2}==\dfrac{a−2b}{2(a+2b)}\)
where both sides are defined.
Simplify \(\dfrac{2x^2−12xy+18y^2}{3x^2−27y^2}\).
- Answer
-
\(\dfrac{2(x−3y)}{3(x+3y)}\)
Simplify \(\dfrac{5x^2−30xy+25y^2}{2x^2−50y^2}\).
- Answer
-
\(\dfrac{5(x−y)}{2(x+5y)}\)
Now we will see how to simplify a rational expression whose numerator and denominator have opposite factors. We previously introduced opposite notation: the opposite of \(a\) is \(−a\) and \(−a=−1\cdot a\).
The numerical fraction, say \(\dfrac{7}{−7}\) simplifies to \(−1\). We also recognize that the numerator and denominator are opposites.
The fraction \(\dfrac{a}{−a}\), whose numerator and denominator are opposites also simplifies to \(−1\).
\[\begin{array} {ll} \text{Let’s look at the expression }b−a. &b−a \\ \text{Rewrite.} &−a+b \\ \text{Factor out }–1. &−1(a−b) \nonumber\end{array} \]
This tells us that \(b−a\) is the opposite of \(a−b\).
In general, we could write the opposite of \(a−b\) as \(b−a\). So the rational expression \(\dfrac{a−b}{b−a}\) simplifies to \(−1\).
The opposite of \(a−b\) is \(b−a\).
\[\dfrac{a−b}{b−a}=−1 \quad a\neq b\nonumber\]
An expression and its opposite divide to \(−1\).
We will use this property to simplify rational expressions that contain opposites in their numerators and denominators. Be careful not to treat \(a+b\) and \(b+a\) as opposites. Recall that in addition, order doesn’t matter so \(a+b=b+a\). So if \(a\neq −b\), then \(\dfrac{a+b}{b+a}=1\).
Simplify \(\dfrac{x^2−4x−32}{64−x^2}.\)
- Solution
-
\(\quad \dfrac{x^2−4x−32}{64−x^2}\) Factor the numerator and the denominator. \(=\dfrac{(x-8)(x+4)}{(8-x)(8+x)}\)
Recognize the factors that are opposites. \(=({\color{red}{-1}})\dfrac{\cancel{(x-8)}(x+4)}{\cancel{(8-x)}(8+x)}\)
Simplify. \(=-\dfrac{x+4}{x+8}\)
Conclude. \(\dfrac{x^2−4x−32}{64−x^2}=-\dfrac{x+4}{x+8}\)
where both sides are defined.
Simplify \(\dfrac{x^2−4x−52}{5−x^2}\)
- Answer
-
\(−\dfrac{x+1}{x+5}\)
Simplify \(\dfrac{x^2+x−2}{1−x^2}\).
- Answer
-
\(−\dfrac{x+2}{x+1}\)
Multiplying Rational Expressions
To multiply rational expressions, we do just what we did with numerical fractions. We multiply the numerators and multiply the denominators. Then, if there are any common factors, we remove them to simplify the result.
If \(p\), \(q\), \(r\), and \(s\) are polynomials where \(q\neq 0\), \(s\neq 0\), then
\[\dfrac{p}{q}\cdot \dfrac{r}{s}=\dfrac{pr}{qs}.\nonumber\]
To multiply rational expressions, multiply the numerators and multiply the denominators.
Remember, throughout this chapter, we will assume that all numerical values that would make the denominator be zero are excluded. We will not write the restrictions for each rational expression, but keep in mind that the denominator can never be zero. So in this next example, \(x\neq 0\), \(x\neq 3\), and \(x\neq 4.\)
Simplify \(\dfrac{2x}{x^2−7x+12}\cdot \dfrac{x^2−9}{6x^2}\).
- Solution
-
Step 1. Factor each numerator and denominator completely. Factor \(x^2-9\) and \(x^2-7x+12\). \(\dfrac{2x}{x^2-7x+12}\cdot\dfrac{x^2-9}{6x^2}\)
\(=\dfrac{2x}{(x-3)(x-4)}\cdot\dfrac{(x-3)(x+3)}{6x^2}\)
Step 2. Multiply the numerators and denominators. Multiply the numerators and denominators. It is helpful to write the monomials first. \(=\dfrac{2x(x-3)(x+3)}{6x^2(x-3)(x-4)}\) Step 3. Reduce the fraction. Recognize factors common to the numerator and denominator and reduce the fraction. "Divide out" the common factors (divide numerator and denominator by those common factors). Leave the result in factored form. \(\dfrac{\cancel{2}\cancel{x}\cancel{(x-3)}(x+3)}{\cancel{2}\cdot 3\cdot \cancel{x}\cdot x\cancel{(x-3)}(x-4)}\)
\(=\dfrac{x+3}{3x(x-4)}\)
Conclude. \(\dfrac{2x}{x^2−7x+12}\cdot \dfrac{x^2−9}{6x^2}=\dfrac{x+3}{3x(x-4)}\)
where both sides are defined.
Note that we will stop writing the qualification that the expressions of interest are defined. It will be tacitly understood for the rest of this chapter.
Simplify \(\dfrac{5x}{x^2+5x+6}\cdot \dfrac{x^2−4}{10x}\).
- Answer
-
\(\dfrac{x−2}{2(x+3)}\)
Simplify \(\dfrac{9x^2}{x^2+11x+30}]\cdot\dfrac{x^2−36}{3x^2}\).
- Answer
-
\(\dfrac{3(x−6)}{x+5}\)
- Factor each numerator and denominator completely.
- Multiply the numerators and denominators.
- Simplify by dividing out the common factors.
Multiply \(\dfrac{3a^2−8a−3}{a^2−25}·\dfrac{a^2+10a+25}{3a^2−14a−5}\).
- Solution
-
\(\begin{array} {ll} &\dfrac{3a^2−8a−3}{a^2−25}·\dfrac{a^2+10a+25}{3a^2−14a−5} \\ & \\ \begin{array} {ll} \text{Factor the numerators and denominators} \\ \text{and then multiply.} \end{array} &\dfrac{(3a+1)(a−3)(a+5)(a+5)}{(a−5)(a+5)(3a+1)(a−5)} \\ & \\ \begin{array} {l} \text{Simplify by dividing out} \\ \text{common factors.} \end{array} &\dfrac{\cancel{(3a+1)}(a−3)\cancel{(a+5)}(a+5)}{(a−5)\cancel{(a+5)}\cancel{(3a+1)}(a−5)} \\ & \\ \text{Simplify.} &\dfrac{(a−3)(a+5)}{(a−5)(a−5)} \\ & \\ \text{Rewrite }(a−5)(a−5)\text{ using an exponent.} &\dfrac{(a−3)(a+5)}{(a−5)^2} \end{array}\),
where \(\dfrac{3a^2−8a−3}{a^2−25}·\dfrac{a^2+10a+25}{3a^2−14a−5}\) is defined (then \(\dfrac{(a−3)(a+5)}{(a−5)^2}\) is also defined).
Simplify \(\dfrac{2x^2+5x−12}{x^2−16}·\dfrac{x^2−8x+16}{2x^2−13x+15}\).
- Answer
-
\(\dfrac{x−4}{x−5}\)
Simplify \(\dfrac{4b^2+7b−2}{1−b^2}·\dfrac{b^2−2b+1}{4b^2+15b−4}\).
- Answer
-
\(−\dfrac{(b+2)(b−1)}{(1+b)(b+4)}\)
Dividing Rational Expressions
Just like we did for numerical fractions, to divide rational expressions, we multiply the first fraction by the reciprocal of the second.
If \(p\), \(q\), \(r\), and \(s\) are polynomials where \(q\neq 0\), \(r\neq 0\), \(s\neq 0\), then
\[\dfrac{p}{q}\div\dfrac{r}{s}=\dfrac{p}{q}\cdot \dfrac{s}{r}.\nonumber\]
To divide rational expressions, multiply the first fraction by the reciprocal of the second.
Once we rewrite the division as multiplication of the first expression by the reciprocal of the second, we then factor everything and look for common factors.
Divide \(\dfrac{p^3+q^3}{2p^2+2pq+2q^2}÷\dfrac{p^2−q^2}{6}\). Use the fact that \(p^3+q^3=(p+q)(p^2-pq+q^2)\).
- Solution
-




So, \(\dfrac{p^3+q^3}{2p^2+2pq+2q^2}÷\dfrac{p^2−q^2}{6}=\dfrac
Simplify \(\dfrac{x^3−8}{3x^2−6x+12}\div\dfrac{x^2-4}{6}\). Use the fact that \(x^3−8=(x-2)(x^2+2x+4)\).
- Answer
-
\(\dfrac{2(x^2+2x+4)}{(x+2)(x^2−2x+4)}\)
Simplify \(\dfrac{2z^2}{z^2−1}\div\dfrac{z^3−z^2+z}{z^3+1}\). Use \(z^3+1=(z+1)(z^2-z+1)\) and don't forget to factor out greatest common factors.
- Answer
-
\(\dfrac{2z}{z−1}\)
- Rewrite the division as the product of the first rational expression and the reciprocal of the second.
- Factor the numerators and denominators completely.
- Multiply the numerators and denominators together.
- Simplify by dividing out common factors.
A complex fraction is a fraction that contains a fraction in the numerator, the denominator or both. Recall that a fraction bar means division. A complex fraction is another way of writing division of two fractions.
Divide \(\dfrac{\dfrac{6x^2−7x+2}{4x−8}}{\dfrac{2x^2−7x+3}{x^2−5x+6}}\).
- Solution
-
\(\begin{array} {ll} &\dfrac{\dfrac{6x^2−7x+2}{4x−8}}{\dfrac{2x^2−7x+3}{x^2−5x+6}} \\ & \\ \text{Rewrite with a division sign.} &\dfrac{6x^2−7x+2}{4x−8}÷\dfrac{2x^2−7x+3}{x^2−5x+6} \\ & \\ \begin{array} {l} \text{Rewrite as product of first times reciprocal} \\ \text{of second.} \end{array} &\dfrac{6x^2−7x+2}{4x−8}·\dfrac{x^2−5x+6}{2x^2−7x+3} \\ & \\ \begin{array} {l} \text{Factor the numerators and the} \\ \text{denominators, and then multiply.} \end{array} &\dfrac{(2x−1)(3x−2)(x−2)(x−3)}{4(x−2)(2x−1)(x−3)} \\ & \\ \text{Simplify by dividing out common factors.} &\dfrac{\cancel{(2x−1)}(3x−2)\cancel{(x−2)}\cancel{(x−3)}}{4\cancel{(x−2)}\cancel{(2x−1)}\cancel{(x−3)}} \\ \text{Simplify.} &\dfrac{3x−2}{4} \end{array}\)
Simplify \(\dfrac{\dfrac{3x^2+7x+2}{4x+24}}{\dfrac{3x^2−14x−5}{x^2+x−30}}\).
- Answer
-
\(\dfrac{x+2}{4}\)
Simplify \(\dfrac{\dfrac{y^2−36}{2y^2+11y−6}}{\dfrac{2y^2−2y−60}{8y−4}}\).
- Answer
-
\(\dfrac{2}{y+5}\)
If we have more than two rational expressions to work with, we still follow the same procedure. The first step will be to rewrite any division as multiplication by the reciprocal. Then, we factor and multiply.
Perform the indicated operations: \(\dfrac{3x−6}{4x−4}·\dfrac{x^2+2x−3}{x^2−3x−10}÷\dfrac{2x+12}{8x+16}\).
- Solution
-
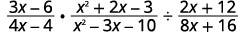
Rewrite the division as multiplication
by the reciprocal.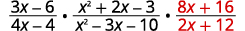
Factor the numerators and the denominators. 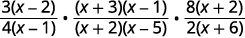
Multiply the fractions. Bringing the constants to
the front will help when removing common factors.Simplify by dividing out common factors. 
Simplify. 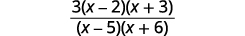
Perform the indicated operations: \(\dfrac{4m+4}{3m−15}·\dfrac{m^2−3m−10}{m^2−4m−32}÷\dfrac{12m−36}{6m−48}\).
- Answer
-
\(\dfrac{2(m+1)(m+2)}{3(m+4)(m−3)}\)
Perform the indicated operations: \(\dfrac{2n^2+10n}{n−1}÷\dfrac{n^2+10n+24}{n^2+8n−9}·\dfrac{n+4}{8n^2+12n}\).
- Answer
-
\(\dfrac{(n+5)(n+9)}{2(n+6)(2n+3)}\)
- What is a rational expression?
- What is the first goal when aiming at simplifying rational expressions? Why is this the first goal?
- Give an example of dividing a rational expression where the reduced result is a quotient of linear expressions.
- a. Multiply \(\dfrac{7}{4}·\dfrac{9}{10}\) and explain all your steps.
b. Multiply \(\dfrac{n}{n−3}·\dfrac{9}{n+3}\) and explain all your steps.
c. Evaluate your answer to part b. when \(n=7\). Did you get the same answer you got in part a.? Why or why not - a. Divide \(\dfrac{24}{5}÷6\) and explain all your steps.
b. Divide \(\dfrac{x^2−1}{x}÷(x+1)\) and explain all your steps.
c. Evaluate your answer to part b. when \(x=5\). Did you get the same answer you got in part a.? Why or why not?
Simplify:
a. \(\dfrac{5p^2}{p^2−5p−36}\cdot\dfrac{p^2−16}{10p}\)
b. \(\dfrac{2y^2−10y}{y^2}+\dfrac{10y+2}{5}\cdot\dfrac{y+5}{6y}\)
Key Concepts
- Determine the values for which a rational expression is undefined.
- Set the denominator equal to zero.
- Solve the equation.
- Equivalent Fractions Property
If \(a\), \(b\), and \(c\) are numbers where \(b\neq 0\), \(c\neq 0\), then
\(\quad\dfrac{a}{b}=\dfrac{a·c}{b·c}\) and \(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\) - How to simplify a rational expression.
- Factor the numerator and denominator completely.
- Simplify by dividing out common factors. (The resulting equality holds for values of the variable where the initial expression is defined.)
- Opposites in a Rational Expression
The opposite of \(a−b\) is \(b−a\).
\(\quad\dfrac{a−b}{b−a}=−1 \qquad a\neq b\)
An expression and its opposite divide to \(−1\). - Multiplication of Rational Expressions
If \(p\), \(q\), \(r\), and \(s\) are polynomials where \(q\neq 0\), \(s\neq 0\), then
\(\quad\dfrac{p}{q}·\dfrac{r}{s}=\dfrac{pr}{qs}\) - How to multiply rational expressions.
- Factor each numerator and denominator completely.
- Multiply the numerators and denominators.
- Simplify by dividing out common factors.
- Division of Rational Expressions
If \(p\), \(q\), \(r\), and \(s\) are polynomials where \(q\neq 0\), \(r\neq 0\), \(s\neq 0\), then
\(\quad\dfrac{p}{q}÷\dfrac{r}{s}=\dfrac{p}{q}·\dfrac{s}{r}\) - How to divide rational expressions.
- Rewrite the division as the product of the first rational expression and the reciprocal of the second.
- Factor the numerators and denominators completely.
- Multiply the numerators and denominators together.
- Simplify by dividing out common factors.


