4.3.2: Evaluating Logarithmic Expressions
- Page ID
- 93996
By the end of this section, you will be able to:
- Convert between exponential and logarithmic form
- Understand what a logarithm is.
- Estimate the value of logarithms and evaluate certain logarithms exactly without a calculator.
- Evaluate logarithmic expressions
- Graph basic logarithmic equations
- Solve logarithmic equations
- Use logarithmic models in applications
Before you get started, take this readiness quiz.
1. Simplify \(\left(\sqrt{81}\right)^{2}\).
2. Evaluate \(2^3\).
3. Evaluate \(3^{−2}\).
4. Write \(\sqrt[3]{7} \) using exponents.
It works well to ‘undo’ an operation with another operation. Subtracting ‘undoes’ addition, multiplication ‘undoes’ division, taking the square root ‘undoes’ squaring.
|
Subtraction 'undoes' addition: |
\(x+3-3=x\) \(x-3+3=x\) |
|---|---|
| Division 'undoes' multiplication: |
\(\dfrac{1}{3}\cdot(3x)=x\) or \(\dfrac{3x}{3}=x\) \(3\cdot\left(\dfrac{x}{3}\right)=x\) |
| square root 'undoes' squaring (same button on calculator!) |
\((\sqrt{x})^2=x\) \(\sqrt{x^2}=x\) for \(x\geq 0\). |
|
What undoes the exponential \(e^x\)? What about \(10^x\)? and more generally, \(a^x\)? |
The calculator likely carries the answer or at least part of it! |
In the previous section we learned about exponential expressions and how to evaluate them. In this section we will learn about a related type of expression, namely, the logarithmic expression.
Suppose we want to solve a simple exponential equation \(2^x=16\). Because we know how to evaluate it, we can use trial and error with a calculator to find an approximation to the value of \(x\). What we are looking for is the value of the exponent we need to raise the base 2 to to arrive at 16. This exponent (which depends on the base and the result) is called \(\log_2(16)\).
In general,
Assume \(b>0\). Then \(\log_b(a)\) ('the logarithm with base \(b\) of a') is the exponent we need on the base \(b\) to arrive at a value of \(a\),
or in other words, \(\log_b(a)\) is the solution to
\(b^x=a\).
You might wonder why we assume the base of the logarithm should be positive. What are the issues when this isn't the case?
Evaluate \(\log_5 25\).
Solution
We are looking here for the exponent we need to raise \(5\) to in order to arrive at 25. But we know \(5^2=25\). It follows that
\(\log_5 25=2\).
Evaluate
- \(\log_3 27\)
- \(\log_{10}\left(\dfrac{1}{100}\right)\)
- \(\log_{16}4\)
- Answer
-
- 3
- -2
- \(\dfrac12\)
Now, we will also note that
\[\log_b b^c =c\]
since we need to raise the base \(b\) to the exponent \(c\) in order to arrive at \(b^c\).
Evaluate \(\log_5 (25\sqrt{5})\).
Solution
We are looking here for the exponent we need to raise \(5\) to in order to arrive at \(25\sqrt{5}\). But we know \(25\sqrt{5}=5^2\cdot 5^\frac12=5^{2+\frac12}=5^\frac52\). It follows that
\(\log_5 (25\sqrt{5})=\dfrac52\)
Evaluate:
- \(\log_3 27\sqrt[4]3\)
- \(\log_{10}\left(\dfrac{\sqrt[3]{100}}{100}\right)\)
- \(\log_{16}\left(\dfrac{4}{\sqrt[3]{16}}\right)\)
- Answer
-
- \(\dfrac{13}{3}\)
- \(-\dfrac{4}{3}\)
- \(\dfrac16\)
Note that just solving equations \(x^2=15\) involves the use of the square root, solving an equation \(2^x=15\) involves the logarithm. Most calculators reflect this analogy by the placement of the buttons. There are typically two easily accessible logarithm buttons: 'log' which is shorthand for \(\log_{10}\) and 'ln' which is shorthand for \(\log_e\). Others logarithms will require additional understanding or a fancy calculator to approximate. Here we will give some examples using only the trial and error method for evaluation.
Approximate \(\log_5 7\).
Solution
This is equivalent to finding an approximate solution to \(5^x=7\).
We note that \(5^1=5\) and \(5^2=25\), so the exponent we seek is between these to exponents since \(5<7<25\). In fact \(7\) is closer to \(5\) so we expect that our sought-for exponent is closer to 1. We use our calculator to evaluate \(5^{1.1}\), \(5^{1.2}\) and \(5^{1.3}\). we find that our desired exponent is between \(1.2\) and \(1.3\) and probably closer to 1.2. Evaluating \(5^{1.21}\approx 7.01\) is enough to know the exponent we seek is between \(1.2\) and \(1.21\), probably closer to the latter. Evaluating \(5^{1.209}\approx 6.9992\) is enough to conclude that our exponent is between \(1.209\) and \(1.21\) and, in particular, rounded to the nearest hundredth,
\(\log_5 (7)\approx 1.21.\)
Approximate \(\log_{\frac{1}{2}}(7)\) to the nearest hundredth
- Answer
-
-2.81
The solution to the equation \(x=a^y\) is written
\(\log_{a}x\) and is called the logarithm of \(x\) with base \(a\), where \(a>0,x>0\), and \(a≠1\) if
\(\log_{a}(a^x)=x\) and \(a^{\log_{a}x}=x\),
or,
\(y=\log _{a} x\) is equivalent to \(x=a^{y}\).
So the chart becomes:
|
Subtraction 'undoes' addition: |
\(x+3-3=x\) \(x-3+3=x\) |
| Division 'undoes' multiplication: |
\(\dfrac{1}{3}\cdot(3x)=x\) or \(\dfrac{3x}{3}=x\) \(3\cdot\left(\dfrac{x}{3}\right)=x\) |
| square root 'undoes' squaring (same button on calculator!) |
\((\sqrt{x})^2=x\) \(\sqrt{x^2}=x\) for \(x\geq 0\). |
|
logarithm 'undoes' exponential \(\ln x\) 'undoes' \(e^x\)? \(\log x\) 'undoes' \(10^x\)? and more generally \(\log_{a}x\) 'undoes' \(a^x\)? |
Notation: \(\ln e^x=x\) and \(e^{\ln x}=x\) \(\log 10^x=x\) and \(10^{\log x}=x\) \(\log_a a^x=x\) and \(a^{\log_a x}=x\) |
Converting Between Exponential and Logarithmic Form (DELETE???)
Since the equations \(y=\log _{a} x\) and \(x=a^{y}\) are equivalent, we can go back and forth between them. This will often be the method to solve some exponential and logarithmic equations. To help with converting back and forth let’s take a close look at the equations. See the figure below. Notice the positions of the exponent and base.
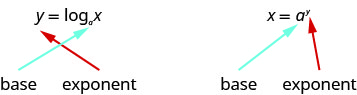
If we realize the logarithm is the exponent it makes the conversion easier. You may want to repeat, “base to the exponent give us the number.”
Convert to logarithmic form:
a. \(2^{3}=8\)
b. \(5^{1/2}=\sqrt{5}\)
c. \(\left(\dfrac{1}{2}\right)^{x}=\dfrac{1}{16}\)
Solution:
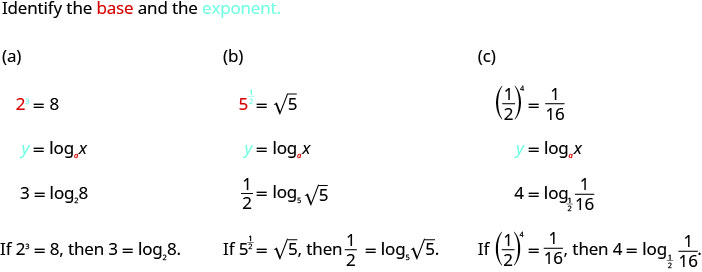
Convert to logarithmic form:
a. \(3^{2}=9\)
b. \(7^{1/2}=\sqrt{7}\)
c. \(\left(\dfrac{1}{3}\right)^{x}=\dfrac{1}{27}\)
- Answer
-
a. \(\log _{3} (9)=2\)
b. \(\log _{7} \left(\sqrt{7}\right)=\dfrac{1}{2}\)
c. \(\log _{1/3} \left(\dfrac{1}{27}\right)=x\)
Convert to logarithmic form:
a. \(4^{3}=64\)
b. \(4^{1/3}=\sqrt[3]{4}\)
c. \(\left(\dfrac{1}{2}\right)^{x}=\dfrac{1}{32}\)
- Answer
-
a. \(\log _{4} (64)=3\)
b. \(\log _{4} \left(\sqrt[3]{4}\right)=\dfrac{1}{3}\)
c. \(\log _{1/2} \left(\dfrac{1}{32}\right)=x\)
In the next example we do the reverse—convert logarithmic form to exponential form.
Convert to exponential form:
a. \(2=\log _{8} (64)\)
b. \(0=\log _{4} (1)\)
c. \(-3=\log _{10} \left(\dfrac{1}{1000}\right)\)
Solution:
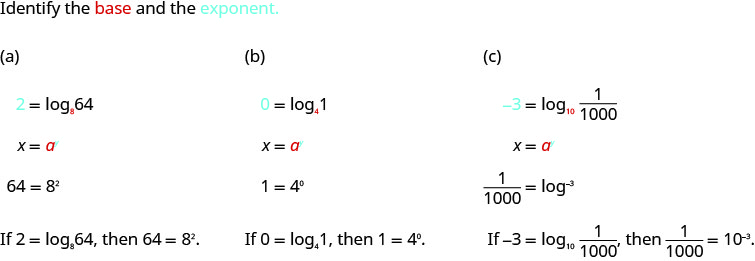
Convert to exponential form:
a. \(3=\log _{4}(64)\)
b. \(0=\log _{x} (1)\)
c. \(-2=\log _{10} \left(\dfrac{1}{100}\right)\)
- Answer
-
a. \(64=4^{3}\)
b. \(1=x^{0}\)
c. \(\dfrac{1}{100}=10^{-2}\)
Convert to exponential form:
a. \(3=\log _{3} (27)\)
b. \(0=\log _{x} (1)\)
c. \(-1=\log _{10} \left(\dfrac{1}{10}\right)\)
- Answer
-
a. \(27=3^{3}\)
b. \(1=x^{0}\)
c. \(\dfrac{1}{10}=10^{-1}\)
Evaluating Logarithmic Expressions
We can solve and evaluate logarithmic equations by using the technique of converting the equation to its equivalent exponential equation.
Evaluate:
a. \(\log _{6} (36)\)
b. \(\log _{4} (64)\)
c. \(\log _{1/2} \left(\dfrac{1}{8}\right)\)
Solution:
a.
\(\log _{6} 36\)
This is the power you need to raise 6 to in order to get 36. Since \(6^2=36\), this is 2!
So, \(\log _{6} 36=2\).
b.
\(\log _{4} 64\) is the power you need to raise 4 to to get 64.
Since \(4^3=64\), we see the power is 3.
Therefore, \(\log _{4} 64=3\).
c.
\(\log _{1/2} \left(\dfrac{1}{8}\right)\) is the power we need to raise \(\dfrac12\) to to get \(\dfrac18\).
But
\(\left(\dfrac{1}{2}\right)^{3}=\left(\dfrac{1}{8}\right)\)
Therefore \(\log _{1/2}\left( \dfrac{1}{8}\right)=3\).
Evaluate:
a. \(\log _{8} (64)\)
b. \(\log _{5} (125)\)
c. \(\log _{1/2} \left(\dfrac{1}{4}\right)\)
- Answer
-
a. \(2\)
b. \(3\)
c. \(2\)
Evaluate:
a. \(\log _{9} (81)\)
b. \(\log _{3} (243)\)
c. \(\log _{1/3} \left(\dfrac{1}{27}\right)\)
- Answer
-
a. \(2\)
b. \(5\)
c. \(3\)
When see an expression such as \(\log_{3}27\), we can find its exact value two ways. By inspection we realize it means “\(3\) to what power will be \(27\)”? Since \(3^{3}=27\), we know \(\log_{3}27=3\). An alternate way is to set the expression equal to \(x\) and then convert it into an exponential equation.
Find the exact value of each logarithm without using a calculator:
a. \(\log _{5} (25)\)
b. \(\log _{9} (3)\)
c. \(\log _{2} \left(\dfrac{1}{16}\right)\)
Solution:
a.
|
\(\log _{5} (25)\) |
|
| \(5\) to what power will be \(25\)? | 2 |
| Conclude | \(\log _{5} (25)=2\) |
Or
| \(\log _{5} (25)\) | |
| Set the expression equal to \(x\). | \(\log _{5} (25)=x\) |
| Change to exponential form. | \(5^{x}=25\) |
| Rewrite \(25\) as \(5^{2}\). | \(5^{x}=5^{2}\) |
| With the same base the exponents must be equal. | \(x=2\) |
| Conclude. | Therefore \(\log _{5} (25)=2\). |
b.
| \(\log _{9} (3)\) | |
| Set the expression equal to \(x\). | \(\log _{9} (3)=x\) |
| Change to exponential form. | \(9^{x}=3\) |
| Rewrite \(9\) as \(3^{2}\). | \(\left(3^{2}\right)^{x}=3^{1}\) |
| Simplify the exponents. | \(3^{2 x}=3^{1}\) |
| With the same base the exponents must be equal. | \(2 x=1\) |
| Solve the equation. | \(x=\dfrac{1}{2}\) |
| Conclude. | Therefore \(\log _{9} (3)=\dfrac{1}{2}\). |
c.
| \(\log _{2} \left(\dfrac{1}{16}\right)\) | |
| Set the expression equal to \(x\). |
\(\log _{2}\left(\dfrac{1}{16}\right)=x\) |
| Change to exponential form. | \(2^{x}=\dfrac{1}{16}\) |
| Rewrite \(16\) as \(2^{4}\). | \(2^{x}=\dfrac{1}{2^{4}}\) |
| With the same base the exponents must be equal. |
\(2^{x}=2^{-4}\) \(x=-4\) |
| Conclude. | Therefore \(\log _{2} \left(\dfrac{1}{16}\right)=-4\). |
Find the exact value of each logarithm without using a calculator:
a. \(\log _{12} (144)\)
b. \(\log _{4} (2)\)
c. \(\log _{2} \left(\dfrac{1}{32}\right)\)
- Answer
-
a. \(2\)
b. \(\dfrac{1}{2}\)
c. \(-5\)
Find the exact value of each logarithm without using a calculator:
a. \(\log _{9} (81)\)
b. \(\log _{8} (2)\)
c. \(\log _{3} \left(\dfrac{1}{9}\right)\)
- Answer
-
a. \(2\)
b. \(\dfrac{1}{3}\)
c. \(-2\)

In general we have expressions \(\ln x\), \(\log x\), and \(\log_a x\) for any value of \(x\) as can be approximated using your calculator (for now in the first two cases but also in general which we won't go into here).
We can therefore also have logarithmic expressions:
A logarithmic expression is an expression containing any of \(\ln x\), \(\log x\), and \(\log_a x\) with
\(x\) being replaced by any combinations of variables and numbers.
Using Logarithmic Models in Applications
There are many applications that are modeled by logarithmic expressions. We will first look at the logarithmic equation that gives the decibel (dB) level of sound. Decibels range from \(0\), which is barely audible to \(160\), which can rupture an eardrum. The \(10^{−12}\) in the formula represents the intensity of sound that is barely audible.
Decibel Level of Sound
The loudness level measured in decibels, of a sound of intensity, \(I\), measured in watts per square inch is
\(10 \log \left(\dfrac{I}{10^{-12}}\right)\)
Extended exposure to noise that measures \(85\) dB can cause permanent damage to the inner ear which will result in hearing loss. What is the decibel level of music coming through ear phones with intensity \(10^{−2}\) watts per square inch?
Solution:
|
\(10\log\left(\dfrac{I}{10^{-12}}\right)\) |
|
|---|---|
| Substitute in the intensity level, \(I\). |
\(10\log\left(\dfrac{10^{-2}}{10^{-12}}\right)\) |
| Simplify. |
\(10\log(10^{10})\) |
| Since \(\log \left(10^{10}\right)=10\). |
\(10\cdot 10\) |
| Multiply. |
\(100\) |
| The decibel level of music coming through earphones is \(100\) dB. |
What is the decibel level of one of the new quiet dishwashers with intensity \(10^{−7}\) watts per square inch?
- Answer
-
The quiet dishwashers have a decibel level of \(50\) dB.
What is the decibel level heavy city traffic with intensity \(10^{−3}\) watts per square inch?
- Answer
-
The decibel level of heavy traffic is \(90\) dB.
The magnitude \(R\) of an earthquake is measured by a logarithmic scale called the Richter scale. The model is \(\log I\), where \(I\) is the intensity of the shock wave. This model provides a way to measure earthquake intensity.
The magnitude of an earthquake is measured by \(\log I\), where \(I\) is the intensity of its shock wave.
In 1906, San Francisco experienced an intense earthquake with a magnitude of \(7.8\) on the Richter scale. Over \(80\)% of the city was destroyed by the resulting fires. In 2014, Los Angeles experienced a moderate earthquake that measured \(5.1\) on the Richter scale and caused $\(108\) million dollars of damage. Compare the intensities of the two earthquakes.
Solution:
To compare the intensities, we first need to convert the magnitudes to intensities using the log formula. Then we will set up a ratio to compare the intensities.
|
The logarithm of the intensity, \(I\), of the 1906 earthquake is 7.8, |
\(7.8=\log I\). |
|---|---|
| This means that 7.8 is the exponent of 10 needed to arrive at the Intensity: | \(I=10^{7.8}\) |
|
The magnitude of the intensity, \(J\) (we already used \(I\) for something else!), of the 2014 earthquake is |
\(5.1=\log J\) |
|
This means that 5.1 is the exponent with base 10 needed to arrive at the intensity \(J\): |
\(J=10^{5.1}\) |
| Form a ratio of the intensities. | \(\dfrac{\text { Intensity for } 1906}{\text { Intensity for } 2014}\) |
| Substitute in the values. | \(\dfrac{10^{7.8}}{10^{5.1}}\) |
| Divide by subtracting the exponents. | \(10^{2.7}\) |
| Evaluate. | \(501\) |
| The intensity of the 1906 earthquake was about \(501\) times the intensity of the 2014 earthquake. |
In 1906, San Francisco experienced an intense earthquake with a magnitude of \(7.8\) on the Richter scale. In 1989, the Loma Prieta earthquake also affected the San Francisco area, and measured \(6.9\) on the Richter scale. Compare the intensities of the two earthquakes.
- Answer
-
The intensity of the 1906 earthquake was about \(8\) times the intensity of the 1989 earthquake.
In 2014, Chile experienced an intense earthquake with a magnitude of \(8.2\) on the Richter scale. In 2014, Los Angeles also experienced an earthquake which measured \(5.1\) on the Richter scale. Compare the intensities of the two earthquakes.
- Answer
-
The intensity of the earthquake in Chile was about \(1,259\) times the intensity of the earthquake in Los Angeles.
1. How is approximating the solution to \(10^x=2\) similar to solving \(x^2=5\) on a calculator?
2. What is \(\log_b(a)\)?
3. In the definition of \(\log_b(a)\), why don’t we allow \(b\) to be \(1\)?
Evaluate \(\log_{1/2}(25)\).
Key Concepts
- Evaluation of logarithms
- (Optional) Basic shape of the graph of \(y=\log _{a} x\) for various \(a\) values.
- Decibel Level of Sound: The loudness level measured in decibels, of a sound of intensity, \(I\), measured in watts per square inch is \(10 \log \left(\dfrac{I}{10^{-12}}\right)\).
- Earthquake Intensity: The magnitude of an earthquake is measured by \(\log I\), where \(I\) is the intensity of its shock wave.
Glossary
- common logarithm
- \(\log_{10}x=\log x\) is the common logarithm, where \(x>0\), which is the exponent with base 10 needed to evaluate to \(x\).
-
Equivalently,
\(y=\log x\) is equivalent to \(x=10^{y}\)
- logarithm
- For \(a>0, a\not=1\) and \(x>0\), the logarithm of \(x\) with base \(a\), \(\log _{a} x\) is the exponent with base \(a\) needed to evaluate to \(x\). Or equivalently, \(y=\log _{a} x\) is equivalent to \(x=a^{y}\)
- natural logarithm
- \(\log_{e}x=\ln x\) is the natural logarithm, where \(x>0\). It is the exponent needed with base \(e\) to evaluate to \(x\), or, equaivalently,
\(y=\ln x\) is equivalent to \(x=e^{y}\)


