5.2: Appendix B- Decimal Numbers
- Page ID
- 136544
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Consider the number \(23.7456\). Each digit occupies a 'place". The 2 is in the tens place, the three in the ones place, the 7 in the tenths place, the 4 in the hundredths place, the 5 in the thousandths place, and the 6 in the ten thousandths place. Why? Because:
\[23.7456=2 \cdot 10+3 \cdot 1+7 \cdot \dfrac{1}{10}+4 \cdot \dfrac{1}{100}+5 \cdot \dfrac{1}{1000}+6 \cdot \dfrac{1}{10,000}\nonumber\]
Rounding
Rounding is associated with cutting or truncating a number, and that the rounding compensates for the lost tail of the number. For example, to round a given number to the nearest tenth, we look one digit to the right of the tenths place (the hundredths place) and if it is greater than or equal to 5, we add one to the tenths place and remove all the digits to the right, otherwise we leave the tenths place as it is and remove all the digits to the right.
Example \(\PageIndex{1}\)
- 234.45 rounded to the nearest ten is 230.
- 45.6 rounded to the nearest ones (whole number) is 46.
- 34.555 rounded to the nearest tenth is 34.6.
- 34.54 rounded to the nearest tenth is 34.5.
- 34.95 rounded to the nearest tenth is 35.0.
- 34.554 rounded to the nearest hundredth is 34.55.
- 56.7874778 rounded to the nearest ten-thousandth is 56.7875
Adding and Subtracting Decimal Numbers
To add decimals, we line up the decimal points, and wherever there is a missing digit, we fill it in with a zero. For example, add 45.23 and 2.3:
\[\begin{array}{rrrrr}
4 & 5 & . & 2 & 3 \\
+ & 2 & . & 3 & 0 \\
\hline 4 & 7 & . & 5 & 3
\end{array} \nonumber\]
Subtracting is similar. To subtract 45.23 from 2.3 we first note that the answer should be negative and proceed to subtract 2.3 from 45.23:
\[\begin{array}{lllll}
4 & 5 & . & 2 & 3 \\
- & 2 & . & 3 & 0 \\
\hline 4 & 2 & . & 9 & 3
\end{array} \nonumber\]
So, the answer of \(2.3-45.23=-42.93\)
Example 3.2
- \(2.4+32.032=34.432\)
- \(3.44+12.035=15.475\)
- \(34.3-0.05=34.25\)
- \(6.3-9.72=-3.42\)
Multiplying and Dividing Decimal Numbers
Multiplying and Dividing Decimal Numbers by 10, 100, 1000, . . .
We first look at the special multiplication of decimals by 10, 100, 1000, . . .
\[\begin{align*} 12.415 &\times 10 &=124.15 \\ 12.415 &\times 100 &=1241.5 \\ 12.415 &\times 1000 &=12415 \end{align*} \nonumber\]
When we multiply by 10 we move the decimal point to the right one place (because 10 has one decimal place). Multiplying by 100 moves the decimal point two places (because 100 has two decimal places), etc.
\(\begin{array}{l}
12.415 \div 10=1.2415 \\
12.415 \div 100=0.12415 \\
12.415 \div 1000=0.012415
\end{array}\)
When we divide by 10 we move the decimal point to the left one place (because 10 has one decimal place). Dividing by 100 moves the decimal point to the left two places (because 100 has two decimal places), etc.
\(10^{n}\) notation
\[\begin{array}{l}
10=10^{1} \\
100=10 \times 10=10^{2} \\
1000=10 \times 10 \times 10=10^{3}
\end{array}\nonumber\]
Notice that the exponent of 10 in \(10^{n}\) notation reflects the number of zeros! So, \(10000=10^{4}(4 \text { zeros, exponent is } 4)\) and \(100,000=10^{5}, \ldots\)
Multiplying by \(10^{n}\)
Multiplying a decimal number by \(10^{n}\) moves the decimal place \(n\) spots to the right. For example:
\[\begin{array}{l}
5.435 \times 10=54.35 \\
5.435 \times 100=543.5 \\
5.435 \times 10000=54350
\end{array}\nonumber\]
Multiplying Decimal Numbers
To multiply two decimal numbers, we multiply as if there is no decimal point, then place a decimal point as described in the next example.
Example 3.3
Multiply 5.4 by 1.21.
Solution
\(\begin{array}{rrrr}
& & 1 & 2 & 1 \\
\times & & & 5 & 4 \\
\hline & & 4 & 8 & 4 \\
& 6 & 0 & 5 & 0 \\
\hline & 6 & 5 & 3 & 4
\end{array}\)
Now, to write out the answer, we notice that there are two digits after the decimal point in the first number \(1.21,\) and one digit after the decimal point in the second number \(5.4 .\) The product then should have 3 digits after the decimal point. So, \(5.4 \times 1.21=6.534\)
Example 3.4
Multiply 3.72 by 13.
Solution
\(\begin{array}{rrrr}
& & 3 & 7 & 2 \\
\times & & & 1 & 3 \\
\hline & 1 & 1 & 1 & 6 \\
& 3 & 7 & 2 & 0 \\
\hline & 4 & 8 & 3 & 6
\end{array}\)
Now, to write out the answer, we notice that there are two digits after the decimal point in 3.72 while 13 has no decimal part. The product then should have 2 digits after the decimal point: \(3.72 \times 13=48.36\)
Dividing Decimal Numbers
Dividing a decimal number is a lot like dividing a whole number, except you use the position of the decimal point in the dividend to determine the decimal places in the result.
Example 3.5
- \(6.5 \div 2\)
- \(55.318 \div 3.4\)
Solution
a) Divide as usual:
If the divisor does not go into the dividend evenly, add zeros to the right of the last digit in the dividend and continue until either the remainder is 0, or a repeating pattern appears. Place the position of the decimal point in your answer directly above the decimal point in the dividend.
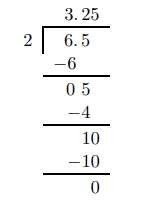
b)
If the divisor in not a whole number, move the decimal point in the divisor all the way to the right (to make it a whole number). Then move the decimal point in the dividend the same number of places.
In this example, move the decimal point one place to the right for the divisor from 3.4 to \(34 .\) Therefore, also move the decimal point one place to the right for the dividend, from 55.318 to 553.18 .
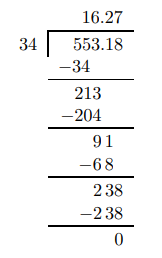
Converting Decimals to Fractions
To convert a decimal to a fraction is as simple as recognizing the place of the right most digit.
Example: Note that in the number \(2.45,\) the right most digit 5 is in the hundredths place so \(2.45=\dfrac{245}{100}=\dfrac{49}{20}\) or \(2 \dfrac{9}{20}\)
Example 3.6
Here are a few more examples:
- \(1.2=\dfrac{12}{10}=\dfrac{6}{5}\) or \(1 \dfrac{1}{5}\)
- \(0.0033=\dfrac{33}{10,000}\)
- \(0.103=\dfrac{103}{1000}\)
Converting Fractions to Decimals
To convert a fraction to a decimal you simply perform long division.
Example 3.7
Convert the given fraction to a decimal:
- \(\dfrac{4}{5}=4 \div 5=0.8\)
- \(3 \dfrac{4}{5}=3+4 \div 5=3.8\)
- \(\dfrac{13}{2}=6 \dfrac{1}{2}=6+1 \div 2=6.5\)
- (round to the nearest tenth) \(\dfrac{3}{7}=3 \div 7=0.42857 \cdots \approx 0.4\)
Converting Decimals to Percents and Percents to Decimals
"Percent" comes from Latin and means per hundred. We use the sign \% for Por example, if you know that \(25 \%\) of the students speak Spanish fluently, it means that 25 of every 100 students speak fluent Spanish. Presented as fraction, it would be \(\dfrac{25}{100}\) and as a decimal 0.25.
Example 3.8
Convert the given percent to fraction then to a decimal:
- \(17 \%\) is \(\dfrac{17}{100}=0.17\)
- \(31 \%\) is \(\dfrac{31}{100}=0.31\)
- \(23.44 \%\) is \(\dfrac{23.44}{100}=0.2344\)
Example 3.9
Convert the given decimal to a fraction then to percent:
- \(0.55=\dfrac{55}{100}\) which is \(55 \%\)
- \(8.09=\dfrac{809}{100}\) which is \(809 \%\)
- \(98.08=\dfrac{9808}{100}\) which is \(9808 \%\)
- \(0.5=\dfrac{50}{100}\) which is \(50 \%\)
Exit Problem
Divide: \(782.56 \div 3.2\)


