1.4: Chapter 1 Review Exercises

Last updated
Save as PDF

Page ID: 66283

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Chapter Review Exercises

Graph Linear Equations in Two Variables

Plot Points in a Rectangular Coordinate System

In the following exercises, plot each point in a rectangular coordinate system.

1. ⓐ $(−1,−5)$
ⓑ $(−3,4)$
ⓒ $(2,−3)$
ⓓ $(1,\frac{5}{2})$

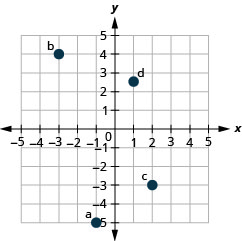
Answer: $This figure shows points plotted on the x y-coordinate plane. The x and y axes run from negative 5 to 5. The point labeled a is 1 units to the left of the origin and 5 units below the origin and is located in quadrant III. The point labeled b is 3 units to the left of the origin and 4 units above the origin and is located in quadrant II. The point labeled c is 2 units to the right of the origin and 3 units below the origin and is located in quadrant IV. The point labeled d is 1 unit to the right of the origin and 2.5 units above the origin and is located in quadrant I.$

2. ⓐ $(−2,0)$
ⓑ $(0,−4)$
ⓒ $(0,5)$
ⓓ $(3,0)$

In the following exercises, determine which ordered pairs are solutions to the given equations.

3. $5x+y=10$;

ⓐ $(5,1)$
ⓑ $(2,0)$
ⓒ $(4,−10)$

Answer: ⓑ, ⓒ

4. $y=6x−2$;

ⓐ $(1,4)$
ⓑ $(13,0)$
ⓒ $(6,−2)$

Graph a Linear Equation by Plotting Points

In the following exercises, graph by plotting points.

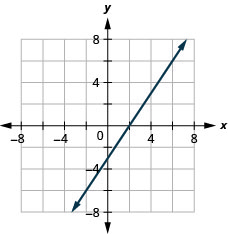
5. $y=4x−3$

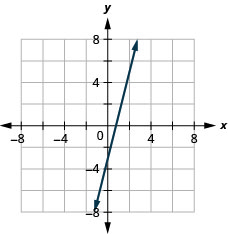
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 1, negative 7), (0, negative 3), (1, negative 1), and (2, 3).$

6. $y=−3x$

7. $y=\frac{1}{2}x+3$

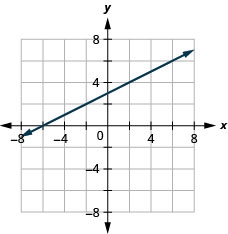
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 6, 0), (0, 3), (2, 4), and (4, 5).$

8. $y=−\frac{4}{5}|x−1$

9. $x−y=6$

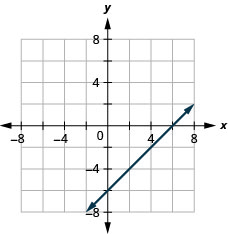
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 1, negative 7), (0, negative 6), (3, negative 3), and (6, 0).$

10. $2x+y=7$

11. $3x−2y=6$

Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 2, negative 6), (0, negative 3), (2, 0), and (4, 3).$

Graph Vertical and Horizontal lines

In the following exercises, graph each equation.

12. $y=−2$

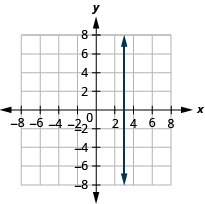
13. $x=3$

Answer: $This figure shows a vertical straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (3, negative 1), (3, 0), and (3, 1).$

In the following exercises, graph each pair of equations in the same rectangular coordinate system.

14. $y=−2x$ and $y=−2$

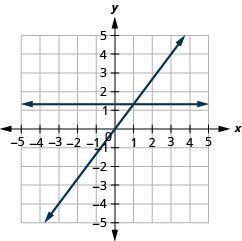
15. $y=\frac{4}{3}x$ and $y=\frac{4}{3}$

Answer: $The figure shows the graphs of a straight horizontal line and a straight slanted line on the same x y-coordinate plane. The x and y axes run from negative 5 to 5. The horizontal line goes through the points (0, 4 divided by 3), (1, 4 divided by 3), and (2, 4 divided by 3). The slanted line goes through the points (0, 0), (1, 4 divided by 3), and (2, 8 divided by 3).$

Find x- and y-Intercepts

In the following exercises, find the x- and y-intercepts.

16.
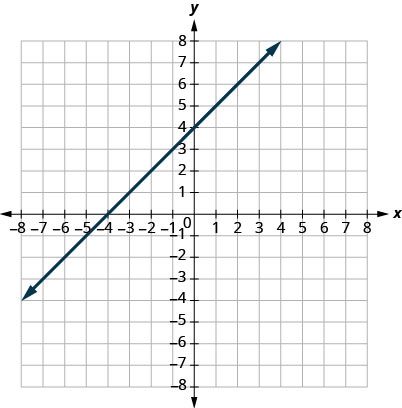
$The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 6, negative 2), (negative 4, 0), (negative 2, 2), (0, 4), (2, 6), and (4, 8).$

17.
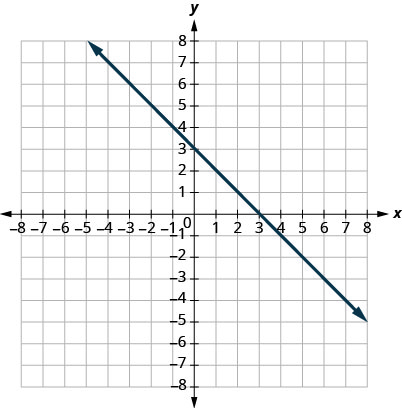
$The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 2, 5), (negative 1, 4), (0, 3), (3, 0), and (6, negative 3).$

Answer: $(0,3)(3,0)$

In the following exercises, find the intercepts of each equation.

18. $x−y=−1$

19. $x+2y=6$

Answer: $(6,0),\space (0,3)$

20. $2x+3y=12$

21. $y=\frac{3}{4}x−12$

Answer: $(16,0),\space (0,−12)$

22. $y=3x$

Graph a Line Using the Intercepts

In the following exercises, graph using the intercepts.

23. $−x+3y=3$

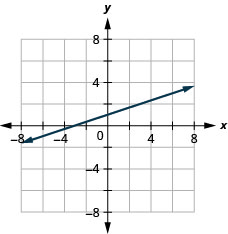
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 3, 0), (0, 1), (3, 2), and (6, 3).$

24. $x−y=4$

25. $2x−y=5$

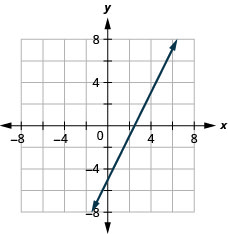
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (0, negative 5), (1, negative 3), (2, negative 1), and (3, 1).$

26. $2x−4y=8$

27. $y=4x$

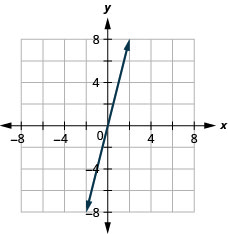
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 1, 4), (0, 0), and (1, negative 4).$

Slope of a Line

Find the Slope of a Line

In the following exercises, find the slope of each line shown.

28.
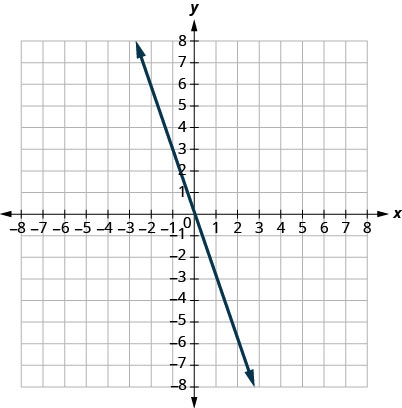
$This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line goes through the points (0, 0) and (1, negative 3).$

29.
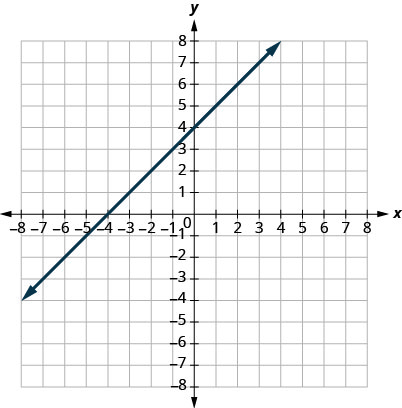
$This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line goes through the points (negative 4, 0) and (0, 4).$

Answer: 1

30.
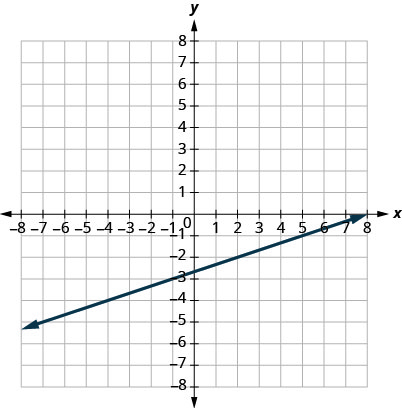
$This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line goes through the points (negative 4, negative 4) and (2, negative 2).$

31.
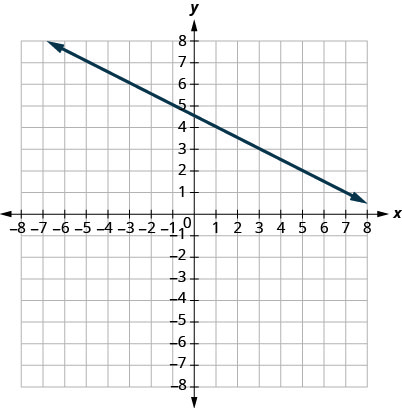
$This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line goes through the points (1, 4) and (5, 2).$

Answer: $−12$

In the following exercises, find the slope of each line.

32. $y=2$

33. $x=5$

Answer: undefined

34. $x=−3$

35. $y=−1$

Answer: 0

Use the Slope Formula to find the Slope of a Line between Two Points

In the following exercises, use the slope formula to find the slope of the line between each pair of points.

36. $(−1,−1),(0,5)$

37. $(3.5),(4,−1)$

Answer: $−6$

38. $(−5,−2),(3,2)$

39. $(2,1),(4,6)$

Answer: $52$

Graph a Line Given a Point and the Slope

In the following exercises, graph each line with the given point and slope.

40. $(2,−2);\space m=52$

41. $(−3,4);\space m=−13$

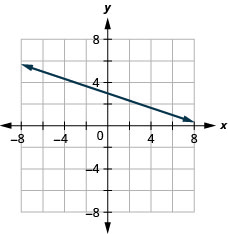
Answer: $This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (negative 3, 4) and (0, 3).$

42. $x$-intercept $−4; m=3$

43. $y$-intercept $1; m=−34$

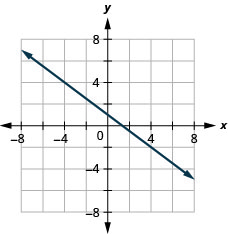
Answer: $This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (0, 1) and (4, negative 2).$

Graph a Line Using Its Slope and Intercept

In the following exercises, identify the slope and $y$-intercept of each line.

44. $y=−4x+9$

45. $y=53x−6$

Answer: $m=53;\space (0,−6)$

46. $5x+y=10$

47. $4x−5y=8$

Answer: $m=45;\space (0,−85)$

In the following exercises, graph the line of each equation using its slope and y-intercept.

48. $y=2x+3$

49. $y=−x−1$

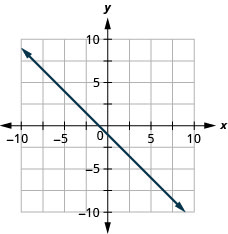
Answer: $This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (0, negative 1) and (1, negative 2).$

50. $y=−25x+3$

51. $4x−3y=12$

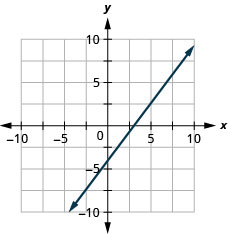
Answer: $This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (0, negative 4) and (3, 0).$

In the following exercises, determine the most convenient method to graph each line.

52. $x=5$

53. $y=−3$

Answer: horizontal line

54. $2x+y=5$

55. $x−y=2$

Answer: intercepts

56. $y=22x+2$

57. $y=34x−1$

Answer: plotting points

Graph and Interpret Applications of Slope-Intercept

58. Katherine is a private chef. The equation $C=6.5m+42$ models the relation between her weekly cost, C, in dollars and the number of meals, m, that she serves.

ⓐ Find Katherine’s cost for a week when she serves no meals.
ⓑ Find the cost for a week when she serves 14 meals.
ⓒ Interpret the slope and C-intercept of the equation.
ⓓ Graph the equation.

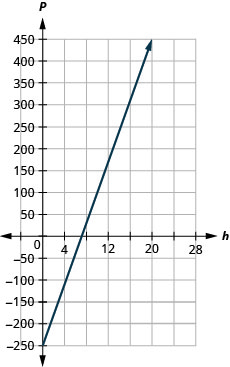
59. Marjorie teaches piano. The equation $P=35h−250$ models the relation between her weekly profit, P, in dollars and the number of student lessons, s, that she teaches.

ⓐ Find Marjorie’s profit for a week when she teaches no student lessons.
ⓑ Find the profit for a week when she teaches 20 student lessons.
ⓒ Interpret the slope and P-intercept of the equation.
ⓓ Graph the equation.

Answer

ⓐ $−$250$
ⓑ $$450$
ⓒ The slope, 35, means that Marjorie’s weekly profit, P, increases by $35 for each additional student lesson she teaches.
The P-intercept means that when the number of lessons is 0, Marjorie loses $250.
ⓓ

$This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 4 to 28. The y-axis runs from negative 250 to 450. The line goes through the points (0, negative 250) and (20, 450).$

Use Slopes to Identify Parallel and Perpendicular Lines

In the following exercises, use slopes and $y$-intercepts to determine if the lines are parallel, perpendicular, or neither.

60. $4x−3y=−1;\quad y=43x−3$

61. $y=5x−1;\quad 10x+2y=0$

Answer: neither

62. $3x−2y=5;\quad 2x+3y=6$

63. $2x−y=8;\quad x−2y=4$

Answer: not parallel

Find the Equation of a Line

Find an Equation of the Line Given the Slope and y-Intercept

In the following exercises, find the equation of a line with given slope and y-intercept. Write the equation in slope–intercept form.

64. Slope $\frac{1}{3}$ and $y$-intercept $(0,−6)$

65. Slope $−5$ and $y$-intercept $(0,−3)$

Answer: $y=−5x−3$

66. Slope $0$ and $y$-intercept $(0,4)$

67. Slope $−2$ and $y$-intercept $(0,0)$

Answer: $y=−2x$

In the following exercises, find the equation of the line shown in each graph. Write the equation in slope–intercept form.

68.
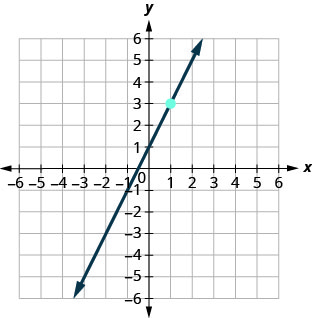
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, 1), (1, 3), and (2, 5).$

69.
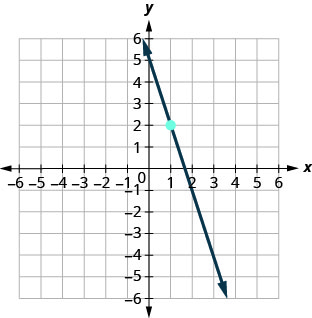
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, 5), (1, 2), and (2, negative 1).$

Answer: $y=−3x+5$

70.
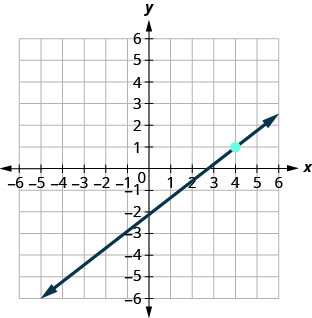
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, negative 2), (4, 1), and (8, 4).$

71.
$This figure has a graph of a horizontal straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, negative 4), (1, negative 4), and (2, negative 4).$

Answer: $y=−4$

Find an Equation of the Line Given the Slope and a Point

In the following exercises, find the equation of a line with given slope and containing the given point. Write the equation in slope–intercept form.

72. $m=−\frac{1}{4}$, point $(−8,3)$

73. $m=\frac{3}{5}$, point $(10,6)$

Answer: $y=\frac{3}{5}x$

74. Horizontal line containing $(−2,7)$

75. $m=−2$, point $(−1,−3)$

Answer: $y=−2x−5$

Find an Equation of the Line Given Two Points

In the following exercises, find the equation of a line containing the given points. Write the equation in slope–intercept form.

76. $(2,10)$ and $(−2,−2)$

77. $(7,1)$ and $(5,0)$

Answer: $y=\frac{1}{2}x−\frac{5}{2}$

78. $(3,8)$ and $(3,−4)$

79. $(5,2)$ and $(−1,2)$

Answer: $y=2$

Find an Equation of a Line Parallel to a Given Line

In the following exercises, find an equation of a line parallel to the given line and contains the given point. Write the equation in slope–intercept form.

80. line $y=−3x+6$, point $(1,−5)$

81. line $2x+5y=−10$, point $(10,4)$

Answer: $y=−\frac{2}{5}x+8$

82. line $x=4$, point $(−2,−1)$

83. line $y=−5$, point $(−4,3)$

Answer: $y=3$

Find an Equation of a Line Perpendicular to a Given Line

In the following exercises, find an equation of a line perpendicular to the given line and contains the given point. Write the equation in slope–intercept form.

84. line $y=−\frac{4}{5}x+2$, point $(8,9)$

85. line $2x−3y=9$, point $(−4,0)$

Answer: $y=−\frac{3}{2}x−6$

86. line $y=3$, point $(−1,−3)$

87. line $x=−5$ point $(2,1)$

Answer: $y=1$

Practice Test

1. Plot each point in a rectangular coordinate system.

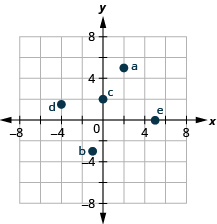
Answer: $This figure shows points plotted on the x y-coordinate plane. The x and y axes run from negative 10 to 10. The point labeled a is 2 units to the right of the origin and 5 units above the origin and is located in quadrant I. The point labeled b is 1 unit to the left of the origin and 3 units below the origin and is located in quadrant III. The point labeled c is 2 units above the origin and is located on the y-axis. The point labeled d is 4 units to the left of the origin and 1.5 units above the origin and is located in quadrant II. The point labeled e is 5 units to the right of the origin and is located on the x-axis.$

2. Which of the given ordered pairs are solutions to the equation $3x−y=6$?

3. Find the slope of each line shown.

ⓐ

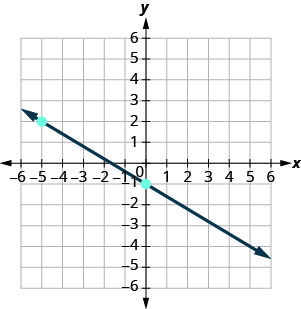
$The figure has a straight line graphed on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (negative 5, 2) (0, negative 1), and (5, negative 4).$

ⓑ

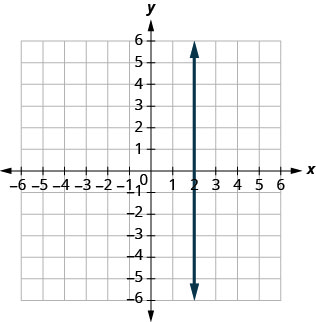
$The figure has a straight vertical line graphed on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (2, 0) (2, negative 1), and (2, 1).$

Answer: ⓐ $−\frac{3}{5}$ ⓑ undefined

4. Find the slope of the line between the points $(5,2)$ and $(−1,−4)$.

5. Graph the line with slope $\frac{1}{2}$ containing the point $(−3,−4)$.

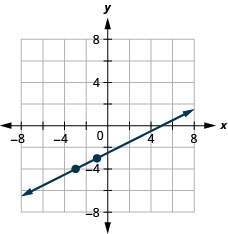
Answer: $The figure has a straight line graphed on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (negative 3, negative 4) (negative 1, negative 3), and (1, negative 2).$

6. Find the intercepts of $4x+2y=−8$ and graph.

Graph the line for each of the following equations.

7. $y=\frac{5}{3}x−1$

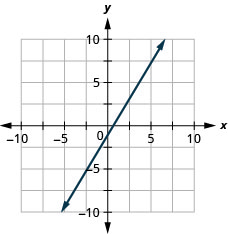
Answer: $The figure has a straight line graphed on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (negative 3, negative 6) (0, negative 1), and (3, 4).$

8. $y=−x$

9. $y=2$

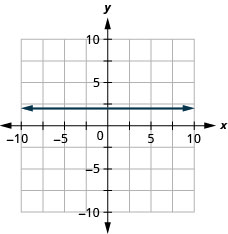
Answer: $The figure has a straight horizontal line graphed on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (negative 1, 2) (0, 2), and (1, 2).$

Find the equation of each line. Write the equation in slope-intercept form.

10. slope $−\frac{3}{4}$ and $y$-intercept $(0,−2)$

11. $m=2$, point $(−3,−1)$

Answer: $y=2x+5$

12. containing $(10,1)$ and $(6,−1)$

13. perpendicular to the line $y=\frac{5}{4}x+2$, containing the point $(−10,3)$

Answer: $y=−\frac{4}{5}x−5$