4.5: Polynomial Equations
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Use the Zero Product Property
- Solve quadratic equations by factoring
- Solve polynomial equations
- Solve applications modeled by polynomial equations
Before you get started, take this readiness quiz.
- Solve: 5y−3=0.
- Factor completely: n3−9n2−22n.
- If f(x)=8x−16, find f(3) and solve f(x)=0.
Polynomial Equations
We have spent considerable time learning how to factor polynomials. We will now look at polynomial equations and solve them using factoring, if possible.
- A polynomial equation is an equation that contains a polynomial expression.
- The solution of a polynomial equation is an assignment of the values to the variables that make the equation true; so substituting the values for the variables gives a true statement.
- The degree of the polynomial equation is the highest degree among all the terms appearing in the equation.
We have already solved polynomial equations of degree one. Polynomial equations of degree one are linear equations of the form ax+b=c.
We are now going to solve polynomial equations of degree two. A polynomial equation of degree two is called a quadratic equation. Listed below are some examples of quadratic equations:
x2+5x+6=0,3y2=−4y+10,64u2−81=0,n(n+1)=42.
The last equation doesn’t appear to have the variable squared, but when we simplify the expression on the left we will get n2+n.
The general form of a quadratic equation is ax2+bx+c=0, with a≠0. (If a=0, then 0⋅x2=0 and we are left with no quadratic term.)
An equation of the form ax2+bx+c=0 is called a quadratic equation where a,b, and c are real numbers and a≠0.
A polynomial and a polynomial equation are not the same. Here are some examples.
| Polynomial(s) | Polynomial Equation |
| 2x+1, 0 | 2x+1=0 |
| x2, x−2 | x2=x−2 |
| 3x2+5x−1, 0 | 3x2+5x−1=0 |
Note that x2+5x=x(x+5) is not a polynomial equation that we aim to solve. This is an identity of polynomials that was developed in the process of factoring the GCF out.
It does not make sense to "solve a polynomial." We can only solve equations. For example, we cannot solve 2x+1 as there is no statement to assess. Whereas 2x+1=0 is either true or false for a particular value of x. Below we check whether or not some values of x are solutions to the equation 2x+1=0.
| x | True or False | Solution or Not a Solution |
| 5 | 2⋅5+1=0 is false | Not a Solution |
| 0 | 2⋅0+1=0 is false | Not a Solution |
| −12 | 2⋅(−12)+1=0 is true | Solution |
To solve quadratic equations we need methods different from the ones we used in solving linear equations. We will look at one method here and then several others in a later chapter.
Use the Zero Product Property
We will first solve some quadratic equations by using the Zero Product Property. The Zero Product Property says that if the product of two quantities is zero, then at least one of the quantities is zero. The only way to get a product equal to zero is to multiply by zero itself.
If ab=0, then a=0 or b=0.
We will now use the Zero Product Property to solve a quadratic equation.
Solve (5n−2)(6n−1)=0.
- Solution
-



Solve (3m−2)(2m+1)=0.
- Answer
-
m=23, m=−12
Solve (4p+3)(4p−3)=0.
- Answer
-
p=−34, p=34
- Set each factor equal to zero.
- Solve the linear equations.
- Optional: Check answer to see if a mistake has been made.
Solve Quadratic Equations by Factoring
The Zero Product Property works very nicely to solve quadratic equations. The quadratic equation must be factored, with zero isolated on one side. So be sure to start with the quadratic equation in standard form, ax2+bx+c=0. Then factor the expression on the left.
Solve 2y2=13y+45.
- Solution
-

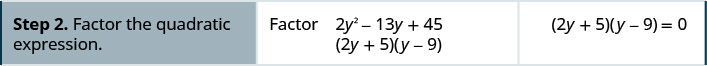


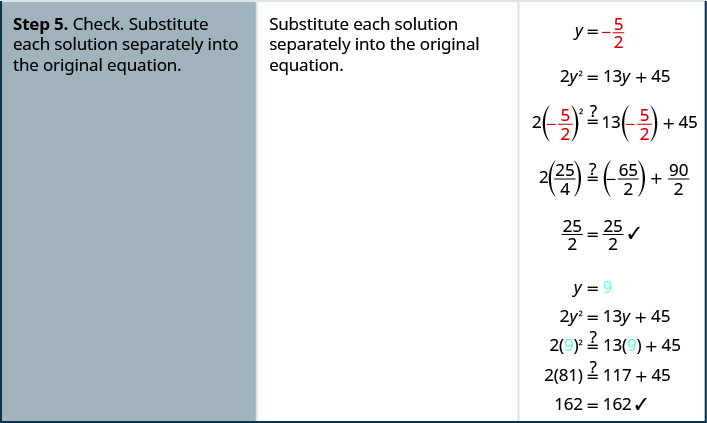
Solve 3c2=10c−8.
- Answer
-
c=2, c=43
Solve 2d2−5d=3.
- Answer
-
d=3, d=−12
- Write the quadratic equation in standard form, ax2+bx+c=0.
- Factor the quadratic expression.
- Use the Zero Product Property.
- Solve the linear equations.
- Optional: Check answer by substituting each solution separately into the original equation to see if a mistake has been made.
Before we factor, we must make sure the quadratic equation is in standard form.
Solving quadratic equations by factoring will make use of all the factoring techniques we have learned in this chapter! Do we recognize the special product pattern in the next example?
Solve 169q2=49.
- Solution
-
169q2=49Write the quadratic equation in standard form.169q2−49=0Factor. It is a difference of squares.(13q−7)(13q+7)=0Use the Zero Product Property to set each factor to 0.Solve each equation.13q−7=013q+7=013q=713q=−7q=713q=−713Check the answers.The check is left as an exercise.
Solve 25p2=49.
- Answer
-
p=75,p=−75
Solve 36x2=121.
- Answer
-
x=116,x=−116
In the next example, the left side of the equation is factored, but the right side is not zero. In order to use the Zero Product Property, one side of the equation must be zero. We’ll multiply the factors and then write the equation in standard form.
Solve (3x−8)(x−1)=3x.
- Solution
-
(3x−8)(x−1)=3xMultiply the binomials.3x2−11x+8=3xWrite the quadratic equation in standard form.3x2−14x+8=0Factor the trinomial.(3x−2)(x−4)=0Use the Zero Product Property to set each factor to 0.Solve each equation.3x−2=0x−4=03x=2x=4x=23Check the answers.The check is left as an exercise.
Solve (2m+1)(m+3)=12m.
- Answer
-
m=1, m=32
Solve (k+1)(k−1)=8.
- Answer
-
k=3, k=−3
In the next example, when we factor the quadratic equation we will get three factors. However the first factor is a constant. We know that factor cannot equal 0.
Solve 3x2=12x+63.
- Solution
-
3x2=12x+63Write the quadratic equation in standard form.3x2−12x−63=0Factor the greatest common factor first.3(x2−4x−21)=0Factor the trinomial.3(x−7)(x+3)=0Use the Zero Product Property to set each factor to 0.Solve each equation.3≠0x−7=0x+3=03≠0x=7x=−3Check the answers.The check is left as an exercise.
Solve 18a2−30=−33a.
- Answer
-
a=−52,a=23
Solve 123b=−6−60b2.
- Answer
-
b=−2, b=−120
The Zero Product Property also applies to the product of three or more factors. If the product is zero, at least one of the factors must be zero. We can solve some equations of degree greater than two by using the Zero Product Property, just like we solved quadratic equations.
Solve 9m3+100m=60m2.
- Solution
-
9m3+100m=60m2Bring all the terms to one side so that the other side is zero.9m3−60m2+100m=0Factor the greatest common factor first.m(9m2−60m+100)=0Factor the trinomial.m(3m−10)2=0Use the Zero Product Property to set each factor to 0.Solve each equation.m=03m−10=0m=0m=103Check your answers.The check is left to you.
Solve 8x3=24x2−18x.
- Answer
-
x=0, x=32
Solve 16y2=32y3+2y.
- Answer
-
y=0, y=14
Solve Equations with Polynomials
As our study of polynomials continues, it will often be important to know when a polynomial equals another polynomial. Our work with the Zero Product Property will be help us find these answers.
Solve Applications Modeled by Polynomial Equations
The problem-solving strategy we used earlier for applications that translate to linear equations will work just as well for applications that translate to polynomial equations. We will copy the problem-solving strategy here so we can use it for reference.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
- Solve the equation using appropriate algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
We will start with a number problem to get practice translating words into a polynomial equation.
The product of two consecutive odd integers is 323. Find the integers.
- Solution
-
Step 1. Read the problem.Step 2. Identify what we are looking for.We are looking for two consecutive integers.Step 3. Name what we are looking for.Let n= the first integer.n+2= next consecutive odd integerStep 4. Translate into an equation. Restate theproblem in a sentence.The product of the two consecutive oddintegers is 323.n(n+2)=323Step 5. Solve the equation.n2+2n=323Bring all the terms to one side.n2+2n−323=0Factor the trinomial.(n−17)(n+19)=0Use the Zero Product Property.Solve the equations.n−17=0n+19=0n=17n=−19
There are two values for n that are solutions to this problem. So there are two sets of consecutive odd integers that will work.If the first integer is n=17If the first integer is n=−19then the next odd integer isthen the next odd integer isn+2n+217+2−19+219−1717,19−17,−19Step 6. Check the answer.The results are consecutive odd integers17, 19 and −19, −17.17·19=323✓−19(−17)=323✓Both pairs of consecutive integers are solutions.Step 7. Answer the questionThe consecutive integers are 17,19 and −19,−17.
The product of two consecutive odd integers is 255. Find the integers.
- Answer
-
−15,−17 and 15,17
The product of two consecutive odd integers is 483 Find the integers.
- Answer
-
−23,−21 and 21,23
Were you surprised by the pair of negative integers that is one of the solutions to the previous example? The product of the two positive integers and the product of the two negative integers both give positive results.
In some applications, negative solutions will result from the algebra, but will not be realistic for the situation.
A rectangular bedroom has an area 117 square feet. The length of the bedroom is four feet more than the width. Find the length and width of the bedroom.
- Solution
-
Step 1. Read the problem. In problems involving
geometric figures, a sketch can help you visualize
the situation.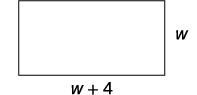
Step 2. Identify what you are looking for. We are looking for the length and width. Step 3. Name what you are looking for. Let w= the width of the bedroom. The length is four feet more than the width. w+4= the length of the garden Step 4. Translate into an equation. Restate the important information in a sentence. The area of the bedroom is 117 square feet. Use the formula for the area of a rectangle. A=l·w Substitute in the variables. 117=(w+4)w Step 5. Solve the equation Distribute first. 117=w2+4w Get zero on one side. 117=w2+4w Factor the trinomial. 0=w2+4w−117 Use the Zero Product Property. 0=(w2+13)(w−9) Solve each equation. 0=w+130=w−9 Since w is the width of the bedroom, it does not
make sense for it to be negative. We eliminate that value for w.w=−13 w=9 w=9 The width is 9 feet. Find the value of the length. w+4
9+4
13 The length is 13 feet.Step 6. Check the answer.
Does the answer make sense?
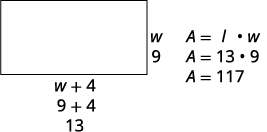
Yes, this makes sense.Step 7. Answer the question. The width of the bedroom is 9 feet and
the length is 13 feet.
A rectangular sign has area 30 square feet. The length of the sign is one foot more than the width. Find the length and width of the sign.
- Answer
-
The width is 5 feet and length is 6 feet.
A rectangular patio has area 180 square feet. The width of the patio is three feet less than the length. Find the length and width of the patio.
- Answer
-
The length of the patio is 12 feet and the width 15 feet.
In the next example, we will use the Pythagorean Theorem (a2+b2=c2). This formula gives the relation between the legs and the hypotenuse of a right triangle.
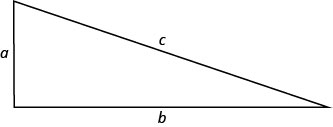
We will use this formula to in the next example.
A boat’s sail is in the shape of a right triangle as shown. The hypotenuse will be 17 feet long. The length of one side will be 7 feet less than the length of the other side. Find the lengths of the sides of the sail.
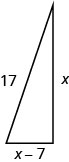
- Solution
-
Step 1. Read the problem Step 2. Identify what you are looking for. We are looking for the lengths of the
sides of the sail.Step 3. Name what you are looking for.
One side is 7 less than the other.Let x= length of a side of the sail.
x−7= length of other sideStep 4. Translate into an equation. Since this is a
right triangle we can use the Pythagorean Theorem.a2+b2=c2 Substitute in the variables. x2+(x−7)2=172 Step 5. Solve the equation
Simplify.x2+x2−14x+49=289 2x2−14x+49=289 It is a quadratic equation, so get zero on one side. 2x2−14x−240=0 Factor the greatest common factor. 2(x2−7x−120)=0 Factor the trinomial. 2(x−15)(x+8)=0 Use the Zero Product Property. 2≠0x−15=0x+8=0 Solve. 2≠0x=15x=−8 Since x is a side of the triangle, x=−8 does not
make sense.2≠0x=15x=−8 Find the length of the other side. If the length of one side is
then the length of the other side is


8 is the length of the other side.Step 6. Check the answer in the problem
Do these numbers make sense?
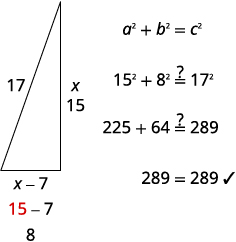
Step 7. Answer the question The sides of the sail are 8, 15 and 17 feet.
Justine wants to put a deck in the corner of her backyard in the shape of a right triangle. The length of one side of the deck is 7 feet more than the other side. The hypotenuse is 13. Find the lengths of the two sides of the deck.
- Answer
-
5 feet and 12 feet
A meditation garden is in the shape of a right triangle, with one leg 7 feet. The length of the hypotenuse is one more than the length of the other leg. Find the lengths of the hypotenuse and the other leg.
- Answer
-
24 feet and 25 feet
Access this online resource for additional instruction and practice with quadratic equations.
Key Concepts
- Polynomial Equation: A polynomial equation is an equation that contains a polynomial expression. The degree of the polynomial equation is the degree of the polynomial.
- Quadratic Equation: An equation of the form ax2+bx+c=0 is called a quadratic equation.
a,b,c are real numbers and a≠0
- Zero Product Property: If a·b=0, then either a=0 or b=0 or both.
- How to use the Zero Product Property
- Set each factor equal to zero.
- Solve the linear equations.
- Check.
- How to solve a quadratic equation by factoring.
- Write the quadratic equation in standard form, ax2+bx+c=0.
- Factor the quadratic expression.
- Use the Zero Product Property.
- Solve the linear equations.
- Check. Substitute each solution separately into the original equation.
- Zero of a Polynomial: For any polynomial f, if f(x)=0, then x is a zero of the polynomial.
- How to use a problem solving strategy to solve word problems.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
- Solve the equation using appropriate algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Practice Makes Perfect
Use the Zero Product Property
In the following exercises, solve.
1. (3a−10)(2a−7)=0
- Answer
-
a=103,a=72
2. (5b+1)(6b+1)=0
3. 6m(12m−5)=0
- Answer
-
m=0,m=512
4. 2x(6x−3)=0
5. (2x−1)2=0
- Answer
-
x=12
6. (3y+5)2=0
Solve Quadratic Equations by Factoring
In the following exercises, solve.
7. 5a2−26a=24
- Answer
-
a=−45,a=6
8. 4b2+7b=−3
9. 4m2=17m−15
- Answer
-
m=54,m=3
10. n2=5−6n
11. 7a2+14a=7a
- Answer
-
a=−1,a=0
12. 12b2−15b=−9b
13. 49m2=144
- Answer
-
m=127,m=−127
14. 625=x2
15. 16y2=81
- Answer
-
y=−94,y=94
16. 64p2=225
17. 121n2=36
- Answer
-
n=−611,n=611
18. 100y2=9
19. (x+6)(x−3)=−8
- Answer
-
x=2,x=−5
20. (p−5)(p+3)=−7
21. (2x+1)(x−3)=−4x
- Answer
-
x=32,x=−1
22. (y−3)(y+2)=4y
23. (3x−2)(x+4)=12x
- Answer
-
x=32,x=−1
24. (2y−3)(3y−1)=8y
25. 20x2−60x=−45
- Answer
-
x=−23
26. 3y2−18y=−27
27. 15x2−10x=40
- Answer
-
x=2,x=−43
28. 14y2−77y=−35
29. 18x2−9=−21x
- Answer
-
x=−32,x=13
30. 16y2+12=−32y
31. 16p3=24p2−9p
- Answer
-
p=0,p=34
32. m3−2m2=−m
33. 2x3+72x=24x2
- Answer
-
x=0, x=6
34. 3y3+48y=24y2
35. 36x3+24x2=−4x
- Answer
-
x=0, x=13
36. 2y3+2y2=12y
Solve Equations with Polynomial Functions
In the following exercises, solve.
37. For the function, f(x)=x2−8x+8, ⓐ find when f(x)=−4 ⓑ Use this information to find two points that lie on the graph of the function.
- Answer
-
ⓐ x=2 or x=6 ⓑ (2,−4) (6,−4)
38. For the function, f(x)=x2+11x+20, ⓐ find when f(x)=−8 ⓑ Use this information to find two points that lie on the graph of the function.
39. For the function, f(x)=8x2−18x+5, ⓐ find when f(x)=−4 ⓑ Use this information to find two points that lie on the graph of the function.
- Answer
-
ⓐ x=32 or x=34
ⓑ (32,−4) (34,−4)
40. For the function, f(x)=18x2+15x−10, ⓐ find when f(x)=15 ⓑ Use this information to find two points that lie on the graph of the function.
In the following exercises, for each function, find: ⓐ the zeros of the function ⓑ the x-intercepts of the graph of the function ⓒ the y-intercept of the graph of the function.
41. f(x)=9x2−4
- Answer
-
ⓐ x=23 or x=−23
ⓑ (23,0), (−23,0)
ⓒ (0,−4)
42. f(x)=25x2−49
43. f(x)=6x2−7x−5
- Answer
-
ⓐ x=53 or x=−12
ⓑ (53,0), (−12,0)
ⓒ (0,−5)
44. f(x)=12x2−11x+2
Solve Applications Modeled by Quadratic Equations
In the following exercises, solve.
45. The product of two consecutive odd integers is 143. Find the integers.
- Answer
-
−13, −11 and 11, 13
46. The product of two consecutive odd integers is 195. Find the integers.
47. The product of two consecutive even integers is 168. Find the integers.
- Answer
-
−14, −12 and 12, 14
48. The product of two consecutive even integers is 288. Find the integers.
49. The area of a rectangular carpet is 28 square feet. The length is three feet more than the width. Find the length and the width of the carpet.
- Answer
-
−4 and 7
50. A rectangular retaining wall has area 15 square feet. The height of the wall is two feet less than its length. Find the height and the length of the wall.
51. The area of a bulletin board is 55 square feet. The length is four feet less than three times the width. Find the length and the width of the a bulletin board.
- Answer
-
5, 11
52. A rectangular carport has area 150 square feet. The height of the carport is five feet less than twice its length. Find the height and the length of the carport.
53. A pennant is shaped like a right triangle, with hypotenuse 10 feet. The length of one side of the pennant is two feet longer than the length of the other side. Find the length of the two sides of the pennant.
- Answer
-
6, 8
54. A stained glass window is shaped like a right triangle. The hypotenuse is 15 feet. One leg is three more than the other. Find the lengths of the legs.
55. A reflecting pool is shaped like a right triangle, with one leg along the wall of a building. The hypotenuse is 9 feet longer than the side along the building. The third side is 7 feet longer than the side along the building. Find the lengths of all three sides of the reflecting pool.
- Answer
-
8, 15, 17
56. A goat enclosure is in the shape of a right triangle. One leg of the enclosure is built against the side of the barn. The other leg is 4 feet more than the leg against the barn. The hypotenuse is 8 feet more than the leg along the barn. Find the three sides of the goat enclosure.
57. Juli is going to launch a model rocket in her back yard. When she launches the rocket, the function h(t)=−16t2+32t models the height, h, of the rocket above the ground as a function of time, t. Find:
ⓐ the zeros of this function which tells us when the rocket will hit the ground. ⓑ the time the rocket will be 16 feet above the ground.
- Answer
-
ⓐ 0, 2 ⓑ 1
58. Gianna is going to throw a ball from the top floor of her middle school. When she throws the ball from 48 feet above the ground, the function h(t)=−16t2+32t+48 models the height, h, of the ball above the ground as a function of time, t. Find:
ⓐ the zeros of this function which tells us when the ball will hit the ground. ⓑ the time(s) the ball will be 48 feet above the ground. ⓒ the height the ball will be at t=1 seconds which is when the ball will be at its highest point.
Writing Exercises
59. Explain how you solve a quadratic equation. How many answers do you expect to get for a quadratic equation?
- Answer
-
Answers will vary.
60. Give an example of a quadratic equation that has a GCF and none of the solutions to the equation is zero.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next section? Why or why not?


