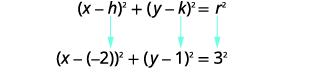8.2: Distance and Midpoint Formulas and Circles
- Page ID
- 66395
By the end of this section, you will be able to:
- Use the Distance Formula
- Use the Midpoint Formula
- Write the equation of a circle in standard form
- Graph a circle
Before you get started, take this readiness quiz.
- Find the length of the hypotenuse of a right triangle whose legs are \(12\) and \(16\) inches.
- Factor: \(x^{2}-18 x+81\).
- Solve by completing the square: \(x^{2}-12 x-12=0\).
Here we will discuss the next conic section: the circle. We need some preliminary discussions.
The Distance Formula
We have used the Pythagorean Theorem to find the lengths of the sides of a right triangle. Here we will use this theorem again to find distances on the rectangular coordinate system. By finding distance on the rectangular coordinate system, we can make a connection between the geometry of a conic and algebra—which opens up a world of opportunities for application.
Our first step is to develop a formula to find distances between points on the rectangular coordinate system. We will plot the points and create a right triangle much as we did when we found slope of a line. We then take it one step further and use the Pythagorean Theorem to find the length of the hypotenuse of the triangle—which is the distance between the points.
Use the rectangular coordinate system to find the distance between the points \((6,4)\) and \((2,1)\).
- Solution
-
Plot the two points. Connect the two points
with a line.
Draw a right triangle as if you were going to
find slope.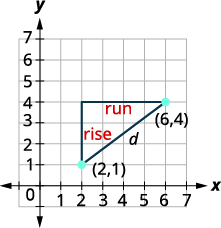
Find the length of each leg. 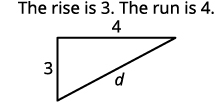
Use the Pythagorean Theorem to find \(d\), the distance between the two points. \(a^{2}+b^{2}=c^{2},\)
where \(c\) is the length of the hypotenuse (opposite the right angle) and \(a\) and \(b\) are the lengths of the other two sides.
Substitute in the values. \(3^{2}+4^{2}=d^{2}\) Simplify. \(9+16=d^{2}\) \(25=d^{2}\) Use the Square Root Property. \(d=5\quad\text{ or, }\cancel{d=-5}\) Since distance, \(d\) is positive, we can eliminate \(d=-5\). The distance between the points \((6,4)\) and \((2,1)\) is \(5\).
Use the rectangular coordinate system to find the distance between the points \((6,1)\) and \((2,-2)\).
- Answer
-
\(d=5\)
Use the rectangular coordinate system to find the distance between the points \((5,3)\) and \((-3,-3)\).
- Answer
-
\(d=10\)
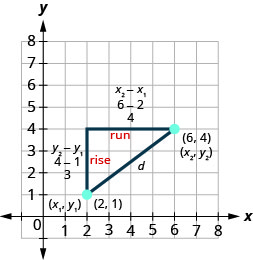
The method we used in the last example leads us to the formula to find the distance between the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\).
When we found the length of the horizontal leg we subtracted \(6−2\) which is \(x_{2}-x_{1}\).
When we found the length of the vertical leg we subtracted \(4−1\) which is \(y_{2}-y_{1}\).
If the triangle had been in a different position, we may have subtracted \(x_{1}-x_{2}\) or \(y_{1}-y_{2}\). The expressions \(x_{2}-x_{1}\) and \(x_{1}-x_{2}\) vary only in the sign of the resulting number. To get the positive value-since distance is positive- we can use absolute value. So to generalize we will say \(\left|x_{2}-x_{1}\right|\) and \(\left|y_{2}-y_{1}\right|\).
In the Pythagorean Theorem, we substitute the general expressions \(\left|x_{2}-x_{1}\right|\) and \(\left|y_{2}-y_{1}\right|\) rather than the numbers.
| \({a^{2}+b^{2}=c^{2}}\) | |
| Substitute in the values. | \({(|x_{2}-x_{1}|)^{2}+(|y_{2}-y_{1}|)^{2}=d^{2}}\) |
| Squaring the expressions makes them positive so eliminate the absolute value. | \({(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}}\) |
| Use the Square Root Property. | \(d=\pm\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\) |
| Distance is positive, so eliminate the negative solution. | \(d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\) |
This is the Distance Formula we use to find the distance \(d\) between the two points \((x_{1},y_{1})\) and \((x_{2}, y_{2})\).
The distance \(d\) between the two points \((x_{1},y_{1})\) and \((x_{2}, y_{2})\) is
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Use the Distance Formula to find the distance between the points \((-5,-3)\) and \((7,2)\).
- Solution
-
\((-5,-3)\) and \((7,2)\) Write the Distance Formula. \(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) Label the points.
\(\stackrel{(-5,-3)}{(x_1,y_1)}\quad\text{ and }\quad\stackrel{(7,2)}{(x_2,y_2)}\) Substitute. \(d=\sqrt{(7-(-5))^{2}+(2-(-3))^{2}}\)
Simplify. \(d=\sqrt{12^{2}+5^{2}}\)
\(d=\sqrt{144+25}\)
\(d=\sqrt{169}\)
\(d=13\)
Use the Distance Formula to find the distance between the points \((-4,-5)\) and \((5,7)\).
- Answer
-
\(d=15\)
Use the Distance Formula to find the distance between the points \((-2,-5)\) and \((-14,-10)\).
- Answer
-
\(d=13\)
Use the Distance Formula to find the distance between the points \((10,−4)\) and \((−1,5)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.
Solution
|
Write the Distance Formula. |
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) |
| Label the points, | \(\stackrel{(10,-4)}{(x_1,y_1)}\quad\text{ and }\stackrel{(-1,5)}{(x_2,y_2)}\) |
| and substitute. | \(d=\sqrt{(-1-10)^{2}+(5-(-4))^{2}}\) |
| Simplify. | \(d=\sqrt{(-11)^{2}+9^{2}}\) \(d=\sqrt{121+81}\) \(d=\sqrt{202}\) |
| Since \(202\) is not a perfect square, we can leave the answer in exact form or if we need to, we can find a decimal approximation. |
\(d=\sqrt{202}\), \(d \approx 14.2\) |
Use the Distance Formula to find the distance between the points \((−4,−5)\) and \((3,4)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.
- Answer
-
\(d=\sqrt{130}, d \approx 11.4\)
Use the Distance Formula to find the distance between the points \((−2,−5)\) and \((−3,−4)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.
- Answer
-
\(d=\sqrt{2}, d \approx 1.4\)
Use the Midpoint Formula
It is often useful to be able to find the midpoint of a segment, i.e., the point that divides a segment in half. For example, if you have the endpoints of the diameter of a circle, you may want to find the center of the circle which is the midpoint of the diameter. To find the midpoint of a line segment, we find the average of the \(x\)-coordinates and the average of the \(y\)-coordinates of the endpoints. To see why this is the case, consider two points, \(P\) and \(Q\), together with the midpoint \(M\) of the segment \(PQ\) and the triangle formed below:
1.png?revision=2&size=bestfit&width=350&height=350)
The triangle \(\triangle PQS\) is similar to the triangle \(\triangle PMR\) because \(\angle PRM\) and \(\angle PSQ\) both right triangles and the two triangles share the angle \(P\). Since \(M\) is the midpoint the length of \(PQ\), \(|PQ|\), is twice the length of \(PM\), \(|PM|\), i.e.,
\[|PM|=\dfrac12\cdot |PQ|.\]
When two triangles are similar, the ratios of corresponding sides are equal. So,
\[\dfrac{|PR|}{|PS|}=\dfrac{|PM|}{|PQ|}=\dfrac{|PQ|}{2|PQ|}=\dfrac12.\]
So, we see that \[|PR|=\dfrac12\cdot|PS|.\]
We see then that \(R\) is the midpoint of \(PS\), and since the segment is vertical we can calculate the \(y\)-coordinate of the midpoint \(R\) by calculating the average of the \(y\) coordinates of \(P\) and \(S\). But the \(y\)-coordinates of \(P, M, and Q\) are the \(y\)-coordinates of \(P,R,\) and \(S\), respectively, so we can calculate the \(y\)-coordinate of \(M\) by calculating the average of the \(y\) coordinates of \(P\) and \(Q\). A similar story unfolds for the \(x\) coordinates.
The midpoint of the line segment whose endpoints are the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\) is
\(\left(\dfrac{x_{1}+x_{2}}{2}, \dfrac{y_{1}+y_{2}}{2}\right)\)
To find the midpoint of a line segment, we find the average of the \(x\)-coordinates and the average of the \(y\)-coordinates of the endpoints.
Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−5,−4)\) and \((7,2)\). Plot the endpoints and the midpoint on a rectangular coordinate system.
Solution:
| Write the Midpoint Formula. | \(\left(\dfrac{x_{1}+x_{2}}{2}, \dfrac{y_{1}+y_{2}}{2}\right)\) |
| Label the points, | \(\stackrel{(-5,-4)}{(x_1,y_1)}\quad\text{ and }\quad\stackrel{(7,2)}{(x_2,y_2)}\) |
| and substitute. | \(\left(\dfrac{-5+7}{2}, \dfrac{-4+2}{2}\right)\) |
| Simplify. | \(\left(\dfrac{2}{2}, \dfrac{-2}{2}\right)\) |
|
\((1,-1)\) The midpoint of the segment is the point \((1,-1)\). |
|
| Plot the endpoints and midpoint. |
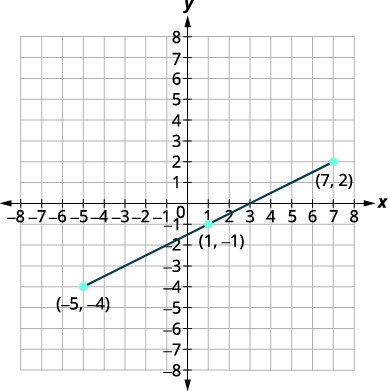
|
Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−3,−5)\) and \((5,7)\). Plot the endpoints and the midpoint on a rectangular coordinate system.
- Answer
-
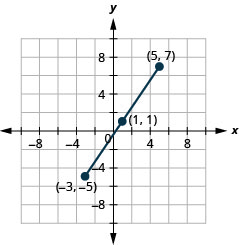
Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−2,−5)\) and \((6,−1)\). Plot the endpoints and the midpoint on a rectangular coordinate system.
- Answer
-
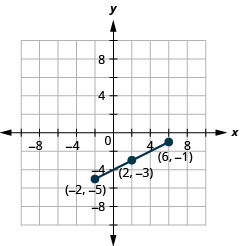
Both the Distance Formula and the Midpoint Formula depend on two points, \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\). It is easy to confuse which formula requires addition and which subtraction of the coordinates. If we remember where the formulas come from, is may be easier to remember the formulas.
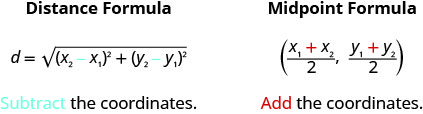
Finding the Perpendicular Bisector of a Line Segment
The Perpendicular Bisector of a line segment \(PQ\) is the line that is perpendicular to \(PQ\) and passes through though the midpoint of \(PQ\).
Find the perpendicular bisector of the line segment whose endpoints are \(5,8\) and \(9,2\).
Solution
A line is determined by a point on the line (in this case the midpoint of the given segment) and the slope.
|
The perpendicular bisector passes through the midpoint of the given line segment. So we must calculate the midpoint by averaging the \(x\)-coordinates, and averaging the \(y\)-coordinates. |
\(M=\left(\dfrac{5+9}{2},\dfrac{8+2}{2}\right)\) |
| Simplify. | \(M=(7,5)\) |
| We now need to find the slope of the line. To do this, we first find the slope of the given segment. | \(m_{\text{segment}}=\dfrac{2-8}{9-5}=\dfrac{-6}{4}=-\dfrac32\) |
| The slope of a line perpendicular to this segment has a slope that is the negative reciprocal of the slope of this segment. We calculate the slope of the desired line. | \(m_{\text{p.b.}}=-\dfrac{1}{m_{\text{segment}}}=-\dfrac{1}{-\dfrac32}=\dfrac{2}{3}\) |
| Use the slope obtained together with the midpoint to find an equation of the perpendicular bisector. |
\(M=(7,5), \quad m=\dfrac23\) \(y-5=\dfrac23 (x-7)\) |
| If desired, write in standard form (or any desired form). |
\(3(y-5)=2(x-7)\) \(3y-15=2x-14\) \(2x-3y=-1\) |
|
We could check our answer by graphing which will help to detect major errors. |
The line appears to be perpendicular to the line segment and also pass through the midpoint of the line segment. |
Find the perpendicular bisector of the line segment connecting the points \((-3,5)\) and \((5,-7)\).
- Answer
-
\(y+1=\dfrac23(x-1)\)
or
\(2x-3y=5\)
Find the perpendicular bisector of the line segment connecting the points \(\left(-2,\dfrac72\right)\) and \(\left(-5,-\dfrac52\right)\).
- Answer
-
\(y-\dfrac{1}{2}=-\dfrac12\left(x+\dfrac72\right)\)
Write the Equation of a Circle in Standard Form
As we mentioned, our goal is to connect the geometry of a conic with algebra. By using the coordinate plane, we are able to do this easily.
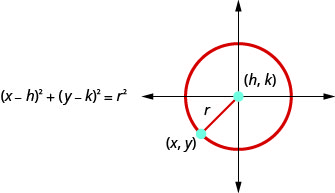
We define a circle as all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center, \((h,k)\), and the fixed distance is called the radius, \(r\), of the circle.
A circle is all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center, \((h,k)\), and the fixed distance is called the radius, \(r\), of the circle.
We look at a circle in the rectangular coordinate system. The radius is the distance from the center, \((h,k)\),to a point on the circle, \((x,y)\). |
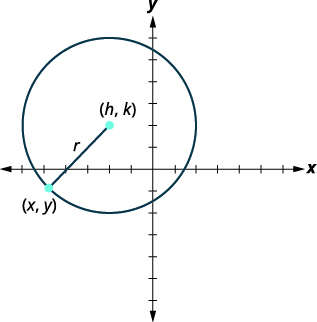
|
| To derive the equation of a circle, we can use the distance formula with the points \((h,k)\), \((x,y)\) and the distance, \(r\). |
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) |
| Substitute the values. | \(r=\sqrt{(x-h)^{2}+(y-k)^{2}}\) |
| Square both sides. | \(r^{2}=(x-h)^{2}+(y-k)^{2}\) |
This is the standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\).
The standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\), is
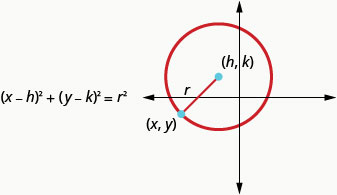
Write the standard form of the equation of the circle with radius \(3\) and center \((0,0)\).
Solution:
| Use the standard form of the equation of a circle. | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
|
Identify the center and radius. |
\(\stackrel{(0,0)}{(h,k)}\text{ and }\stackrel{3}{r}\) |
| Substitute in the values \(r=3, h=0\), and \(k=0\). | \((x-0)^{2}+(y-0)^{2}=3^{2}\) |
| Simplify. | \(x^{2}+y^{2}=9\) |
Write the standard form of the equation of the circle with a radius of \(6\) and center \((0,0)\).
- Answer
-
\(x^{2}+y^{2}=36\)
Write the standard form of the equation of the circle with a radius of \(8\) and center \((0,0)\).
- Answer
-
\(x^{2}+y^{2}=64\)
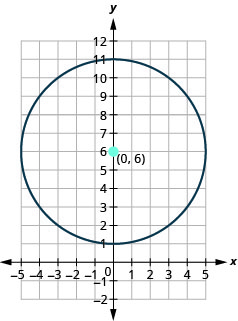
In the last example, the center was \((0,0)\). Notice what happened to the equation. Whenever the center is \((0,0)\), the standard form becomes \(x^{2}+y^{2}=r^{2}\).
Write the standard form of the equation of the circle with radius \(2\) and center \((−1,3)\).
Solution:
| Use the standard form of the equation of a circle. | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
|
Identify the center and radius. |
\(\stackrel{(-1,3)}{(h,k)}\text{ and }\stackrel{2}{r}\) |
| Substitute in the values. | \((x-(-1))^{2}+(y-3)^{2}=2^{2}\) |
| Simplify. | \((x+1)^{2}+(y-3)^{2}=4\) |
Write the standard form of the equation of the circle with a radius of \(7\) and center \((2,−4)\).
- Answer
-
\((x-2)^{2}+(y+4)^{2}=49\)
Write the standard form of the equation of the circle with a radius of \(9\) and center \((−3,−5)\).
- Answer
-
\((x+3)^{2}+(y+5)^{2}=81\)
In the next example, the radius is not given. To calculate the radius, we use the Distance Formula with the two given points.
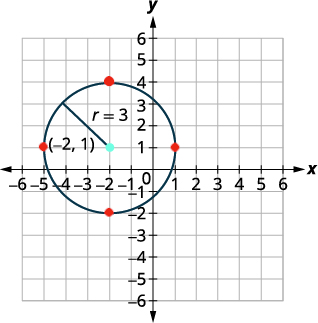
Write the standard form of the equation of the circle with center \((2,4)\) that also contains the point \((−2,1)\).
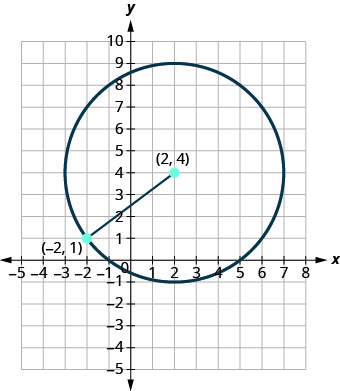
Solution:
|
The radius is the distance from the center to any point on the circle so we can use the distance formula to calculate it. We will use the center \((2,4)\) and point \((−2,1)\) Use the Distance Formula to find the radius. |
\(r=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) |
| Label the points, | \(\stackrel{(2,4)}{(x_{1}, y_{1})}\text{ and }\stackrel{(-2,1)}{(x_{2}, y_{2})}\) |
| and substitute the values to find \(r\). | \(r=\sqrt{(-2-2)^{2}+(1-4)^{2}}\) |
| Simplify. |
\(r=\sqrt{(-4)^{2}+(-3)^{2}}\) |
| Now that we know the radius, \(r=5\), and the center, \((2,4)\), we can use the standard form of the equation of a circle to find the equation. | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
|
Substitute in the values. |
\((x-2)^{2}+(y-4)^{2}=5^{2}\) |
| Simplify. | \((x-2)^{2}+(y-4)^{2}=25\) |
Write the standard form of the equation of the circle with center \((2,1)\) that also contains the point \((−2,−2)\).
- Answer
-
\((x-2)^{2}+(y-1)^{2}=25\)
Write the standard form of the equation of the circle with center \((7,1)\) that also contains the point \((−1,−5)\).
- Answer
-
\((x-7)^{2}+(y-1)^{2}=100\)
Graph a Circle
Any equation of the form \((x-h)^{2}+(y-k)^{2}=r^{2}\) is the standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\). We can then graph the circle on a rectangular coordinate system.
Note that the standard form calls for subtraction from \(x\) and \(y\). In the next example, the equation has \(x+2\), so we need to rewrite the addition as subtraction of a negative.
Find the center and radius, then graph the circle: \((x+2)^{2}+(y-1)^{2}=9\).
Solution:
|
\((x+2)^{2}+(y-1)^{2}=9\) |
|
|
Use the standard form of the equation of a circle. Identify the center, \((h,k)\) and radius, \(r\). |
\((x-h)^2+(y-k)^2=r^2\) \((x-(-2))^2+(y-1)^2=3^2\) |
| Center: \((-2,1)\) radius: \(3\) | |
| Use four points (N,S,E, and W of center) to guide the sketch by adding and subtracting the radius to the \(y\)-coordinate and the \(x\)-coordinate in turn. |
Center: \((-2,1)\) \((-2,1+3)=(-2,4)\) \((-2,1-3)=(-2,-2)\) \((-2+3,1)=(1,1)\) \((-2-3,1)=(-5,1)\) |
| Graph the circle. |
|
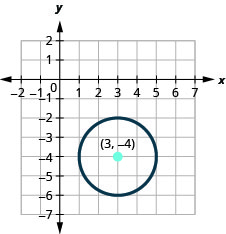
- Find the center and radius, then
- Find the 4 points N, S, E, and W of the center. Graph the circle: \((x-3)^{2}+(y+4)^{2}=4\).
- Answer
-
- The circle is centered at \((3,-4)\) with a radius of \(2\).
- \((3,-2), (3,-6), (5,-4), (1,-4)\)
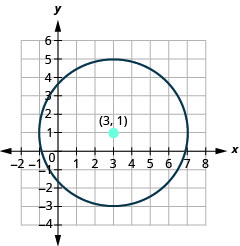
- Find the center and radius, then
- Find the four points N, S, E, and W of center. Graph the circle: \((x-3)^{2}+(y-1)^{2}=16\).
- Answer
-
- The circle is centered at \((3,1)\) with a radius of \(4\).
- \((3,5), (3,-3), (7,1), (-1,1)\)
If we expand the equation from Example 11.24, we see a different form:
| \((x+2)^{2}+(y-1)^{2}=9\) | |
|
Square the binomials. |
\(x^2+4x+4+y^2-2y+1=9\) |
|
Arrange the terms in descending degree order, and get zero on the right |
\(x^2+y^2+4x-2y-4=0.\) |
This form of the equation is called the general form of the equation of the circle.
The general form of the equation of a circle is
\(x^{2}+y^{2}+a x+b y+c=0\)
If we are given an equation in general form, we can change it to standard form by completing the squares in both \(x\) and \(y\). Then we can graph the circle using its center and radius.
- Find the center and radius, then
- Graph the circle: \(x^{2}+y^{2}-4 x-6 y+4=0\)
Solution:
We need to rewrite this general form into standard form in order to find the center and radius.
|
|
||
| Group the \(x\)-terms and \(y\)-terms. Collect the constants on the right side. |
\(x^{2}-4x+y^{2}-6 y=-4\) | |
| Complete the squares. |
|
|
| Rewrite as binomial squares. |
|
|
| Identify the center and radius. | Center: \((2,3)\) radius: \(3\) | |
| Identify four points on the circle to guide the sketch. | \((2,6),(2,0),(5,3),(-1,3)\) | |
| Graph the circle. |
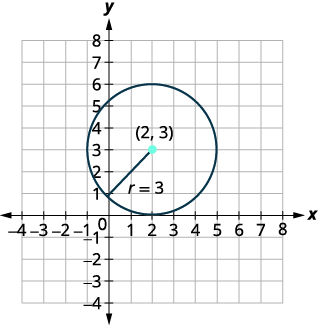
|
- Find the center and radius, then
- Identify four points to guide the sketch of the graph. Graph the circle: \(x^{2}+y^{2}-6 x-8 y+9=0\).
- Answer
-
- The circle is centered at \((3,4)\) with a radius of \(4\).
- \((3,8),(3,0), (7,4),(-1,4)\)
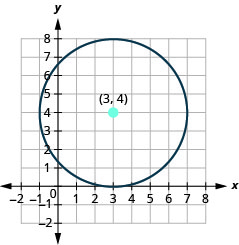
- Find the center and radius, then
- Graph the circle: \(x^{2}+y^{2}+6 x-2 y+1=0\)
- Answer
-
- The circle is centered at \((-3,1)\) with a radius of \(3\).
- \((-3,4),(-3,-2), (0,1), (-6,1)\)
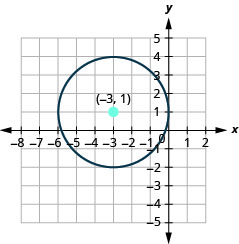
In the next example, there is a \(y\)-term and a \(y^{2}\)-term. But notice that there is no \(x\)-term, only an \(x^{2}\)-term. We have seen this before and know that it means \(h\) is \(0\). We will need to complete the square for the \(y\) terms, but not for the \(x\) terms.
- Find the center and radius, then
- Graph the circle: \(x^{2}+y^{2}+8 y=0\)
Solution:
We need to rewrite this general form into standard form in order to find the center and radius.
| \(x^{2}+y^{2}+8 y=0\) | |
| Group the \(x\)-terms and \(y\)-terms. | \(x^2+y^2+8y=0\) |
| There are no constants to collect on the right side. | |
| Complete the square for \(y^{2}+8y\). |
\(x^2+y^2+8y+16-16=0\) \(x^2+y^2+8y+16=16\) |
| Rewrite as binomial squares. | \((x-0)^2+(y+4)^2=16\) |
| Identify the center and radius. | Center: \((0,-4)\) radius: \(4\) |
| Identify four points to guide our sketch. | \((0,0), (0,-16),(4,0),(-4,0)\) |
| Graph the circle. | 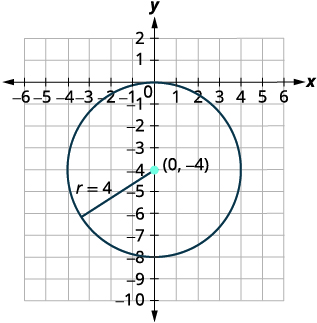 |
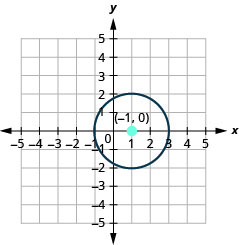
- Find the center and radius, then
- Graph the circle: \(x^{2}+y^{2}-2 x-3=0\).
- Answer
-
- The circle is centered at \((-1,0)\) with a radius of \(2\).
- \((-1,2),(-1,-2),(1,0),(-3,0)\)
- Find the center and radius, then
- Graph the circle: \(x^{2}+y^{2}-12 y+11=0\).
- Answer
-
- The circle is centered at \((0,6)\) with a radius of \(5\).
- \((0,11), (0,1), (5,6), (-5,6)\)
Key Concepts
- Distance Formula: The distance \(d\) between the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\) is
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
- Midpoint Formula: The midpoint of the line segment whose endpoints are the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\) is
\(\left(\dfrac{x_{1}+x_{2}}{2}, \dfrac{y_{1}+y_{2}}{2}\right)\)
To find the midpoint of a line segment, we find the average of the \(x\)-coordinates and the average of the \(y\)-coordinates of the endpoints. - Circle: A circle is all points in a plane that are a fixed distance from a fixed point in the plane. The given point is called the center, \((h,k)\), and the fixed distance is called the radius, \(r\), of the circle.
- Standard Form of the Equation a Circle: The standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\), is
- General Form of the Equation of a Circle: The general form of the equation of a circle is
\(x^{2}+y^{2}+a x+b y+c=0\)
Glossary
- circle
- A circle is all points in a plane that are a fixed distance from a fixed point in the plane.
Practice Makes Perfect
In the following exercises, find the distance between the points. Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.
- \((2,0)\) and \((5,4)\)
- \((-4,-3)\) and \((2,5)\)
- \((-4,-3)\) and \((8,2)\)
- \((-7,-3)\) and \((8,5)\)
- \((-1,4)\) and \((2,0)\)
- \((-1,3)\) and \((5,-5)\)
- \((1,-4)\) and \((6,8)\)
- \((-8,-2)\) and \((7,6)\)
- \((-3,-5)\) and \((0,1)\)
- \((-1,-2)\) and \((-3,4)\)
- \((3,-1)\) and \((1,7)\)
- \((-4,-5)\) and \((7,4)\)
- Answer
-
1. \(d=5\)
3. \(13\)
5. \(5\)
7. \(13\)
9. \(d=3 \sqrt{5}, d \approx 6.7\)
11. \(d=\sqrt{68}, d \approx 8.2\)
In the following exercises,
- find the midpoint of the line segments whose endpoints are given and
- plot the endpoints and the midpoint on a rectangular coordinate system.
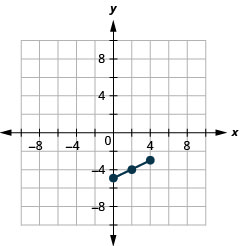
- \((0,-5)\) and \((4,-3)\)
- \((-2,-6)\) and \((6,-2)\)
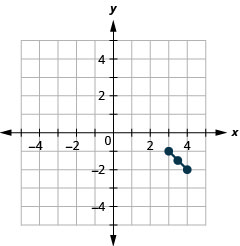
- \((3,-1)\) and \((4,-2)\)
- \((-3,-3)\) and \((6,-1)\)
- Answer
-
13.
- Midpoint: \((2,-4)\)
15.
- Midpoint: \(\left(3 \dfrac{1}{2},-1 \dfrac{1}{2}\right)\)
17. \((-9,9), (25, -25)\)
18. \((0.02, -3.5), (1.06,-11.7)\)
In the following exercises, write the standard form of the equation of the circle with the given radius and center \((0,0)\).
- Radius: \(7\)
- Radius: \(9\)
- Radius: \(\sqrt{2}\)
- Radius: \(\sqrt{5}\)
- Answer
-
19. \(x^{2}+y^{2}=49\)
21. \(x^{2}+y^{2}=2\)
In the following exercises, write the standard form of the equation of the circle with the given radius and center
- Radius: \(1\), center: \((3,5)\)
- Radius: \(10\), center: \((-2,6)\)
- Radius: \(2.5\), center: \((1.5, -3.5)\)
- Radius: \(1.5\), center: \((-5.5, -6.5)\)
- Answer
-
23. \((x-3)^{2}+(y-5)^{2}=1\)
25. \((x-1.5)^{2}+(y+3.5)^{2}=6.25\)
For the following exercises, write the standard form of the equation of the circle with the given center with point on the circle.
- Center \((3,−2)\) with point \((3,6)\)
- Center \((6,−6)\) with point \((2,−3)\)
- Center \((4,4)\) with point \((2,2)\)
- Center \((−5,6)\) with point \((−2,3)\)
- Answer
-
27. \((x-3)^{2}+(y+2)^{2}=64\)
29. \((x-4)^{2}+(y-4)^{2}=8\)
In the following exercises,
- find the center and radius, then
- graph each circle.
- \((x+5)^{2}+(y+3)^{2}=1\)
- \((x-2)^{2}+(y-3)^{2}=9\)
- \((x-4)^{2}+(y+2)^{2}=16\)
- \((x+2)^{2}+(y-5)^{2}=4\)
- \(x^{2}+(y+2)^{2}=25\)
- \((x-1)^{2}+y^{2}=36\)
- \((x-1.5)^{2}+(y+2.5)^{2}=0.25\)
- \((x-1)^{2}+(y-3)^{2}=\dfrac{9}{4}\)
- \(x^{2}+y^{2}=64\)
- \(x^{2}+y^{2}=49\)
- Answer
-
31.
- The circle is centered at \((−5,−3)\) with a radius of \(1\).
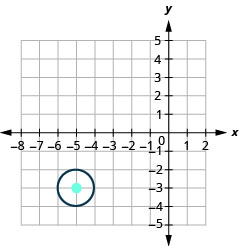
33.
- The circle is centered at \((4,−2)\) with a radius of \(4\).
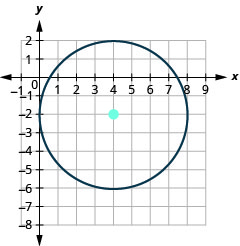
35.
- The circle is centered at \((0,−2)\) with a radius of \(5\).
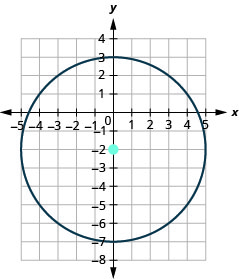
37.
- The circle is centered at \((1.5,2.5)\) with a radius of \(0.5\).
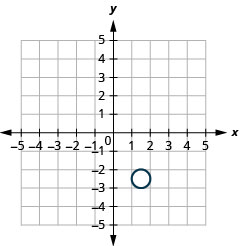
39.
- The circle is centered at \((0,0)\) with a radius of \(8\).
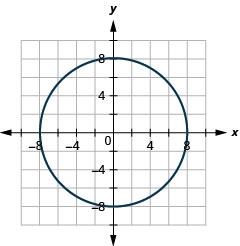
In the following exercises,
- identify the center and radius and
- graph.
- \(x^{2}+y^{2}+2 x+6 y+9=0\)
- \(x^{2}+y^{2}-6 x-8 y=0\)
- \(x^{2}+y^{2}-4 x+10 y-7=0\)
- \(x^{2}+y^{2}+12 x-14 y+21=0\)
- \(x^{2}+y^{2}+6 y+5=0\)
- \(x^{2}+y^{2}-10 y=0\)
- \(x^{2}+y^{2}+4 x=0\)
- \(x^{2}+y^{2}-14 x+13=0\)
- Answer
-
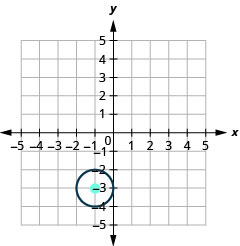
41.
- Center: \((−1,−3)\), radius: \(1\)
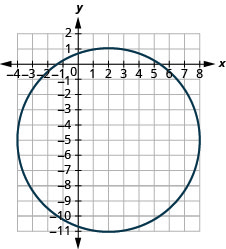
43.
- Center: \((2,−5)\), radius: \(6\)
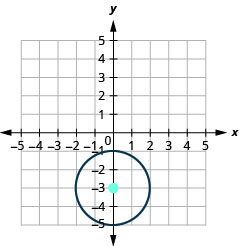
45.
- Center: \((0,−3)\), radius: \(2\)
47.
- Center: \((−2,0)\), radius: \(-2\)
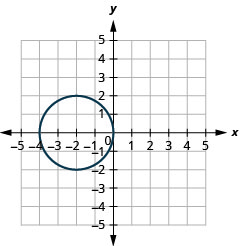
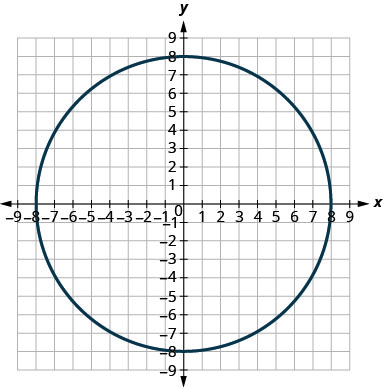
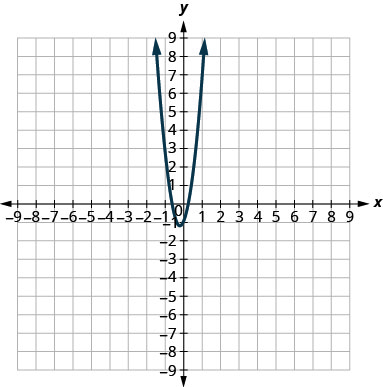
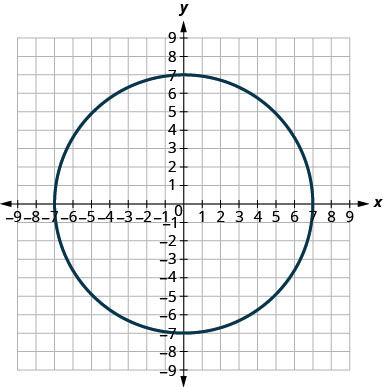
In the following exercises, match each graph to one of the following equations:
- \(x^{2}+y^{2}=64\)
- \(x^{2}+y^{2}=49\)
- \((x+5)^{2}+(y+2)^{2}=4\)
- \((x-2)^{2}+(y-3)^{2}=9\)
- \(y=-x^{2}+8 x-15\)
- \(y=6 x^{2}+2 x-1\)
49.
50.
51.
52.
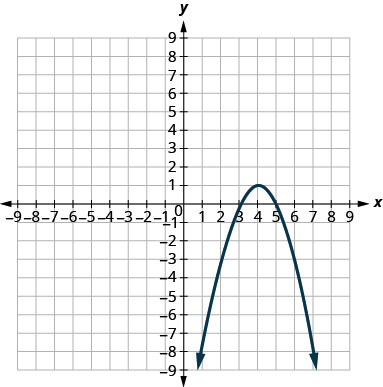
53.
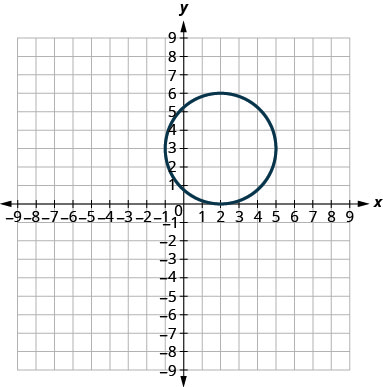
54.
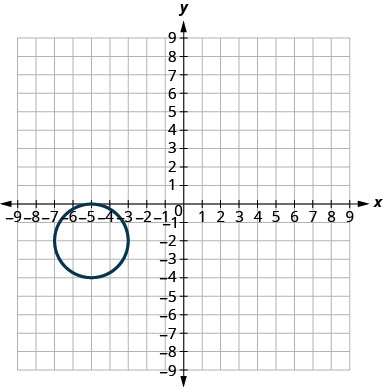
- Answer
-
49. a
51. b
53. d
- Explain the relationship between the distance formula and the equation of a circle.
- Is a circle a function? Explain why or why not.
- In your own words, state the definition of a circle.
- In your own words, explain the steps you would take to change the general form of the equation of a circle to the standard form.
- Answer
-
53. Answers will vary.
55. Answers will vary.
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.



1.png?revision=1&size=bestfit&width=171&height=161)