Section 3.1: Absolute Value

Last updated
Save as PDF

Page ID: 192820

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Be Prepared

We will rely heavily on these skills throughout this section.

Simplify: a. $|-7|$ and b. $|-3+2|-1$
Plot the points $(-3,3)$ and $(2,2)$ on graph paper
Simplify: $-(2-3x) - (x-4)$

Learning Objectives

Motivating Problem

You’re standing at a subway station at position 0. A friend is at -5, and another friend is at +7. Who’s farther from you? Does direction matter if you’re only interested in distance?

Fun Fact

Karl Weierstrass first introduced the absolute value symbol $|x|$ in the 1800s as a means to formalize the concept of distance from zero, an idea that is widely used in science, finance, and navigation.

The Goal

In this section, we’ll learn what absolute value means and how to represent it on a number line and a coordinate plane. We’ll explore symmetry and how absolute value reflects distance, regardless of direction.

Absolute Value

In a sense, the absolute value of a number is a measure of its magnitude, its distance from zero, without its sign. Thus,

\[|7|=7 \qquad \text { and } \qquad |-7| =7 \nonumber \]

Here is the formal definition of the absolute value of a real number.

Definition: Absolute Value

To find the absolute value of any real number, first locate the number on the real line.

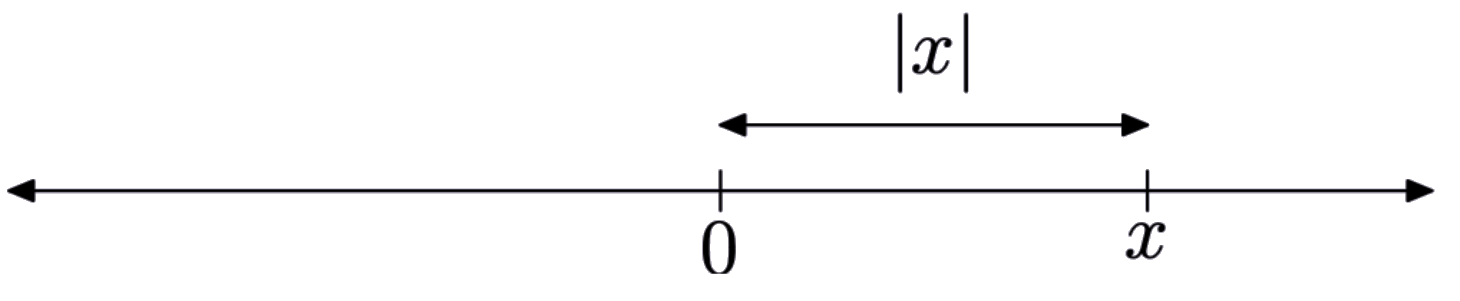
$WeChatfe21ab7cdaad1f1de591d514b27d3961.png$

The absolute value of the number is defined as its distance from the origin.

For example, to find the absolute value of 7, locate 7 on the real line and then find its distance from the origin.

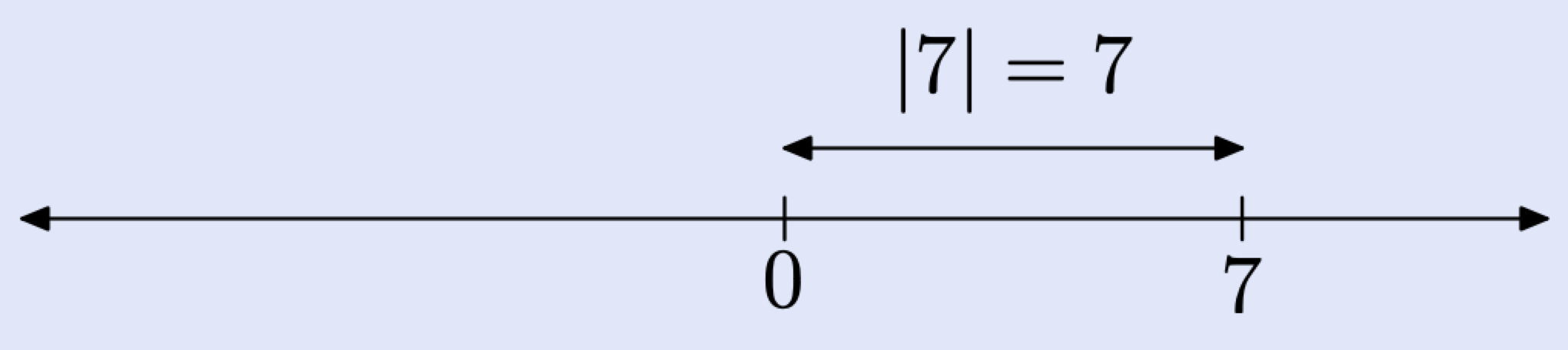
$WeChata761aa5433a8c3d11266fd5abcd2913b.png$

To find the absolute value of -7, locate -7 on the real line and then find its distance from the origin.

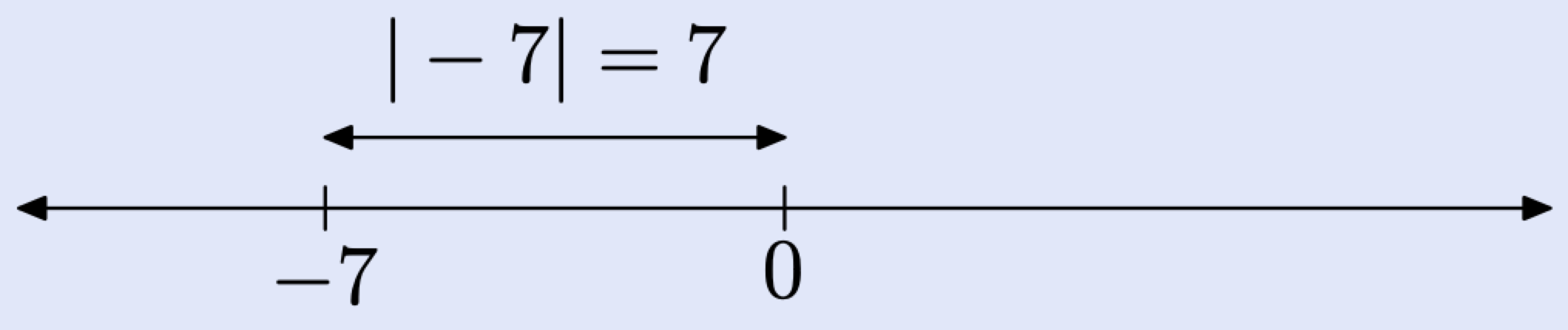
$WeChatc39901c112b7c3e585128057661b2373.png$

Some like to say that taking the absolute value “produces a number that is always positive.” However, this ignores an important exception, that is,

\[|0|=0 \nonumber \]

When we take the absolute value of a number, the result is always nonnegative; that is, the result is either positive or zero. In symbols,

\[|x| \geq 0 \text { for all real numbers } x \nonumber \]

This makes sense when we think of the $|x|$ as the distance from $x$ to zero, since distance is always nonnegative.

However, the discussion above is not of sufficient depth to handle more sophisticated problems involving absolute value.

A Piecewise Definition of Absolute Value

Because absolute value is intimately connected with distance, mathematicians and scientists find it an invaluable tool for measurement and error analysis. However, we will need a formulaic definition of the absolute value if we want to use this tool effectively. We need to develop a piecewise definition of the absolute value function that defines the absolute value for any arbitrary real number $x$.

We begin with a few observations. Remember, the absolute value of a number is always nonnegative (positive or zero).

If a number is negative, negating that number will make it positive. $|-5|=-(-5)=5$, and similarly, $|-12|=-(-12)=12$. Thus, if $x<0$ (if $x$ is negative), then $|x|=-(x)$.
If $x=0$, then $|x|=0$.
If a number is positive, taking the absolute value of that number does not change anything.

\[|5|=5, \text { and similarly, }|12|=12 \nonumber \]

Thus, if $x>0$ (if $x$ is positive), then $|x|=x$.

We can summarize these three cases with a piecewise definition.

\[|x|=\left\{\begin{array}{ll}{-x,} & {\text { if } x<0} \\ {0,} & {\text { if } x=0} \\ {x,} & {\text { if } x>0}\end{array}\right. \nonumber \]

It is the first line in our piecewise definition that usually leaves students scratching their heads. They might say, “I thought absolute value makes a number positive (or zero), yet you have $|x| = -x$; that is, you have the absolute value of $x$ equal to a negative $x$.” Try as they might, this seems contradictory. Does it seem so to you?

However, there is no contradiction. If $x<0$, that is, if $x$ is a negative number, then $-x$ is a positive number. For example, if $x=-8$, then $-x=8$, and even though we say “negative $x$,” in this case, $-x$ is a positive number.

If this still has you running confused, consider the simple fact that $x$ and $-x$ must have “opposite signs.” If one is positive, the other is negative, and vice versa. Consequently,

if $x$ is positive, then $-x$ is negative, but
if $x$ is negative, then $-x$ is positive.

Let’s summarize what we’ve learned thus far.

Summarizing the Definition on a Number Line

We like to use a number line to help summarize the definition of the absolute value of x.

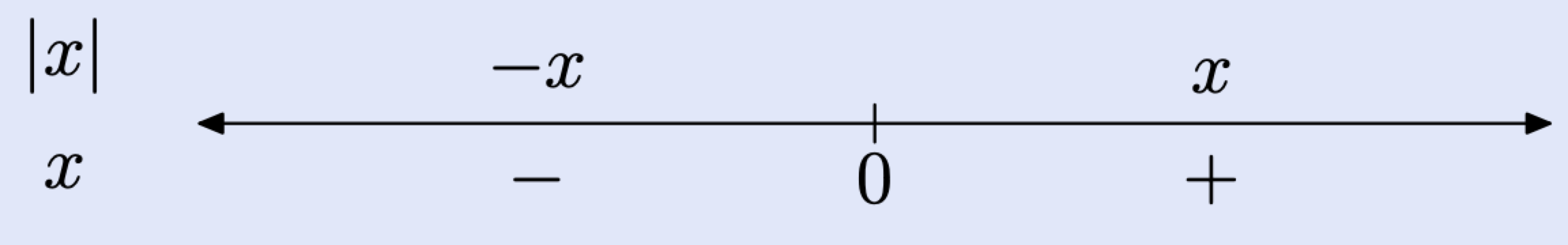
$WeChatd6ba895737ff52a6a145279fafa8da67.png$

Some remarks are in order for this summary on the number line.

We first draw the real line, then mark the “critical value” for the expression inside the absolute value bars on the number line. The number zero is a critical value for the expression x, because $x$ changes sign as you move from one side of zero to the other.
To the left of zero, $x$ is a negative number. We indicate this with the minus sign below the number line. To the right of zero, $x$ is a positive number, indicated with a plus sign below the number line.
Above the number line, we simplify the expression $|x|$. To the left of zero, $x$ is a negative number (look below the line), so $|x|=-x$. Note how the result $-x$ is placed above the line to the left of zero. Similarly, to the right of zero, $x$ is a positive number (look below the line), so $|x|=x$. Note how the result $x$ is placed above the line to the right of zero.

In the piecewise definition of $|x|$, we have three distinct pieces, one for each of the cases discussed above. However, because $|0|=0$, we can include this case with the piece $|x|=x$, if we adjust the condition to include zero.

Definition

\[|x|=\left\{\begin{array}{ll}{-x,} & {\text { if } x<0} \\ {x,} & {\text { if } x\geq 0}\end{array}\right. \nonumber \]

Note that this piecewise definition agrees with our discussion to date.

If $x$ is a negative number (i.e., if $x < 0$), then the absolute value must change $x$ to a positive number by negating. That is, $|x|=-x$.
If $x$ is positive or zero (i.e., if $x \geq 0$), then there’s nothing to do except remove the absolute value bars. That is, $|x|=x$.

Constructing Piecewise Definitions

Let’s see if we can determine piecewise definitions for other expressions involving absolute value.

Example 1

Determine a piecewise definition for $|x-2|$.

Solution

First, find the "critical value" of the expression, the point at which the expression within the absolute value bars will change sign. This occurs when $x-2=0$.

\[\begin{aligned} x-2 &=0 \\ x &=2 \end{aligned} \nonumber \]

Draw a real line and mark this critical value of $x$ on the line. Place the expression $x-2$ below the line at its left end.

$WeChatcde0f7a6577ffaa8ef9bef52276b8462.png$

Next, determine the sign of $x-2$ for values of $x$ on each side of 2. This is easily done by “testing” a point on each side of 2 in the expression $x-2$.

Take $x=1$, which lies to the left of the critical value 2 on our number line. Substitute this value of $x$ in the expression $x-2$, obtaining

\[x-2=1-2=-1 \nonumber \]

which is negative. Indeed, regardless of which x-value you pick to the left of 2, when inserted into the expression $x-2$, you will get a negative result (you should check this for other values of $x$ to the left of 2). We indicate that the expression $x-2$ is negative for values of $x$ to the left of 2 by placing a minus (-) sign below the number line to the left of 2.

Next, pick $x=3$, which lies to the right of the critical value 2 on the number line. Substitute this value of $x$ into the expression $x-2$, obtaining

\[x-2=3-2=1 \nonumber \]

which is positive. Indeed, regardless of which x-value you pick to the right of 2, when inserted into the expression $x-2$, you will get a positive result (you should check this for other values of $x$ to the right of 2). We indicate that the expression $x-2$ is positive for values of $x$ to the right of 2 by placing a plus (+) sign below the number line to the right of 2.

$WeChata4b5e37ed22bde976a06d30e0de4c72e.png$

The next step is to remove the absolute value bars from the expression $|x-2|$, depending on the sign of $x-2$.

To the left of 2, the expression $x-2$ is negative (note the minus sign (-) below the number line), so $|x-2|=-(x-2)$. That is, we have to negate $x-2$ to make it positive. This is indicated by placing $-(x-2)$ above the line to the left of 2.

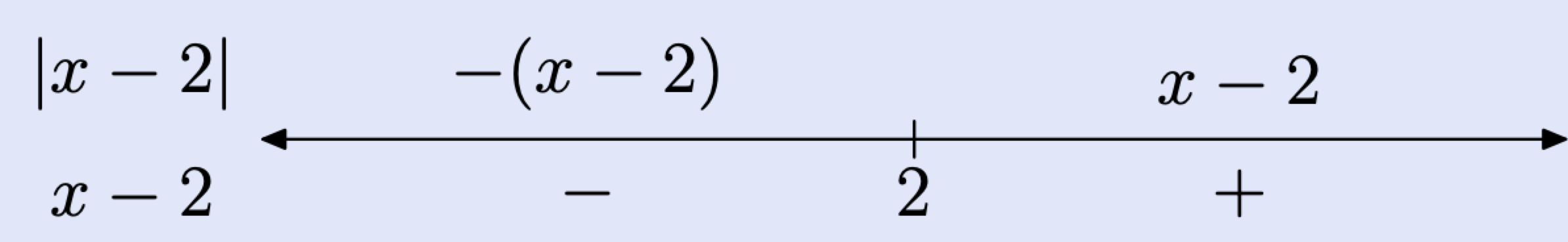
$WeChat5d2a2507db05ef85ac6bd6f581abc31d.png$

To the right of 2, the expression $x-2$ is positive (note the plus sign (+) below the line), so $|x-2|=x-2$. That is, we simply remove the absolute value bars because the quantity inside is already positive. This is indicated by placing $x-2$ above the line to the right of 2 (see the number line above).

We can use this last number line summary to construct a piecewise definition of the expression $|x-2|$.

\[|x-2|=\left\{\begin{array}{ll}{-(x-2),} & {\text { if } x<2,} \\ {x-2,} & {\text { if } x \geq 2}\end{array}=\left\{\begin{array}{ll}{-x+2,} & {\text { if } x<2} \\ {x-2,} & {\text { if } x \geq 2}\end{array}\right.\right. \nonumber \]

Our number line and piecewise definition agree: $|x-2|=-(x-2)$ to the left of 2 and $|x-2|=x-2$ to the right of 2. Further, note how we’ve included the critical value of 2 “on the right” in our piecewise definition.

Let’s summarize the method we followed to construct the piecewise function above.

Constructing a Piecewise Definition for Absolute Value

When presented with the absolute value of an algebraic expression, perform the following steps to remove the absolute value bars and construct an equivalent piecewise definition.

Take the expression that is inside the absolute value bars, and set that expression equal to zero. Then solve for x. This value of $x$ is called a “critical value.” (Note: The expression inside the absolute value bars could have more than one critical value. We will not encounter such problems in this text.)
Place your critical value on a number line.
Place the expression inside the absolute value bars below the number line at the left end.
Test the sign of the expression inside the absolute value bars by inserting a value of $x$ from each side of the critical value and marking the result with a plus (+) or minus (-) sign below the number line.
Place the original expression, the one including the absolute value bars, above the number line at the left end.
Use the sign of the expression inside the absolute value bars (indicated by the plus and minus signs below the number line) to remove the absolute value bars, placing the results above the number line on each side of the critical value.
Construct a piecewise definition that organizes the results on the number line.

Try It 1

Determine a piecewise definition for $y=|x+1|$

Answer

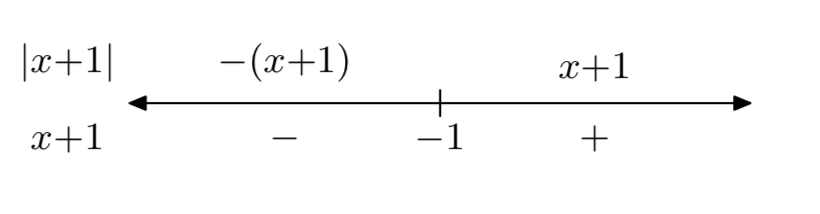
$Screen Shot 2019-09-09 at 3.12.13 PM.png$

\[f(x)=\left\{\begin{array}{ll}{-x-1,} & {\text { if } x<-1} \\ {x+1,} & {\text { if } x \ge -1} \nonumber \end{array}\right. \nonumber \]

Let’s apply this technique to another example.

Example 2

Determine a piecewise definition for $|3-2x|$.

Solution

Step 1: First set the expression inside the absolute value bars equal to zero and solve for $x$.

\[\begin{aligned} 3-2x &=0 \\ x &=3 / 2 \end{aligned} \nonumber \]

Note that $3-2x=0$ at $x=\frac{3}{2}$. This is the “critical value” for this expression.

Steps 2 and 3: Draw a number line and mark this critical value on the line. The next step requires that we place the expression inside the absolute value bars, namely $3 - 2x$, underneath the line at its left end.

$WeChatf8b53e9cd145037bb92c2487876b4dcc.png$

Step 4: Next, determine the sign of $3 - 2x$ for values of $x$ on each side of $\frac{3}{2}$. This is easily done by “testing” a point on each side of $\frac{3}{2}$ in the expression $3 - 2x$.

Take $x = 1$, which lies to the left of $\frac{3}{2}$. Substitute this value of $x$ into the expression $3 - 2x$, obtaining \[3-2 x=3-2(1)=1 \nonumber \] which is positive. Indicate this result by placing a plus sign (+) below the number line to the left of $\frac{3}{2}$.
Next, pick $x = 2$, which lies to the right of $\frac{3}{2}$. Substitute this value of $x$ into the expression $3 - 2x$, obtaining \[3-2 x=3-2(2)=-1 \nonumber \] which is negative. Indicate this result by placing a negative sign (-) below the line to the right of $\frac{3}{2}$ (see the number line above).

$WeChat8da60f46fba3967ac0b8402201967d12.png$

Steps 5 and 6: Place the original expression, namely $|3-2x|$, above the number line at the left end. The next step is to remove the absolute value bars from the expression $|3-2x|$.

To the left of $\frac{3}{2}$, the expression $3 - 2x$ is positive (note the plus sign (+) below the number line), so $|3-2x| = 3-2x$. Indicate this result by placing the expression $3 - 2x$ above the number line to the left of $\frac{3}{2}$.
To the right of $\frac{3}{2}$, the expression $3-2x$ is negative (note the minus sign (-) below the numberline), so $|3-2x| = -(3-2x)$. That is, we have to negate $3-2x$ to make it positive. This is indicated by placing the expression $-(3 - 2x)$ above the line to the right of $\frac{3}{2}$.

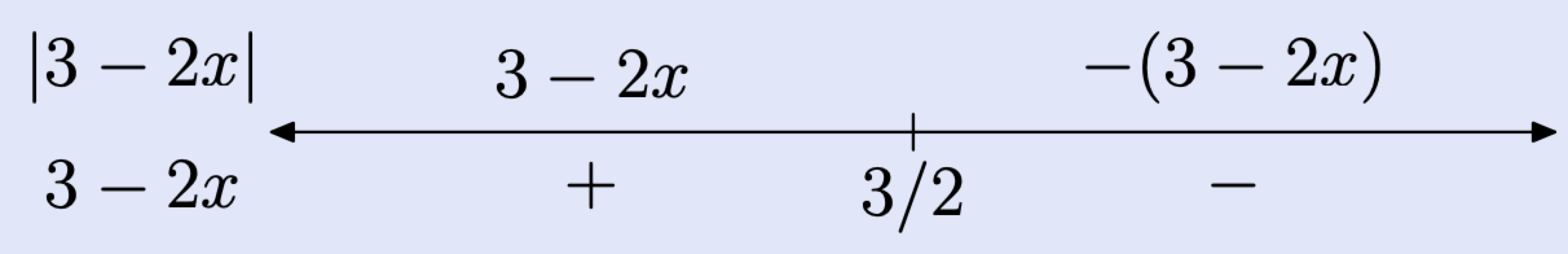
$WeChate88fa939bcad9116505b9db0e36610c4.png$

Step 7: We can use this last number line summary to write a piecewise definition for the expression $|3 - 2x|$.

\[|3-2 x|=\left\{\begin{array}{ll}{3-2 x,} & {\text { if } x<3 / 2 .} \\ {-(3-2 x),} & {\text { if } x \geq 3 / 2}\end{array}=\left\{\begin{array}{ll}{3-2 x,} & {\text { if } x<3 / 2} \\ {-3+2 x,} & {\text { if } x \geq 3 / 2}\end{array}\right.\right. \nonumber \]

Again, note how we’ve included the critical value of $\frac{3}{2}$ “on the right.”

Try It 2

Determine the piecewise definition for $y=|4-5x|$.

Answer

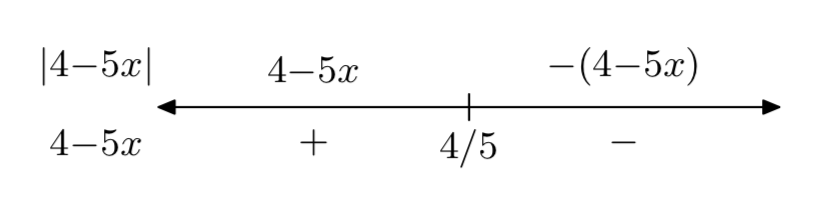
$Screen Shot 2019-09-09 at 3.14.38 PM.png$

\[g(x)=\left\{\begin{array}{ll}{4-5x,} & {\text { if } x<\frac{4}{5}} \\ {-4+5x,} & {\text { if } x \ge \frac{4}{5}} \nonumber \end{array}\right. \nonumber \]

Drawing the Graph of an Absolute Value Equation

Now that we know how to construct a piecewise definition for an expression containing absolute value bars, we can use what we know about graphing lines.

Consider again the basic definition of the absolute value of $x$.

\[y=|x|=\left\{\begin{array}{ll}{-x,} & {\text { if } x<0} \\ {x,} & {\text { if } x \geq 0}\end{array}\right. \nonumber \]

Some basic observations are:

If $x<0$, then $y=-x$. This ray starts at the origin and extends to the left with slope -1. Its graph is pictured on the left in the figure below.
If $x \geq 0$, then $y=x$. This ray starts at the origin and extends to the right with slope 1. Its graph is pictured in the center of the figure below.
We combine these graphs to produce the graph of $y=|x|$, pictured on the right in the figure below.

$clipboard_ea03dbafa2c23e2fdab56806bd0655705.png$

You should commit the graph of $y=|x|$ to memory. Things to note:

The graph of $y=|x|$ is “V-shaped.”
The vertex of the graph is at the point $(0,0)$.
The left-hand branch has the equation $y=-x$ and a slope of -1.
The right-hand branch has the equation $y=x$ and a slope of 1.

Now that we know how to draw the graph of $y=|x|$, we can sketch a number of simple graphs involving absolute value.

Example 3

Sketch a graph of $y=|x+1|$

Solution

We constructed the following piecewise definition of $ y = |x + 1| $:

\[
y = |x + 1| =
\begin{cases}
-(x + 1), & \text{if } x < -1 \\
x + 1, & \text{if } x \geq -1
\end{cases}
\nonumber \]

We now sketch each piece of this equation based on its definition.

If $ x < -1 $, then $ y = -(x + 1) $. This defines a ray starting at $ x = -1 $ and extending to the left. To find the endpoint of the ray, evaluate $ y = -(x + 1) $ at $ x = -1 $:

\[
y = -(-1 + 1) = -0 = 0
\nonumber\]

Thus, the endpoint of the ray is located at $ (-1, 0) $. Since $ x $ must be strictly less than $-1$, this endpoint is shown as an open circle on the graph.

Next, choose a value of $ x $ to the left of $-1$, such as $ x = -2 $, to find another point:

\[
y = -(-2 + 1) = -(-1) = 1
\nonumber\]

Thus, a second point on the ray is $ (-2, 1) $. Using these points, we construct a graph containing the two evaluated points and a ray connecting them.

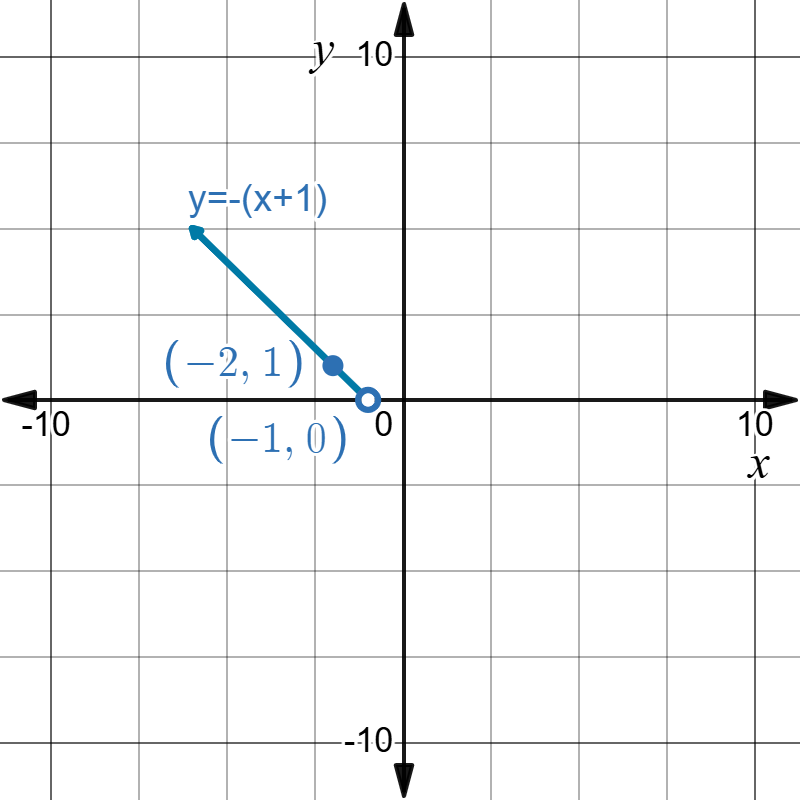$desmos-graph (1).png$

If $ x \geq -1 $, then $ y = x + 1 $. This defines a ray starting at $ x = -1 $ and extending to the right. Evaluate $ y = x + 1 $ at $ x = -1 $:

\[
y = -1 + 1 = 0
\nonumber\]

So the endpoint of the ray is at $ (-1, 0) $. Since $ x $ may equal $-1$ in this case, the endpoint is shown as a closed circle on the graph.

Now pick a value of $ x $ to the right of $-1$, such as $ x = 1 $:

\[
y = 1 + 1 = 2
\nonumber\]

Thus, another point on the ray is $ (1, 2) $. Using these points, we construct a graph containing the two evaluated points and a ray connecting them.

$desmos-graph (2).png$

To sketch the graph of $ y = |x + 1| $, we combine the two rays we just graphed.

$desmos-graph (5).png$

Note the “V-shape” of the graph. We will refer to the point at the tip of the “V” as the vertex of the absolute value function.

Try It 3

Sketch the graph of $y=|x-3|$.

Answer: $clipboard_e80a836e7afbe1e2036e2bcbc94961f6c.png$

Example 4

Sketch the graph of $y=|3-2x|$.

Solution

We constructed the following piecewise definition of $y=|3-2x|$ in an earlier example.

\[y=|3-2 x|=\left\{\begin{array}{ll}{3-2 x,} & {\text { if } x<3 / 2} \\ {-3+2 x,} & {\text { if } x \geq 3 / 2}\end{array}\right. \nonumber \]

We now sketch each piece of this equation based on its definition.

If $x<\frac{3}{2}$, then $y=3-2x$. This defines a ray, starting at $x=\frac{3}{2}$ and extending to the left. We first find the endpoints of the ray by evaluating $y=3-2x$ at $x=\frac{3}{2}$

\[y=3-2(3 / 2)=3-3=0 \nonumber \]

Thus, the endpoint of the ray is located at $(\frac{3}{2},0)$. Since $x$ must be strictly less than $\frac{3}{2}$, this endpoint is shown as an open circle on the graph.

Next, pick a value of $x$ that lies to the left of $\frac{3}{2}$, such as $x=0$, to find another point on the ray.

\[y=3-2(0)=3-0=3 \nonumber \]

Thus, a second point on the ray is $(0,3)$. Using these points, we construct a graph containing the two evaluated points and a ray connecting them.

$clipboard_e58038edabe3deb8da1b675e60302c907.png$

If $x≥\frac{3}{2}$, then $y=-3+2x$. This is a ray, starting at $x=\frac{3}{2}$ and extending to the right. We find the endpoint of the ray by evaluating $y=-3+2x$ at $x=\frac{3}{2}$, \[y=-3+2(3 / 2)=-3+3=0 \nonumber \]

Thus, the endpoint of the ray is located at $(\frac{3}{2},0)$. Since $x$ may equal $\frac{3}{2}$ in this case, the endpoint is shown as a closed circle on the graph.

Next, to find another point on the ray, pick a value of $x$ that lies to the right of $\frac{3}{2}$ such as $x=3$, \[y=-3+2(3)=-3+6=3 \nonumber \]

Thus, a second point on the ray is $(3,3)$. Using these points, we construct a graph containing the two evaluated points and a ray connecting them.

$clipboard_ee4e8a483fba9db3c59c6ad32724573f5.png$

To sketch the graph of $y=|3-2x|$, we need only combine the two pieces from the two rays we previously graphed.

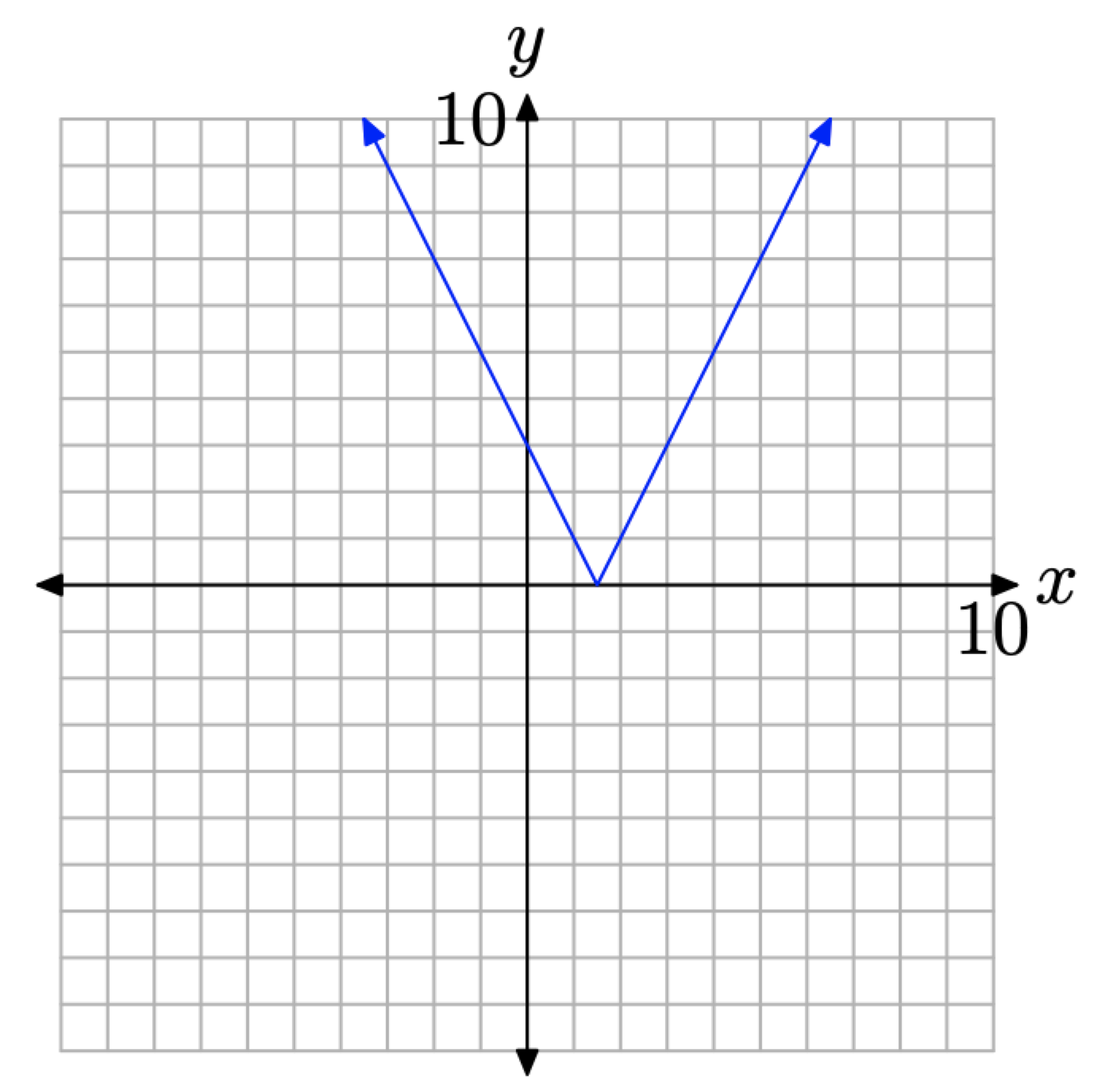
$WeChatb2a984d19c2b20f7acf88440c04a68d2.png$

In this graph, the equation of the left-hand branch of the “V” is $y=3-2x$. An alternative approach to drawing this branch is to note that its graph is contained within the graph of the whole line $y=3-2x$, which has a slope of -2 and a $y$-intercept at $(0,3)$. Thus, one could draw the entire line using the slope and $y$-intercept, then erase the part of the line that lies to the right of $x=\frac{3}{2}$. A similar strategy would work for the right-hand branch of $y=|3-2x|$.

Try It 4

Sketch a graph for $y=|1-3x|$.

Answer

\[y=\left\{\begin{array}{ll}{1-3x,} & {\text { if } x<\frac{1}{3}} \\ {-1+3x,} & {\text { if } x \ge \frac{1}{3}} \nonumber \end{array}\right. \nonumber \]

$Screen Shot 2019-09-09 at 3.25.35 PM.png$

Search

Text Color

Text Size

Margin Size

Font Type

Motivating Problem

Fun Fact

The Goal

Definition: Absolute Value

Summarizing the Definition on a Number Line

Definition

Example 1

Solution

Constructing a Piecewise Definition for Absolute Value

Try It 1

Example 2

Solution

Try It 2

Example 3

Solution

Try It 3

Example 4

Solution

Try It 4