Section 3.3: Absolute Value Inequalities
- Page ID
- 192824
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We will rely heavily on these skills throughout this section.
- Solve \(-x+4<7\) for \(x\)
- Graph the inequality \(y<x-5\)
- Determine if \(x=\frac{3}{2}\) makes \(|x-2|<2\) true.
Motivating Problem
You’re baking cookies that need to be in the oven at exactly 350°F. The oven manual says it fluctuates by up to 15°F during baking. What temperature range should you expect, and how can you express that as a mathematical sentence?
Fun Fact
Astronomers use absolute value inequalities to describe how far off a measurement can be when locating distant stars or planets. Even tiny errors—like being off by 0.001 light-years—can lead to big navigational mistakes!
The Goal
In this section, we’ll learn to solve absolute value inequalities by translating them into statements about distance. We'll explore symbolic strategies and use Desmos to graph and visually analyze solution sets.
Solve Absolute Value Inequalities with “Less Than”
Let’s look now at what happens when we have an absolute value inequality. Everything we’ve learned about solving inequalities still holds, but we must consider how the absolute value impacts our work. Again, we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line. For the equation \(|x|=5\), we saw that both 5 and \(-5\) are five units from zero on the number line. They are the solutions to the equation.
\[\begin{array} {lll} {} &{|x|=5} &{} \\ {x=-5} &{\text{or}} &{x=5} \\ \nonumber \end{array}\]
What about the inequality \(|x|\leq 5\)? Where are the numbers whose distance is less than or equal to 5? We know \(-5\) and 5 are both five units from zero. All the numbers between \(-5\) and 5 are less than five units from zero.
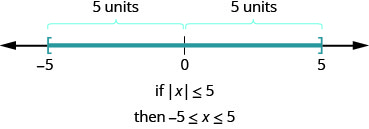
Let's visualize this graphically. Consider the graphs of \(y=|x|\) and \(y=5\). The solutions consist of all \(x\)-values where the graph of \(y=|x|\) is less than, or equal to, the graph of \(y=5\). Because we are comparing \(y\) values, "less than" is below vertically.
.png?revision=1&size=bestfit&width=447&height=298)
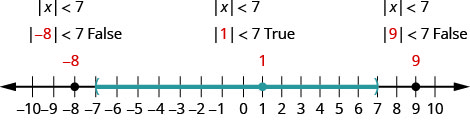
In this case, we see that the red portion of \(|x|\) satisfies the inequality \(|x|\leq5\). Therefore, the solution is \(x\) in \([-5,5]\).
In a more general way, we can see that if \(|u|\leq a\), then \(-a\leq u\leq a\).
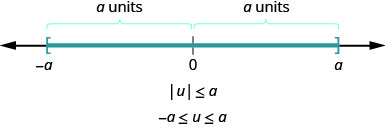
This result is summarized here.
For any algebraic expression, u, and any positive real number, a,
\[ \text{if} \quad |u|<a, \quad \text{then} \space -a<u<a \\ \text{if} \quad |u|\leq a, \quad \text{then} \space-a\leq u\leq a \nonumber\]
After solving an inequality, it is often helpful to check some points to see if the solution makes sense. The graph of the solution divides the number line into three sections. Choose a value in each section and substitute it in the original inequality to see if it makes the inequality true or not. While this is not a complete check, it often helps verify the solution.
Solve \(|x|<7\). Graph the solution on a number line and write the solution in interval notation.
Solution
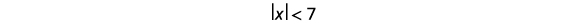 |
|
| Write the equivalent inequality. | 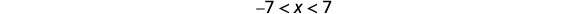 |
| Graph the solution. | 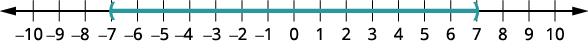 |
| Write the solution using interval notation. | 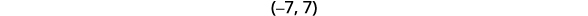 |
Check:
To verify, check a value in each section of the number line showing the solution. Choose numbers such as -8, 1, and 9.
Graph the solution on a number line and write the solution in interval notation: \(|x|<9\).
- Answer
-
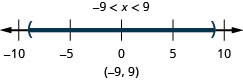
In this section, we will solve absolute value inequalities in two ways: with algebra and with graphs.
In the algebra method, we remove the absolute value bars by using the definition of absolute value. This often gives us two separate inequalities to solve. We then solve them using the same steps we use for regular linear inequalities.
In the graph method, we draw both sides of the inequality on the same coordinate plane. Then we look for the parts of the \(x\)-axis where the absolute value graph satisfies the inequality.
Using both methods helps us check our answers and understand how absolute value inequalities work.
Solve using algebraic and graphical methods: \(|x+2|<3\).
Solution
To solve algebraically, we bound the argument \(x+2\) by \(−3\) and \(3\) and solve.
\[\begin{array} { c } { | x + 2 | < 3 } \\ { - 3 < x + 2 < 3 } \\ { - 3 \color{Cerulean}{- 2}\color{Black}{ <} x + 2 \color{Cerulean}{- 2}\color{Black}{ <} 3 \color{Cerulean}{- 2} } \\ { - 5 < x < 1 } \end{array}\nonumber\]
To solve the system graphically, we graph both \(y=|x+2|\) and \(y=3\) to determine on what interval the absolute value graph is less than (or below) the linear graph.
.png?revision=1&size=bestfit&width=430&height=286)
Using both approaches, we determine the solution to be all \(x\) in the interval \((-5,1)\).
Solve using algebraic and graphical methods: \(|x-3|<5\)
- Answer
-
All \(x\) in the interval \((-2,8)\).
Solve using algebraic and graphical methods: \(|5x-6|\leq 4\).
Solution
To solve algebraically, we bound the argument \(5x - 6\) by \(-4\) and \(4\) and solve.
\[
\begin{array}{c}
|5x - 6| \leq 4 \\
-4 \leq 5x - 6 \leq 4 \\
-4 \color{Cerulean}{+ 6} \color{Black}{\leq} 5x - 6 \color{Cerulean}{+ 6} \color{Black}{\leq} 4 \color{Cerulean}{+ 6} \\
2 \leq 5x \leq 10 \\
\dfrac{2}{5} \leq x \leq 2
\end{array}
\nonumber\]
To solve the system graphically, we graph both \(y = |5x - 6|\) and \(y = 4\) to determine on what interval the absolute value graph is less than or equal to the linear graph.
.png?revision=1&size=bestfit&width=429&height=286)
Using both approaches, we determine the solution to be all \(x\) in the interval \(\left[\dfrac{2}{5},2\right]\).
Solve using algebraic and graphical methods: \(|2x-1|\leq 5\)
- Answer
-
All \(x\) in the interval \([-2,3]\).
- Isolate the absolute value expression.
- Write the equivalent compound inequality.
\[\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{-a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{-a\leq u\leq a} \\ \nonumber \end{array}\]
- Solve the compound inequality.
- Graph the solution
- Write the solution using interval notation.
Solve Absolute Value Inequalities with “Greater Than”
What happens for absolute value inequalities that have “greater than”? Again, we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line.
Now we want to look at the inequality \(|x|\geq 5\). Where are the numbers whose distance from zero is greater than or equal to five?
Again, both \(-5 \) and 5 are five units from zero and so are included in the solution. Numbers whose distance from zero is greater than five units would be less than \(-5\) or greater than 5 on the number line.
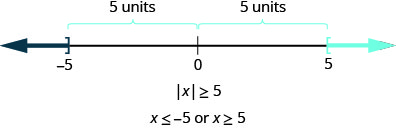
Let's visualize this graphically. Consider the graphs of \(y=|x|\) and \(y=5\). The solutions consist of all \(x\)-values where the graph of \(y=|x|\) is greater than, or equal to, the graph of \(y=5\). Because we are comparing \(y\) values, "greater than" is above vertically.
.png?revision=1&size=bestfit&width=452&height=301)
In this case, we see that the red portions of \(|x|\) satisfy the inequality \(|x|\geq5\), so the solution has two parts. The left portion corresponds to \(x\) less than or equal to -5: \((-\infty,-5]\). The right portion corresponds to \(x\) greater than or equal to 5: \([5,\infty)\). We can use the union symbol, \(\cup\), to represent "or" and the solution becomes \((-\infty,-5]\cup[5,\infty)\).
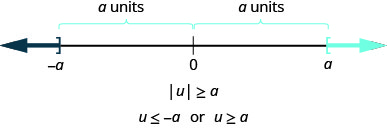
In a more general way, we can see that if \(|u|\geq a\), then \(u\leq -a\) or \(u\geq a\).
This result is summarized here.
For any algebraic expression, u, and any positive real number, a,
\[\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\quad \text{then } u<-a \text{ or } u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\quad \text{then } u\leq -a \text{ or } u\geq a} \\ \nonumber \end{array}\]
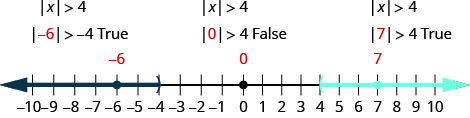
Solve \(|x|>4\). Graph the solution on a number line and write the solution in interval notation.
Solution
| \(|x|>4\) | |
| Write the equivalent inequality. | \(x<−4\) or \(x>4\) |
| Graph the solution. |  |
| Write the solution using interval notation. | \((−\infty ,−4)\cup (4,\infty )\) |
| Check: |
To verify, check a value in each section of the number line showing the solution. Choose numbers such as −6, 0, and 7.
Solve \(|x|>2\). Graph the solution and write the solution in interval notation.
- Answer
-
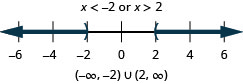
Solve using algebraic and graphical methods: \(|x+2|>3\).
Solution
To solve algebraically, we consider the two cases where \(x + 2\) is greater than \(3\) or less than \(-3\).
\[
\begin{array}{c}
|x + 2| > 3 \\
x + 2 < -3 \quad\text{or}\quad x + 2 > 3 \\
x < -5 \quad\quad\quad\quad\quad\quad\quad\quad x > 1
\end{array}
\nonumber\]
To solve the system graphically, we graph both \(y = |x + 2|\) and \(y = 3\) to determine for which values of \(x\) the absolute value graph is greater than the constant graph.
.png?revision=1&size=bestfit&width=477&height=318)
Using both approaches, we determine the solution to be all \(x\) in the interval \((-\infty,-5)\cup(1,\infty)\).
Solve using algebraic and graphical methods: \(|4x-3|\geq 5\).
- Answer
-
All \(x\) in the interval \(\left(-\infty,-\dfrac{1}{2}\right]\cup[2,\infty)\).
- Isolate the absolute value expression.
- Write the equivalent compound inequality.
\[\begin{array} {lll}
{ |u| >a } &{\quad \text{is equivalent to}} &{ u<-a \quad \text{ or } \quad u>a}
\\ { |u| \geq a } &{\quad \text{is equivalent to}} &{ u\leq -a \quad \text{ or } \quad u\geq a}
\\ \nonumber \end{array}\] - Solve the compound inequality.
- Graph the solution
- Write the solution using interval notation.
Solve Applications with Absolute Value
Absolute value inequalities are often used in the manufacturing process. An item must be made with near-perfect specifications. Usually, there is a certain tolerance for the difference from the specifications that is allowed. If the difference from the specifications exceeds the tolerance, the item is rejected.
\[|\text{actual-ideal}|\leq \text{tolerance} \nonumber\]
The ideal diameter of a rod needed for a machine is 60 mm. The actual diameter can vary from the ideal diameter by \(0.075\) mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?
Solution
\(\begin{array} {ll} {} &{\text{Let }x=\text{ the actual measurement}} \\ {\text{Use an absolute value inequality to express this situation.}} &{|\text{actual-ideal}|\leq \text{tolerance}} \\ {} &{|x-60|\leq 0.075} \\ {\text{Rewrite as a compound inequality.}} &{-0.075\leq x-60\leq 0.075} \\ {\text{Solve the inequality.}} &{59.925\leq x\leq 60.075} \\ {\text{Answer the question.}} &{\text{The diameter of the rod can be between}} \\ {} &{59.925 \text{ and } 60.075 \text{ mm.}} \\ \end{array}\)
The ideal diameter of a rod needed for a machine is 75 mm. The actual diameter can vary from the ideal diameter by 0.05 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?
- Answer
-
The diameter of the rod can be between 74.95 and 75.05 mm.


