Section 3.6: Line Equations

Last updated
Save as PDF

Page ID: 188509

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Be Prepared

We will rely heavily on these skills throughout this section.

Determine the slope of the line $ y = \frac{1}{2}x - 1 $
Determine whether the point $ (4, 1) $ lies on the line $ y = -x + 5 $
Find the y-intercept of the equation $ 4x - 2y = 10 $

Learning Objectives

Motivating Problem

You’re designing a wheelchair ramp that must rise 2 feet for every 12 feet of horizontal run. The ramp starts at ground level in front of the entrance. If someone asks you to describe the slope of the ramp and write an equation to model its incline, what form should you use—and how do you decide?

Fun Fact

The idea of using different forms to represent lines dates back to early analytic geometry. French mathematician François Viète laid the groundwork in the 1500s, and later, Descartes formalized it—giving us the flexible language of line equations we still use today.

The Goal

In this section, we won’t just plug into formulas—we’ll learn how to build equations of lines based on the information we have. Whether we’re given a slope and a point, two points, or a relationship like “parallel to” or “perpendicular to,” we’ll decide which method fits the situation and write the equation that models it.

To create a mathematical model of a linear relation between two variables, we must be able to find the equation of the line. In this section, we will look at several ways to write the equation of a line. The specific method we use will be determined by what information we are given.

Find an Equation of the Line Given the Slope and $y$-Intercept

If the equation is written in slope-intercept form, $y=mx+b$, we can easily determine the slope and $y$-intercept of a line. Now, we will do the reverse—we will start with the slope and $y$-intercept and use them to find the equation of the line.

Example 1

Find an equation of a line with slope -7 and $y$-intercept $(0,-1)$.

Solution

Since we are given the slope and $y$-intercept of the line, we can substitute the necessary values into the slope–intercept form, $y=mx+b$.

Name the slope.	$.$
Name the $y$-intercept.	$.$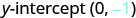
Substitute the values into y=mx+b.	$.$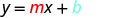
	$.$
	$.$

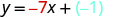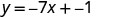Try It 1

a. Find an equation of a line with slope $\frac{2}{5}$ and $y$-intercept $(0,4)$.

b. Find an equation of a line with slope -1 and $y$-intercept $(0,-3)$.

Answer

a. $y = \frac{2}{5}x + 4$

b. $y=-x-3$

Sometimes, the slope and intercept need to be determined from the graph.

Example 2

Find the equation of the line shown.

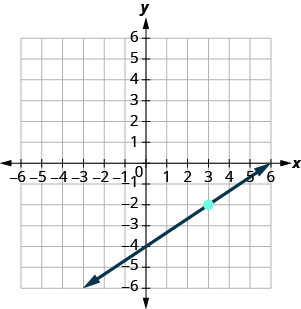
$The graph shows the x y-coordinate plane. The x and y-axes each run from negative 7 to 7. A line intercepts the y-axis at (0, negative 4), passes through the plotted point (3, negative 2), and intercepts the x-axis at (4, 0).$

Solution

We need to find the slope and $y$-intercept of the line from the graph so that we can substitute the necessary values into the slope–intercept form, $y=mx+b$.

To find the slope, we choose two points on the graph.

The $y$-intercept is $(0,-4)$ and the graph passes through $(3,-2)$.

Find the slope by counting the rise and run.	$.$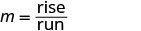
	$.$
Find the $y$-intercept.	$.$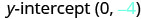
Substitute the values into $y=mx+b$.	$.$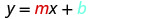
	$.$

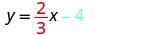Try It 2

Find the equation of the line shown in the graph.

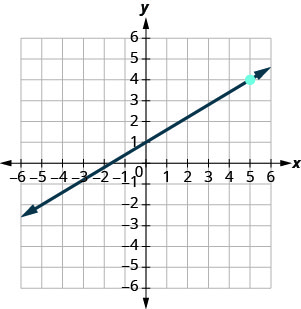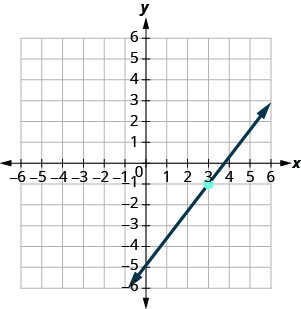
a. $The graph shows the x y-coordinate plane. The x and y-axes each run from negative 7 to 7. A line intercepts the x-axis at (negative 2, 0), intercepts the y-axis at (0, 1) and passes through the plotted point (5, 4).$ b. $The graph shows the x y-coordinate plane. The x and y-axes each run from negative 7 to 7. A line intercepts the y-axis at (0, negative 5), passes through the plotted point (3, negative 1), and intercepts the x-axis at (15 fourths, 0).$

Answer

a. $y=\frac{3}{5}x+1$

b. $y=\frac{4}{3}x-5$

Find an Equation of the Line Given the Slope and a Point

Finding an equation of a line using the slope–intercept form of the equation works well when you are given the slope and $y$-intercept or when you read them off a graph. But what happens when you have another point instead of the $y$-intercept?

We will use the slope formula to derive another form of the line's equation. Suppose we have a line that has slope $m$ and that contains some specific point $(x_{1}, y_{1})$ and some other point, which we will just call $(x,y)$. We can write the slope of this line and then change it to a different form.

$\begin{array} {lrll}&m &=\frac{y-y_{1}}{x-x_{1}} \\ \text{Multiply both sides of the equation by }x-x_{1}.&m\left(x-x_{1}\right) &=\left(\frac{y-y_{1}}{x-x_{1}}\right)\left(x-x_{1}\right) \\ \text{Simplify.}&m\left(x-x_{1}\right) &=y-y_{1} \\ \text{Rewrite the equation with the \(y$ terms on the left.} &y-y_{1} &=m\left(x-x_{1}\right) \end{array}\)

This format is known as the point–slope form of a line's equation.

POINT–SLOPE FORM OF AN EQUATION OF A LINE

The point–slope form of an equation of a line with slope $m$ and containing the point $(x_{1}, y_{1})$ is

\[y-y_{1}=m(x-x_{1})\nonumber\]

We can use the point–slope form of an equation to find the equation of a line when given the slope and one point. We will then rewrite the equation in slope–intercept form. Most applications of linear equations use the slope–intercept form.

FIND AN EQUATION OF A LINE GIVEN THE SLOPE AND A POINT.

Identify the slope.
Identify the point.
Substitute the values into the point-slope form, $y-y_{1}=m(x-x_{1})$.
Write the equation in slope–intercept form.

Example 3

Find an equation of a line with slope $m=-\frac{1}{3}$ that contains the point $(6,-4)$. Write the equation in slope–intercept form.

Solution

Since we are given a point and the slope of the line, we can substitute the needed values into the point–slope form, $y-y_{1}=m(x-x_{1})$.

Identify the slope.	$.$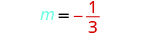
Identify the point.	$.$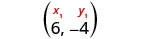
Substitute the values into $y-y_{1}=m(x-x_{1})$.	$.$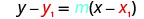
	$.$
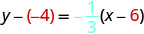Simplify.	$.$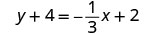
Write in slope–intercept form.	$.$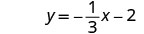

Try It 3

Find an equation of a line with slope $m=-\frac{2}{5}$ and containing the point $(10,-5)$.

Answer: $y=-\frac{2}{5}x-1$

Example 4

Find an equation of a horizontal line that contains the point $(-1,2)$. Write the equation in slope–intercept form.

Solution

Every horizontal line has slope 0. We can substitute the slope and points into the point–slope form, $y-y_{1}=m(x-x_{1})$.

Identify the slope.	$.$
Identify the point.	$.$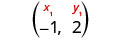
Substitute the values into $y-y_{1}=m(x-x_{1})$.	$.$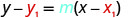
	$.$
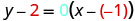Simplify.	$.$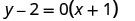
	$.$
	$.$
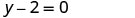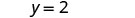Write in slope–intercept form.	It is in $y$-form, but could be written as $y=0x+2$.

Try It 4

a. Find an equation of a vertical line containing the point $(-3,8)$.

b. Find an equation of a horizontal line containing the point $(-1,4)$.

Answer

a. $x=-3$

b. $y = 4$

Find an Equation of the Line Given Two Points

When real-world data is collected, a linear model can be created from two data points. In the next example, we’ll see how to find the equation of a line when just two points are given.

We have two options so far for finding the equation of a line: the slope–intercept form or the point–slope form. Since we will know two points, we will use the point–slope form.

FIND AN EQUATION OF A LINE GIVEN TWO POINTS.

Find the slope using the given points.
Choose one point.
Substitute the values into the point-slope form, $y-y_{1}=m(x-x_{1})$.
Write the equation in slope–intercept form.

Example 5

Find an equation of a line that contains the points $(-3,-1)$ and $(2,-2)$. Write the equation in slope–intercept form.

Solution

Since we have two points, we will find an equation of the line using the point–slope form. The first step will be to find the slope.

Find the slope of the line through $(-3,-1)$ and $(2,-2)$.	$.$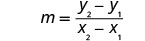
	$.$
	$.$
	$.$
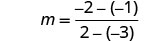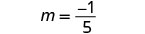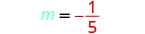Choose either point.	$.$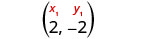
Substitute the values into $y-y_{1}=m(x-x_{1})$.	$.$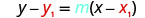
	$.$
	$.$
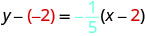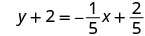Write in slope–intercept form.	$.$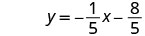

Try It 5

Find an equation of a line containing the points $(-2,-4)$ and $(1,-3)$.

Answer: $y=\frac{1}{3}x-\frac{10}{3}$

Example 6

Find an equation of a line that contains the points $(-2,4)$ and $(-2,-3)$. Write the equation in slope–intercept form.

Solution

Again, the first step will be to find the slope.

$\begin{array}{lrl} \text { Find the slope of the line through }(-2,4) \text { and }(-2,-3) & & &\\ &m &=&\frac{y_{2}-x_{1}}{x_{2}-x_{1}} \\ &m &=&\frac{-3-4}{-2-(-2)} \\ &m &= &\frac{-7}{0} \\ \\ \text { The slope is undefined. } & & &\end{array}$

This tells us it is a vertical line. Both of our points have an $x$-coordinate of -2. So our equation of the line is $x=-2$. Since there is no $y$, we cannot write it in slope–intercept form.

You may want to sketch a graph using the two given points. Does the graph agree with our conclusion that this is a vertical line?

Try It 6

Find an equation of a line containing the points $(5,1)$ and $(5,-4)$.

Answer: $x=5$

We have seen that we can use either the slope–intercept form or the point–slope form to find the equation of a line. Which form we use will depend on the information we are given. This is summarized below.


To Write an Equation of a Line
If given:	Use:	Form:
Slope and $y$-intercept	slope–intercept	$y=mx+b$
Slope and a point	point–slope	$y-y_{1}=m(x-x_{1})$
Two points	point–slope	$y-y_{1}=m(x-x_{1})$

Find an Equation of a Line Parallel to a Given Line

Suppose we need to find an equation of a line that passes through a specific point and is parallel to a given line. We can use the fact that parallel lines have the same slope. So we will have a point and the slope, just what we need to use the point–slope equation.

First, let’s look at this graphically.

The graph shows the graph of $y=2x-3$. We want to graph a line parallel to this line and passing through the point $(-2,1)$.

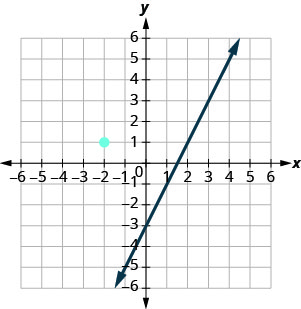
The graph shows the x y-coordinate plane. The x and y-axes each run from negative 7 to 7. The line whose equation is y equals 2x minus 3 intercepts the y-axis at (0, negative 3) and intercepts the x-axis at (3 halves, 0). Elsewhere on the graph, the point (negative 2, 1) is plotted.

We know that parallel lines have the same slope. So, the second line will have the same slope as $y=2x-3$. That slope is $m_{\|} = 2$. We’ll use the notation $m_{\|}$ to represent the slope of a line parallel to a line with slope m. (Notice that the subscript ∥ looks like two parallel lines.)

The second line will pass through $(-2,1)$ and have $m=2$. To graph the line, we start at $(-2,1)$ and count out the rise and run. With $m=2$ (or $m=\frac{2}{1}$), we count out the rise 2 and the run 1. We draw the line.

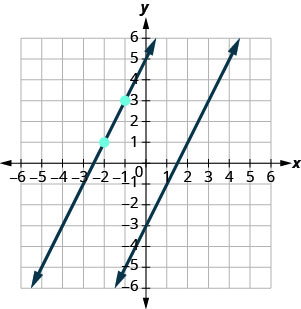
Do the lines appear parallel? Does the second line pass through $(-2,1)$?

Now, let’s see how to do this algebraically.

We can use either the slope–intercept form or the point–slope form to find the equation of a line. Here we know one point and can find the slope. So we will use the point–slope form.

Example 7

Find an equation of a line parallel to $y=2x-3$ that contains the point $(-2,1)$. Write the equation in slope–intercept form.

Solution

$This figure is a table that has three columns and four rows. The first column is a header column, and it contains the names and numbers of each step. The second column contains further written instructions. The third column contains math. In the first row of the table, the first cell on the left reads: “Step 1. Find the slope of the given line.” The second cell reads: “The line is in slope-intercept form. y equals 2x minus 3.” The third cell contains the slope of a line, defined as m equals 2.$ $In the second row, the first cell reads: “Step 2. Find the slope of the parallel line.” The second cell reads “Parallel lines have the same slope.” The third cell contains the slope of the parallel line, defined as m parallel equals 2.$ $In the third row, the first cell reads “Step 3. Identify the point.” The second cell reads “The given point is (negative 2, 1).” The third cell contains the ordered pair (negative 2, 1) with a superscript x subscript 1 above negative 2 and a superscript y subscript 1 above 1.$ $In the fourth row, the first cell reads “Step 4. Substitute the values into the point-slope form, y minus y subscript 1 equals m times x minus x subscript 1 in parentheses.” The top of the second cell is blank. The third cell contains the point-slope form, y minus y subscript 1 equals m times x minus x subscript 1 in parentheses. Below this is the form with negative 2 substituted for x subscript 1, 1 substituted for y subscript 1, and 2 substituted for m: y minus 1 equals 2 times x minus negative 2 in parentheses. One line down, the text in the second cell says “Simplify.” The right column contains y minus 1 equals 2 times x plus 2. Below this is y minus 1 equals 2x plus 4.$ $In the fifth row, the first cell says “Step 5. Write the equation in slope-intercept form.” The second cell is blank. The third cell contains y equals 2x plus 5.$

Does this equation make sense? What is the $y$-intercept of the line? What is the slope?

Try It 7

Find an equation of a line parallel to the line $y=\frac{1}{2}x-3$ that contains the point $(6,4)$.

Answer: $y=\frac{1}{2}x+1$

FIND AN EQUATION OF A LINE PARALLEL TO A GIVEN LINE.

Find the slope of the given line.
Find the slope of the parallel line.
Identify the point.
Substitute the values into the point–slope form, $y-y_{1}=m(x-x_{1})$.
Write the equation in slope–intercept form.

Find an Equation of a Line Perpendicular to a Given Line

Now, let’s consider perpendicular lines. Suppose we need to find a line that passes through a specific point and is perpendicular to a given line. We can use the fact that perpendicular lines have slopes that are negative reciprocals of each other. We will again use the point–slope equation, like we did with parallel lines.

The graph shows the graph of $y=2x-3$. Now, we want to graph a line perpendicular to this line and passing through $(-2,1)$.

We know that perpendicular lines have slopes that are negative reciprocals. We’ll use the notation $m_{\perp}$ to represent the slope of a line perpendicular to a line with slope m. (Notice that the subscript $_{\perp}$ looks like the right angles made by two perpendicular lines.)

\[\begin{array}{cl}{y=2 x-3} & {\text { perpendicular line }} \\ {m=2} & {m_{\perp}=-\frac{1}{2}}\end{array}\nonumber\]

We now know the perpendicular line will pass through $(-2,1)$ with $m_{\perp}=-\frac{1}{2}$.

To graph the line, we will start at $(-2,1)$ and count out the rise -1 and the run 2. Then we draw the line.

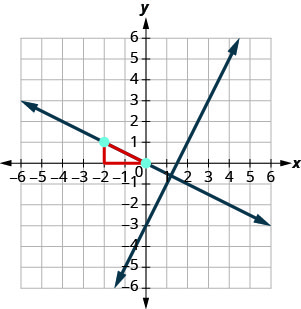
Do the lines appear perpendicular? Does the second line pass through $(-2,1)$?

Now, let’s see how to do this algebraically. We can use either the slope–intercept form or the point–slope form to find the equation of a line. In this example, we know one point, and can find the slope, so we will use the point–slope form.

Example 8

Find an equation of a line perpendicular to $y=2x-3$ that contains the point $(-2,1)$. Write the equation in slope–intercept form.

Solution

$This figure is a table that has three columns and four rows. The first column is a header column, and it contains the names and numbers of each step. The second column contains further written instructions. The third column contains math. In the first row of the table, the first cell on the left reads: “Step 1. Find the slope of the given line.” The second cell reads: “The line is in slope-intercept form. y equals 2x minus 3.” The third cell contains the slope of a line, defined as m equals 2.$
$In the second row, the first cell reads “Step 2. Find the slope of the perpendicular line.” The second cell reads “The slopes of perpendicular lines are negative reciprocals.” The third cell contains m equals negative one half.$
$In the third row, the first cell reads “Step 3. Identify the point.” The second cell reads “The given point is (negative 2, 1).” The third cell contains the ordered pair (negative 2, 1) with a superscript x subscript 1 above negative 2 and a superscript y subscript 1 above 1.$
$In the fourth row, the first cell says “Step 4. Substitute the values into the point-slope form.” The second cell says, “Simplify.” The third cell shows this work, ending with y - 1 = - 1/2 x - 1.$
$In the fifth row, the first cell says “Step 5. Write the equation in slope-intercept form.” The second cell is blank. The third cell contains y equals negative 1 half x.$

Try It 8

Find an equation of a line perpendicular to the line $y=\frac{1}{2}x-3$ that contains the point $(6,4)$.

Answer: b. $y=-2x+16$

FIND AN EQUATION OF A LINE PERPENDICULAR TO A GIVEN LINE.

Find the slope of the given line.
Find the slope of the perpendicular line.
Identify the point.
Substitute the values into the point–slope form, $y-y_{1}=m(x-x_{1})$.
Write the equation in slope–intercept form.

Suppose we want to find a line that is perpendicular to $x=5$ and contains the point $(3, -2)$. The graph shows us the line $x=5$ and the point $(3,-2)$.

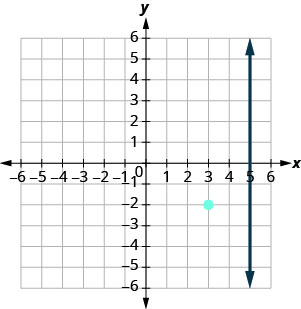
The graph shows the x y-coordinate plane. The x and y-axes each run from negative 7 to 7. The line whose equation is x equals 5 intercepts the x-axis at (5, 0) and runs parallel to the y-axis. Elsewhere on the graph, the point (3, negative 2) is plotted.

We know every line perpendicular to a vertical line is horizontal, so we will sketch the horizontal line through $(3,-2)$.

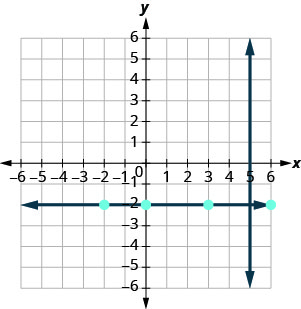
Do the lines appear perpendicular?

If we examine a few points on this horizontal line, we notice that they all have $y$-coordinates of -2. Therefore, the equation of the line perpendicular to the vertical line $x=5$ is $y=-2$.

Example 9

Find an equation of a line that is perpendicular to $y=-4$ that contains the point $(-4,2)$. Write the equation in slope–intercept form.

Solution

The line $y=-4$ is horizontal. Any line perpendicular to it must be vertical, in the form $x=a$. Since the perpendicular line is vertical and passes through $(-4,2)$, every point on it has an $x$-coordinate of -4. The equation of the perpendicular line is $x=-4$. You may want to sketch the lines. Do they appear perpendicular?

Try It 9

Find an equation of a line that is perpendicular to the line $x=1$ that contains the point $(-5,2)$. Write the equation in slope–intercept form.

Answer: $y=2$