11.2: Solve Quadratic Equations Using the Square Root Property

Learning Objectives

By the end of this section, you will be able to:

• Solve quadratic equations of the form $ax^{2}=k$ using the Square Root Property
• Solve quadratic equations of the form $a(x–h)^{2}=k$ using the Square Root Property

Before you get started, take this readiness quiz.

1. Simplify: $\sqrt{128}$.
   If you missed this problem, review Example 8.13.
2. Simplify: $\sqrt{\frac{32}{5}}$.
   If you missed this problem, review Example 8.50.
3. Factor: $9 x^{2}-12 x+4$.
   If you missed this problem, review Example 6.23.

A quadratic equation is an equation of the form $a x^{2}+b x+c=0$, where $a≠0$. Quadratic equations differ from linear equations by including a quadratic term with the variable raised to the second power of the form $ax^{2}$. We use different methods to solve quadratic equations than linear equations, because just adding, subtracting, multiplying, and dividing terms will not isolate the variable.

We have seen that some quadratic equations can be solved by factoring. In this chapter, we will learn three other methods to use in case a quadratic equation cannot be factored.

Solve Quadratic Equations of the Form $ax^{2}=k$ using the Square Root Property

We have already solved some quadratic equations by factoring. Let’s review how we used factoring to solve the quadratic equation $x^{2}=9$.

$x^{2}=9$

Put the equation in standard form.

$x^{2}-9=0$

Factor the difference of squares.

$(x-3)(x+3)=0$

Use the Zero Produce Property.

$x-3=0 \quad x-3=0$

Solve each equation.

$x=3 \quad x=-3$

We can easily use factoring to find the solutions of similar equations, like $x^{2}=16$ and $x^{2}=25$, because $16$ and $25$ are perfect squares. In each case, we would get two solutions, $x=4, x=-4$ and $x=5, x=-5$

But what happens when we have an equation like $x^{2}=7$? Since $7$ is not a perfect square, we cannot solve the equation by factoring.

Previously we learned that since $169$ is the square of $13$, we can also say that $13$ is a square root of $169$. Also, $(-13)^{2}=169$, so $−13$ is also a square root of $169$. Therefore, both $13$ and $−13$ are square roots of $169$. So, every positive number has two square roots—one positive and one negative. We earlier defined the square root of a number in this way:

If $n^{2}=m$, then $n$ is a square root of $m$.

Since these equations are all of the form $x^{2}=k$, the square root definition tells us the solutions are the two square roots of $k$. This leads to the Square Root Property.

Definition $\PageIndex{1}$

Square Root Property

If $x^{2}=k$, then

$x=\sqrt{k} \quad$ or $\quad x=-\sqrt{k} \quad$ or $\quad x=\pm \sqrt{k}$

Notice that the Square Root Property gives two solutions to an equation of the form $x^{2}=k$, the principal square root of $k$ and its opposite. We could also write the solution as $x=\pm \sqrt{k}$. We read this as $x$ equals positive or negative the square root of $k$.

Now we will solve the equation $x^{2}=9$ again, this time using the Square Root Property.

$\begin{aligned} &x^{2} =9 \\ \text { Use the Square Root Property. } \quad& x=\pm \sqrt{9} \\& x =\pm 3 \end{aligned}$

So $x=3$ or $x=-3$

What happens when the constant is not a perfect square? Let’s use the Square Root Property to solve the equation $x^{2}=7$.

$x^{2}=7$

Use the Square Root Property. $x=\sqrt{7}, \quad x=-\sqrt{7}$

We cannot simplify $\sqrt{7}$, so we leave the answer as a radical.

Example $\PageIndex{1}$ How to Solve a Quadratic Equation of the form $ax^{2}-k$ Using the Square Root Property

Solve: $x^{2}-50=0$.

Solution:

Table 9.1.1

Step 1: Isolate the quadratic term and make its coefficient one.	Add $50$ to both sides to get $x^{2}$ by itself.	$\begin{aligned} x^{2}-50 &=0 \\ x^{2} &=50 \end{aligned}$
Step 2: Use the Square Root Property.	Remember to write the $\pm$ symbol.	$x=\pm \sqrt{50}$
Step 3: Simplify the radical.	Rewrite to show two solutions.	$\begin{array}{l}{x=\pm \sqrt{25} \cdot \sqrt{2}} \\ {x=\pm 5 \sqrt{2}} \\ {}x=5\sqrt{2}, \:x=-5\sqrt{2}\end{array}$
Step 4: Check the solutions.	Substitute in $x=5 \sqrt{2}$ and $x=-5 \sqrt{2}$	$\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}$ $\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{-5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}$

Exercise $\PageIndex{1}$

Solve: $x^{2}-48=0$.

Answer

$x=4 \sqrt{3}, x=-4 \sqrt{3}$

Exercise $\PageIndex{2}$

Solve: $y^{2}-27=0$.

Answer

$y=3 \sqrt{3}, y=-3 \sqrt{3}$

The steps to take to use the Square Root Property to solve a quadratic equation are listed here.

Solve a Quadratic Equation Using the Square Root Property

1. Isolate the quadratic term and make its coefficient one.
2. Use Square Root Property.
3. Simplify the radical.
4. Check the solutions.

In order to use the Square Root Property, the coefficient of the variable term must equal one. In the next example, we must divide both sides of the equation by the coefficient $3$ before using the Square Root Property.

Example $\PageIndex{2}$

Solve: $3 z^{2}=108$.

Solution:

Table 9.1.2

	$3 z^{2}=108$
The quadratic term is isolated. Divide by $3$ to make its coefficient $1$.	$\frac{3 z^{2}}{3}=\frac{108}{3}$
Simplify.	$z^{2}=36$
Use the Square Root Property.	$z=\pm \sqrt{36}$
Simplify the radical.	$z=\pm 6$
Rewrite to show two solutions.	$z=6, \quad z=-6$
Check the solutions: Figure 9.1.1

Exercise $\PageIndex{3}$

Solve: $2x^{2}=98$.

Answer

$x=7, x=-7$

Exercise $\PageIndex{4}$

Solve: $5m^{2}=80$.

Answer

$m=4, m=-4$

The Square Root Property states ‘If $x^{2}=k$,’ What will happen if $k<0$? This will be the case in the next example.

Example $\PageIndex{3}$

Solve: $x^{2}+72=0$.

Solution:

Table 9.1.3

	$x^{2}+72=0$
Isolate the quadratic term.	$x^{2}=-72$
Use the Square Root Property.	$x=\pm \sqrt{-72}$
Simplify using complex numbers.	$x=\pm \sqrt{72} i$
Simplify the radical.	$x=\pm 6 \sqrt{2} i$
Rewrite to show two solutions	$x=6 \sqrt{2} i, x=-6 \sqrt{2} i$
Check the solutions: $\begin{array}{r}{x^{2}+72=0}  \\ {(\color{red}{6 \sqrt{2}i}\color{black}{)}^{2}+72 \stackrel{?}{=} 0}  \\ {\color{red}{(6)^2 \cdot (\sqrt{2})^2\cdot i^2}\color{black}+72 \stackrel{?}{=} 0}  \\ {36 \cdot 2\cdot(-1)+72 \stackrel{?}{=} 0}  \\ {0=0}\Large\color{\green}{\checkmark}\end{array}$	$\begin{array}{r}{x^{2}+72=0}  \\ {(\color{red}{-6 \sqrt{2}i}\color{black}{)}^{2}+72 \stackrel{?}{=} 0}  \\ {\color{red}{(-6)^2 \cdot (\sqrt{2})^2\cdot i^2}\color{black}+72 \stackrel{?}{=} 0}  \\ {36 \cdot 2\cdot(-1)+72 \stackrel{?}{=} 0}  \\ {0=0}\Large\color{\green}{\checkmark}\end{array}$

Exercise $\PageIndex{5}$

Solve: $c^{2}+12=0$.

Answer

$c=2 \sqrt{3} i, \quad c=-2 \sqrt{3} i$

Exercise $\PageIndex{6}$

Solve: $q^{2}+24=0$.

Answer

$c=2 \sqrt{6} i, \quad c=-2 \sqrt{6} i$

Our method also works when fractions occur in the equation, we solve as any equation with fractions. In the next example, we first isolate the quadratic term, and then make the coefficient equal to one.

Example $\PageIndex{4}$

Solve: $\frac{2}{3} u^{2}+5=17$.

Solution:

Table 9.1.4

	$\frac{2}{3} u^{2}+5=17$
Isolate the quadratic term.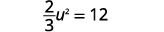
Multiply by $\frac{3}{2}$ to make the coefficient $1$.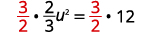
Simplify.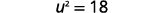
Use the Square Root Property.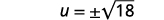
Simplify the radical.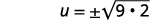
Simplify.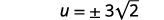
Rewrite to show two solutions.
Check: $\begin{array}{r}{\frac{2}{3}u^{2}+5=17}  \\ {\frac{2}{3}(\color{red}{3 \sqrt{2}}\color{black}{)}^{2}+5 \stackrel{?}{=}17}  \\ {\frac{2}{3}\cdot 18+5 \stackrel{?}{=} 17}  \\ {12+5 \stackrel{?}{=} 17}  \\ {17=17}\Large\color{\green}{\checkmark}\end{array}$	$\begin{array}{r}{\frac{2}{3}u^{2}+5=17}  \\ {\frac{2}{3}(\color{red}{-3 \sqrt{2}}\color{black}{)}^{2}+5 \stackrel{?}{=}17}  \\ {\frac{2}{3}\cdot 18+5 \stackrel{?}{=} 17}  \\ {12+5 \stackrel{?}{=} 17}  \\ {17=17}\Large\color{\green}{\checkmark}\end{array}$

Exercise $\PageIndex{7}$

Solve: $\frac{1}{2} x^{2}+4=24$.

Answer

$x=2 \sqrt{10}, x=-2 \sqrt{10}$

Exercise $\PageIndex{8}$

Solve: $\frac{3}{4} y^{2}-3=18$.

Answer

$y=2 \sqrt{7}, y=-2 \sqrt{7}$

The solutions to some equations may have fractions inside the radicals. When this happens, we must rationalize the denominator.

Example $\PageIndex{5}$

Solve: $2 x^{2}-8=41$.

Solution:

Table 9.1.5

Isolate the quadratic term.
Divide by $2$ to make the coefficient $1$.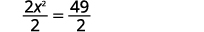
Simplify.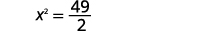
Use the Square Root Property.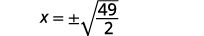
Rewrite the radical as a fraction of square roots.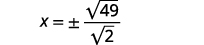
Rationalize the denominator.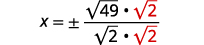
Simplify.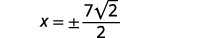
Rewrite to show two solutions.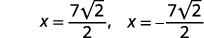
Check: We leave te check for you.

Exercise $\PageIndex{9}$

Solve: $5 r^{2}-2=34$.

Answer

$r=\frac{6 \sqrt{5}}{5}, \quad r=-\frac{6 \sqrt{5}}{5}$

Exercise $\PageIndex{10}$

Solve: $3 t^{2}+6=70$.

Answer

$t=\frac{8 \sqrt{3}}{3}, \quad t=-\frac{8 \sqrt{3}}{3}$

Solve Quadratic Equation of the Form $a(x-h)^{2}=k$ Using the Square Root Property

We can use the Square Root Property to solve an equation of the form $a(x-h)^{2}=k$ as well. Notice that the quadratic term, $x$, in the original form $ax^{2}=k$ is replaced with $(x-h)$.

Figure 9.1.20

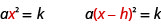
The first step, like before, is to isolate the term that has the variable squared. In this case, a binomial is being squared. Once the binomial is isolated, by dividing each side by the coefficient of $a$, then the Square Root Property can be used on $(x-h)^{2}$.

Example $\PageIndex{6}$

Solve: $4(y-7)^{2}=48$.

Solution:

Table 9.1.6

	$4(y-7)^{2}=48$
Divide both sides by the coefficient $4$.	$(y-7)^{2}=12$
Use the Square Root Property on the binomial.	$y-7=\pm \sqrt{12}$
Simplify the radical.	$y-7=\pm 2 \sqrt{3}$
Solve for $y$.	$y=7 \pm 2 \sqrt{3}$
Rewrite to show two solutions.	$y=7+2 \sqrt{3}$ $y=7-2 \sqrt{3}$
Check: Figure 9.1.21

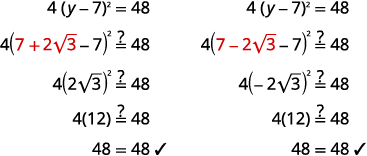
Exercise $\PageIndex{11}$

Solve: $3(a-3)^{2}=54$.

Answer

$a=3+3 \sqrt{2}, \quad a=3-3 \sqrt{2}$

Exercise $\PageIndex{12}$

Solve: $2(b+2)^{2}=80$.

Answer

$b=-2+2 \sqrt{10}, \quad b=-2-2 \sqrt{10}$

Remember when we take the square root of a fraction, we can take the square root of the numerator and denominator separately.

Example $\PageIndex{7}$

Solve: $\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}$.

Solution:

$\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}$

Use the Square Root Property.

$x-\frac{1}{3}=\pm \sqrt{\frac{5}{9}}$

Rewrite the radical as a fraction of square roots.

$x-\frac{1}{3}=\pm \frac{\sqrt{5}}{\sqrt{9}}$

Simplify the radical.

$x-\frac{1}{3}=\pm \frac{\sqrt{5}}{3}$

Solve for $x$.

$x=\frac{1}{3} \pm \frac{\sqrt{5}}{3}$

Rewrite to show two solutions.

$x=\frac{1}{3}+\frac{\sqrt{5}}{3}, x=\frac{1}{3}-\frac{\sqrt{5}}{3}$

Check:

We leave the check for you.

Exercise $\PageIndex{13}$

Solve: $\left(x-\frac{1}{2}\right)^{2}=\frac{5}{4}$.

Answer

$x=\frac{1}{2}+\frac{\sqrt{5}}{2}, x=\frac{1}{2}-\frac{\sqrt{5}}{2}$

Exercise $\PageIndex{14}$

Solve: $\left(y+\frac{3}{4}\right)^{2}=\frac{7}{16}$.

Answer

$y=-\frac{3}{4}+\frac{\sqrt{7}}{4}, y=-\frac{3}{4}-\frac{\sqrt{7}}{4}$

We will start the solution to the next example by isolating the binomial term.

Example $\PageIndex{8}$

Solve: $2(x-2)^{2}+3=57$.

Solution:

$2(x-2)^{2}+3=57$

Subtract $3$ from both sides to isolate the binomial term.

$2(x-2)^{2}=54$

Divide both sides by $2$.

$(x-2)^{2}=27$

Use the Square Root Property.

$x-2=\pm \sqrt{27}$

Simplify the radical.

$x-2=\pm 3 \sqrt{3}$

Solve for $x$.

$x=2 \pm 3 \sqrt{3}$

Rewrite to show two solutions.

$x=2+3 \sqrt{3}, x=2-3 \sqrt{3}$

Check:

We leave the check for you.

Exercise $\PageIndex{15}$

Solve: $5(a-5)^{2}+4=104$.

Answer

$a=5+2 \sqrt{5}, a=5-2 \sqrt{5}$

Exercise $\PageIndex{16}$

Solve: $3(b+3)^{2}-8=88$.

Answer

$b=-3+4 \sqrt{2}, \quad b=-3-4 \sqrt{2}$

Sometimes the solutions are complex numbers.

Example $\PageIndex{9}$

Solve: $(2 x-3)^{2}=-12$.

Solution:

$(2 x-3)^{2}=-12$

Use the Square Root Property.

$2 x-3=\pm \sqrt{-12}$

Simplify the radical.

$2 x-3=\pm 2 \sqrt{3} i$

Add $3$ to both sides.

$2 x=3 \pm 2 \sqrt{3} i$

Divide both sides by $2$.

$x=\frac{3 \pm 2 \sqrt{3 i}}{2}$

Rewrite in standard form.

$x=\frac{3}{2} \pm \frac{2 \sqrt{3} i}{2}$

Simplify.

$x=\frac{3}{2} \pm \sqrt{3} i$

Rewrite to show two solutions.

$x=\frac{3}{2}+\sqrt{3} i, x=\frac{3}{2}-\sqrt{3} i$

Check:

We leave the check for you.

Exercise $\PageIndex{17}$

Solve: $(3 r+4)^{2}=-8$.

Answer

$r=-\frac{4}{3}+\frac{2 \sqrt{2} i}{3}, r=-\frac{4}{3}-\frac{2 \sqrt{2} i}{3}$

Exercise $\PageIndex{18}$

Solve: $(2 t-8)^{2}=-10$.

Answer

$t=4+\frac{\sqrt{10} i}{2}, t=4-\frac{\sqrt{10 i}}{2}$

The left sides of the equations in the next two examples do not seem to be of the form $a(x-h)^{2}$. But they are perfect square trinomials, so we will factor to put them in the form we need.

Example $\PageIndex{10}$

Solve: $4 n^{2}+4 n+1=16$.

Solution:

We notice the left side of the equation is a perfect square trinomial. We will factor it first.

Table 9.1.7

	$4 n^{2}+4 n+1=16$
Factor the perfect square trinomial.	$(2 n+1)^{2}=16$
Use the Square Root Property.	$2 n+1=\pm \sqrt{16}$
Simplify the radical.	$2 n+1=\pm 4$
Solve for $n$.	$2 n=-1 \pm 4$
Divide each side by $2$.	$\begin{aligned} \frac{2 n}{2} &=\frac{-1 \pm 4}{2} \\ n &=\frac{-1 \pm 4}{2} \end{aligned}$
Rewrite to show two solutions.	$n=\frac{-1+4}{2}, n=\frac{-1-4}{2}$
Simplify each equation.	$n=\frac{3}{2}, \quad n=-\frac{5}{2}$
Check: Figure 9.1.22

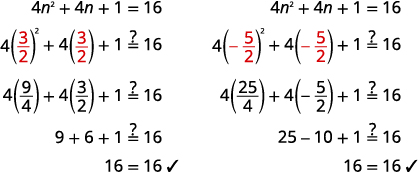
Exercise $\PageIndex{19}$

Solve: $9 m^{2}-12 m+4=25$.

Answer

$m=\frac{7}{3}, \quad m=-1$

Exercise $\PageIndex{20}$

Solve: $16 n^{2}+40 n+25=4$.

Answer

$n=-\frac{3}{4}, \quad n=-\frac{7}{4}$

Access this online resource for additional instruction and practice with using the Square Root Property to solve quadratic equations.

• Solving Quadratic Equations: The Square Root Property
• Using the Square Root Property to Solve Quadratic Equations

Key Concepts

• Square Root Property
  • If $x^{2}=k$, then $x=\sqrt{k}$ or $x=-\sqrt{k}$or $x=\pm \sqrt{k}$
  How to solve a quadratic equation using the square root property.
  1. Isolate the quadratic term and make its coefficient one.
  2. Use Square Root Property.
  3. Simplify the radical.
  4. Check the solutions.