12.3E: Exercises
- Last updated
- Aug 24, 2020
- Save as PDF
- Page ID
- 50014
( \newcommand{\kernel}{\mathrm{null}\,}\)
Practice Makes Perfect
Exercise 12.3E.17 Graph Exponential Functions
In the following exercises, graph each exponential function.
- f(x)=2x
- g(x)=3x
- f(x)=6x
- g(x)=7x
- f(x)=(1.5)x
- g(x)=(2.5)x
- f(x)=(12)x
- g(x)=(13)x
- f(x)=(16)x
- g(x)=(17)x
- f(x)=(0.4)x
- g(x)=(0.6)x
- Answer
-
1.
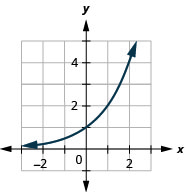
Figure 10.2.22 3.
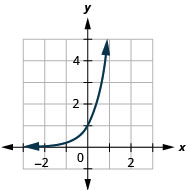
Figure 10.2.23 5.
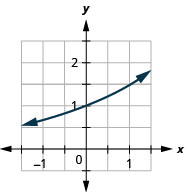
Figure 10.2.24 7.
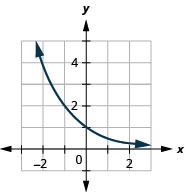
Figure 10.2.25 9.
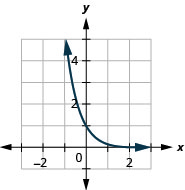
Figure 10.2.26 11.
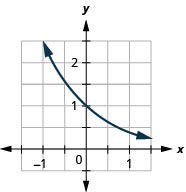
Figure 10.2.27
Exercise 12.3E.18 Graph Exponential Functions
In the following exercises, graph each function in the same coordinate system.
- f(x)=4x,g(x)=4x−1
- f(x)=3x,g(x)=3x−1
- f(x)=2x,g(x)=2x−2
- f(x)=2x,g(x)=2x+2
- f(x)=3x,g(x)=3x+2
- f(x)=4x,g(x)=4x+2
- f(x)=2x,g(x)=2x+1
- f(x)=2x,g(x)=2x−1
- Answer
-
1.
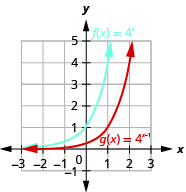
Figure 10.2.28 3.
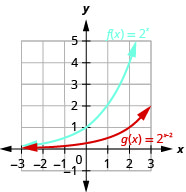
Figure 10.2.29 5.
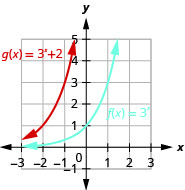
Figure 10.2.30 7.
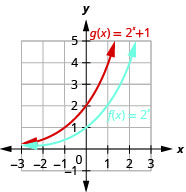
Figure 10.2.31
Exercise 12.3E.19 Graph Exponential Functions
In the following exercises, graph each exponential function.
- f(x)=3x+2
- f(x)=3x−2
- f(x)=2x+3
- f(x)=2x−3
- f(x)=(12)x−4
- f(x)=(12)x−3
- f(x)=ex+1
- f(x)=ex−2
- f(x)=−2x
- f(x)=2−x−1−1
- Answer
-
1.
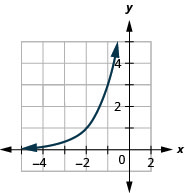
Figure 10.2.32 3.
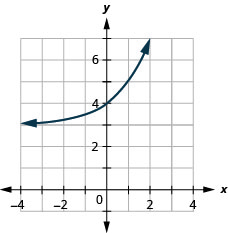
Figure 10.2.33 5.
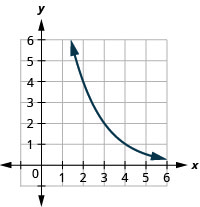
Figure 10.2.34 7.
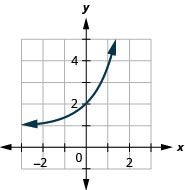
Figure 10.2.35 9.
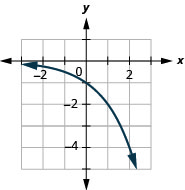
Figure 10.2.36
Exercise 12.3E.20 Solve Exponential Equations
In the following exercises, solve each equation.
- 23x−8=16
- 22x−3=32
- 3x+3=9
- 3x2=81
- 4x2=4
- 4x=32
- 4x+2=64
- 4x+3=16
- 2x2+2x=12
- 3x2−2x=13
- e3x⋅e4=e10
- e2x⋅e3=e9
- ex2e2=ex
- ex2e3=e2x
- Answer
-
1. x=4
3. x=−1
5. x=−1,x=1
7. x=1
9. x=−1
11. x=2
13. x=−1,x=2
Exercise 12.3E.21 Solve Exponential Equations
In the following exercises, match the graphs to one of the following functions:
- 2x
- 2x+1
- 2x−1
- 2x+2
- 2x−2
- 3x
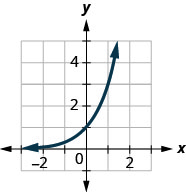
Figure 10.2.37
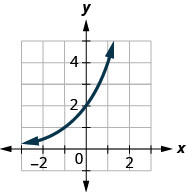
Figure 10.2.38
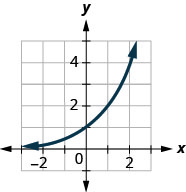
Figure 10.2.39
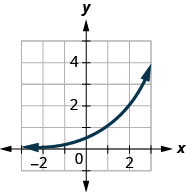
Figure 10.2.40
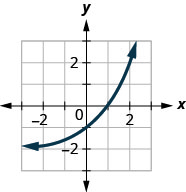
Figure 10.2.41
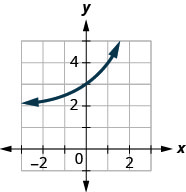
Figure 10.2.42
- Answer
-
1. f
3. a
5. e
Exercise 12.3E.22 Use Exponential Models in Applications
In the following exercises, use an exponential model to solve.
- Edgar accumulated $5,000 in credit card debt. If the interest rate is 20% per year, and he does not make any payments for 2 years, how much will he owe on this debt in 2 years by each method of compounding?
- compound quarterly
- compound monthly
- compound continuously
- Cynthia invested $12,000 in a savings account. If the interest rate is 6%, how much will be in the account in 10 years by each method of compounding?
- compound quarterly
- compound monthly
- compound continuously
- Rochelle deposits $5,000 in an IRA. What will be the value of her investment in 25 years if the investment is earning 8% per year and is compounded continuously?
- Nazerhy deposits $8,000 in a certificate of deposit. The annual interest rate is 6% and the interest will be compounded quarterly. How much will the certificate be worth in 10 years?
- A researcher at the Center for Disease Control and Prevention is studying the growth of a bacteria. He starts his experiment with 100 of the bacteria that grows at a rate of 6% per hour. He will check on the bacteria every 8 hours. How many bacteria will he find in 8 hours?
- A biologist is observing the growth pattern of a virus. She starts with 50 of the virus that grows at a rate of 20% per hour. She will check on the virus in 24 hours. How many viruses will she find?
- In the last ten years the population of Indonesia has grown at a rate of 1.12% per year to 258,316,051. If this rate continues, what will be the population in 10 more years?
- In the last ten years the population of Brazil has grown at a rate of 0.9% per year to 205,823,665. If this rate continues, what will be the population in 10 more years?
- Answer
-
1.
- $7,387.28
- $7,434.57
- $7,459.12
3. $36,945.28
5. 223 bacteria
7. 288,929,825
Exercise 12.3E.23 Writing Exercises
- Explain how you can distinguish between exponential functions and polynomial functions.
- Compare and contrast the graphs of y=x2 and y=2x.
- What happens to an exponential function as the values of x decreases? Will the graph ever cross the x-axis? Explain.
- Answer
-
1. Answers will vary
3. Answers will vary
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. After reviewing this checklist, what will you do to become confident for all objectives?

