12.4E: Exercises
- Page ID
- 50016
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Section 10.3 Exercises
Practice Makes Perfect
In the following exercises, convert from exponential to logarithmic form.
- \(4^{2}=16\)
- \(2^{5}=32\)
- \(3^{3}=27\)
- \(5^{3}=125\)
- \(10^{3}=1000\)
- \(10^{-2}=\frac{1}{100}\)
- \(x^{\frac{1}{2}}=\sqrt{3}\)
- \(x^{\frac{1}{3}}=\sqrt[3]{6}\)
- \(32^{x}=\sqrt[4]{32}\)
- \(17^{x}=\sqrt[5]{17}\)
- \(\left(\frac{1}{4}\right)^{2}=\frac{1}{16}\)
- \(\left(\frac{1}{3}\right)^{4}=\frac{1}{81}\)
- \(3^{-2}=\frac{1}{9}\)
- \(4^{-3}=\frac{1}{64}\)
- \(e^{x}=6\)
- \(e^{3}=x\)
- Answer
-
2. \(\log _{2} 32=5\)
4. \(\log _{5} 125=3\)
6. \(\log \frac{1}{100}=-2\)
8. \(\log _{x} \sqrt[3]{6}=\frac{1}{3}\)
10. \(\log _{17} \sqrt[5]{17}=x\)
12. \(\log _{\frac{1}{3}} \frac{1}{81}=4\)
14. \(\log _{4} \frac{1}{64}=-3\)
16. \(\ln x=3\)
In the following exercises, convert each logarithmic equation to exponential form.
- \(3=\log _{4} 64\)
- \(6=\log _{2} 64\)
- \(4=\log _{x} 81\)
- \(5=\log _{x} 32\)
- \(0=\log _{12} 1\)
- \(0=\log _{7} 1\)
- \(1=\log _{3} 3\)
- \(1=\log _{9} 9\)
- \(-4=\log _{10} \frac{1}{10,000}\)
- \(3=\log _{10} 1,000\)
- \(5=\log _{e} x\)
- \(x=\log _{e} 43\)
- Answer
-
2. \(64=2^{6}\)
4. \(32=x^{5}\)
6. \(1=7^{0}\)
8. \(9=9^{1}\)
10. \(1,000=10^{3}\)
12. \(43=e^{x}\)
In the following exercises, find the value of \(x\) in each logarithmic equation.
- \(\log _{x} 49=2\)
- \(\log _{x} 121=2\)
- \(\log _{x} 27=3\)
- \(\log _{x} 64=3\)
- \(\log _{3} x=4\)
- \(\log _{5} x=3\)
- \(\log _{2} x=-6\)
- \(\log _{3} x=-5\)
- \(\log _{\frac{1}{4}} \frac{1}{16}=x\)
- \(\log _{\frac{1}{3}} \frac{1}{9}=x\)
- \(\log _{\frac{1}{4}} 64=x\)
- \(\log _{\frac{1}{9}} 81=x\)
- Answer
-
2. \(x=11\)
4. \(x=4\)
6. \(x=125\)
8. \(x=\frac{1}{243}\)
10. \(x=2\)
12. \(x=-2\)
In the following exercises, find the exact value of each logarithm without using a calculator.
- \(\log _{7} 49\)
- \(\log _{6} 36\)
- \(\log _{4} 1\)
- \(\log _{5} 1\)
- \(\log _{16} 4\)
- \(\log _{27} 3\)
- \(\log _{\frac{1}{2}} 2\)
- \(\log _{\frac{1}{2}} 4\)
- \(\log _{2} \frac{1}{16}\)
- \(\log _{3} \frac{1}{27}\)
- \(\log _{4} \frac{1}{16}\)
- \(\log _{9} \frac{1}{81}\)
- Answer
-
2. \(2\)
4. \(0\)
6. \(\frac{1}{3}\)
8. \(-2\)
10. \(-3\)
12. \(-2\)
In the following exercises, graph each logarithmic function.
- \(y=\log _{2} x\)
- \(y=\log _{4} x\)
- \(y=\log _{6} x\)
- \(y=\log _{7} x\)
- \(y=\log _{1.5} x\)
- \(y=\log _{2.5} x\)
- \(y=\log _{\frac{1}{3}} x\)
- \(y=\log _{\frac{1}{5}} x\)
- \(y=\log _{0.4} x\)
- \(y=\log _{0.6} x\)
- Answer
-
2.
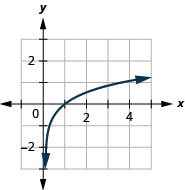
Figure 10.3.19 4.
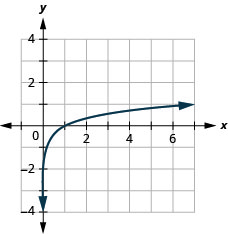
Figure 10.3.20 6.
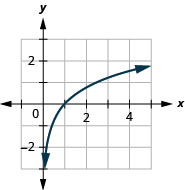
Figure 10.3.21 8.
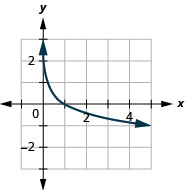
Figure 10.3.22 10.
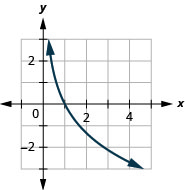
Figure 10.3.23
In the following exercises, solve each logarithmic equation.
- \(\log _{a} 16=2\)
- \(\log _{a} 81=2\)
- \(\log _{a} 8=3\)
- \(\log _{a} 27=3\)
- \(\log _{a} 32=2\)
- \(\log _{a} 24=3\)
- \(\ln x=5\)
- \(\ln x=4\)
- \(\log _{2}(5 x+1)=4\)
- \(\log _{2}(6 x+2)=5\)
- \(\log _{3}(4 x-3)=2\)
- \(\log _{3}(5 x-4)=4\)
- \(\log _{4}(5 x+6)=3\)
- \(\log _{4}(3 x-2)=2\)
- \(\ln e^{4 x}=8\)
- \(\ln e^{2 x}=6\)
- \(\log x^{2}=2\)
- \(\log \left(x^{2}-25\right)=2\)
- \(\log _{2}\left(x^{2}-4\right)=5\)
- \(\log _{3}\left(x^{2}+2\right)=3\)
- Answer
-
2. \(a=9\)
4. \(a=3\)
6. \(a=\sqrt[3]{24}\)
8. \(x=e^{4}\)
10. \(x=5\)
12. \(x=17\)
14. \(x=6\)
16. \(x=3\)
18. \(x=-5 \sqrt{5}, x=5 \sqrt{5}\)
20. \(x=-5, x=5\)
In the following exercises, use a logarithmic model to solve.
- What is the decibel level of normal conversation with intensity \(10^{−6}\) watts per square inch?
- What is the decibel level of a whisper with intensity \(10^{−10}\) watts per square inch?
- What is the decibel level of the noise from a motorcycle with intensity \(10^{−2}\) watts per square inch?
- What is the decibel level of the sound of a garbage disposal with intensity \(10^{−2}\) watts per square inch?
- In 2014, Chile experienced an intense earthquake with a magnitude of \(8.2\) on the Richter scale. In 2010, Haiti also experienced an intense earthquake which measured \(7.0\) on the Richter scale. Compare the intensities of the two earthquakes.
- The Los Angeles area experiences many earthquakes. In 1994, the Northridge earthquake measured magnitude of \(6.7\) on the Richter scale. In 2014, Los Angeles also experienced an earthquake which measured \(5.1\) on the Richter scale. Compare the intensities of the two earthquakes.
- Answer
-
2. A whisper has a decibel level of \(20\) dB.
4. The sound of a garbage disposal has a decibel level of \(100\) dB.
6. The intensity of the 1994 Northridge earthquake in the Los Angeles area was about \(40\) times the intensity of the 2014 earthquake.
- Explain how to change an equation from logarithmic form to exponential form.
- Explain the difference between common logarithms and natural logarithms.
- Explain why \(\log _{a} a^{x}=x\).
- Explain how to find the \(\log _{7} 32\) on your calculator.
- Answer
-
2. Answers may vary
4. Answers may vary
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. After reviewing this checklist, what will you do to become confident for all objectives?