1.1: Functions and Function Notation
For the exercises 1-4, determine whether the relation is a function.
1) \(\{(a,b),(c,d),(e,d)\}\)
- Answer
-
function
2) \(\{(5,2),(6,1),(6,2),(4,8)\}\)
3) \(y^2+4=x\), for \(x\) the independent variable and \(y\) the dependent variable
- Answer
-
not a function
4) Is the graph in the Figure below a function?
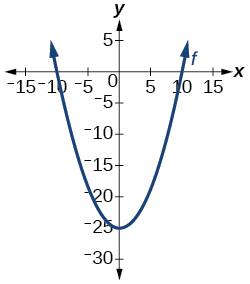
For the exercises 5-6, evaluate the function at the indicated values: \(f(-3); f(2); f(-a); -f(a); f(a+h)\)
5) \(f(x)=-2x^2+3x\)
- Answer
-
\(f(-3)=-27; f(2)=-2;f(-a)=-2a^2-3a;-f(a)=2a^2-3a;f(a+h)=-2a^2+3a-4ah+3h-2h^2\)
6) \(f(x)=2|3x-1|\)
For the exercises 7-8, determine whether the functions are one-to-one.
7) \(f(x)=-3 x+5\)
- Answer
-
one-to-one
8) \(f(x)=|x-3|\)
For the exercises 9-11, use the vertical line test to determine if the relation whose graph is provided is a function.
9)
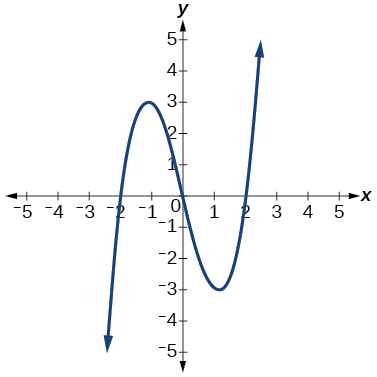
- Answer
-
function
10)
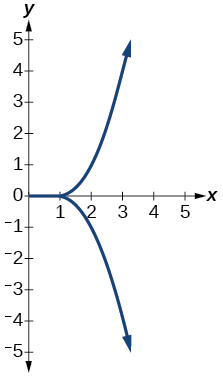
11)
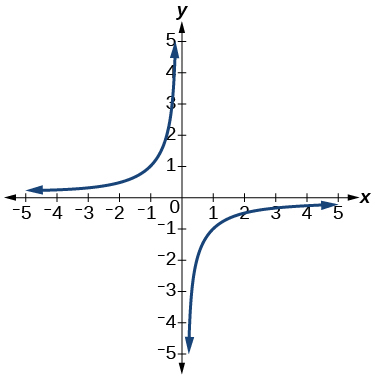
- Answer
-
function
For the exercises 12-13, graph the functions.
12) \(f(x)=|x+1|\)
13) \(f(x)=x^{2}-2\)
- Answer
-
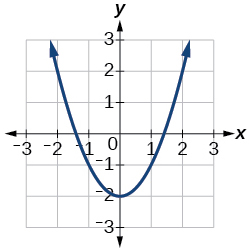
For the exercises 14-17, use the Figure below to approximate the values.
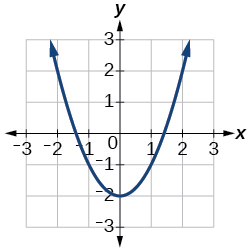
14) \(f(2)\)
15) \(f(-2)\)
- Answer
-
\(2\)
16) If \(f(x)=-2\), then solve for \(x\)
17) If \(f(x)=1\), then solve for \(x\)
- Answer
-
\(x=-1.8\) or \(x=1.8\)
For the exercises 18-19, use the function \(h(t)=-16 t^{2}+80t\) to find the values.
18) \(\dfrac{h(2)-h(1)}{2-1}\)
19) \(\dfrac{h(a)-h(1)}{a-1}\)
- Answer
-
\(\dfrac{-64+80 a-16 a^{2}}{-1+a}=-16 a+64\)
1.2: Domain and Range
For the exercises 1-4, find the domain of each function, expressing answers using interval notation.
1) \(f(x)=\dfrac{2}{3 x+2}\)
2) \(f(x)=\frac{x-3}{x^{2}-4 x-12}\)
- Answer
-
\((-\infty,-2) \cup(-2,6) \cup(6, \infty)\)
3)
4) Graph this piecewise function: \(f(x)=\left\{\begin{array}{ll}{x+1} & {x<-2} \\ {-2 x-3} & {x \geq-2}\end{array}\right.\)
- Answer
-
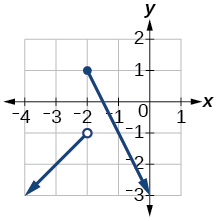
1.3: Rates of Change and Behavior of Graphs
For the exercises 1-3, find the average rate of change of the functions from \(x=1\) to \(x=2\)
1) \(f(x)=4 x-3\)
2) \(f(x)=10 x^{2}+x\)
- Answer
-
\(31\)
3) \(f(x)=-\dfrac{2}{x^{2}}\)
For the exercises 4-6, use the graphs to determine the intervals on which the functions are increasing, decreasing, or constant.
4)
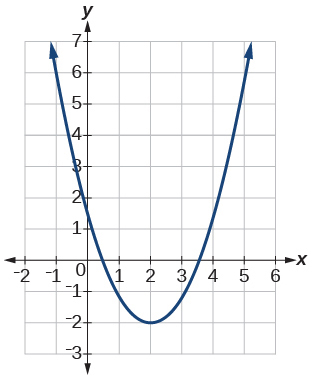
- Answer
-
increasing \((2, \infty)\); decreasing \((-\infty, 2)\)
5)
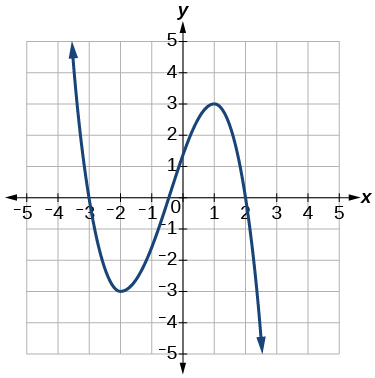
6)
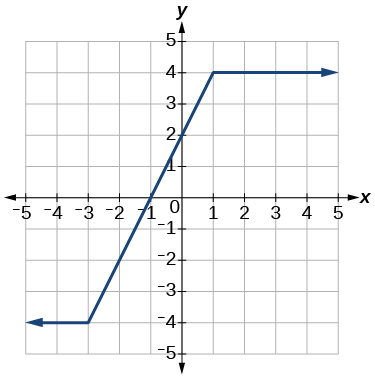
- Answer
-
increasing \((-3,1)\); constant \((-\infty,-3) \cup(1, \infty)\)
7) Find the local minimum of the function graphed in Exercise 4.
8) Find the local extrema for the function graphed in Exercise 5.
- Answer
-
local minimum \((-2,-3)\); local maximum \((1,3)\)
9) For the graph in the Figure in Exercise 10, the domain of the function is \([-3,3]\). The range is \([-10,10]\). Find the absolute minimum of the function on this interval.
10) Find the absolute maximum of the function graphed in the Figure below.
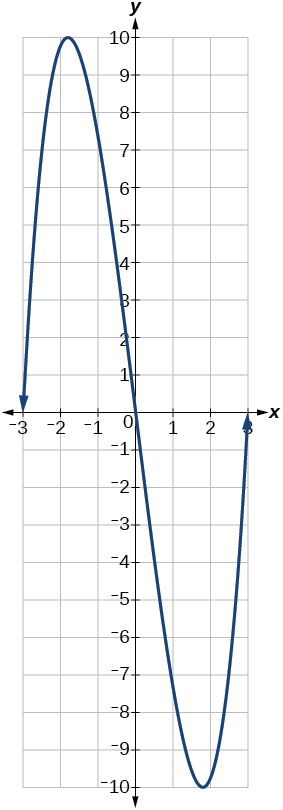
- Answer
-
\((-1.8,10)\)
1.4: Composition of Functions
For the exercises 1-5, find \((f \circ g)(x)\) and \((g \circ f)(x)\) for each pair of functions.
1) \(f(x)=4-x, g(x)=-4x\)
2) \(f(x)=3 x+2, g(x)=5-6x\)
- Answer
-
\((f \circ g)(x)=17-18 x ;(g \circ f)(x)=-7-18x\)
3) \(f(x)=x^{2}+2 x, g(x)=5 x+1\)
4) \(f(x)=\sqrt{x+2}, g(x)=\dfrac{1}{x}\)
- Answer
-
\((f \circ g)(x)=\sqrt{\dfrac{1}{x}+2} ;(g \circ f)(x)=\dfrac{1}{\sqrt{x+2}}\)
5) \(f(x)=\dfrac{x+3}{2}, g(x)=\sqrt{1-x}\)
For the exercises 6-9, find \((f \circ g)\) and the domain for \((f \circ g)(x)\) for each pair of functions.
6) \(f(x)=\frac{x+1}{x+4}, g(x)=\frac{1}{x}\)
- Answer
-
\((f \circ g)(x)=\dfrac{1+x}{1+4 x}, x \neq 0, x \neq-\dfrac{1}{4}\)
7) \(f(x)=\dfrac{1}{x+3}, g(x)=\dfrac{1}{x-9}\)
8) \(f(x)=\dfrac{1}{x}, g(x)=\sqrt{x}\)
- Answer
-
\((f \circ g)(x)=\frac{1}{\sqrt{x}}, x>0\)
9) \(f(x)=\frac{1}{x^{2}-1}, g(x)=\sqrt{x+1}\)
For the exercises 10-11, express each function \(H\) as a composition of two functions \(f\) and \(g\) where \(H(x)=(f \circ g)(x)\)
10) \(H(x)=\sqrt{\frac{2 x-1}{3 x+4}}\)
- Answer
-
sample: \(g(x)=\dfrac{2 x-1}{3 x+4}; f(x)=\sqrt{x}\)
11) \(H(x)=\dfrac{1}{\left(3 x^{2}-4\right)^{-3}}\)
For the exercises 1-8, sketch a graph of the given function.
1) \(f(x)=(x-3)^{2}\)
- Answer
-
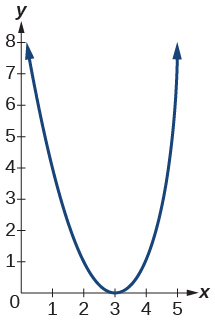
2) \(f(x)=(x+4)^{3}\)
3) \(f(x)=\sqrt{x}+5\)
- Answer
-
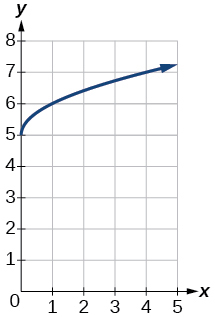
4) \(f(x)=-x^{3}\)
5) \(f(x)=\sqrt[3]{-x}\)
- Answer
-
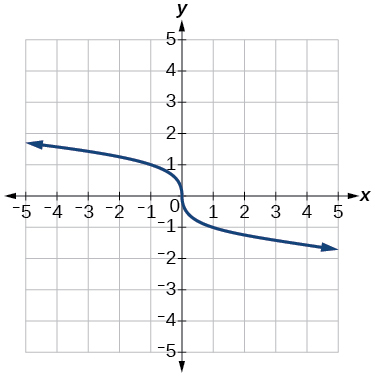
6) \(f(x)=5 \sqrt{-x}-4\)
7) \(f(x)=4[|x-2|-6]\)
- Answer
-
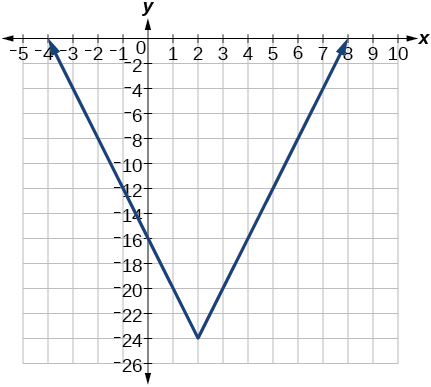
8) \(f(x)=-(x+2)^{2}-1\)
For the exercises 9-10, sketch the graph of the function \(g\) if the graph of the function \(f\) is shown in the Figure below.
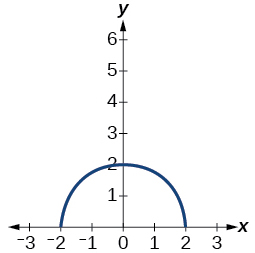
9) \(g(x)=f(x-1)\)
- Answer
-
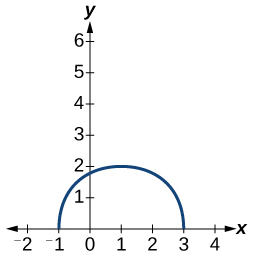
10) \(g(x)=3 f(x)\)
For the exercises 11-12, write the equation for the standard function represented by each of the graphs below.
11)
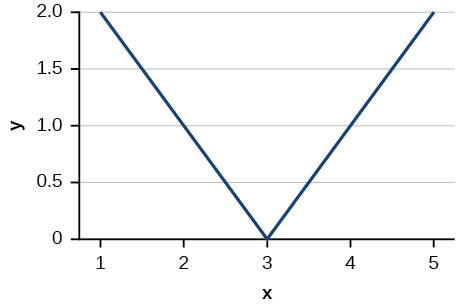
- Answer
-
\(f(x)=|x-3|\)
12)
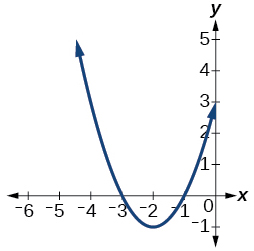
For the exercises 13-15, determine whether each function below is even, odd, or neither.
13) \(f(x)=3 x^{4}\)
- Answer
-
even
14) \(g(x)=\sqrt{x}\)
15) \(h(x)=\frac{1}{x}+3 x\)
- Answer
-
odd
For the exercises 16-18, analyze the graph and determine whether the graphed function is even, odd, or neither.
16)
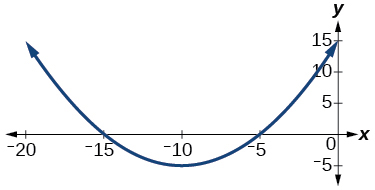
17)
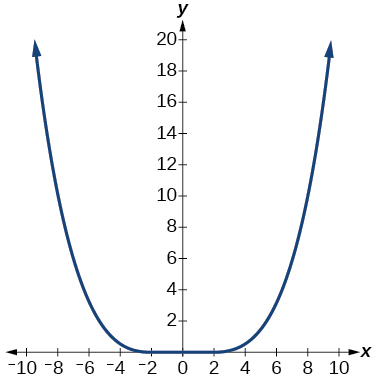
- Answer
-
even
18)
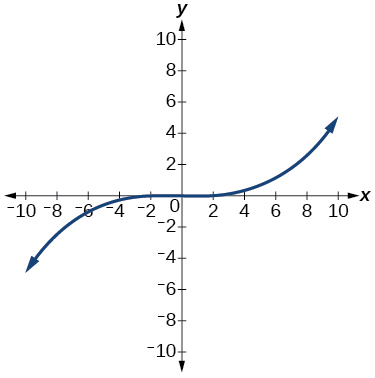
1.6: Absolute Value Functions
For the exercises 1-3, write an equation for the transformation of \(f(x)=|x|\).
1)
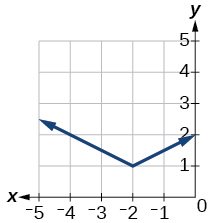
- Answer
-
\(f(x)=\dfrac{1}{2}|x+2|+1\)
2)
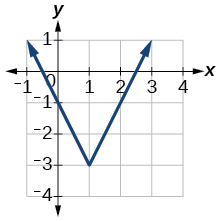
3)
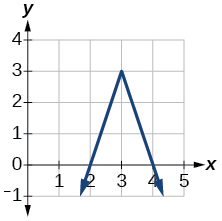
- Answer
-
\(f(x)=-3|x-3|+3\)
For the exercises 4-6, graph the absolute value function.
4) \(f(x)=|x-5|\)
5) \(f(x)=-|x-3|\)
- Answer
-
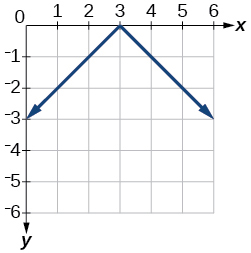
6) \(f(x)=|2 x-4|\)
For the exercises 7-8, solve the absolute value equation.
7) \(|x+4|=18\)
- Answer
-
\(x=-22, x=14\)
8) \(\left|\dfrac{1}{3} x+5\right|=\left|\dfrac{3}{4} x-2\right|\)
For the exercises 9-10, solve the inequality and express the solution using interval notation.
9) \(|3 x-2|<7\)
- Answer
-
\(\left(-\dfrac{5}{3}, 3\right)\)
10) \(\left|\dfrac{1}{3} x-2\right| \leq 7\)
1.7: Inverse Functions
For the exercises 1-2, find \(f^{-1}(x)\) for each function.
1) \(f(x)=9+10 x\)
2) \(f(x)=\dfrac{x}{x+2}\)
- Answer
-
\(f^{-1}(x)=\dfrac{-2 x}{x-1}\)
3) For the following exercise, find a domain on which the function \(f\) is one-to-one and non-decreasing. Write the domain in interval notation. Then find the inverse of \(f\) restricted to that domain. \[f(x)=x^{2}+1\]
4) Given \(f(x)=x^{3}-5\) and \(g(x)=\sqrt[3]{x+5} \) :
- Find \(f(g(x))\) and \(g(f(x))\).
- What does the answer tell us about the relationship between \(f(x)\) and \(g(x) ?\)
- Answer
-
- \(f(g(x))=x\) and \(g(f(x))=x\)
- This tells us that \(f\) and \(g\) are inverse functions
For the exercises 5-8, use a graphing utility to determine whether each function is one-to-one.
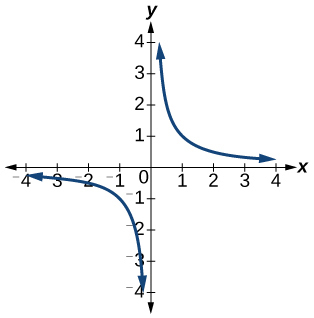
5) \(f(x)=\dfrac{1}{x}\)
- Answer
-
The function is one-to-one.
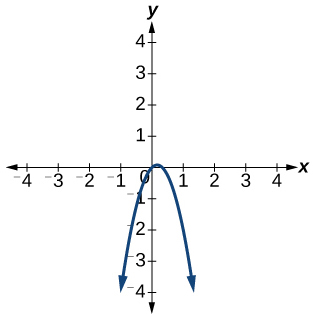
6) \(f(x)=-3 x^{2}+x\)
- Answer
-
The function is not one-to-one.
7) If \(f(5)=2,\) find \(f^{-1}(2)\)
- Answer
-
\(5\)
8) If \(f(1)=4,\) find \(f^{-1}(4)\)
Practice Test
For the exercises 1-2, determine whether each of the following relations is a function.
1) \(y=2 x+8\)
- Answer
-
The relation is a function.
2) \(\{(2,1),(3,2),(-1,1),(0,-2)\}\)
For the exercises 3-4, evaluate the function \(f(x)=-3 x^{2}+2 x\) at the given input.
3) \(f(-2)\)
- Answer
-
\(-16\)
4) \(f(a)\)
5) Show that the function \(f(x)=-2(x-1)^{2}+3\) is not one-to-one.
- Answer
-
The graph is a parabola and the graph fails the horizontal line test.
6) Write the domain of the function \(f(x)=\sqrt{3-x}\) in interval notation.
7) Given \(f(x)=2 x^{2}-5 x,\) find \(f(a+1)-f(1)\)
- Answer
-
\(2 a^{2}-a\)
8) Graph the function \(f(x)=\left\{\begin{array}{ccc}{x+1} & {\text { if }} & {-2<x<3} \\ {-x} & {\text { if }} & {x \geq 3}\end{array}\right.\)
9) Find the average rate of change of the function \(f(x)=3-2 x^{2}+x\) by finding \(\dfrac{f(b)-f(a)}{b-a}\)
- Answer
-
\(-2(a+b)+1\)
For the exercises 10-11, use the functions \(f(x)=3-2 x^{2}+x\) and \(g(x)=\sqrt{x}\) to find the composite functions.
10) \((g \circ f)(x)\)
11) \((g \circ f)(1)\)
- Answer
-
\(\sqrt{2}\)
12) Express \(H(x)=\sqrt[3]{5 x^{2}-3 x}\) a composition of two functions, \(f\) and \(g,\) where \((f \circ g)(x)=H(x)\)
For the exercises 13-14, graph the functions by translating, stretching, and/or compressing a toolkit function.
13) \(f(x)=\sqrt{x+6}-1\)
- Answer
-
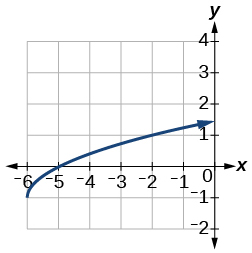
14) \(f(x)=\dfrac{1}{x+2}-1\)
For the exercises 15-17, determine whether the functions are even, odd, or neither.
15) \(f(x)=-\dfrac{5}{x^{2}}+9 x^{6}\)
- Answer
-
even
16) \(f(x)=-\dfrac{5}{x^{3}}+9 x^{5}\)
17) \(f(x)=\dfrac{1}{x}\)
- Answer
-
odd
18) Graph the absolute value function \(f(x)=-2|x-1|+3\).
19) Solve \(|2 x-3|=17\).
- Answer
-
\(x=-7\) and \(x=10\)
20) Solve \(-\left|\dfrac{1}{3} x-3\right| \geq 17\). Express the solution in interval notation.
For the exercises 21-22, find the inverse of the function.
21) \(f(x)=3 x-5\)
- Answer
-
\(f^{-1}(x)=\dfrac{x+5}{3}\)
22) \(f(x)=\dfrac{4}{x+7}\)
For the exercises 23-26, use the graph of \(g\) shown in the Figure below.
23) On what intervals is the function increasing?
- Answer
-
\((-\infty,-1.1)\) and \((1.1, \infty)\)
24) On what intervals is the function decreasing?
25) Approximate the local minimum of the function. Express the answer as an ordered pair.
- Answer
-
\((1.1,-0.9)\)
26) Approximate the local maximum of the function. Express the answer as an ordered pair.
For the exercises 27-29, use the graph of the piecewise function shown in the Figure below.
27) Find \(f(2)\).
- Answer
-
\(f(2)=2\)
28) Find \(f(-2)\).
29) Write an equation for the piecewise function.
- Answer
-
\(f(x)=\left\{\begin{array}{cl}{|x|} & {\text { if } x \leq 2} \\ {3} & {\text { if } x>2}\end{array}\right.\)
For the exercises 30-35, use the values listed in the Table below.
| \(x\) |
\(F(x)\) |
| 0 |
1 |
| 1 |
3 |
| 2 |
5 |
| 3 |
7 |
| 4 |
9 |
| 5 |
11 |
| 6 |
13 |
| 7 |
15 |
| 8 |
17 |
30) Find \(F(6)\).
31) Solve the equation \(F(x)=5\)
- Answer
-
\(x=2\)
32) Is the graph increasing or decreasing on its domain?
33) Is the function represented by the graph one-to-one?
- Answer
-
yes
34) Find \(F^{-1}(15)\).
35) Given \(f(x)=-2 x+11,\) find \(f^{-1}(x)\).
- Answer
-
\(f^{-1}(x)=-\dfrac{x-11}{2}\)
Contributors and Attributions































