2.5E: Exercises for Section 2.4

Last updated

Mar 16, 2023
Save as PDF
- 2.5: The Limit Laws
- 2.6: Limits at Infinity

( \newcommand{\kernel}{\mathrm{null}\,}\)

In exercises 1 - 4, use the limit laws to evaluate each limit. Justify each step by indicating the appropriate limit law(s).

1) $lim_{x \to 0} (4 x^{2} - 2 x + 3)$

Answer:

Use constant multiple law and difference law:

$lim_{x \to 0} (4 x^{2} - 2 x + 3) = 4 lim_{x \to 0} x^{2} - 2 lim_{x \to 0} x + lim_{x \to 0} 3 = 0 + 0 + 3 = 3$

2) $lim_{x \to 1} \frac{x^{3} + 3 x^{2} + 5}{4 - 7 x}$

3) $lim_{x \to - 2} \sqrt{x^{2} - 6 x + 3}$

Answer:: Use root law: $lim_{x \to - 2} \sqrt{x^{2} - 6 x + 3} = \sqrt{lim_{x \to - 2} (x^{2} - 6 x + 3)} = \sqrt{19}$

4) $lim_{x \to - 1} {(9 x + 1)}^{2}$

In exercises 5 - 10, use direct substitution to evaluate the limit of each continuous function.

5) $lim_{x \to 7} x^{2}$

Answer:: $lim_{x \to 7} x^{2} = 49$

6) $lim_{x \to - 2} (4 x^{2} - 1)$

7) $lim_{x \to 0} \frac{1}{1 + \sin x}$

Answer:: $lim_{x \to 0} \frac{1}{1 + \sin x} = 1$

8) $lim_{x \to 2} e^{2 x - x^{2}}$

9) $lim_{x \to 1} \frac{2 - 7 x}{x + 6}$

Answer:: $lim_{x \to 1} \frac{2 - 7 x}{x + 6} = - \frac{5}{7}$

10) $lim_{x \to 3} \ln e^{3 x}$

In exercises 11 - 20, use direct substitution to show that each limit leads to the indeterminate form $0 / 0$ . Then, evaluate the limit analytically.

11) $lim_{x \to 4} \frac{x^{2} - 16}{x - 4}$

Answer:: $When x = 4, \frac{x^{2} - 16}{x - 4} = \frac{16 - 16}{4 - 4} = \frac{0}{0};$

then, $lim_{x \to 4} \frac{x^{2} - 16}{x - 4} = lim_{x \to 4} \frac{(x + 4) (x - 4)}{x - 4} = lim_{x \to 4} (x + 4) = 4 + 4 = 8$

12) $lim_{x \to 2} \frac{x - 2}{x^{2} - 2 x}$

13) $lim_{x \to 6} \frac{3 x - 18}{2 x - 12}$

Answer:: $When x = 6, \frac{3 x - 18}{2 x - 12} = \frac{18 - 18}{12 - 12} = \frac{0}{0};$

then, $lim_{x \to 6} \frac{3 x - 18}{2 x - 12} = lim_{x \to 6} \frac{3 (x - 6)}{2 (x - 6)} = lim_{x \to 6} \frac{3}{2} = \frac{3}{2}$

14) $lim_{h \to 0} \frac{{(1 + h)}^{2} - 1}{h}$

15) $lim_{t \to 9} \frac{t - 9}{\sqrt{t} - 3}$

Answer:: $When t = 9, \frac{t - 9}{\sqrt{t} - 3} = \frac{9 - 9}{3 - 3} = \frac{0}{0};$

then, $lim_{t \to 9} \frac{t - 9}{\sqrt{t} - 3} = lim_{t \to 9} \frac{t - 9}{\sqrt{t} - 3} \frac{\sqrt{t} + 3}{\sqrt{t} + 3} = lim_{t \to 9} \frac{(t - 9) (\sqrt{t} + 3)}{t - 9} = lim_{t \to 9} (\sqrt{t} + 3) = \sqrt{9} + 3 = 6$

16) $lim_{h \to 0} \frac{\frac{1}{a + h} - \frac{1}{a}}{h}$ , where $a$ is a real-valued constant

17) $lim_{θ \to π} \frac{\sin θ}{\tan θ}$

Answer:: $When θ = π, \frac{\sin θ}{\tan θ} = \frac{\sin π}{\tan π} = \frac{0}{0};$

then, $lim_{θ \to π} \frac{\sin θ}{\tan θ} = lim_{θ \to π} \frac{\sin θ}{\frac{\sin θ}{\cos θ}} = lim_{θ \to π} \cos θ = \cos π = - 1$

18) $lim_{x \to 1} \frac{x^{3} - 1}{x^{2} - 1}$

19) $lim_{x \to 1 / 2} \frac{2 x^{2} + 3 x - 2}{2 x - 1}$

Answer:: $When x = 1 / 2, \frac{2 x^{2} + 3 x - 2}{2 x - 1} = \frac{\frac{1}{2} + \frac{3}{2} - 2}{1 - 1} = \frac{0}{0};$

then, $lim_{x \to 1 / 2} \frac{2 x^{2} + 3 x - 2}{2 x - 1} = lim_{x \to 1 / 2} \frac{(2 x - 1) (x + 2)}{2 x - 1} = lim_{x \to 1 / 2} (x + 2) = \frac{1}{2} + 2 = \frac{5}{2}$

20) $lim_{x \to - 3} \frac{\sqrt{x + 4} - 1}{x + 3}$

In exercises 21 - 24, use direct substitution to obtain an undefined expression. Then, use the method used in Example 9 of this section to simplify the function and determine the limit.

21) $lim_{x \to - 2^{-}} \frac{2 x^{2} + 7 x - 4}{x^{2} + x - 2}$

Answer:: $- \infty$

22) $lim_{x \to - 2^{+}} \frac{2 x^{2} + 7 x - 4}{x^{2} + x - 2}$

23) $lim_{x \to 1^{-}} \frac{2 x^{2} + 7 x - 4}{x^{2} + x - 2}$

Answer:: $- \infty$

24) $lim_{x \to 1^{+}} \frac{2 x^{2} + 7 x - 4}{x^{2} + x - 2}$

In exercises 25 - 32, assume that $lim_{x \to 6} f (x) = 4, lim_{x \to 6} g (x) = 9$ , and $lim_{x \to 6} h (x) = 6$ . Use these three facts and the limit laws to evaluate each limit.

25) $lim_{x \to 6} 2 f (x) g (x)$

Answer:: $lim_{x \to 6} 2 f (x) g (x) = 2 (lim_{x \to 6} f (x)) (lim_{x \to 6} g (x)) = 2 (4) (9) = 72$

26) $lim_{x \to 6} \frac{g (x) - 1}{f (x)}$

27) $lim_{x \to 6} (f (x) + \frac{1}{3} g (x))$

Answer:: $lim_{x \to 6} (f (x) + \frac{1}{3} g (x)) = lim_{x \to 6} f (x) + \frac{1}{3} lim_{x \to 6} g (x) = 4 + \frac{1}{3} (9) = 7$

28) $lim_{x \to 6} \frac{{(h (x))}^{3}}{2}$

29) $lim_{x \to 6} \sqrt{g (x) - f (x)}$

Answer:: $lim_{x \to 6} \sqrt{g (x) - f (x)} = \sqrt{lim_{x \to 6} g (x) - lim_{x \to 6} f (x)} = \sqrt{9 - 4} = \sqrt{5}$

30) $lim_{x \to 6} x \cdot h (x)$

31) $lim_{x \to 6} [(x + 1) \cdot f (x)]$

Answer:: $lim_{x \to 6} [(x + 1) f (x)] = (lim_{x \to 6} (x + 1)) (lim_{x \to 6} f (x)) = 7 (4) = 28$

32) $lim_{x \to 6} (f (x) \cdot g (x) - h (x))$

[T] In exercises 33 - 35, use a calculator to draw the graph of each piecewise-defined function and study the graph to evaluate the given limits.

33) $f (x) = {\begin{cases} x^{2}, & x \leq 3 \\ x + 4, & x > 3 \end{cases}$

a. $lim_{x \to 3^{-}} f (x)$

b. $lim_{x \to 3^{+}} f (x)$

Answer:

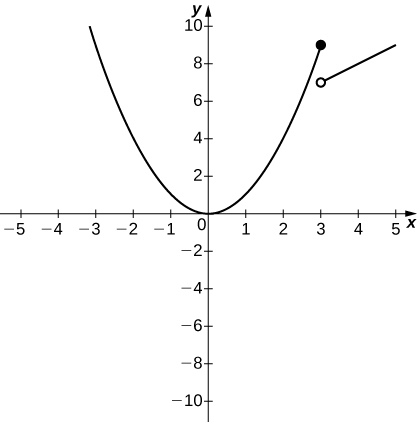
$The graph of a piecewise function with two segments. The first is the parabola x^2, which exists for x<=3. The vertex is at the origin, it opens upward, and there is a closed circle at the endpoint (3,9). The second segment is the line x+4, which is a linear function existing for x > 3. There is an open circle at (3, 7), and the slope is 1.$

a. $9$ ; b. $7$

34) $g (x) = {\begin{cases} x^{3} - 1, & x \leq 0 \\ 1, & x > 0 \end{cases}$

a. $lim_{x \to 0^{-}} g (x)$

b. $lim_{x \to 0^{+}} g (x)$

35) $h (x) = {\begin{cases} x^{2} - 2 x + 1, & x < 2 \\ 3 - x, & x \geq 2 \end{cases}$

a. $lim_{x \to 2^{-}} h (x)$

b. $lim_{x \to 2^{+}} h (x)$

In exercises 36 - 43, use the following graphs and the limit laws to evaluate each limit.

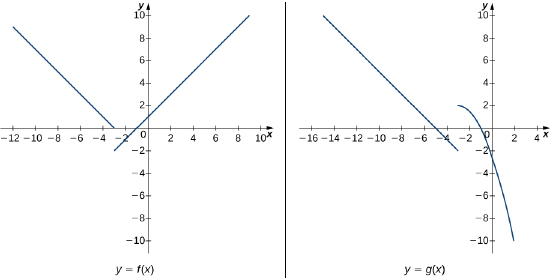
$2.4E5 graphs for 36-43.png$

36) $lim_{x \to - 3^{+}} (f (x) + g (x))$

37) $lim_{x \to - 3^{-}} (f (x) - 3 g (x))$

Answer:: $lim_{x \to - 3^{-}} (f (x) - 3 g (x)) = lim_{x \to - 3^{-}} f (x) - 3 lim_{x \to - 3^{-}} g (x) = 0 + 6 = 6$

38) $lim_{x \to 0} \frac{f (x) g (x)}{3}$

39) $lim_{x \to - 5} \frac{2 + g (x)}{f (x)}$

Answer:: $lim_{x \to - 5} \frac{2 + g (x)}{f (x)} = \frac{2 + (lim_{x \to - 5} g (x))}{lim_{x \to - 5} f (x)} = \frac{2 + 0}{2} = 1$

40) $lim_{x \to 1} {(f (x))}^{2}$

41) $lim_{x \to 1} \sqrt[3]{f (x) - g (x)}$

Answer:: $lim_{x \to 1} \sqrt[3]{f (x) - g (x)} = \sqrt[3]{lim_{x \to 1} f (x) - lim_{x \to 1} g (x)} = \sqrt[3]{2 + 5} = \sqrt[3]{7}$

42) $lim_{x \to - 7} (x \cdot g (x))$

43) $lim_{x \to - 9} [x \cdot f (x) + 2 \cdot g (x)]$

Answer:: $lim_{x \to - 9} (x f (x) + 2 g (x)) = (lim_{x \to - 9} x) (lim_{x \to - 9} f (x)) + 2 lim_{x \to - 9} g (x) = (- 9) (6) + 2 (4) = - 46$

For exercises 44 - 46, evaluate the limit using the squeeze theorem. Use a calculator to graph the functions $f (x)$ , $g (x)$ , and $h (x)$ when possible.

44) [T] True or False? If $2 x - 1 \leq g (x) \leq x^{2} - 2 x + 3$ , then $lim_{x \to 2} g (x) = 0$ .

45) [T] $lim_{θ \to 0} θ^{2} \cos (\frac{1}{θ})$

Answer:

The limit is zero.

$The graph of three functions over the domain [-1,1], colored red, green, and blue as follows: red: theta^2, green: theta^2 * cos (1/theta), and blue: - (theta^2). The red and blue functions open upwards and downwards respectively as parabolas with vertices at the origin. The green function is trapped between the two.$

46) $lim_{x \to 0} f (x)$ , where $f (x) = {\begin{cases} 0, & x rational \\ x^{2}, & x irrrational \end{cases}$

47) [T] In physics, the magnitude of an electric field generated by a point charge at a distance $r$ in vacuum is governed by Coulomb’s law: $E (r) = \frac{q}{4 π ε_{0} r^{2}}$ , where $E$ represents the magnitude of the electric field, $q$ is the charge of the particle, $r$ is the distance between the particle and where the strength of the field is measured, and $\frac{1}{4 π ε_{0}}$ is Coulomb’s constant: $8.988 \times 109 N \cdot m^{2} / C^{2}$ .

a. Use a graphing calculator to graph $E (r)$ given that the charge of the particle is $q = 10^{- 10}$ .

b. Evaluate $lim_{r \to 0^{+}} E (r)$ . What is the physical meaning of this quantity? Is it physically relevant? Why are you evaluating from the right?

Answer:

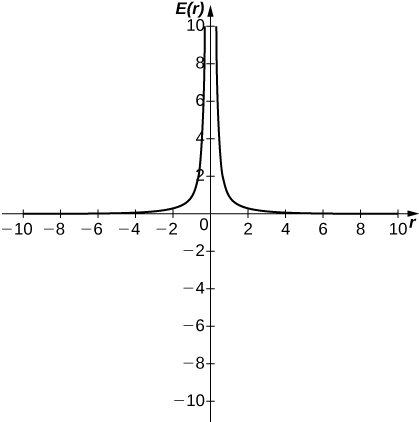
$A graph of a function with two curves. The first is in quadrant two and curves asymptotically to infinity along the y axis and to 0 along the x axis as x goes to negative infinity. The second is in quadrant one and curves asymptotically to infinity along the y axis and to 0 along the x axis as x goes to infinity.$

b. ∞. The magnitude of the electric field as you approach the particle q becomes infinite. It does not make physical sense to evaluate negative distance.

48) [T] The density of an object is given by its mass divided by its volume: $ρ = m / V .$

a. Use a calculator to plot the volume as a function of density $(V = m / ρ)$ , assuming you are examining something of mass $8$ kg ( $m = 8$ ).

b. Evaluate $lim_{x \to 0^{+}} V (ρ)$ and explain the physical meaning.

Contributors and Attributions

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

Search

Text Color

Text Size

Margin Size

Font Type

Contributors and Attributions

Contributors and Attributions

Support Center

How can we help?