2.8E: Exercises for Section 2.7

In exercises 1 - 4, write the appropriate $ε − δ$ definition for each of the given statements.

1) $\displaystyle \lim_{x →a}f(x)=N$

2) $\displaystyle \lim_{t →b}g(t)=M$

Answer

For every $ε >0$, there exists a $δ >0$, so that if $0 <|t −b| < δ$, then $|g(t) −M| < ε$

3) $\displaystyle \lim_{x →c}h(x)=L$

4) $\displaystyle \lim_{x →a} φ(x)=A$

Answer

For every $ε >0$, there exists a $δ >0$, so that if $0 <|x −a| < δ$, then $| φ(x) −A| < ε$

The following graph of the function $f$ satisfies $\displaystyle \lim_{x →2}f(x)=2$. In the following exercises, determine a value of $δ >0$ that satisfies each statement.

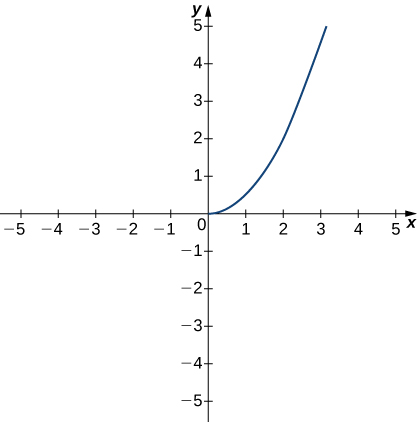
5) If $0 <|x −2| < δ$, then $|f(x) −2| <1$.

6) If $0 <|x −2| < δ$, then $|f(x) −2| <0.5$.

Answer

$δ ≤0.25$

The following graph of the function $f$ satisfies $\displaystyle \lim_{x →3}f(x)= −1$. In the following exercises, determine a value of $δ >0$ that satisfies each statement.

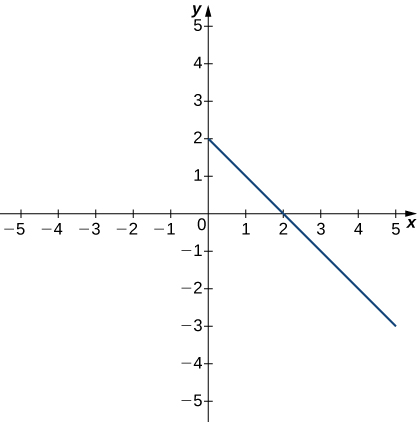
7) If $0 <|x −3| < δ$, then $|f(x)+1| <1$.

8) If $0 <|x −3| < δ$, then $|f(x)+1| <2$.

Answer

$δ ≤2$

The following graph of the function $f$ satisfies $\displaystyle \lim_{x →3}f(x)=2$. In the following exercises, for each value of $ε$, find a value of $δ >0$ such that the precise definition of limit holds true.

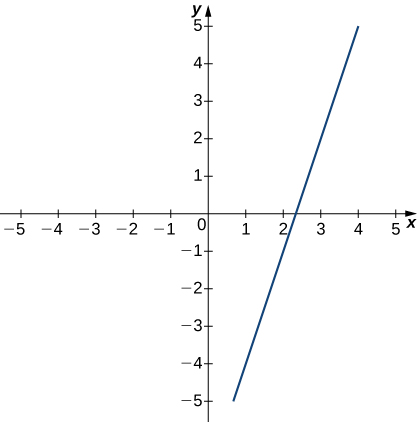
9) $ε=1.5$

10) $ε=3$

Answer

$δ ≤1$

[T] In exercises 11 - 12, use a graphing calculator to find a number $δ$ such that the statements hold true.

11) $\left|\sin(2x) −\frac{1}{2}\right| <0.1$, whenever $\left|x −\frac{ π}{12}\right| < δ$

12) $\left|\sqrt{x −4} −2\right| <0.1$, whenever $|x −8| < δ$

Answer

$δ <0.3900$

In exercises 13 - 17, use the precise definition of limit to prove the given limits.

13) $\displaystyle \lim_{x →2}\,(5x+8)=18$

14) $\displaystyle \lim_{x →3}\frac{x^2 −9}{x −3}=6$

Answer

Let $δ= ε$. If $0 <|x −3| < ε$, then $\left|\dfrac{x^2 −9}{x −3} - 6\right| = \left|\dfrac{(x+3)(x −3)}{x −3} - 6\right| = |x+3 −6|=|x −3| < ε$.

15) $\displaystyle \lim_{x →2}\frac{2x^2 −3x −2}{x −2}=5$

16) $\displaystyle \lim_{x →0}x^4=0$

Answer

Let $δ=\sqrt[4]{ ε}$. If $0 <|x| <\sqrt[4]{ ε}$, then $\left|x^4-0\right|=x^4 < ε$.

17) $\displaystyle \lim_{x →2}\,(x^2+2x)=8$

In exercises 18 - 20, use the precise definition of limit to prove the given one-sided limits.

18) $\displaystyle \lim_{x →5^ −}\sqrt{5 −x}=0$

Answer

Let $δ= ε^2$. If $- ε^2 < x - 5 < 0,$ we can multiply through by $-1$ to get $0 <5-x < ε^2.$
Then $\left|\sqrt{5 −x} - 0\right|=\sqrt{5 −x} < \sqrt{ ε^2} = ε$.

19) $\displaystyle \lim_{x →0^+}f(x)= −2$, where $f(x)=\begin{cases}8x −3, & \text{if }x <0\\4x −2, & \text{if }x ≥0\end{cases}$.

20) $\displaystyle \lim_{x →1^ −}f(x)=3$, where $f(x)=\begin{cases}5x −2, & \text{if }x <1\\7x −1, & \text{if }x ≥1\end{cases}$.

Answer

Let $δ= ε/5$. If $− ε/5 < x - 1 <0,$ we can multiply through by $-1$ to get $0 <1-x < ε/5.$
Then $|f(x) −3|=|5x-2-3| = |5x −5| = 5(1-x),$ since $x <1$ here.
And $5(1-x) < 5( ε/5) = ε$.

In exercises 21 - 23, use the precise definition of limit to prove the given infinite limits.

21) $\displaystyle \lim_{x →0}\frac{1}{x^2}= ∞$

22) $\displaystyle \lim_{x → −1}\frac{3}{(x+1)^2}= ∞$

Answer

Let $δ=\sqrt{\frac{3}{N}}$. If $0 <|x+1| <\sqrt{\frac{3}{N}}$, then $f(x)=\frac{3}{(x+1)^2} >N$.

23) $\displaystyle \lim_{x →2} −\frac{1}{(x −2)^2}= − ∞$

24) An engineer is using a machine to cut a flat square of Aerogel of area $144 \,\text{cm}^2$. If there is a maximum error tolerance in the area of $8 \,\text{cm}^2$, how accurately must the engineer cut on the side, assuming all sides have the same length? How do these numbers relate to $δ$, $ε$, $a$, and $L$?

Answer

$0.033 \text{ cm}, \, ε=8,\, δ=0.33,\,a=12,\,L=144$

25) Use the precise definition of limit to prove that the following limit does not exist: $\displaystyle \lim_{x →1}\frac{|x −1|}{x −1}.$

26) Using precise definitions of limits, prove that $\displaystyle \lim_{x →0}f(x)$ does not exist, given that $f(x)$ is the ceiling function. (Hint: Try any $δ <1$.)

Answer

Answers may very.

27) Using precise definitions of limits, prove that $\displaystyle \lim_{x →0}f(x)$ does not exist: $f(x)=\begin{cases}1, & \text{if }x\text{ is rational}\\0, & \text{if }x\text{ is irrational}\end{cases}$. (Hint: Think about how you can always choose a rational number \(0 <d\), >

28) Using precise definitions of limits, determine $\displaystyle \lim_{x →0}f(x)$ for $f(x)=\begin{cases}x, & \text{if }x\text{ is rational}\\0, & \text{if }x\text{ is irrational}\end{cases}$. (Hint: Break into two cases, $x$ rational and $x$ irrational.)

Answer

$0$

29) Using the function from the previous exercise, use the precise definition of limits to show that $\displaystyle \lim_{x →a}f(x)$ does not exist for $a ≠0$

For exercises 30 - 32, suppose that $\displaystyle \lim_{x →a}f(x)=L$ and $\displaystyle \lim_{x →a}g(x)=M$ both exist. Use the precise definition of limits to prove the following limit laws:

30) $\displaystyle \lim_{x →a}(f(x) −g(x))=L −M$

Answer

$f(x) −g(x)=f(x)+( −1)g(x)$

31) $\displaystyle \lim_{x →a}[cf(x)]=cL$ for any real constant $c$ (Hint: Consider two cases: $c=0$ and $c ≠0$.)

32) $\displaystyle \lim_{x →a}[f(x)g(x)]=LM$. (Hint: $|f(x)g(x) −LM|= |f(x)g(x) −f(x)M +f(x)M −LM| ≤|f(x)||g(x) −M| +|M||f(x) −L|.)$

Answer

Answers may vary.