5.1E: Exercises for Section 5.1
- Last updated
- Mar 16, 2023
- Save as PDF
- Page ID
- 123929
( \newcommand{\kernel}{\mathrm{null}\,}\)
1.) State whether the given sums are equal or unequal.
- 10∑i=1i and 10∑k=1k
- 10∑i=1i and 15∑i=6(i−5)
- 10∑i=1i(i−1) and 9∑j=0(j+1)j
- 10∑i=1i(i−1) and 10∑k=1(k2−k)
- Answer
- a. They are equal; both represent the sum of the first 10 whole numbers.
b. They are equal; both represent the sum of the first 10 whole numbers.
c. They are equal by substituting j=i−1.
d. They are equal; the first sum factors the terms of the second.
In exercises 2 - 3, use the rules for sums of powers of integers to compute the sums.
2) 10∑i=5i
3) 10∑i=5i2
- Answer
- 10∑i=5i2=385−30=355
Suppose that 100∑i=1ai=15 and 100∑i=1bi=−12.
In exercises 4 - 7, compute the sums.
4) 100∑i=1(ai+bi)
5) 100∑i=1(ai−bi)
- Answer
- 100∑i=1(ai−bi)=15−(−12)=27
6) 100∑i=1(3ai−4bi)
7) 100∑i=1(5ai+4bi)
- Answer
- 100∑i=1(5ai+4bi)=5(15)+4(−12)=27
In exercises 8 - 11, use summation properties and formulas to rewrite and evaluate the sums.
8) 20∑k=1100(k2−5k+1)
9) 50∑j=1(j2−2j)
- Answer
- 50∑j=1j2−250∑j=1j=(50)(51)(101)6−2(50)(51)2=40,375
10) 20∑j=11(j2−10j)
11) 25∑k=1[(2k)2−100k]
- Answer
- 425∑k=1k2−10025∑k=1k=4(25)(26)(51)9−50(25)(26)=−10,400
Let Ln denote the left-endpoint sum using n subintervals and let Rn denote the corresponding right-endpoint sum.
In exercises 12 - 19, compute the indicated left and right sums for the given functions on the indicated interval.
12) L4 for f(x)=1x−1 on [2,3]
13) R4 for g(x)=cos(πx) on [0,1]
- Answer
- R4=0.25
14) L6 for f(x)=1x(x−1) on [2,5]
15) R6 for f(x)=1x(x−1) on [2,5]
- Answer
- R6=0.372
16) R4 for 1x2+1 on [−2,2]
17) L4 for 1x2+1 on [−2,2]
- Answer
- L4=2.20
18) R4 for x2−2x+1 on [0,2]
19) L8 for x2−2x+1 on [0,2]
- Answer
- L8=0.6875
20) Compute the left and right Riemann sums— L4 and R4, respectively—for f(x)=(2−|x|) on [−2,2]. Compute their average value and compare it with the area under the graph of f.
21) Compute the left and right Riemann sums— L6 and R6, respectively—for f(x)=(3−|3−x|) on [0,6]. Compute their average value and compare it with the area under the graph of f.
- Answer
- L6=9.000=R6. The graph of f is a triangle with area 9units2.
22) Compute the left and right Riemann sums— L4 and R4, respectively—for f(x)=√4−x2 on [−2,2] and compare their values.
23) Compute the left and right Riemann sums— L6 and R6, respectively—for f(x)=√9−(x−3)2 on [0,6] and compare their values.
- Answer
- L6=13.12899=R6. They are equal.
For exercises 24 - 27, express the following endpoint sums in sigma notation but do not evaluate them.
24) L30 for f(x)=x2 on [1,2]
25) L10 for f(x)=√4−x2 on [−2,2]
- Answer
- L10=41010∑i=1√4−(−2+4(i−1)10)
26) R20 for f(x)=sinx on [0,π]
27) R100 for lnx on [1,e]
- Answer
- R100=e−1100100∑i=1ln(1+(e−1)i100)
In exercises 28 - 33, graph the function then use a calculator or a computer program to evaluate the following left and right endpoint sums. Is the area under the curve between the left and right endpoint sums?
28) [T] L100 and R100 for y=x2−3x+1 on the interval [−1,1]
29) [T] L100 and R100 for y=x2 on the interval [0,1]
- Answer
-
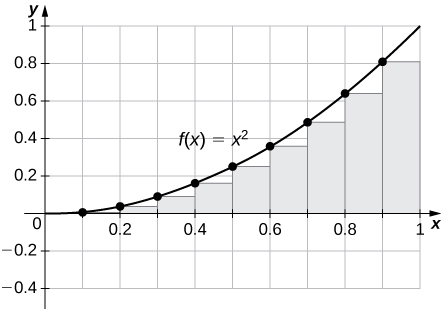
R100=0.33835,L100=0.32835.
The plot shows that the left Riemann sum is an underestimate because the function is increasing. Similarly, the right Riemann sum is an overestimate. The area lies between the left and right Riemann sums. Ten rectangles are shown for visual clarity. This behavior persists for more rectangles.
30) [T] L50 and R50 for y=x+1x2−1 on the interval [2,4]
31) [T] L100 and R100 for y=x3 on the interval [−1,1]
- Answer
-
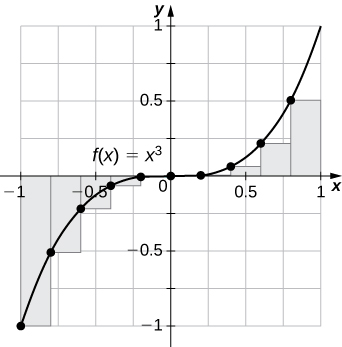
L100=−0.02,R100=0.02.
The left endpoint sum is an underestimate because the function is increasing. Similarly, a right endpoint approximation is an overestimate. The area lies between the left and right endpoint estimates.
32) [T] L50 and R50 for y=tan(x) on the interval [0,π4]
33) [T] L100 and R100 for y=e2x on the interval [−1,1]
- Answer
-
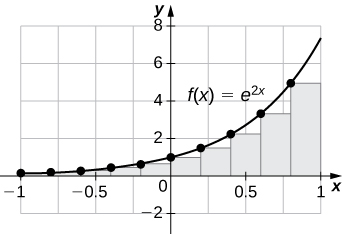
L100=3.555,R100=3.670.
The plot shows that the left Riemann sum is an underestimate because the function is increasing. Ten rectangles are shown for visual clarity. This behavior persists for more rectangles.
34) Let tj denote the time that it took Tejay van Garteren to ride the jth stage of the Tour de France in 2014. If there were a total of 21 stages, interpret 21∑j=1tj.
35) Let rj denote the total rainfall in Portland on the jth day of the year in 2009. Interpret 31∑j=1rj.
- Answer
- The sum represents the cumulative rainfall in January 2009.
36) Let dj denote the hours of daylight and δj denote the increase in the hours of daylight from day j−1 to day j in Fargo, North Dakota, on the jth day of the year. Interpret d1+365∑j=2δj.
37) To help get in shape, Joe gets a new pair of running shoes. If Joe runs 1 mi each day in week 1 and adds 110 mi to his daily routine each week, what is the total mileage on Joe’s shoes after 25 weeks?
- Answer
- The total mileage is 7×25∑i=1(1+(i−1)10)=7×25+710×12×25=385 mi.
38) The following table gives approximate values of the average annual atmospheric rate of increase in carbon dioxide (CO2) each decade since 1960, in parts per million (ppm). Estimate the total increase in atmospheric CO2 between 1964 and 2013.
| Decade | Ppm/y |
|---|---|
| 1964-1973 | 1.07 |
| 1976-1983 | 1.34 |
| 1984-1993 | 1.40 |
| 1994-2003 | 1.87 |
| 2004-2013 | 2.07 |
Average Annual Atmospheric CO2 Increase, 1964–2013 Source: http://www.esrl.noaa.gov/gmd/ccgg/trends/.
39) The following table gives the approximate increase in sea level in inches over 20 years starting in the given year. Estimate the net change in mean sea level from 1870 to 2010.
| Starting Year | 20- Year Change |
|---|---|
| 1870 | 0.3 |
| 1890 | 1.5 |
| 1910 | 0.2 |
| 1930 | 2.8 |
| 1950 | 0.7 |
| 1970 | 1.1 |
| 1990 | 1.5 |
Approximate 20-Year Sea Level Increases, 1870–1990
Source: http://link.springer.com/article/10....712-011-9119-1
- Answer
- Add the numbers to get 8.1-in. net increase.
40) The following table gives the approximate increase in dollars in the average price of a gallon of gas per decade since 1950. If the average price of a gallon of gas in 2010 was $2.60, what was the average price of a gallon of gas in 1950?
| Starting Year | 10- Year Change |
|---|---|
| 1950 | 0.03 |
| 1960 | 0.05 |
| 1970 | 0.86 |
| 1980 | −0.03 |
| 1990 | 0.29 |
| 2000 | 1.12 |
Approximate 10-Year Gas Price Increases, 1950–2000
Source: epb.lbl.gov/homepages/Rick_Di...011-trends.pdf.
41) The following table gives the percent growth of the U.S. population beginning in July of the year indicated. If the U.S. population was 281,421,906 in July 2000, estimate the U.S. population in July 2010.
| Year | % Change/Year |
|---|---|
| 2000 | 1.12 |
| 2001 | 0.99 |
| 2002 | 0.93 |
| 2003 | 0.86 |
| 2004 | 0.93 |
| 2005 | 0.93 |
| 2006 | 0.97 |
| 2007 | 0.96 |
| 2008 | 0.95 |
| 2009 | 0.88 |
Annual Percentage Growth of U.S. Population, 2000–2009
Source: www.census.gov/popest/data.
(Hint: To obtain the population in July 2001, multiply the population in July 2000 by 1.0112 to get 284,573,831.)
- Answer
- 309,389,957
In exercises 42 - 45, estimate the areas under the curves by computing the left Riemann sums, L8.
42)
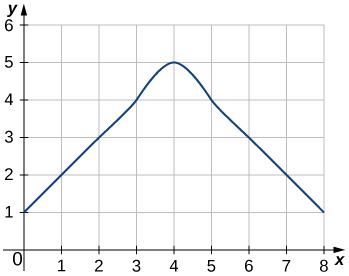
43)
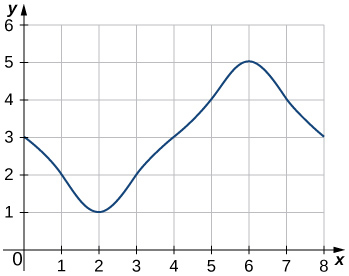
- Answer
- L8=3+2+1+2+3+4+5+4=24
44)
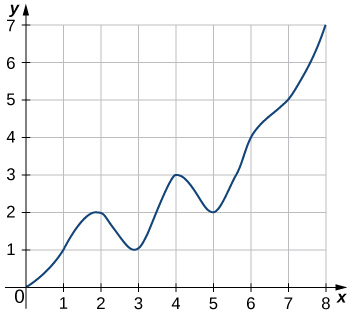
45)
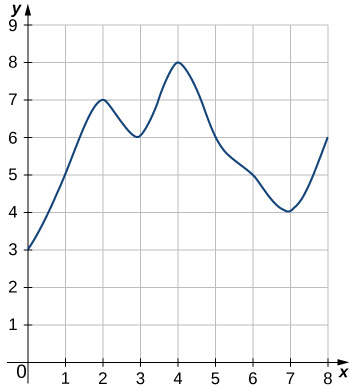
- Answer
- L8=3+5+7+6+8+6+5+4=44
46) [T] Use a computer algebra system to compute the Riemann sum, LN, for N=10,30,50 for f(x)=√1−x2 on [−1,1].
47) [T] Use a computer algebra system to compute the Riemann sum, LN, for N=10,30,50 for f(x)=1√1+x2 on [−1,1].
- Answer
- L10≈1.7604,L30≈1.7625,L50≈1.76265
48) [T] Use a computer algebra system to compute the Riemann sum, LN, for N=10,30,50 for f(x)=sin2x on [0,2π]. Compare these estimates with π.
In exercises 49-50, use a calculator or a computer program to evaluate the endpoint sums RN and LN for N=1,10,100. How do these estimates compare with the exact answers, which you can find via geometry?
49) [T] y=cos(πx) on the interval [0,1]
- Answer
- R1=−1,L1=1,
R10=−0.1,L10=0.1,
L100=0.01,R100=−0.01.
By symmetry of the graph, the exact area is zero.
50) [T] y=3x+2 on the interval [3,5]
In exercises 51 - 52, use a calculator or a computer program to evaluate the endpoint sums RN and LN for N=1,10,100.
51) [T] y=x4−5x2+4 on the interval [−2,2], which has an exact area of 3215
- Answer
- R1=0,L1=0,
R10=2.4499,L10=2.4499,
R100=2.1365,L100=2.1365
52) [T] y=lnx on the interval [1,2], which has an exact area of 2ln(2)−1
53) Explain why, if f(a)≥0 and f is increasing on [a,b], that the left endpoint estimate is a lower bound for the area below the graph of f on [a,b].
- Answer
- If [c,d]is a subinterval of [a,b] under one of the left-endpoint sum rectangles, then the area of the rectangle contributing to the left-endpoint estimate is f(c)(d−c). But, f(c)≤f(x) for c≤x≤d, so the area under the graph of f between c and d is f(c)(d−c) plus the area below the graph of f but above the horizontal line segment at height f(c), which is positive. As this is true for each left-endpoint sum interval, it follows that the left Riemann sum is less than or equal to the area below the graph of f on [a,b].
54) Explain why, if f(b)≥0 and f is decreasing on [a,b], that the left endpoint estimate is an upper bound for the area below the graph of f on [a,b].
55) Show that, in general, RN−LN=(b−a)×f(b)−f(a)N.
- Answer
- LN=b−aNN∑i=1f(a+(b−a)i−1N)=b−aNN−1∑i=0f(a+(b−a)iN) and RN=b−aNN∑i=1f(a+(b−a)iN). The left sum has a term corresponding to i=0 and the right sum has a term corresponding to i=N. In RN−LN, any term corresponding to i=1,2,…,N−1 occurs once with a plus sign and once with a minus sign, so each such term cancels and one is left with RN−LN=b−aN(f(a+(b−a))NN)−(f(a)+(b−a)0N)=b−aN(f(b)−f(a)).
56) Explain why, if f is increasing on [a,b], the error between either LN or RN and the area A below the graph of f is at most (b−a)f(b)−f(a)N.
57) For each of the three graphs:
a. Obtain a lower bound L(A) for the area enclosed by the curve by adding the areas of the squares enclosed completely by the curve.
b. Obtain an upper bound U(A) for the area by adding to L(A) the areas B(A) of the squares enclosed partially by the curve.
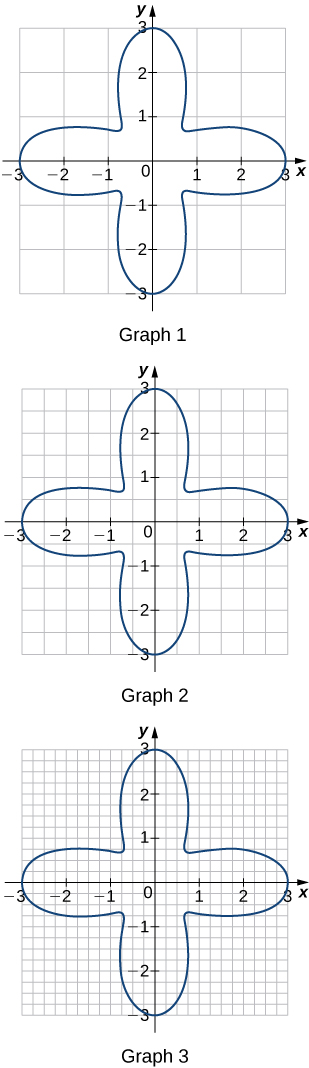
- Answer
- Graph 1: a. L(A)=0,B(A)=20;b.U(A)=20.
Graph 2: a.L(A)=9;b.B(A)=11,U(A)=20.
Graph 3: a. L(A)=11.0;b.B(A)=4.5,U(A)=15.5.
58) In the previous exercise, explain why L(A) gets no smaller while U(A) gets no larger as the squares are subdivided into four boxes of equal area.
59) A unit circle is made up of n wedges equivalent to the inner wedge in the figure. The base of the inner triangle is 1 unit and its height is sin(πn). The base of the outer triangle is B=cos(πn)+sin(πn)tan(πn) and the height is H=Bsin(2πn). Use this information to argue that the area of a unit circle is equal to π.
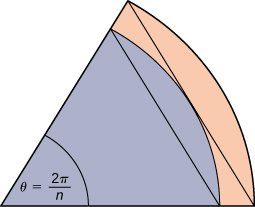
- Answer
- Let A be the area of the unit circle. The circle encloses n congruent triangles each of area sin(2πn)2, so n2sin(2πn)≤A. Similarly, the circle is contained inside n congruent triangles each of area BH2=12(cos(πn)+sin(πn)tan(πn))sin(2πn), so A≤n2sin(2πn)(cos(πn))+sin(πn)tan(πn). As n→∞,n2sin(2πn)=πsin(2πn)(2πn)→π, so we conclude π≤A. Also, as n→∞,cos(πn)+sin(πn)tan(πn)→1, so we also have A≤π. By the squeeze theorem for limits, we conclude that A=π.

