2.4: Infinite Limits

Learning Objectives

• Using correct notation, describe an infinite limit.
• Define a vertical asymptote.

Let's continue our exploration of limits by considering the graph of the function

$h(x)=\dfrac{1}{(x−2)^2}$,

shown in Figure $\PageIndex{1}$. In particular, let’s focus our attention on the behavior of this graph at and around $x=2$.

Figure $\PageIndex{1}$: Consider the behavior of this function around $x=2$.

 

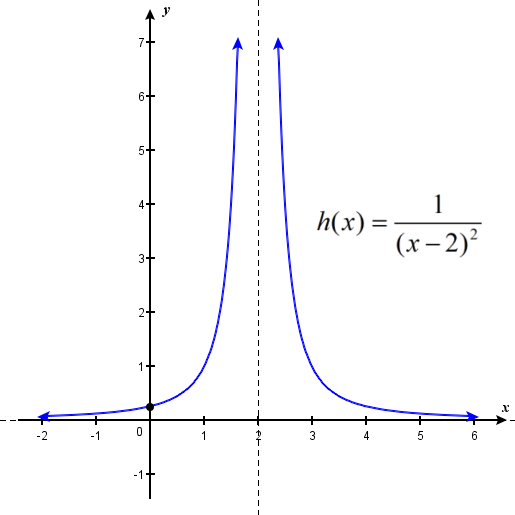
Infinite Limits

Evaluating the limit of a function at a point or evaluating the limit of a function from the right and left at a point helps us to characterize the behavior of a function around a given value. As we shall see, we can also describe the behavior of functions that do not have finite limits.

We now turn our attention to $h(x)=1/(x−2)^2$, the third and final function introduced at the beginning of this section (see Figure $\PageIndex{1}$). From its graph we see that as the values of $x$ approach $2$, the values of $h(x)=1/(x−2)^2$ become larger and larger and, in fact, become infinite. Mathematically, we say that the limit of $h(x)$ as $x$ approaches $2$ is positive infinity. Symbolically, we express this idea as

$$\lim_{x \to 2}h(x)=+∞. \nonumber$$

More generally, we define infinite limits as follows:

Definitions: Infinite Limits

We define three types of infinite limits.

Infinite limits from the left: Let $f(x)$ be a function defined at all values in an open interval of the form $(b,a)$.

i. If the values of $f(x)$ increase without bound as the values of $x$ (where $x<a$) approach the number $a$, then we say that the limit as $x$ approaches $a$ from the left is positive infinity and we write $$\lim_{x \to a^−}f(x)=+∞.$$

ii. If the values of $f(x)$ decrease without bound as the values of $x$ (where $x<a$) approach the number $a$, then we say that the limit as $x$ approaches $a$ from the left is negative infinity and we write $$\lim_{x \to a^−}f(x)=−∞.$$

Infinite limits from the right: Let $f(x)$ be a function defined at all values in an open interval of the form $(a,c)$.

i. If the values of $f(x)$ increase without bound as the values of $x$ (where $x>a$) approach the number $a$, then we say that the limit as $x$ approaches $a$ from the left is positive infinity and we write $$\lim_{x \to a^+}f(x)=+∞.$$

ii. If the values of $f(x)$ decrease without bound as the values of $x$ (where $x>a$) approach the number $a$, then we say that the limit as $x$ approaches $a$ from the left is negative infinity and we write $$\lim_{x \to a^+}f(x)=−∞.$$

Two-sided infinite limit: Let $f(x)$ be defined for all $x≠a$ in an open interval containing $a$

i. If the values of $f(x)$ increase without bound as the values of $x$ (where $x≠a$) approach the number $a$, then we say that the limit as $x$ approaches $a$ is positive infinity and we write $$\lim_{x \to a} f(x)=+∞.$$

ii. If the values of $f(x)$ decrease without bound as the values of $x$ (where $x≠a$) approach the number $a$, then we say that the limit as $x$ approaches $a$ is negative infinity and we write $$\lim_{x \to a}f(x)=−∞.$$

It is important to understand that when we write statements such as $\displaystyle \lim_{x \to a}f(x)=+∞$ or $\displaystyle \lim_{x \to a}f(x)=−∞$ we are describing the behavior of the function, as we have just defined it. We are not asserting that a limit exists. For the limit of a function $f(x)$ to exist at $a$, it must approach a real number $L$ as $x$ approaches $a$. That said, if, for example, $\displaystyle \lim_{x \to a}f(x)=+∞$, we always write $\displaystyle \lim_{x \to a}f(x)=+∞$ rather than $\displaystyle \lim_{x \to a}f(x)$ DNE.

Example $\PageIndex{1}$: Recognizing an Infinite Limit

Evaluate each of the following limits, if possible. Use a table of functional values and graph $f(x)=1/x$ to confirm your conclusion.

1. $\displaystyle \lim_{x \to 0^−} \frac{1}{x}$
2. $\displaystyle \lim_{x \to 0^+} \frac{1}{x}$
3. $\displaystyle \lim_{x \to 0}\frac{1}{x}$

Solution

Begin by constructing a table of functional values.

Table $\PageIndex{1}$

$x$	$\dfrac{1}{x}$	$x$	$\dfrac{1}{x}$
-0.1	-10	0.1	10
-0.01	-100	0.01	100
-0.001	-1000	0.001	1000
-0.0001	-10,000	0.0001	10,000
-0.00001	-100,000	0.00001	100,000
-0.000001	-1,000,000	0.000001	1,000,000

a. The values of $1/x$ decrease without bound as $x$ approaches $0$ from the left. We conclude that

$$\lim_{x \to 0^−}\frac{1}{x}=−∞.\nonumber$$

b. The values of $1/x$ increase without bound as $x$ approaches $0$ from the right. We conclude that

$$\lim_{x \to 0^+}\frac{1}{x}=+∞. \nonumber$$

c. Since $\displaystyle \lim_{x \to 0^−}\frac{1}{x}=−∞$ and $\displaystyle \lim_{x \to 0^+}\frac{1}{x}=+∞$ have different values, we conclude that

$$\lim_{x \to 0}\frac{1}{x}\quad\text{DNE.} \nonumber$$

The graph of $f(x)=1/x$ in Figure $\PageIndex{2}$ confirms these conclusions.

Figure $\PageIndex{2}$: The graph of $f(x)=1/x$ confirms that the limit as $x$ approaches $0$ does not exist.

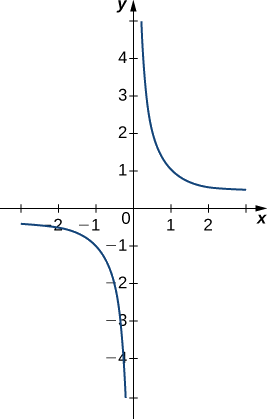
Exercise $\PageIndex{1}$

Evaluate each of the following limits, if possible. Use a table of functional values and graph $f(x)=1/x^2$ to confirm your conclusion.

1. $\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}$
2. $\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}$
3. $\displaystyle \lim_{x \to 0}\frac{1}{x^2}$

Hint

Follow the procedures from Example $\PageIndex{1}$.

Answer

a. $\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}=+∞$;

b. $\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}=+∞$;

c. $\displaystyle \lim_{x \to 0}\frac{1}{x^2}=+∞$

It is useful to point out that functions of the form $f(x)=1/(x−a)^n$, where n is a positive integer, have infinite limits as $x$ approaches $a$ from either the left or right (Figure $\PageIndex{3}$). These limits are summarized in the above definitions.

Figure $\PageIndex{3}$: The function $f(x)=1/(x−a)^n$ has infinite limits at $a$.

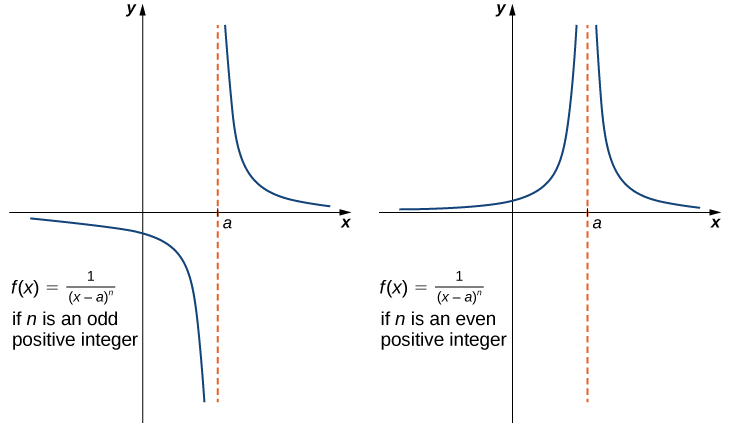
Infinite Limits from Positive Integer Exponents on Denominator of a Rational Function

If $n$ is a positive even integer, then

$$\lim_{x \to a}\frac{1}{(x−a)^n}=+∞.\label{infLim1}$$

If $n$ is a positive odd integer, then

$$\lim_{x \to a^+}\frac{1}{(x−a)^n}=+∞\label{infLim2}$$

and

$$\lim_{x \to a^−}\frac{1}{(x−a)^n}=−∞.\label{infLim3}$$

We should also point out that in the graphs of $f(x)=1/(x−a)^n$, points on the graph having $x$-coordinates very near to a are very close to the vertical line $x=a$. That is, as $x$ approaches $a$, the points on the graph of $f(x)$ are closer to the line $x=a$. The line $x=a$ is called a vertical asymptote of the graph. We formally define a vertical asymptote as follows:

Definition: Vertical Asymptotes

Let $f(x)$ be a function. If any of the following conditions hold, then the line $x=a$ is a vertical asymptote of $f(x)$.

$$\lim_{x \to a^−}f(x)=+∞$$

$$\lim_{x \to a^−}f(x)=−∞$$

$$\lim_{x \to a^+}f(x)=+∞$$

$$\lim_{x \to a^+}f(x)=−∞$$

$$\lim_{x \to a}f(x)=+∞$$

$$\lim_{x \to a}f(x)=−∞$$

Example $\PageIndex{2}$: Finding a Vertical Asymptote

Evaluate each of the following limits using Equations $\ref{infLim1}$, $\ref{infLim2}$, and $\ref{infLim3}$ above. Identify any vertical asymptotes of the function $f(x)=1/(x+3)^4.$

1. $\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}$
2. $\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}$
3. $\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}$

Solution

We can use the above equations directly.

1. $\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}=+∞$
2. $\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}=+∞$
3. $\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}=+∞$

The function $f(x)=1/(x+3)^4$ has a vertical asymptote of $x=−3$.

Exercise $\PageIndex{2}$

Evaluate each of the following limits. Identify any vertical asymptotes of the function $f(x)=\dfrac{1}{(x−2)^3}$.

1. $\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}$
2. $\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}$
3. $\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}$

Answer a

$\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}=−∞$

Answer b

$\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}=+∞$

Answer c

$\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}$   DNE. The line $x=2$ is the vertical asymptote of $f(x)=1/(x−2)^3.$

In the next example we put our knowledge of various types of limits to use to analyze the behavior of a function at several different points.

Example $\PageIndex{3}$: Behavior of a Function at Different Points

Use the graph of $f(x)$ in Figure $\PageIndex{4}$ to determine each of the following values:

1. $\displaystyle \lim_{x \to −4^−}f(x)$;   $\displaystyle \lim_{x \to −4^+}f(x)$;    $\displaystyle \lim_{x→−4}f(x);\;f(−4)$
2. $\displaystyle \lim_{x \to −2^−}f(x$);   $\displaystyle \lim_{x \to −2^+}f(x)$;    $\displaystyle \lim_{x→−2}f(x);\;f(−2)$
3. $\displaystyle \lim_{x \to 1^−}f(x)$;   $\displaystyle \lim_{x \to 1^+}f(x)$;    $\displaystyle \lim_{x \to 1}f(x);\;f(1)$
4. $\displaystyle \lim_{x \to 3^−}f(x)$;   $\displaystyle \lim_{x \to 3^+}f(x)$;    $\displaystyle \lim_{x \to 3}f(x);\;f(3)$

Figure $\PageIndex{4}$: The graph shows $f(x)$.

Solution

Using the definitions above and the graph for reference, we arrive at the following values:

1. $\displaystyle \lim_{x \to −4^−}f(x)=0$;   $\displaystyle \lim_{x \to −4^+}f(x)=0$;    $\displaystyle \lim_{x \to −4}f(x)=0;\;f(−4)=0$
2. $\displaystyle \lim_{x \to −2^−}f(x)=3$;    $\displaystyle \lim_{x \to −2^+}f(x)=3$;    $\displaystyle \lim_{x \to −2}f(x)=3;\;f(−2)$ is undefined
3. $\displaystyle \lim_{x \to 1^−}f(x)=6$;    $\displaystyle \lim_{x \to 1^+}f(x)=3$;   $\displaystyle \lim_{x \to 1}f(x)$  DNE;    $f(1)=6$
4. $\displaystyle \lim_{x \to 3^−}f(x)=−∞$;    $\displaystyle \lim_{x \to 3^+}f(x)=−∞$;    $\displaystyle \lim_{x \to 3}f(x)=−∞$;   $f(3)$ is undefined

Example $\PageIndex{4}$: Einstein’s Equation

In the Chapter opener we mentioned briefly how Albert Einstein showed that a limit exists to how fast any object can travel. Given Einstein’s equation for the mass of a moving object

$$m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber$$

what is the value of this bound?

Figure $\PageIndex{5}$. (Crefit:NASA)

Solution

Our starting point is Einstein’s equation for the mass of a moving object,

$$m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber$$

where $m_0$ is the object’s mass at rest, $v$ is its speed, and $c$ is the speed of light. To see how the mass changes at high speeds, we can graph the ratio of masses $m/m_0$ as a function of the ratio of speeds, $v/c$ (Figure $\PageIndex{6}$).

Figure $\PageIndex{6}$: This graph shows the ratio of masses as a function of the ratio of speeds in Einstein’s equation for the mass of a moving object.

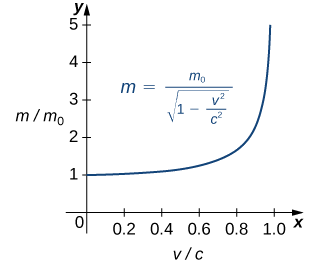
We can see that as the ratio of speeds approaches 1—that is, as the speed of the object approaches the speed of light—the ratio of masses increases without bound. In other words, the function has a vertical asymptote at $v/c=1$. We can try a few values of this ratio to test this idea.

Table $\PageIndex{2}$

$v/c$	$\sqrt{1-\frac{v^2}{c^2}}$	$m/m_o$
0.99	0.1411	7.089
0.999	0.0447	22.37
0.9999	0.0141	70.7

Thus, according to Table $\PageIndex{2}$:, if an object with mass 100 kg is traveling at 0.9999c, its mass becomes 7071 kg. Since no object can have an infinite mass, we conclude that no object can travel at or more than the speed of light.

 

Key Concepts

• A table of values or graph may be used to estimate a limit.
• We may use limits to describe infinite behavior of a function at a point.

Key Equations

• Infinite Limits from the Left

$\displaystyle \lim_{x \to a^−}f(x)=+∞ \qquad \lim_{x \to a^−} f(x)=−∞$

• Infinite Limits from the Right

$\displaystyle \lim_{x \to a^+}f(x)=+∞ \qquad \lim_{x \to a^+} f(x)=−∞$

• Two-Sided Infinite Limits

$\displaystyle \lim_{x \to a}f(x)=+∞$: $\displaystyle \lim_{x \to a^−}f(x)=+∞$ and $\displaystyle \lim_{x \to a^+} f(x)=+∞$

$\displaystyle \lim_{x \to a}f(x)=−∞$: $\displaystyle \lim_{x \to a^−}f(x)=−∞$ and $\displaystyle \lim_{x \to a^+} f(x)=−∞$

 

Glossary

infinite limit

A function has an infinite limit at a point $a$ if it either increases or decreases without bound as it approaches $a$

vertical asymptote

A function has a vertical asymptote at $x=a$ if the limit as $x$ approaches $a$ from the right or left is infinite

Contributors and Attributions

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.