14.7: Variation of Parameters
- Page ID
- 128082
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we give a method called variation of parameters for finding a particular solution of
\[\label{eq:5.7.1} P_0(x)y''+P_1(x)y'+P_2(x)y=F(x)\]
if we know a fundamental set \(\{y_1,y_2\}\) of solutions of the complementary equation
\[\label{eq:5.7.2} P_0(x)y''+P_1(x)y'+P_2(x)y=0.\]
Having found a particular solution \(y_p\) by this method, we can write the general solution of Equation \ref{eq:5.7.1} as
\[y=y_p+c_1y_1+c_2y_2. \nonumber \]
Since we need only one nontrivial solution of Equation \ref{eq:5.7.2} to find the general solution of Equation \ref{eq:5.7.1} by reduction of order, it is natural to ask why we are interested in variation of parameters, which requires two linearly independent solutions of Equation \ref{eq:5.7.2} to achieve the same goal. Here’s the answer:
- If we already know two linearly independent solutions of Equation \ref{eq:5.7.2} then variation of parameters will probably be simpler than reduction of order.
- Variation of parameters generalizes naturally to a method for finding particular solutions of higher order linear equations (Section 9.4) and linear systems of equations (Section 10.7), while reduction of order doesn’t.
- Variation of parameters is a powerful theoretical tool used by researchers in differential equations. Although a detailed discussion of this is beyond the scope of this book, you can get an idea of what it means from Exercises 5.7.37–5.7.39.
We’ll now derive the method. As usual, we consider solutions of Equation \ref{eq:5.7.1} and Equation \ref{eq:5.7.2} on an interval \((a,b)\) where \(P_0\), \(P_1\), \(P_2\), and \(F\) are continuous and \(P_0\) has no zeros. Suppose that \(\{y_1,y_2\}\) is a fundamental set of solutions of the complementary equation Equation \ref{eq:5.7.2}. We look for a particular solution of Equation \ref{eq:5.7.1} in the form
\[\label{eq:5.7.3} y_p=u_1y_1+u_2y_2\]
where \(u_1\) and \(u_2\) are functions to be determined so that \(y_p\) satisfies Equation \ref{eq:5.7.1}. You may not think this is a good idea, since there are now two unknown functions to be determined, rather than one. However, since \(u_1\) and \(u_2\) have to satisfy only one condition (that \(y_p\) is a solution of Equation \ref{eq:5.7.1}), we can impose a second condition that produces a convenient simplification, as follows.
Differentiating Equation \ref{eq:5.7.3} yields
\[\label{eq:5.7.4} y_p'=u_1y_1'+u_2y_2'+u_1'y_1+u_2'y_2.\]
As our second condition on \(u_1\) and \(u_2\) we require that
\[\label{eq:5.7.5} u_1'y_1+u_2'y_2=0.\]
Then Equation \ref{eq:5.7.4} becomes
\[y_p'=u_1y_1'+u_2y_2'; \label{eq:5.7.6}\]
that is, Equation \ref{eq:5.7.5} permits us to differentiate \(y_p\) (once!) as if \(u_1\) and \(u_2\) are constants. Differentiating Equation \ref{eq:5.7.4} yields
\[\label{eq:5.7.7} y_p''=u_1y''_1+u_2y''_2+u_1'y_1'+u_2'y_2'.\]
(There are no terms involving \(u_1''\) and \(u_2''\) here, as there would be if we hadn’t required Equation \ref{eq:5.7.5}.) Substituting Equation \ref{eq:5.7.3}, Equation \ref{eq:5.7.6}, and Equation \ref{eq:5.7.7} into Equation \ref{eq:5.7.1} and collecting the coefficients of \(u_1\) and \(u_2\) yields
\[u_1(P_0y''_1+P_1y_1'+P_2y_1)+u_2(P_0y''_2+P_1y_2'+P_2y_2) +P_0(u_1'y_1'+u_2'y_2')=F. \nonumber \]
As in the derivation of the method of reduction of order, the coefficients of \(u_1\) and \(u_2\) here are both zero because \(y_1\) and \(y_2\) satisfy the complementary equation. Hence, we can rewrite the last equation as
\[\label{eq:5.7.8} P_0(u_1'y_1'+u_2'y_2')=F.\]
Therefore \(y_p\) in Equation \ref{eq:5.7.3} satisfies Equation \ref{eq:5.7.1} if
\[\label{eq:5.7.9} \begin{array}{rcl} u_1'y_1+u_2'y_2 &= 0 \\ u_1'y_1'+u_2'y_2' &= {F\over P_0}, \end{array}\]
where the first equation is the same as Equation \ref{eq:5.7.5} and the second is from Equation \ref{eq:5.7.8}.
We’ll now show that you can always solve Equation \ref{eq:5.7.9} for \(u_1'\) and \(u_2'\). (The method that we use here will always work, but simpler methods usually work when you’re dealing with specific equations.) To obtain \(u_1'\), multiply the first equation in Equation \ref{eq:5.7.9} by \(y_2'\) and the second equation by \(y_2\). This yields
\[\begin{aligned} u_1'y_1y_2'+u_2'y_2y_2'&= 0 \\ u_1'y_1'y_2+u_2'y_2'y_2 &= {Fy_2\over P_0}.\end{aligned}\]
Subtracting the second equation from the first yields
\[\label{eq:5.7.10} u_1'(y_1y_2'-y_1'y_2)=-{Fy_2\over P_0}.\]
Since \(\{y_1,y_2\}\) is a fundamental set of solutions of Equation \ref{eq:5.7.2} on \((a,b)\), Theorem 5.1.6 implies that the Wronskian \(y_1y_2'-y_1'y_2\) has no zeros on \((a,b)\). Therefore we can solve Equation \ref{eq:5.7.10} for \(u_1'\), to obtain
\[\label{eq:5.7.11} u_1'=-{Fy_2\over P_0(y_1y_2'-y_1'y_2)}.\]
We leave it to you to start from Equation \ref{eq:5.7.9} and show by a similar argument that
\[\label{eq:5.7.12} u_2'={Fy_1\over P_0(y_1y_2'-y_1'y_2)}.\]
We can now obtain \(u_1\) and \(u_2\) by integrating \(u_1'\) and \(u_2'\). The constants of integration can be taken to be zero, since any choice of \(u_1\) and \(u_2\) in Equation \ref{eq:5.7.3} will suffice.
You should not memorize Equation \ref{eq:5.7.11} and Equation \ref{eq:5.7.12}. On the other hand, you don’t want to rederive the whole procedure for every specific problem. We recommend the a compromise:
- Write \[\label{eq:5.7.13} y_p=u_1y_1+u_2y_2\] to remind yourself of what you’re doing.
- Write the system \[\label{eq:5.7.14} \begin{array}{rcl} u_1'y_1+u_2'y_2 &= 0 \\ u_1'y_1'+u_2'y_2' &= {F\over P_0} \end{array}\] for the specific problem you’re trying to solve.
- Solve Equation \ref{eq:5.7.14} for \(u_1'\) and \(u_2'\) by any convenient method.
- Obtain \(u_1\) and \(u_2\) by integrating \(u_1'\) and \(u_2'\), taking the constants of integration to be zero.
- Substitute \(u_1\) and \(u_2\) into Equation \ref{eq:5.7.13} to obtain \(y_p\).
Below is a video on using variation of parameters to solve a differential equation.
Below is another video on using variation of parameters to solve a differential equation.
Find a particular solution \(y_p\) of
\[\label{eq:5.7.15} x^2y''-2xy'+2y=x^{9/2},\]
given that \(y_1=x\) and \(y_2=x^2\) are solutions of the complementary equation
\[x^2y''-2xy'+2y=0. \nonumber \]
Then find the general solution of Equation \ref{eq:5.7.15}.
Solution
We set
\[y_p=u_1x+u_2x^2, \nonumber \]
where
\[\begin{aligned} u_1'x+\phantom{2}u_2'x^2&=0\\ u_1'\phantom{x}+2u_2'x\phantom{^2}&={x^{9/2}\over x^2}=x^{5/2}.\end{aligned}\]
From the first equation, \(u_1'=-u_2'x\). Substituting this into the second equation yields \(u_2'x=x^{5/2}\), so \(u_2'=x^{3/2}\) and therefore \(u_1'=-u_2'x=-x^{5/2}\). Integrating and taking the constants of integration to be zero yields
\[u_1=-{2\over7}x^{7/2}\quad \text{and} \quad u_2={2\over5}x^{5/2}. \nonumber \]
Therefore
\[y_p=u_1x+u_2x^2 =-{2\over7}x^{7/2}x+{2\over5}x^{5/2}x^2={4\over35}x^{9/2}, \nonumber \]
and the general solution of Equation \ref{eq:5.7.15} is
\[y={4\over35}x^{9/2}+c_1x+c_2x^2. \nonumber \]
Below is a video on using variation of parameters to solve a differential equation.
Find a particular solution \(y_p\) of
\[\label{eq:5.7.16} (x-1)y''-xy'+y=(x-1)^2,\]
given that \(y_1=x\) and \(y_2=e^x\) are solutions of the complementary equation
\[(x-1)y''-xy'+y=0. \nonumber \]
Then find the general solution of Equation \ref{eq:5.7.16}.
Solution
We set
\[y_p=u_1x+u_2e^x, \nonumber \]
where
\[\begin{aligned} u_1'x+u_2'e^x&=0\\ u_1'\phantom{x}+u_2'e^x&={(x-1)^2\over x-1}=x-1.\end{aligned}\]
Subtracting the first equation from the second yields \(-u_1'(x-1)=x-1\), so \(u_1'=-1\). From this and the first equation, \(u_2'=-xe^{-x}u_1'=xe^{-x}\). Integrating and taking the constants of integration to be zero yields
\[u_1=-x \quad \text{and} \quad u_2=-(x+1)e^{-x}. \nonumber \]
Therefore
\[y_p=u_1x+u_2e^x =(-x)x+(-(x+1)e^{-x})e^x=-x^2-x-1, \nonumber \]
so the general solution of Equation \ref{eq:5.7.16} is
\[\label{eq:5.7.17} y=y_p+c_1x+c_2e^x=-x^2-x-1+c_1x+c_2e^x = -x^2-1+(c_1-1)x+c_2e^x.\]
However, since \(c_1\) is an arbitrary constant, so is \(c_1-1\); therefore, we improve the appearance of this result by renaming the constant and writing the general solution as
\[\label{eq:5.7.18} y= -x^2-1+c_1x+c_2e^x.\]
There’s nothing wrong with leaving the general solution of Equation \ref{eq:5.7.16} in the form Equation \ref{eq:5.7.17}; however, we think you’ll agree that Equation \ref{eq:5.7.18} is preferable. We can also view the transition from Equation \ref{eq:5.7.17} to Equation \ref{eq:5.7.18} differently. In this example the particular solution \(y_p=-x^2-x-1\) contained the term \(-x\), which satisfies the complementary equation. We can drop this term and redefine \(y_p=-x^2-1\), since \(-x^2-x-1\) is a solution of Equation \ref{eq:5.7.16} and \(x\) is a solution of the complementary equation; hence, \(-x^2-1=(-x^2-x-1)+x\) is also a solution of Equation \ref{eq:5.7.16}. In general, it is always legitimate to drop linear combinations of \(\{y_1,y_2\}\) from particular solutions obtained by variation of parameters. (See Exercise 5.7.36 for a general discussion of this question.) We’ll do this in the following examples and in the answers to exercises that ask for a particular solution. Therefore, don’t be concerned if your answer to such an exercise differs from ours only by a solution of the complementary equation.
Below is a video on verifying a solution to a differential equation and then solving it using variation of parameters.
Find a particular solution of
\[\label{eq:5.7.19} y''+3y'+2y={1\over 1+e^x}.\]
Then find the general solution.
Solution
The characteristic polynomial of the complementary equation
\[\label{eq:5.7.20} y''+3y'+2y=0\]
is \(p(r)=r^2+3r+2=(r+1)(r+2)\), so \(y_1=e^{-x}\) and \(y_2=e^{-2x}\) form a fundamental set of solutions of Equation \ref{eq:5.7.20}. We look for a particular solution of Equation \ref{eq:5.7.19} in the form
\[y_p=u_1e^{-x}+u_2e^{-2x}, \nonumber \]
where
\[\begin{aligned} \phantom{-}u_1'e^{-x}+\phantom{2}u_2'e^{-2x}&=0\\ -u_1'e^{-x}-2u_2'e^{-2x}&={1\over 1+e^x}.\end{aligned}\]
Adding these two equations yields
\[-u_2'e^{-2x}={1\over1+e^x},\quad \text{so} \quad u_2'=-{e^{2x}\over 1+e^x}. \nonumber \]
From the first equation,
\[u_1'=-u_2'e^{-x}={e^x\over 1+e^x}. \nonumber \]
Integrating by means of the substitution \(v=e^x\) and taking the constants of integration to be zero yields
\[u_1=\int{e^x\over 1+e^x}\,dx=\int {dv\over 1+v} =\ln(1+v)=\ln(1+e^x) \nonumber \]
and
\[\begin{aligned} u_2&=-\int{e^{2x}\over 1+e^x}\,dx=-\int {v\over 1+v}\,dv =\int\left[{1\over 1+v}-1\right]\,dv \\ &=\ln(1+v)-v=\ln(1+e^x)-e^x.\end{aligned}\]
Therefore
\[\begin{aligned} y_p&=u_1e^{-x}+u_2e^{-2x}\\ &=[\ln(1+e^x)]e^{-x}+\left[\ln(1+e^x)-e^x\right]e^{-2x},\end{aligned}\]
so
\[y_p=\left(e^{-x}+e^{-2x}\right)\ln(1+e^x)-e^{-x}. \nonumber \]
Since the last term on the right satisfies the complementary equation, we drop it and redefine
\[y_p=\left(e^{-x}+e^{-2x}\right)\ln(1+e^x). \nonumber \]
The general solution of Equation \ref{eq:5.7.19} is
\[y=y_p+c_1e^{-x}+c_2e^{-2x}=\left(e^{-x}+e^{-2x}\right)\ln(1+e^x) +c_1e^{-x}+c_2e^{-2x}. \nonumber \]
Solve the initial value problem
\[\label{eq:5.7.21} (x^2-1)y''+4xy'+2y={2\over x+1}, \quad y(0)=-1,\quad y'(0)=-5,\]
given that
\[y_1={1\over x-1}\quad\mbox{ and }\quad y_2={1\over x+1} \nonumber \]
are solutions of the complementary equation
\[(x^2-1)y''+4xy'+2y=0. \nonumber \]
Solution
We first use variation of parameters to find a particular solution of
\[(x^2-1)y''+4xy'+2y={2\over x+1} \nonumber \]
on \((-1,1)\) in the form
\[y_p={u_1\over x-1}+{u_2\over x+1}, \nonumber \]
where
\[\label{eq:5.7.22}\frac{u_{1}'}{x-1}+\frac{u_{2}'}{x+1}=0\]
\[-\frac{u_{1}'}{(x-1)^{2}}-\frac{u_{2}'}{(x+1)^{2}}=\frac{2}{(x+1)(x^{2}-1)}\nonumber\]
Multiplying the first equation by \(1/(x-1)\) and adding the result to the second equation yields
\[\label{eq:5.7.23} \left[{1\over x^2-1}-{1\over(x+1)^2}\right]u_2'={2\over(x+1)(x^2-1)}.\]
Since
\[\left[{1\over x^2-1}-{1\over(x+1)^2}\right]={(x+1)-(x-1)\over(x+1)(x^2-1)} ={2\over(x+1)(x^2-1)}, \nonumber \]
Equation \ref{eq:5.7.23} implies that \(u_2'=1\). From Equation \ref{eq:5.7.22},
\[u_1'=-{x-1\over x+1}u_2'=-{x-1\over x+1}. \nonumber \]
Integrating and taking the constants of integration to be zero yields
\[\begin{aligned} u_1&=-\int{x-1\over x+1}\,dx=-\int{x+1-2\over x+1}\,dx \\ &=\int\left[{2\over x+1}-1\right]\,dx=2\ln(x+1)-x\end{aligned}\]
and
\[u_2=\int\,dx=x. \nonumber \]
Therefore
\[\begin{aligned} y_p&={u_1\over x-1}+{u_2\over x+1}=\left[2\ln(x+1)-x\right]{1\over x-1} +x{1\over x+1} \\ &={2\ln(x+1)\over x-1}+x\left[{1\over x+1}-{1\over x-1}\right] ={2\ln(x+1)\over x-1}-{2x\over(x+1)(x-1)}.\end{aligned}\]
However, since
\[{2x\over(x+1)(x-1)}=\left[{1\over x+1}+{1\over x-1}\right] \nonumber \]
is a solution of the complementary equation, we redefine
\[y_p={2\ln(x+1)\over x-1}. \nonumber \]
Therefore the general solution of Equation \ref{eq:5.7.24} is
\[\label{eq:5.7.24} y={2\ln(x+1)\over x-1}+{c_1\over x-1}+{c_2\over x+1}.\]
Differentiating this yields
\[y'={2\over x^2-1}-{2\ln(x+1)\over(x-1)^2}-{c_1\over(x-1)^2}-{c_2\over(x+1)^2}. \nonumber \]
Setting \(x=0\) in the last two equations and imposing the initial conditions \(y(0)=-1\) and \(y'(0)=-5\) yields the system
\[\begin{aligned} -c_1+c_2&=-1\phantom{.}\\ -2-c_1-c_2&=-5.\end{aligned}\]
The solution of this system is \(c_1=2,\,c_2=1\). Substituting these into Equation \ref{eq:5.7.24} yields
\[\begin{aligned} y&={2\ln(x+1)\over x-1}+{2\over x-1}+{1\over x+1}\\ &={2\ln(x+1)\over x-1}+{3x+1\over x^2-1}\end{aligned}\]
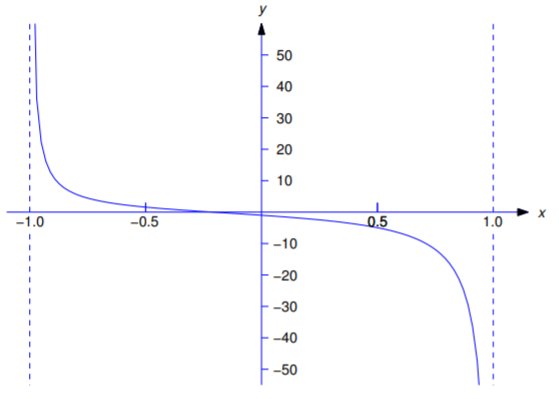
as the solution of Equation \ref{eq:5.7.21}. Figure 4.7.1 is a graph of the solution.
Below is a video on using variation of parameters to solve a differential equation.
We’ve now considered three methods for solving nonhomogeneous linear equations: undetermined coefficients, reduction of order, and variation of parameters. It’s natural to ask which method is best for a given problem. The method of undetermined coefficients should be used for constant coefficient equations with forcing functions that are linear combinations of polynomials multiplied by functions of the form \(e^{\alpha x}\), \(e^{\lambda x}\cos \omega x\), or \(e^{\lambda x}\sin \omega x\). Although the other two methods can be used to solve such problems, they will be more difficult except in the most trivial cases, because of the integrations involved.
If the equation isn’t a constant coefficient equation or the forcing function isn’t of the form just specified, the method of undetermined coefficients does not apply and the choice is necessarily between the other two methods. The case could be made that reduction of order is better because it requires only one solution of the complementary equation while variation of parameters requires two. However, variation of parameters will probably be easier if you already know a fundamental set of solutions of the complementary equation.