2.3: One-Sided Limits

Learning Objectives

• Define one-sided limits and provide examples.
• Explain the relationship between one-sided and two-sided limits.
• Define a vertical asymptote.

One-Sided Limits

Sometimes indicating that the limit of a function fails to exist at a point does not provide us with enough information about the behavior of the function at that particular point. To see this, we now revisit the function $g(x)=|x−2|/(x−2)$ introduced at the beginning of the section (see Figure $\PageIndex{1}$(b)). As we pick values of $x$ close to $2$, $g(x)$ does not approach a single value, so the limit as $x$ approaches $2$ does not exist—that is, $\displaystyle \lim_{x \to 2}g(x)$ DNE. However, this statement alone does not give us a complete picture of the behavior of the function around the $x$-value $2$. To provide a more accurate description, we introduce the idea of a one-sided limit. For all values to the left of $2$ (or the negative side of $2$), $g(x)=−1$. Thus, as $x$ approaches $2$ from the left, $g(x)$ approaches $−1$. Mathematically, we say that the limit as $x$ approaches $2$ from the left is $−1$. Symbolically, we express this idea as

$$\lim_{x \to 2^−}g(x)=−1. \nonumber$$

Similarly, as $x$ approaches $2$ from the right (or from the positive side), $g(x)$ approaches $1$. Symbolically, we express this idea as

$$\lim_{x \to 2^+}g(x)=1.\nonumber$$

We can now present an informal definition of one-sided limits.

Definition: One-sided Limits

We define two types of one-sided limits.

Limit from the left:

Let $f(x)$ be a function defined at all values in an open interval of the form $(z,a)$, and let $L$ be a real number. If the values of the function $f(x)$ approach the real number $L$ as the values of $x$ (where $x<a$) approach the number $a$, then we say that $L$ is the limit of $f(x)$ as $x$ approaches $a$ from the left. Symbolically, we express this idea as

$$\lim_{x \to a^−}f(x)=L. \nonumber$$

Limit from the right:

Let $f(x)$ be a function defined at all values in an open interval of the form $(a,c)$, and let $L$ be a real number. If the values of the function $f(x)$ approach the real number $L$ as the values of $x$ (where $x>a$) approach the number $a$, then we say that $L$ is the limit of $f(x)$ as $x$ approaches $a$ from the right. Symbolically, we express this idea as

$$\lim_{x \to a^+}f(x)=L. \nonumber$$

Example $\PageIndex{1}$: Evaluating One-Sided Limits

For the function $f(x)=\begin{cases}x+1, & \text{if }x<2\\ x^2−4, & \text{if }x≥2\end{cases}$, evaluate each of the following limits.

1. $\displaystyle \lim_{x \to 2^−}f(x)$
2. $\displaystyle \lim_{x \to 2^+}f(x)$

Solution

We can use tables of functional values again. Observe in Table $\PageIndex{6}$ that for values of $x$ less than $2$, we use $f(x)=x+1$ and for values of $x$ greater than $2$, we use $f(x)=x^2−4.$

Table $\PageIndex{6}$

$x$	$f(x)=x+1$	$x$	$f(x)=x^2-4$
1.9	2.9	2.1	0.41
1.99	2.99	2.01	0.0401
1.999	2.999	2.001	0.004001
1.9999	2.9999	2.0001	0.00040001
1.99999	2.99999	2.00001	0.0000400001

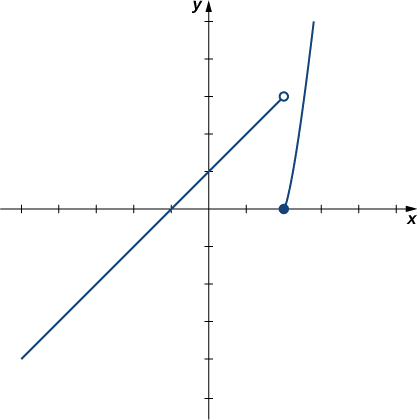
Based on this table, we can conclude that a. $\displaystyle \lim_{x \to 2^−}f(x)=3$ and b. $\displaystyle \lim_{x \to 2^+}f(x)=0$. Therefore, the (two-sided) limit of $f(x)$ does not exist at $x=2$. Figure $\PageIndex{7}$ shows a graph of $f(x)$ and reinforces our conclusion about these limits.

Figure $\PageIndex{7}$: The graph of $f(x)=\begin{cases}x+1, & \text{if }x<2\\ x^2−4, & \text{if }x≥2\end{cases}$ has a break at $x=2$.

Exercise $\PageIndex{1}$

Use a table of functional values to estimate the following limits, if possible.

1. $\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}$
2. $\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}$

Hint

Use $x$-values 1.9, 1.99, 1.999, 1.9999, 1.99999 to estimate $\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}$.

Use $x$-values 2.1, 2.01, 2.001, 2.0001, 2.00001 to estimate $\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}.$

(These tables are available from a previous Checkpoint problem.)

Solution a

a. $\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}=−4$

Solution b

$\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}=4$

Let us now consider the relationship between the limit of a function at a point and the limits from the right and left at that point. It seems clear that if the limit from the right and the limit from the left have a common value, then that common value is the limit of the function at that point. Similarly, if the limit from the left and the limit from the right take on different values, the limit of the function does not exist. These conclusions are summarized in Note.

Relating One-Sided and Two-Sided Limits

Let $f(x)$ be a function defined at all values in an open interval containing $a$, with the possible exception of $a$ itself, and let $L$ be a real number. Then,

$$\lim_{x \to a}f(x)=L \nonumber$$

if and only if $\displaystyle \lim_{x \to a^−}f(x)=L$ and $\displaystyle \lim_{x \to a^+} f(x)=L$.

Example $\PageIndex{2}$: Evaluating one sided limits

Let $f(x) = \left\{\begin{array}{cc} x & 0\leq x\leq 1 \\ 3-x & 1<x<2\end{array},\right.$ as shown in Figure 1.21. Find each of the following:

1. $\lim\limits_{x\to 1^-} f(x)$
2. $\lim\limits_{x\to 1^+} f(x)$
3. $\lim\limits_{x\to 1} f(x)$
4. $f(1)$
5. $\lim\limits_{x\to 0^+} f(x)$
6. $f(0)$
7. $\lim\limits_{x\to 2^-} f(x)$
8. $f(2)$

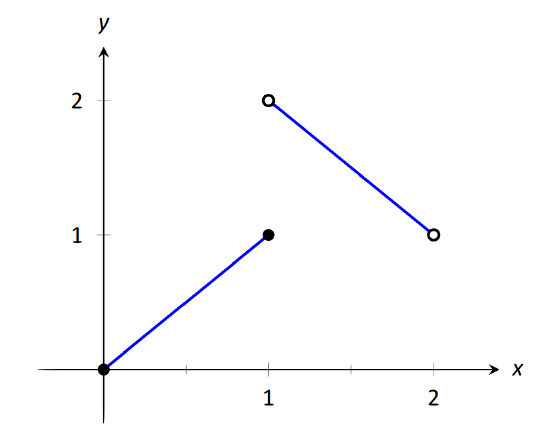
$\text{FIGURE 1.21}$: A graph of $f$ in Example 17.

Solution

For these problems, the visual aid of the graph is likely more effective in evaluating the limits than using $f$ itself. Therefore we will refer often to the graph.

1. As $x$ goes to 1 from the left, we see that $f(x)$ is approaching the value of 1. Therefore $\lim\limits_{x\to 1^-} f(x) =1.$
2. As $x$ goes to 1 from the right, we see that $f(x)$ is approaching the value of 2. Recall that it does not matter that there is an "open circle'' there; we are evaluating a limit, not the value of the function. Therefore $\lim\limits_{x\to 1^+} f(x)=2$.
3. The limit of $f$ as $x$ approaches 1 does not exist, as discussed in the first section. The function does not approach one particular value, but two different values from the left and the right.
4. Using the definition and by looking at the graph we see that $f(1) = 1$.
5. As $x$ goes to 0 from the right, we see that $f(x)$ is also approaching 0. Therefore $\lim\limits_{x\to 0^+} f(x)=0$. Note we cannot consider a left-hand limit at 0 as $f$ is not defined for values of $x<0$.
6. Using the definition and the graph, $f(0) = 0$.
7. As $x$ goes to 2 from the left, we see that $f(x)$ is approaching the value of 1. Therefore $\lim\limits_{x\to 2^-} f(x)=1.$
8. The graph and the definition of the function show that $f(2)$ is not defined.

Note how the left and right-hand limits were different at $x=1$. This, of course, causes the limit to not exist. The following theorem states what is fairly intuitive: the limit exists precisely when the left and right-hand limits are equal.

Theorem: Limits and One Sided Limits

Let $f$ be a function defined on an open interval $I$ containing $c$. Then $$\lim\limits_{x\to c}f(x) = L$$ if, and only if, $$\lim\limits_{x\to c^-}f(x) = L \quad \text{and} \quad \lim\limits_{x\to c^+}f(x) = L.$$

The phrase "if, and only if'' means the two statements are equivalent: they are either both true or both false. If the limit equals $L$, then the left and right hand limits both equal $L$. If the limit is not equal to $L$, then at least one of the left and right-hand limits is not equal to $L$ (it may not even exist).

One thing to consider in Examples 17 - 20 is that the value of the function may/may not be equal to the value(s) of its left/right-hand limits, even when these limits agree.

Example $\PageIndex{3}$: Evaluating limits of a piecewise-defined function

Let $f(x) = \left\{\begin{array}{cc} 2-x & 0<x<1 \\ (x-2)^2 & 1<x<2 \end{array},\right.$ as shown in Figure 1.22. Evaluate the following.

1. $\lim\limits_{x\to 1^-} f(x)$
2. $\lim\limits_{x\to 1^+} f(x)$
3. $\lim\limits_{x\to 1} f(x)$
4. $f(1)$
5. $\lim\limits_{x\to 0^+} f(x)$
6. $f(0)$
7. $\lim\limits_{x\to 2^-} f(x)$
8. $f(2)$

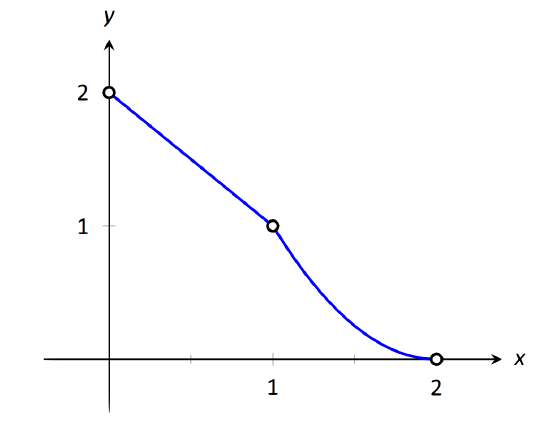
$\text{FIGURE 1.22}$: A graph of $f$ from Example 18.

Solution

Again we will evaluate each using both the definition of $f$ and its graph.

1. As $x$ approaches 1 from the left, we see that $f(x)$ approaches 1. Therefore $\lim\limits_{x\to 1^-} f(x)=1.$
2. As $x$ approaches 1 from the right, we see that again $f(x)$ approaches 1. Therefore $\lim\limits_{x\to 1+} f(x)=1$.
3. The limit of $f$ as $x$ approaches 1 exists and is 1, as $f$ approaches 1 from both the right and left. Therefore $\lim\limits_{x\to 1} f(x)=1$.
4. $f(1)$ is not defined. Note that 1 is not in the domain of $f$ as defined by the problem, which is indicated on the graph by an open circle when $x=1$.
5. As $x$ goes to 0 from the right, $f(x)$ approaches 2. So $\lim\limits_{x\to 0^+} f(x)=2$.
6. $f(0)$ is not defined as $0$ is not in the domain of $f$.
7. As $x$ goes to 2 from the left, $f(x)$ approaches 0. So $\lim\limits_{x\to 2^-} f(x)=0$.
8. $f(2)$ is not defined as 2 is not in the domain of $f$.

Example $\PageIndex{4}$: Evaluating limits of a piecewise-defined function

Let $f(x) = \left\{\begin{array}{cc} (x-1)^2 & 0\leq x\leq 2, x\neq 1\\ 1 & x=1\end{array},\right.$ as shown in Figure 1.23. Evaluate the following.

1. $\lim\limits_{x\to 1^-} f(x)$
2. $\lim\limits_{x\to 1^+} f(x)$
3. $\lim\limits_{x\to 1} f(x)$
4. $f(1)$

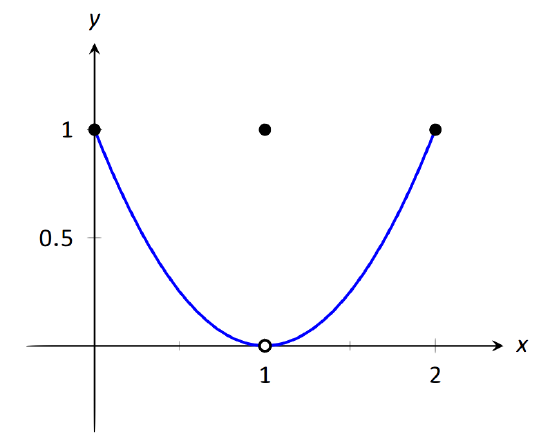
$\text{FIGURE 1.23}$: Graphing $f$ in Example 19.

It is clear by looking at the graph that both the left and right-hand limits of $f$, as $x$ approaches 1, is 0. Thus it is also clear that the limit is 0; i.e., $\lim\limits_{x\to 1} f(x) = 0$. It is also clearly stated that $f(1) = 1$.

Example $\PageIndex{5}$: Evaluating limits of a piecewise-defined function

Let $f(x) = \left\{\begin{array}{cc} x^2 & 0\leq x\leq 1 \\ 2-x & 1<x\leq 2\end{array},\right.$ as shown in Figure 1.24. Evaluate the following.

1. $\lim\limits_{x\to 1^-} f(x)$
2. $\lim\limits_{x\to 1^+} f(x)$
3. $\lim\limits_{x\to 1} f(x)$
4. $f(1)$

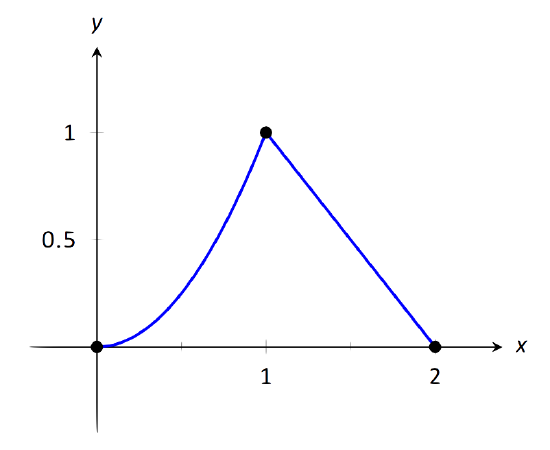
$\text{FIGURE 1.24}$: Graphing $f$ in Example 20.

Solution

It is clear from the definition of the function and its graph that all of the following are equal:

$$\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^+} f(x) =\lim\limits_{x\to 1} f(x) =f(1) = 1.$$

In Examples 17 - 20 we were asked to find both $\lim\limits_{x\to 1}f(x)$ and $f(1)$. Consider the following table:

$$\begin{array}{ccc} & \lim\limits_{x\to 1}f(x) & f(1) \\ \hline \text{Example 17} & \text{does not exist} & 1 \\ \text{Example 18} & 1 & \text{not defined} \\ \text{Example 19} & 0 & 1 \\ \text{Example 20} & 1 & 1 \\ \end{array}$$

Only in Example 20 do both the function and the limit exist and agree. This seems "nice;'' in fact, it seems "normal.'' This is in fact an important situation which we explore in the next section, entitled "Continuity.'' In short, a continuous function is one in which when a function approaches a value as $x\rightarrow c$ (i.e., when $\lim\limits_{x\to c} f(x) = L$), it actually attains that value at $c$. Such functions behave nicely as they are very predictable.

Example $\PageIndex{6}$: Using the Squeeze Theorem

Use the Squeeze Theorem to show that

$$\lim\limits_{x\to 0} \frac{\sin x}{x} = 1. \nonumber$$

Solution

We begin by considering the unit circle. Each point on the unit circle has coordinates $(\cos \theta,\sin \theta)$ for some angle $\theta$ as shown in Figure $\PageIndex{1}$. Using similar triangles, we can extend the line from the origin through the point to the point $(1,\tan \theta)$, as shown. (Here we are assuming that $0\leq \theta \leq \pi/2$.Later we will show that we can also consider $\theta \leq 0$.)

Figure $\PageIndex{1}$: The unit circle and related triangles.

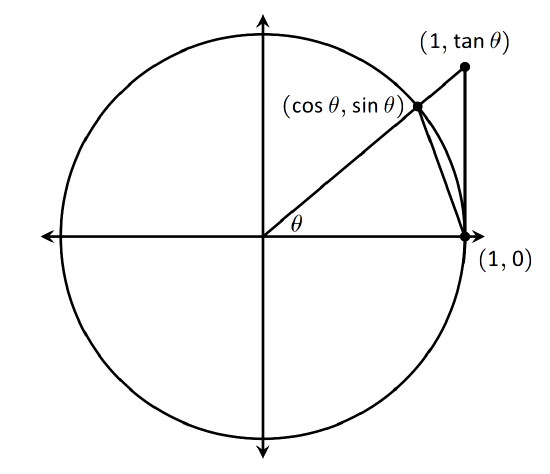
Figure 1.19 shows three regions have been constructed in the first quadrant, two triangles and a sector of a circle, which are also drawn below. The area of the large triangle is $\frac12\tan\theta$; the area of the sector is $\theta/2$; the area of the triangle contained inside the sector is $\frac12\sin\theta$. It is then clear from the diagram that

Multiply all terms by $\frac{2}{\sin \theta}$, giving

$$\frac{1}{\cos\theta} \geq \frac{\theta}{\sin \theta} \geq 1.$$

Taking reciprocals reverses the inequalities, giving

$$\cos \theta \leq \frac{\sin \theta}{\theta} \leq 1.$$

(These inequalities hold for all values of $\theta$ near 0, even negative values, since $\cos (-\theta) = \cos \theta$ and $\sin (-\theta) = -\sin \theta$.)

Now take limits.

$$\lim\limits_{\theta\to 0} \cos \theta \leq \lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta} \leq \lim\limits_{\theta\to 0} 1$$

$$\cos 0 \leq \lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta} \leq 1$$

$$1 \leq \lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta} \leq 1$$

Clearly this means that $\lim\limits_{\theta\to 0} \frac{\sin\theta}{\theta}=1$

Two notes about the previous example are worth mentioning. First, one might be discouraged by this application, thinking "I would never have come up with that on my own. This is too hard!'' Don't be discouraged; within this text we will guide you in your use of the Squeeze Theorem. As one gains mathematical maturity, clever proofs like this are easier and easier to create.

Second, this limit tells us more than just that as $x$ approaches 0, $\sin(x)/x$ approaches 1. Both $x$ and $\sin x$ are approaching 0, but the ratio of $x$ and $\sin x$ approaches 1, meaning that they are approaching 0 in essentially the same way. Another way of viewing this is: for small $x$, the functions $y=x$ and $y=\sin x$ are essentially indistinguishable.

We include this special limit, along with three others, in the following theorem.

Theorem: Special Limits

1. $\lim\limits_{x\to 0} \frac{\sin x}{x} = 1$
2. $\lim\limits_{x\to 0} \frac{\cos x-1}{x} = 0$

A short word on how to interpret the latter three limits. We know that as $x$ goes to 0, $\cos x$ goes to 1. So, in the second limit, both the numerator and denominator are approaching 0. However, since the limit is 0, we can interpret this as saying that "$\cos x$ is approaching 1 faster than $x$ is approaching 0.''

Example $\PageIndex{7}$: Using Special Limits

Evaluate the following limit:

$$\lim\limits_{x\to 0}\frac{\sin 2x}{3x}. \nonumber$$

Solution

The answer here is not going to be 1 since the numbers in front of each x do not match. We need the bottom to be 3x. We can do this by multiplying the numerator and denominator by the fraction $\frac{1}{2x}$.

$$\lim\limits_{x\to 0}\frac{\sin 2x}{3x}=\lim\limits_{x\to 0}\frac{(\frac{1}{2x})\sin 2x}{(\frac{1}{2x})3x}=\lim\limits_{x\to 0}\frac{\frac{\sin 2x}{2x}}{\frac{3}{2}}=\frac{2}{3} \lim\limits_{x\to 0}\frac{\sin 2x}{2x}=\frac{2}{3}(1)=\frac{2}{3}. \nonumber$$