6.2: Polygons
- Page ID
- 51013
Below is a table of polygons. There are an infinite amount of polygons, but the following are the shapes taught in elementary school.
|
Number of Sides |
Name |
Irregular Polygon |
Regular Polygon |
|---|---|---|---|
|
3 sides |
Triangle |
 |
 |
|
4 sides |
Quadrilateral |
 |
 |
|
5 sides |
Pentagon |
|
 |
|
6 sides |
Hexagon |
|
 |
|
8 sides |
Octagon |
 |
 |
Definition: Regular Polygon
A shape whose sides have the same length and whose angles have the same measure.
Definition: Irregular Polygon
A shape whose sides differ in length or have angles of different measure.
Hierarchy of Polygons

Polygon Definitions
Definition: Kite
A quadrilateral with two consecutive sides having equal lengths and the other two sides also have equal lengths.
Definition: Trapezoid
A quadrilateral with at least one pair of opposite sides parallel.
Definition: Isosceles Trapezoid
A trapezoid with both angles next to one of the parallel sides having the same size.
Definition: Parallelogram
A trapezoid with pairs of opposite sides parallel.
Definition: Rectangle
A parallelogram with a right angle.
Definition: Rhombus
A quadrilateral with all sides being the same.
Definition: Square
A rectangle that has four equal sides.
Types of Triangles
|
Name |
Definition |
Triangle |
|---|---|---|
|
SIDES |
||
|
Equilateral |
All three sides are equal |
|
|
Isosceles |
Only two sides are equal |
|
|
Scalene |
All three sides are different in length |
 |
|
ANGLES |
||
|
Acute |
Each angle is less than 900 |
 |
|
Right |
One angle is 900 |
 |
|
Obtuse |
One angle is more than 900 |
 |
Partner Activity 1
Draw the following triangles
- Isosceles right triangle
- Scalene obtuse triangle
- Equilateral right triangle
Partner Activity 2
- Is a rectangle a square? Is a square a rectangle?
- Multiple Choice: Which one is NOT a name for the figure below?
- Polygon
- Quadrilateral
- Parallelogram
- Trapezoid

-
What is the difference between a regular and irregular polygon?
Facts about Angles

- Angles in a triangle add up to 1800
- An angle forming a straight line is also 1800
- Any quadrilateral (4-sided figure) is 3600
- Angles which round a point add up to 3600
- The two base angles of an isosceles triangle are equal
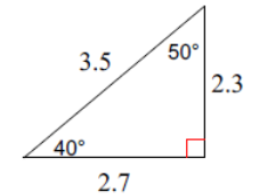
Why does a triaangle add up to \(180^{\circ }\)
A full circle is \(360^{\circ}\). Half of a circle, called a semicircle, would then be \(180^{\circ }\). The diameter (a line which passes through the center of the circle) of the semicircle is then also \(180^{\circ }\). Therefore, all straight lines are \(180^{\circ }\). See the figure below. Knowing that all straight lines are \(180^{\circ }\), we look at the figure below of the line and triangle.

Since a line is \(180^{\circ }\), we know that angles \(A_1\), B, and \(C_1\) must add up to \(180^{\circ }\). A theorem (proven statement) in Geometry states that alternate (opposite sides) interior angles are congruent (equal). Angles \(A_1\) and \(A_2\) are alternate interior, cut by the transversal (line) connecting angle \(A_2\) to the straight line. Angles \(C_1\) and \(C_2\) follow a similar approach.
Since the measures of angles \(A_{1}=A_{2}\), \(C_{1}=C_{2}\), and \(A_{1}+B+C_{1}=180\), then by substitution, \(A_{2}+B+C_{2}=180\). Therefore, triangle \(A_{2} B C_{2}\) adds up to \(180^{\circ }\).
Partner Activity 3
The sum of the interior angles of any polygon is represented by: \(180(n-2)\).
- Find the sum of the interior angles of a triangle, using the formula.
- Find the sum of the interior angles of a pentagon, using the formula.
- Find the sum of the interior angles of a 15-sided polygon, using the formula.
- What is the sum of the EXTERIOR angles of a pentagon?
Complementary and Supplementary Angles
Definition: Complementary Angles
Complementary angles are any two angles with a sum of 900. See angles C and D below.

Definition: Supplementary Angles
Supplementary angles are any two angles with a sum of 1800. See angles A and B below.

Partner Activity 4
- You have two supplementary angles. One angle is 300. What is the measure of the other angle?
- One angle is complementary to another angle. The first one is 490. What is the measure of the second angle?
Practice Problems
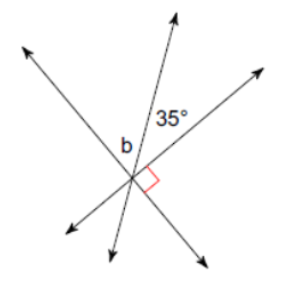
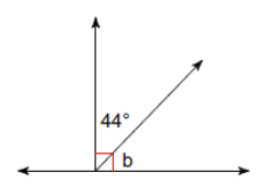
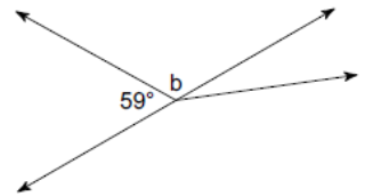
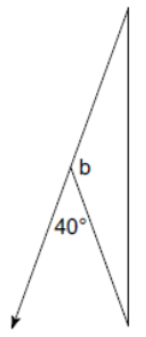
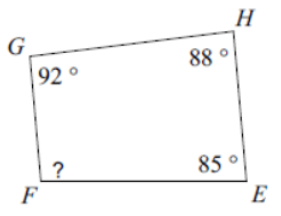
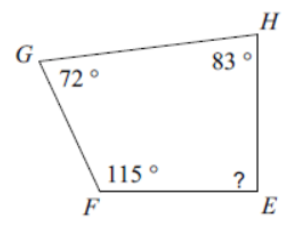
(Problems 1 – 4) Find the measure of angle b.
(Problems 5 – 6) Find the measure of each angle indicated.
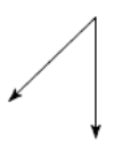
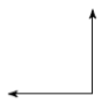
(Problems 7 – 10) Classify each angle as acute, obtuse, right or straight.
-
\(121^{\circ}\)
-
\(180^{\circ}\)
-
-
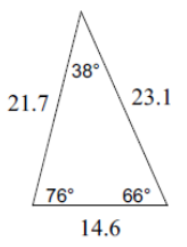
(Problems 11 – 12) Classify each triangle by its angles.
(Problems 13 – 14) Classify each triangle by its angles and sides.
(Problems 15 – 16) Sketch an example of the type of triangle described.
-
Acute Isosceles
-
Right Obtuse
(Problems 17 – 18) Write the name of each polygon.
(Problems 19 – 22) Find the interior angle sum for each polygon. Round your answer to the nearest tenth, if necessary.
(Problems 23 – 26) State if the polygon is regular or irregular.