2.1E: Exercises - Solving Linear Inequalities in One Variable
( \newcommand{\kernel}{\mathrm{null}\,}\)
Determine whether or not the given value is a solution.
- 5x−1<−2;x=−1
- −3x+1>−10;x=1
- 2x−3<−5;x=1
- 5x−7<0;x=2
- 9y−4≥5;y=1
- −6y+1≤3;y=−1
- Answer
-
1. Yes
3. No
5. Yes
Graph all solutions on a number line and provide the corresponding interval notation.
- 3x+5>−4
- 2x+1>−1
- 6−a≤6
- −2a+5>5
- 5x+63≤7
- 4x+116≤12
- 2(3x+14)<−2
- 5(2y+9)>−15
- 5x−2(x−3)<3(2x−1)
- 3(2x−1)−10>4(3x−2)−5x
- Answer
-
1. (−3,∞);
 Figure 1.8.13
Figure 1.8.133. [0,∞);

Figure 1.8.14 5. (−∞,3];

Figure 1.8.15 7. (−∞,−5);
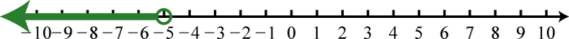
Figure 1.8.16 9. (3,∞);
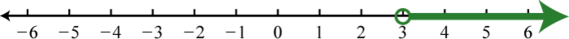
Figure 1.8.17
Footnotes
138Linear expressions related with the symbols ≤,<,≥, and >.
139A real number that produces a true statement when its value is substituted for the variable.
140Properties used to obtain equivalent inequalities and used as a means to solve them.
141Inequalities that share the same solution set.
142Two or more inequalities in one statement joined by the word “and” or by the word “or.”

