6.4: Present Value of Annuities and Installment Payment
- Page ID
- 147342
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section, you will learn to:
- Find the present value of an annuity.
- Find the amount of installment payment on a loan.
- Find the outstanding balance on a loan.
Before you get started, take this prerequisite quiz.
1. What will the final amount be in 4 years if $8,000 is invested at 9.2% compounded monthly?
- Click here to check your answer
-
\($11,542.53\)
If you missed this problem, review Section 6.2. (Note that this will open in a new window.)
2. How much should be invested at 10.3% compounded quarterly for it to amount to $10,000 in 6 years?
- Click here to check your answer
-
\($5,432.55\)
If you missed this problem, review Section 6.2. (Note that this will open in a new window.)
3. Find the future value of an annuity of $200 per month for 5 years at 6% compounded monthly.
- Click here to check your answer
-
\($13,954.01\)
If you missed this problem, review Section 6.3. (Note that this will open in a new window.)
4. How much money should be deposited at the end of each month in an account paying 7.5% for it to amount to $10,000 in 5 years?
- Click here to check your answer
-
\($137.88\)
If you missed this problem, review Section 6.3. (Note that this will open in a new window.)
PRESENT VALUE OF AN ANNUITY
In the previous two sections, we learned to find the future value of a lump sum and the future value of an annuity. With these two concepts in hand, we will now learn to amortize a loan, and to find the present value of an annuity.
The present value of an annuity is the amount of money we would need now in order to be able to make the payments in the annuity in the future. In other words, the present value is the value now of a future stream of payments.
We start by breaking this down step by step to understand the concept of the present value of an annuity. After that, the examples provide a more efficient way to do the calculations by working with concepts and calculations we have already explored in the last two sections.
Suppose Carlos owns a small business and employs an assistant manager to help him run the business. Assume it is January 1 now. Carlos plans to pay his assistant manager a $1000 bonus at the end of this year and another $1000 bonus at the end of the following year. Carlos’ business had good profits this year so he wants to put the money for his assistant’s future bonuses into a savings account now. The money he puts in now will earn interest at the rate of 4% per year compounded annually while in the savings account.
How much money should Carlos put into the savings account now so that he will be able to withdraw $1000 one year from now and another $1000 two years from now?
At first, this sounds like a sinking fund. But it is different. In a sinking fund, we put money into the fund with periodic payments to save to accumulate to a specified lump sum that is the future value at the end of a specified time period.
In this case we want to put a lump sum into the savings account now, so that lump sum is our principal, \(\mathrm{P}\). Then we want to withdraw that amount as a series of period payments; in this case the withdrawals are an annuity with $1000 payments at the end of each of two years.
We need to determine the amount we need in the account now, the present value, to be able to make withdraw the periodic payments later.
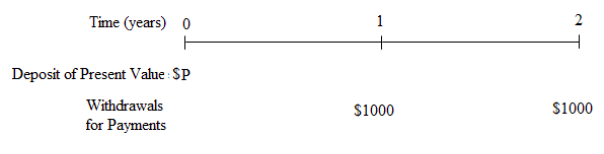
We use the compound interest formula from Section 6.2 with \(r\) = 0.04 and \(n\) = 1 for annual compounding to determine the present value of each payment of $1000.
Consider the first payment of $1000 at the end of year 1. Let P1 be its present value
\[\$ 1000=P_{1}(1.04)^{1} \text { so } P_{1}=\$ 961.54 \nonumber\]
Now consider the second payment of $1000 at the end of year 2. Let P2 is its present value
\[\$ 1000=P_{2}(1.04)^{2} \text { so } P_{2}=\$ 924.56 \nonumber\]
To make the $1000 payments at the specified times in the future, the amount that Carlos needs to deposit now is the present value \(P=P_{1}+P_{2}=\$ 961.54+\$ 924.56=\$ 1886.10\)
The calculation above was useful to illustrate the meaning of the present value of an annuity.
But it is not an efficient way to calculate the present value. If we were to have a large number of annuity payments, the step by step calculation would be long and tedious.
Example \(\PageIndex{1}\) investigates and develops an efficient way to calculate the present value of an annuity, by relating the future (accumulated) value of an annuity and its present value.
Suppose you have won a lottery that pays $1,000 per month for the next 20 years. But, you prefer to have the entire amount now. If the interest rate is 8%, how much will you accept?
Solution
This classic present value problem needs our complete attention because the rationalization we use to solve this problem will be used again in the problems to follow.
Consider, for argument purposes, that two people Mr. Cash, and Mr. Credit have won the same lottery of $1,000 per month for the next 20 years. Mr. Credit is happy with his $1,000 monthly payment, but Mr. Cash wants to have the entire amount now.
Our job is to determine how much Mr. Cash should get. We reason as follows:
If Mr. Cash accepts P dollars, then the P dollars deposited at 8% for 20 years should yield the same amount as the $1,000 monthly payments for 20 years. In other words, we are comparing the future values for both Mr. Cash and Mr. Credit, and we would like the future values to equal.
Since Mr. Cash is receiving a lump sum of \(x\) dollars, its future value is given by the lump sum formula, and it is
\[\mathrm{A}=\mathrm{P}(1+.08 / 12)^{240} \nonumber\]
Since Mr. Credit is receiving a sequence of payments, or an annuity, of $1,000 per month, its future value is given by the annuity formula This value is
\[\mathrm{A}=\frac{\$ 1000\left[(1+.08 / 12)^{240}-1\right]}{.08 / 12} \nonumber\]
The only way Mr. Cash will agree to the amount he receives is if these two future values are equal. So we set them equal and solve for the unknown.
\[\begin{array}{l}
\mathrm{P}(1+.08 / 12)^{240}=\frac{\$ 1000\left[(1+.08 / 12)^{240}-1\right]}{.08 / 12} \\
\mathrm{P}=\frac{\frac{\$ 1000\left[(1+.08 / 12)^{240}-1\right]}{.08 / 12}}{(1+.08 / 12)^{240}} \\
\mathrm{P}=\$ 119,554.36
\end{array} \nonumber\]
The present value of an ordinary annuity of $1,000 each month for 20 years at 8% is $119,554.36
The reader should also note that if Mr. Cash takes his lump sum of \(\mathrm{P}\) = $119,554.36 and invests it at 8% compounded monthly, he will have an accumulated value of \(\mathrm{A}\)=$589,020.41 in 20 years.
If a person or business needs to buy or pay for something now (a car, a home, college tuition, equipment for a business) but does not have the money, they can borrow the money as a loan.
They receive the loan amount called the principal (or present value) now and are obligated to pay back the principal in the future over a stated amount of time (term of the loan), as regular periodic payments with interest.
We can see the formula begin to develop in the example above.
If a payment of \(m\) dollars is made in an account \(n\) times a year at an interest \(r\), then the present value \(\mathrm{P}\) of the annuity after \(t\) years is
\[\mathbf{P}(\mathbf{1}+\mathbf{r} / \mathbf{n})^{\mathbf{n} \mathbf{t}}=\frac{\mathbf{m}\left[(\mathbf{1}+\mathbf{r} / \mathbf{n})^{\mathbf{n} \mathbf{t}}-\mathbf{1}\right]}{\mathbf{r} / \mathbf{n}}\]
When used for a loan, the amount \(\mathrm{P}\) is the loan amount, and \(m\) is the periodic payment needed to repay the loan over a term of \(t\) years with \(n\) payments per year.
Note that the formula assumes that the payment period is the same as the compounding period. If these are not the same, then this formula does not apply.
You determine that you can afford $550 per month for a car. At the dealership, the finance department offers you a 3-year loan with a 7% interest rate, compounded monthly.
- What is the highest priced car you can afford in this scenario?
- How much will you pay over the 3 years?
- What is the difference between the answers for part a and part b, and what does it represent?
Solution
a. Using the formula above, we are looking for the total amount of the loan, or \(P\). We know that \(m=550\), \(r=0.07\), \(n=12\), and \(t=3\).
\(\mathbf{P}(\mathbf{1}+\mathbf{0.07} / \mathbf{12})^{\mathbf{(12 \cdot 3)}}=\frac{\mathbf{550}\left[(\mathbf{1}+\mathbf{0.07} / \mathbf{12})^{\mathbf{(12 \cdot 3)}}-\mathbf{1}\right]}{\mathbf{0.07} / \mathbf{12}}\)
\(\mathbf{P}=\frac{\frac{\mathbf{550}\left[(\mathbf{1}+\mathbf{0.07} / \mathbf{12})^{\mathbf{(12 \cdot 3)}}-\mathbf{1}\right]}{\mathbf{0.07} / \mathbf{12}}}{(\mathbf{1}+\mathbf{0.07} / \mathbf{12})^{\mathbf{(12 \cdot 3)}}}\)
\(P=17812.55545\)
You can take a loan of $17,812.55 to pay off within 3 years.
b. Over the course of 3 years, you would pay $550 every month, 12 months each year, for 3 years.
Total paid \(=$550 \cdot 12 \cdot 3=$19,800\).
c. The difference between $17,812.55 as the purchase price and $19,800 as the repayment price is \($19800-$17812.55=$1987.45\). This means that you'll pay $1,987.45 in interest over the 3 years.
Alternate Method to find Present Value of an Annuity
We should note that many finite mathematics and finance books develop the formula for the present value of an annuity differently.
Instead of using the formula:
\[\mathrm{P}(1+\mathrm{r} / \mathrm{n})^{\mathrm{nt}}=\frac{\mathrm{m}\left[(1+\mathrm{r} / \mathrm{n})^{\mathrm{nt}}-1\right]}{\mathrm{r} / \mathrm{n}} \label{8.4.1}\]
and solving for the present value \(\mathrm{P}\) after substituting the numerical values for the other items in the formula, many textbooks first solve the formula for \(\mathrm{P}\) in order to develop a new formula for the present value. Then the numerical information can be substituted into the present value formula and evaluated, without needing to solve algebraically for \(\mathrm{P}\).
Starting with formula \ref{8.4.1}: \(\mathrm{P}(1+\mathrm{r} / \mathrm{n})^{\mathrm{nt}}=\frac{\mathrm{m}\left[(1+\mathrm{r} / \mathrm{n})^{\mathrm{nt}}-1\right]}{\mathrm{r} / \mathrm{n}}\)
Divide both sides by \((1+r / n)^{n t}\) to isolate \(\mathrm{P}\), and simplify
\[P=\frac{m\left[(1+r / n)^{n t}-1\right]}{r / n} \cdot \frac{1}{(1+r / n)^{n t}} \nonumber\]
\[P=\frac{m\left[1-(1+r / n)^{-n t}\right]}{r / n} \label{8.4.2} \]
The authors of this book believe that it is easier to use formula \ref{8.4.1} at the top of this page and solve for \(\mathrm{P}\) or \(m\) as needed. In this approach there are fewer formulas to understand, and many students find it easier to learn. In the problems the rest of this chapter, when a problem requires the calculation of the present value of an annuity, formula \ref{8.4.1} will be used.
However, formula \ref{8.4.2} is ideal when used to solve for \(t\), and some people prefer to use this formula to find present value. It is a mathematically correct option to do so. Note that if you choose to use formula \ref{8.4.2}, you need to be careful with the negative exponents in the formula.
INSTALLMENT PAYMENTS ON A LOAN
Example \(\PageIndex{3}\) examines how to calculate the loan payment, using reasoning similar to Example \(\PageIndex{1}\).
Daria purchased a truck costing $45,000 and accepted a 60-month loan at an interest rate of 9%, compounded monthly.
- Find the monthly installment payments.
- How much will she pay over the course of the loan?
- How much interest will she pay over the course of the loan?
Solution
a. The monthly installment payments can be found in a similar process to finding the principal in Example \(\PageIndex{2}\). Note that 60 months is the same as 5 years. We can use \(t=5\) or we can use \(nt=60\).
\[\begin{array}{l}
\$ 45,000(1+.09 / 12)^{60}=\frac{m\left[(1+.09 / 12)^{60}-1\right]}{.09 / 12} \\
\end{array} \nonumber\]
We then multiply both sides by the denominator:
\[\begin{array}{l}
(\$ 45,000(1+.09 / 12)^{60})(\frac{.09}{12})=m\left[(1+.09 / 12)^{60}-1\right] \\
\end{array} \nonumber\]
Finally dividing by the entire quantity that is multiplied to the m leaves:
\[\begin{array}{l}
\frac{(\$ 45,000(1+.09 / 12)^{60})(\frac{.09}{12})}{\left[(1+.09 / 12)^{60}-1\right] }=m\\
\$ 934.13=m
\end{array} \nonumber\]
Therefore, the monthly payment needed to repay the loan is $934.13 for five years.
b. Over the course of the loan, she would pay $934.13 every month for 60 months.
Total paid \(=$934.13 \cdot 60=$56047.80\).
c. To find interest, we find the difference between purchase price and repayment price. \($56047.80-$45000=$16047.80\), so she will pay \($16047.80\) in interest over the course of the loan.
OUTSTANDING BALANCE ON A LOAN
One of the most common problems deals with finding the balance owed at a given time during the life of a loan. Suppose a person buys a house and amortizes the loan over 30 years, but decides to sell the house a few years later. At the time of the sale, he is obligated to pay off his lender, therefore, he needs to know the balance he owes. Since most long term loans are paid off prematurely, we are often confronted with this problem.
To find the outstanding balance of a loan at a specified time, we need to find the present value \(\mathrm{P}\) of all future payments that have not yet been paid. In this case t does not represent the entire term of the loan. Instead:
- \(t\) represents the time that still remains on the loan
- \(nt\) represents the total number of future payments.
If the problem does not directly state the amount of time still remaining in the term of the loan, then it must be calculated FIRST using \(t\) = [original term of loan] - [time already passed since the start date of the loan].
Mr. Jackson bought his house in 1995, and financed the loan for 30 years at an interest rate of 7.8%. His monthly payment was $1260. In 2015, Mr. Jackson decides to pay off the loan. Find the balance of the loan he still owes.
Solution
The reader should note that the original amount of the loan is not mentioned in the problem. That is because we don't need to know that to find the balance.
The original loan was for 30 years. 20 years have passed so there are 10 years still remaining. 12(10) = 120 payments still remain to be paid on this loan.
As for the bank or lender is concerned, Mr. Jackson is obligated to pay $1260 each month for 10 more years; he still owes a total of 120 payments. But since Mr. Jackson wants to pay it all off now, we need to find the present value \(\mathrm{P}\) at the time of repayment of the remaining 10 years of payments of $1260 each month. Using the formula we get for the present value of an annuity, we get
\[\begin{aligned}
\mathrm{P}(1+.078 / 12)^{120} &=\frac{\left.\$ 1260\left[(1+.078 / 12)^{120}-1\right)\right]}{(.078 / 12)} \\
\mathrm{P}(2.17597) &=\$ 227957.85 \\
\mathrm{P} &=\$ 104761.48
\end{aligned} \nonumber\]
If a loan has a payment of \(m\) dollars made \(n\) times a year at an interest \(r\), then the outstanding value of the loan when there are \(t\) years still remaining on the loan is given by \(\mathrm{P}\):
\[\mathbf{P}(\mathbf{1}+\mathbf{r} / \mathbf{n})^{\mathbf{n} \mathbf{t}}=\frac{\mathbf{m}\left[(\mathbf{1}+\mathbf{r} / \mathbf{n})^{\mathbf{n} \mathbf{t}}-\mathbf{1} |\right.}{\mathbf{r} / \mathbf{n}}\]
IMPORTANT: Note that \(t\) is not the original term of the loan but instead \(t\) is the amount of time still remaining in the future; \(nt\) is the number of payments still remaining in the future
If the problem does not directly state the amount of time still remaining in the term of the loan, then it must be calculated BEFORE using the above formula as \(t\) = [original term of loan] - [time already passed since the start date of the loan].
Note that there are other methods to find the outstanding balance on a loan, but the method illustrated above is generally considered the easiest.


