5.4: Power Functions and Polynomial Functions

Learning Objectives

• Identify power functions.
• Identify polynomial functions.
• Identify the degree and leading coefficient of polynomial functions.

Suppose a certain species of bird thrives on a small island. Its population over the last few years is shown in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\)

Year	2009	2010	2011	2012	2013
Bird Population	800	897	992	1,083	1,169

The population can be estimated using the function \(P(t)=−0.3t^3+97t+800\), where \(P(t)\) represents the bird population on the island \(t\) years after 2009. We can use this model to estimate the maximum bird population and when it will occur. We can also use this model to predict when the bird population will disappear from the island. In this section, we will examine functions that we can use to estimate and predict these types of changes.

Figure \(\PageIndex{1}\): (credit: Jason Bay, Flickr)

Identifying Power Functions

In order to better understand the bird problem, we need to understand a specific type of function. A power function is a function with a single term that is the product of a real number, a coefficient, and a variable raised to a fixed real number. (A number that multiplies a variable raised to an exponent is known as a coefficient.)

As an example, consider functions for area or volume. The function for the area of a circle with radius \(r\) is

\[A(r)={\pi}r^2 \nonumber\]

and the function for the volume of a sphere with radius \(r\) is

\[V(r)=\dfrac{4}{3}{\pi}r^3 \nonumber\]

Both of these are examples of power functions because they consist of a coefficient, \({\pi}\) or \(\dfrac{4}{3}{\pi}\), multiplied by a variable \(r\) raised to a power.

Definition: Power Function

A power function is a function that can be represented in the form

\[f(x)=kx^p \label{power}\]

where \(k\) and \(p\) are real numbers, and \(k\) is known as the coefficient.

Q&A: Is \(f(x)=2^x\) a power function?

No. A power function contains a variable base raised to a fixed power (Equation \ref{power}). This function has a constant base raised to a variable power. This is called an exponential function, not a power function. This function will be discussed later.

Example \(\PageIndex{1}\): Identifying Power Functions

Which of the following functions are power functions?

\[\begin{align*} f(x)&=1 &\text{Constant function} \\f(x)&=x &\text{Identify function} \\f(x)&=x^2 &\text{Quadratic function} \\ f(x)&=x^3 &\text{Cubic function} \\ f(x)&=\dfrac{1}{x} &\text{Reciprocal function} \\f(x)&=\dfrac{1}{x^2} &\text{Reciprocal squared function} \\ f(x)&=\sqrt{x} &\text{Square root function} \\ f(x)&=\sqrt[3]{x} &\text{Cube root function} \end{align*}\]

Solution

All of the listed functions are power functions.

The constant and identity functions are power functions because they can be written as \(f(x)=x^0\) and \(f(x)=x^1\) respectively.

The quadratic and cubic functions are power functions with whole number powers \(f(x)=x^2\) and \(f(x)=x^3\).

The reciprocal and reciprocal squared functions are power functions with negative whole number powers because they can be written as \(f(x)=x^{−1}\) and \(f(x)=x^{−2}\).

The square and cube root functions are power functions with fractional powers because they can be written as \(f(x)=x^{1/2}\) or \(f(x)=x^{1/3}\).

Exercise \(\PageIndex{1}\)

Which functions are power functions?

• \(f(x)=2x^2⋅4x^3\)
• \(g(x)=−x^5+5x^3−4x\)
• \(h(x)=\frac{2x^5−1}{3x^2+4}\)

Answer

\(f(x)\) is a power function because it can be written as \(f(x)=8x^5\). The other functions are not power functions.

Identifying Polynomial Functions

An oil pipeline bursts in the Gulf of Mexico, causing an oil slick in a roughly circular shape. The slick is currently 24 miles in radius, but that radius is increasing by 8 miles each week. We want to write a formula for the area covered by the oil slick by combining two functions. The radius \(r\) of the spill depends on the number of weeks \(w\) that have passed. This relationship is linear.

\[r(w)=24+8w \nonumber\]

We can combine this with the formula for the area A of a circle.

\[A(r)={\pi}r^2 \nonumber\]

Composing these functions gives a formula for the area in terms of weeks.

\[ \begin{align*} A(w)&=A(r(w)) \\ &=A(24+8w) \\ & ={\pi}(24+8w)^2 \end{align*}\]

Multiplying gives the formula.

\[A(w)=576{\pi}+384{\pi}w+64{\pi}w^2 \nonumber\]

This formula is an example of a polynomial function. A polynomial function consists of either zero or the sum of a finite number of non-zero terms, each of which is a product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.

Definition: Polynomial Functions

Let \(n\) be a non-negative integer. A polynomial function is a function that can be written in the form

\[f(x)=a_nx^n+...+a_2x^2+a_1x+a_0 \label{poly}\]

This is called the general form of a polynomial function. Each \(a_i\) is a coefficient and can be any real number. Each product \(a_ix^i\) is a term of a polynomial function.

Example \(\PageIndex{4}\): Identifying Polynomial Functions

Which of the following are polynomial functions?

• \(f(x)=2x^3⋅3x+4\)
• \(g(x)=−x(x^2−4)\)
• \(h(x)=5\sqrt{x}+2\)

Solution

The first two functions are examples of polynomial functions because they can be written in the form of Equation \ref{poly}, where the powers are non-negative integers and the coefficients are real numbers.

• \(f(x)\) can be written as \(f(x)=6x^4+4\).
• \(g(x)\) can be written as \(g(x)=−x^3+4x\).
• \(h(x)\) cannot be written in this form and is therefore not a polynomial function.

Identifying the Degree and Leading Coefficient of a Polynomial Function

Because of the form of a polynomial function, we can see an infinite variety in the number of terms and the power of the variable. Although the order of the terms in the polynomial function is not important for performing operations, we typically arrange the terms in descending order of power, or in general form. The degree of the polynomial is the highest power of the variable that occurs in the polynomial; it is the power of the first variable if the function is in general form. The leading term is the term containing the highest power of the variable, or the term with the highest degree. The leading coefficient is the coefficient of the leading term.

Terminology of Polynomial Functions

We often rearrange polynomials so that the powers are descending.

Figure \(\PageIndex{7}\)

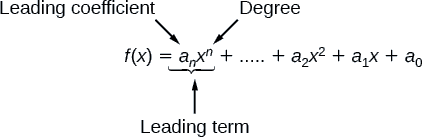
When a polynomial is written in this way, we say that it is in general form.

How To: Given a polynomial function, identify the degree and leading coefficient

1. Find the highest power of \(x\) to determine the degree function.
2. Identify the term containing the highest power of \(x\) to find the leading term.
3. Identify the coefficient of the leading term.

Example \(\PageIndex{5}\): Identifying the Degree and Leading Coefficient of a Polynomial Function

Identify the degree, leading term, and leading coefficient of the following polynomial functions.

\(f(x)=3+2x^2−4x^3\)

\(g(t)=5t^5−2t^3+7t\)

\(h(p)=6p−p^3−2\)

Solution

For the function \(f(x)\), the highest power of \(x\) is 3, so the degree is 3. The leading term is the term containing that degree, \(−4x^3\). The leading coefficient is the coefficient of that term, −4.

For the function \(g(t)\), the highest power of \(t\) is 5, so the degree is 5. The leading term is the term containing that degree, \(5t^5\). The leading coefficient is the coefficient of that term, 5.

For the function \(h(p)\), the highest power of \(p\) is 3, so the degree is 3. The leading term is the term containing that degree, \(−p^3\); the leading coefficient is the coefficient of that term, −1.

Exercise \(\PageIndex{3}\)

Identify the degree, leading term, and leading coefficient of the polynomial \(f(x)=4x^2−x^6+2x−6\).

Answer

The degree is \(6.\) The leading term is \(−x^6\). The leading coefficient is \(−1.\)

Key Equations

• general form of a polynomial function: \(f(x)=a_nx^n+a_{n-1}x^{n-1}...+a_2x^2+a_1x+a_0\)

Key Concepts

• A power function is a variable base raised to a number power.
• A polynomial function is the sum of terms, each of which consists of a transformed power function with positive whole number power.
• The degree of a polynomial function is the highest power of the variable that occurs in a polynomial. The term containing the highest power of the variable is called the leading term. The coefficient of the leading term is called the leading coefficient.

Glossary

coefficient

a nonzero real number that is multiplied by a variable raised to an exponent (only the number factor is the coefficient)

degree

the highest power of the variable that occurs in a polynomial

leading coefficient

the coefficient of the leading term

leading term

the term containing the highest power of the variable

polynomial function

a function that consists of either zero or the sum of a finite number of non-zero terms, each of which is a product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.

power function

a function that can be represented in the form \(f(x)=kx^p\) where \(k\) is a constant, the base is a variable, and the exponent, \(p\), is a constant

term of a polynomial function

any \(a_ix^i\) of a polynomial function in the form \(f(x)=a_nx^n+a_{n-1}x^{n-1}...+a_2x^2+a_1x+a_0\)