5.1E: Exercises

Exercises

In Exercises 1 - 12, use the given pair of functions to find the following values if they exist.

• \((g\circ f)(0)\)
• \((f\circ g)(-1)\)
• \((f \circ f)(2)\)
• \((g\circ f)(-3)\)
• \((f\circ g)\left(\dfrac{1}{2}\right)\)
• \((f \circ f)(-2)\)

1. \(f(x) = x^2\), \(g(x) = 2x+1\)
2. \(f(x) = 4-x\), \(g(x) = 1-x^2\)
3. \(f(x) = 4-3x\), \(g(x) = |x|\)
4. \(f(x) = |x-1|\), \(g(x) = x^2-5\)
5. \(f(x) = 4x+5\), \(g(x) = \sqrt{x}\)
6. \(f(x) = \sqrt{3-x}\), \(g(x) = x^2+1\)
7. \(f(x) = 6-x-x^2\), \(g(x) = x\sqrt{x+10}\)
8. \(f(x) = \sqrt[3]{x+1}\), \(g(x) = 4x^2-x\)
9. \(f(x) = \dfrac{3}{1-x}\), \(g(x) = \dfrac{4x}{x^2+1}\)
10. \(f(x) = \dfrac{x}{x+5}\), \(g(x) = \dfrac{2}{7-x^2}\)
11. \(f(x) = \dfrac{2x}{5-x^2}\), \(g(x) = \sqrt{4x+1}\)
12. \(f(x) =\sqrt{2x+5}\), \(g(x) = \dfrac{10x}{x^2+1}\)

In Exercises 13 - 24, use the given pair of functions to find and simplify expressions for the following functions and state the domain of each using interval notation.

• \((g \circ f)(x)\)
• \((f \circ g)(x)\)
• \((f \circ f)(x)\)

13. \(f(x) = 2x+3\), \(g(x) = x^2-9\)
14. \(f(x) = x^2 -x+1\), \(g(x) = 3x-5\)
15. \(f(x) = x^2-4\), \(g(x) = |x|\)
16. \(f(x) = 3x-5\), \(g(x) = \sqrt{x}\)
17. \(f(x) = |x+1|\), \(g(x) = \sqrt{x}\)
18. \(f(x) = 3-x^2\), \(g(x) = \sqrt{x+1}\)
19. \(f(x) = |x|\), \(g(x) = \sqrt{4-x}\)
20. \(f(x) = x^2-x-1\), \(g(x) = \sqrt{x-5}\)
21. \(f(x) = 3x-1\), \(g(x) = \dfrac{1}{x+3}\)
22. \(f(x) = \dfrac{3x}{x-1}\), \(g(x) =\dfrac{x}{x-3}\)
23. \(f(x) = \dfrac{x}{2x+1}\), \(g(x) = \dfrac{2x+1}{x}\)
24. \(f(x) = \dfrac{2x}{x^2-4}\), \(g(x) =\sqrt{1-x}\)

In Exercises 25 - 30, use \(f(x) = -2x\), \(g(x) = \sqrt{x}\) and \(h(x) = |x|\) to find and simplify expressions for the following functions and state the domain of each using interval notation.

25. \((h\circ g \circ f)(x)\)
26. \((h\circ f \circ g)(x)\)
27. \((g\circ f \circ h)(x)\)
28. \((g\circ h \circ f)(x)\)
29. \((f\circ h \circ g)(x)\)
30. \((f\circ g \circ h)(x)\)

In Exercises 31 - 40, write the given function as a composition of two or more non-identity functions. (There are several correct answers, so check your answer using function composition.)

31. \(p(x) = (2x+3)^3\)
32. \(P(x) = \left(x^2-x+1\right)^5\)
33. \(h(x) = \sqrt{2x-1}\)
34. \(H(x) = |7-3x|\)
35. \(r(x) = \dfrac{2}{5x+1}\)
36. \(R(x) = \dfrac{7}{x^2-1}\)
37. \(q(x) = \dfrac{|x|+1}{|x|-1}\)
38. \(Q(x) = \dfrac{2x^3+1}{x^3-1}\)
39. \(v(x) = \dfrac{2x+1}{3-4x}\)
40. \(w(x) = \dfrac{x^2}{x^4+1}\)
41. Write the function \(F(x) = \sqrt{\dfrac{x^{3} + 6}{x^{3} - 9}}\) as a composition of three or more non-identity functions.
42. Let \(g(x) = -x, \, h(x) = x + 2, \, j(x) = 3x\) and \(k(x) = x - 4\). In what order must these functions be composed with \(f(x) = \sqrt{x}\) to create \(F(x) = 3\sqrt{-x + 2} - 4\)?
43. What linear functions could be used to transform \(f(x) = x^{3}\) into \(F(x) = -\dfrac{1}{2}(2x - 7)^{3} + 1\)? What is the proper order of composition?

In Exercises 44 - 55, let \(f\) be the function defined by \[f = \{(-3, 4), (-2, 2), (-1, 0), (0, 1), (1, 3), (2, 4), (3, -1)\}\nonumber\] and let \(g\) be the function defined by\[g = \{(-3, -2), (-2, 0), (-1, -4), (0, 0), (1, -3), (2, 1), (3, 2)\}.\nonumber\]Find the value if it exists.

44. \((f \circ g)(3)\)
45. \(f(g(-1))\)
46. \((f \circ f)(0)\)
47. \((f \circ g)(-3)\)
48. \((g \circ f)(3)\)
49. \(g(f(-3))\)
50. \((g \circ g)(-2)\)
51. \((g \circ f)(-2)\)
52. \(g(f(g(0)))\)
53. \(f(f(f(-1)))\)
54. \(f(f(f(f(f(1)))))\)
55. \(\underbrace{(g \circ g \circ \cdots \circ g)}_{n \text { times }}(0)\)

In Exercises 56 - 61, use the graphs of \(y=f(x)\) and \(y=g(x)\) below to find the function value.

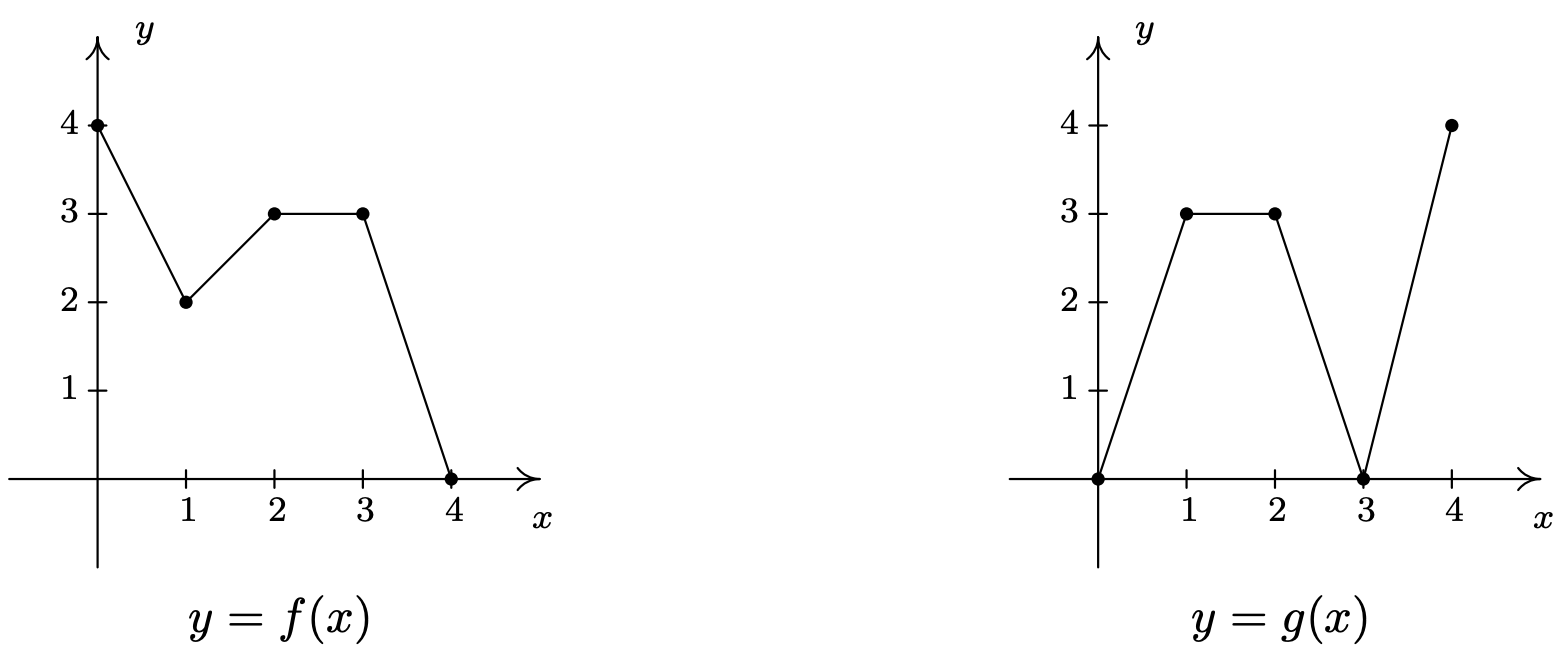
56. \((g\circ f)(1)\)
57. \((f \circ g)(3)\)
58. \((g\circ f)(2)\)
59. \((f\circ g)(0)\)
60. \((f\circ f)(1)\)
61. \((g \circ g)(1)\)
62. The volume \(V\) of a cube is a function of its side length \(x\). Let’s assume that \(x = t + 1\) is also a function of time \(t\), where \(x\) is measured in inches and \(t\) is measured in minutes. Find a formula for \(V\) as a function of \(t\).
63. Suppose a local vendor charges \(\$2\) per hot dog and that the number of hot dogs sold per hour \(x\) is given by \(x(t) = -4t^2+20t+92\), where \(t\) is the number of hours since \(10\) AM, \(0 \leq t \leq 4\).
    1. Find an expression for the revenue per hour \(R\) as a function of \(x\).
    2. Find and simplify \(\left(R \circ x\right)(t)\). What does this represent?
    3. What is the revenue per hour at noon?
64. Discuss with your classmates how ‘real-world’ processes such as filling out federal income tax forms or computing your final course grade could be viewed as a use of function composition. Find a process for which composition with itself (iteration) makes sense.

Answers

1. For \(f(x) = x^2\) and \(g(x) = 2x+1\),
   • \((g\circ f)(0) = 1\)
   • \((f\circ g)(-1) = 1\)
   • \((f \circ f)(2) = 16\)
   • \((g\circ f)(-3) = 19\)
   • \((f\circ g)\left(\dfrac{1}{2}\right) = 4\)
   • \((f \circ f)(-2) = 16\)
2. For \(f(x) = 4-x\) and \(g(x) = 1-x^2\),
   • \((g\circ f)(0) = -15\)
   • \((f\circ g)(-1) = 4\)
   • \((f \circ f)(2) = 2\)
   • \((g\circ f)(-3) = -48\)
   • \((f\circ g)\left(\dfrac{1}{2}\right) = \dfrac{13}{4}\)
   • \((f \circ f)(-2) = -2\)
3. For \(f(x) = 4-3x\) and \(g(x) = |x|\),
   • \((g\circ f)(0) = 4\)
   • \((f\circ g)(-1) = 1\)
   • \((f \circ f)(2) = 10\)
   • \((g\circ f)(-3) = 13\)
   • \((f\circ g)\left(\dfrac{1}{2}\right) = \dfrac{5}{2}\)
   • \((f \circ f)(-2) = -26\)
4. For \(f(x) = |x-1|\) and \(g(x) = x^2-5\),
   • \((g\circ f)(0) = -4\)
   • \((f\circ g)(-1) = 5\)
   • \((f \circ f)(2) = 0\)
   • \((g\circ f)(-3) = 11\)
   • \((f\circ g)\left(\dfrac{1}{2}\right) = \dfrac{23}{4}\)
   • \((f \circ f)(-2) = 2\)
5. For \(f(x) = 4x+5\) and \(g(x) = \sqrt{x}\),
   • \((g\circ f)(0) = \sqrt{5}\)
   • \((f\circ g)(-1)\) is not real
   • \((f \circ f)(2) = 57\)
   • \((g\circ f)(-3)\) is not real
   • \((f\circ g)\left(\dfrac{1}{2}\right) = 5+2\sqrt{2}\)
   • \((f \circ f)(-2) = -7\)
6. For \(f(x) = \sqrt{3-x}\) and \(g(x) = x^2+1\),
   • \((g\circ f)(0) = 4\)
   • \((f\circ g)(-1) = 1\)
   • \((f \circ f)(2) = \sqrt{2}\)
   • \((g\circ f)(-3) = 7\)
   • \((f\circ g)\left(\dfrac{1}{2}\right) = \dfrac{\sqrt{7}}{2}\)
   • \((f \circ f)(-2) = \sqrt{3 - \sqrt{5}}\)
7. For \(f(x) = 6-x-x^2\) and \(g(x) = x\sqrt{x+10}\),
   • \((g\circ f)(0) = 24\)
   • \((f\circ g)(-1) = 0\)
   • \((f \circ f)(2) = 6\)
   • \((g\circ f)(-3) = 0\)
   • \((f\circ g)\left(\dfrac{1}{2}\right) = \dfrac{27-2\sqrt{42}}{8}\)
   • \((f \circ f)(-2) = -14\)
8. For \(f(x) = \sqrt[3]{x+1}\) and \(g(x) = 4x^2-x\),
   • \((g\circ f)(0) = 3\)
   • \((f\circ g)(-1) = \sqrt[3]{6}\)
   • \((f \circ f)(2) = \sqrt[3]{\sqrt[3]{3}+1}\)
   • \((g\circ f)(-3) = 4\sqrt[3]{4}+\sqrt[3]{2}\)
   • \((f\circ g)\left(\dfrac{1}{2}\right) = \dfrac{\sqrt[3]{12}}{2}\)
   • \((f \circ f)(-2) = 0\)
9. For \(f(x) = \dfrac{3}{1-x}\) and \(g(x) = \dfrac{4x}{x^2+1}\),
   • \((g\circ f)(0) = \dfrac{6}{5}\)
   • \((f\circ g)(-1) = 1\)
   • \((f \circ f)(2) = \dfrac{3}{4}\)
   • \((g\circ f)(-3) = \dfrac{48}{25}\)
   • \((f\circ g)\left(\dfrac{1}{2}\right) = -5\)
   • \((f \circ f)(-2)\) is undefined
10. For \(f(x) = \dfrac{x}{x+5}\) and \(g(x) = \dfrac{2}{7-x^2}\),
    • \((g\circ f)(0) = \dfrac{2}{7}\)
    • \((f\circ g)(-1) = \dfrac{1}{16}\)
    • \((f \circ f)(2) = \dfrac{2}{37}\)
    • \((g\circ f)(-3) = \dfrac{8}{19}\)
    • \((f\circ g)\left(\dfrac{1}{2}\right) = \dfrac{8}{143}\)
    • \((f \circ f)(-2) = -\dfrac{2}{13}\)
11. For \(f(x) = \dfrac{2x}{5-x^2}\) and \(g(x) = \sqrt{4x+1}\),
    • \((g\circ f)(0) = 1\)
    • \((f\circ g)(-1)\) is not real
    • \((f \circ f)(2) = -\dfrac{8}{11}\)
    • \((g\circ f)(-3) = \sqrt{7}\)
    • \((f\circ g)\left(\dfrac{1}{2}\right) = \sqrt{3}\)
    • \((f \circ f)(-2) = \dfrac{8}{11}\)
12. For \(f(x) =\sqrt{2x+5}\) and \(g(x) = \dfrac{10x}{x^2+1}\),
    • \((g\circ f)(0) = \dfrac{5\sqrt{5}}{3}\)
    • \((f\circ g)(-1)\) is not real
    • \((f \circ f)(2) = \sqrt{11}\)
    • \((g\circ f)(-3)\) is not real
    • \((f\circ g)\left(\dfrac{1}{2}\right) = \sqrt{13}\)
    • \((f \circ f)(-2) = \sqrt{7}\)
13. For \(f(x) = 2x+3\) and \(g(x) = x^2-9\)
    • \((g \circ f)(x) = 4x^2+12x\), domain: \((-\infty, \infty)\)
    • \((f \circ g)(x) = 2x^2-15\), domain: \((-\infty, \infty)\)
    • \((f \circ f)(x) = 4x+9\), domain: \((-\infty, \infty)\)
14. For \(f(x) = x^2 -x+1\) and \(g(x) = 3x-5\)
    • \((g \circ f)(x) = 3x^2-3x-2\), domain: \((-\infty, \infty)\)
    • \((f \circ g)(x) =9x^2-33x+31\), domain: \((-\infty, \infty)\)
    • \((f \circ f)(x) = x^4-2x^3+2x^2-x+1\), domain: \((-\infty, \infty)\)
15. For \(f(x) = x^2-4\) and \(g(x) = |x|\)
    • \((g \circ f)(x) = |x^2-4|\), domain: \((-\infty, \infty)\)
    • \((f \circ g)(x) =|x|^2-4 = x^2-4\), domain: \((-\infty, \infty)\)
    • \((f \circ f)(x) =x^4-8x^2+12\), domain: \((-\infty, \infty)\)
16. For \(f(x) = 3x-5\) and \(g(x) = \sqrt{x}\)
    • \((g \circ f)(x) = \sqrt{3x-5}\), domain: \(\left[ \dfrac{5}{3}, \infty \right)\)
    • \((f \circ g)(x) = 3\sqrt{x}-5\), domain: \([0,\infty)\)
    • \((f \circ f)(x) = 9x-20\), domain: \((-\infty, \infty)\)
17. For \(f(x) = |x+1|\) and \(g(x) = \sqrt{x}\)
    • \((g \circ f)(x) = \sqrt{|x+1|}\), domain: \((-\infty, \infty)\)
    • \((f \circ g)(x) = |\sqrt{x}+1| = \sqrt{x}+1\), domain: \([0,\infty)\)
    • \((f \circ f)(x) = ||x+1|+1| = |x+1|+1\), domain: \((-\infty, \infty)\)
18. For \(f(x) = 3-x^2\) and \(g(x) = \sqrt{x+1}\)
    • \((g \circ f)(x) = \sqrt{4-x^2}\), domain: \([-2,2]\)
    • \((f \circ g)(x) =2-x\), domain: \([-1, \infty)\)
    • \((f \circ f)(x) = -x^4+6x^2-6\), domain: \((-\infty, \infty)\)
19. For \(f(x) = |x|\) and \(g(x) = \sqrt{4-x}\)
    • \((g \circ f)(x) = \sqrt{4-|x|}\), domain: \([-4,4]\)
    • \((f \circ g)(x) =|\sqrt{4-x}| = \sqrt{4-x}\), domain: \((-\infty, 4]\)
    • \((f \circ f)(x) = | |x| | = |x|\), domain: \((-\infty, \infty)\)
20. For \(f(x) = x^2-x-1\) and \(g(x) = \sqrt{x-5}\)
    • \((g \circ f)(x) = \sqrt{x^2-x-6}\), domain: \((-\infty, -2] \cup [3,\infty)\)
    • \((f \circ g)(x) =x-6-\sqrt{x-5}\), domain: \([5,\infty)\)
    • \((f \circ f)(x) =x^4-2x^3-2x^2+3x+1\), domain: \((-\infty, \infty)\)
21. For \(f(x) = 3x-1\) and \(g(x) = \dfrac{1}{x+3}\)
    • \((g \circ f)(x) = \dfrac{1}{3x+2}\), domain: \(\left(-\infty, -\dfrac{2}{3}\right) \cup \left(-\dfrac{2}{3}, \infty\right)\)
    • \((f \circ g)(x) = -\dfrac{x}{x+3}\), domain: \(\left(-\infty, -3\right) \cup \left(-3, \infty\right)\)
    • \((f \circ f)(x) = 9x-4\), domain: \((-\infty, \infty)\)
22. For \(f(x) = \dfrac{3x}{x-1}\) and \(g(x) =\dfrac{x}{x-3}\)
    • \((g \circ f)(x) =x\), domain: \(\left(-\infty, 1\right) \cup (1, \infty)\)
    • \((f \circ g)(x) =x\), domain: \(\left(-\infty, 3\right) \cup (3,\infty)\)
    • \((f \circ f)(x) = \dfrac{9x}{2x+1}\), domain: \(\left(-\infty, -\dfrac{1}{2}\right) \cup \left(-\dfrac{1}{2}, 1 \right) \cup \left(1,\infty \right)\)
23. For \(f(x) = \dfrac{x}{2x+1}\) and \(g(x) = \dfrac{2x+1}{x}\)
    • \((g \circ f)(x) = \dfrac{4x+1}{x}\), domain: \(\left(-\infty, -\dfrac{1}{2}\right) \cup \left(-\dfrac{1}{2}, 0), \cup (0, \infty\right)\)
    • \((f \circ g)(x) = \dfrac{2x+1}{5x+2}\), domain: \(\left(-\infty, -\dfrac{2}{5}\right) \cup \left(-\dfrac{2}{5}, 0\right) \cup (0,\infty)\)
    • \((f \circ f)(x) = \dfrac{x}{4x+1}\), domain: \(\left(-\infty, -\dfrac{1}{2}\right) \cup \left(-\dfrac{1}{2}, -\dfrac{1}{4} \right) \cup \left(-\dfrac{1}{4},\infty\right)\)
24. For \(f(x) = \dfrac{2x}{x^2-4}\) and \(g(x) =\sqrt{1-x}\)
    • \((g \circ f)(x) =\sqrt{\dfrac{x^2-2x-4}{x^2-4}}\), domain: \(\left(-\infty, -2\right) \cup \left[1-\sqrt{5}, 2\right) \cup \left[1+\sqrt{5}, \infty\right)\)
    • \((f \circ g)(x) = -\dfrac{2\sqrt{1-x}}{x+3}\), domain: \(\left(-\infty, -3\right) \cup \left(-3, 1\right]\)
    • \((f \circ f)(x) = \dfrac{4x-x^3}{x^4-9x^2+16}\), domain: \(\left(-\infty, -\dfrac{1+\sqrt{17}}{2}\right) \cup \left(-\dfrac{1+\sqrt{17}}{2}, -2\right) \cup \left(-2, \dfrac{1-\sqrt{17}}{2}\right) \cup \left(\dfrac{1-\sqrt{17}}{2}, \dfrac{-1+\sqrt{17}}{2}\right) \cup \left(\dfrac{-1+\sqrt{17}}{2}, 2\right) \cup \left(2, \dfrac{1+\sqrt{17}}{2} \right) \cup \left(\dfrac{1+\sqrt{17}}{2}, \infty\right)\)
25. \((h\circ g \circ f)(x)= |\sqrt{-2x}|= \sqrt{-2x}\), domain: \((-\infty, 0]\)
26. \((h\circ f \circ g)(x) = |-2\sqrt{x}|= 2\sqrt{x}\), domain: \([0,\infty)\)
27. \((g\circ f \circ h)(x) = \sqrt{-2|x|}\), domain: \(\{0\}\)
28. \((g\circ h \circ f)(x) = \sqrt{|-2x|} = \sqrt{2|x|}\), domain: \((-\infty, \infty)\)
29. \((f\circ h \circ g)(x) = -2|\sqrt{x}| = -2\sqrt{x}\), domain: \([0,\infty)\)
30. \((f\circ g \circ h)(x) = -2\sqrt{|x|}\), , domain: \((-\infty,\infty)\)
31. Let \(f(x) = 2x+3\) and \(g(x) = x^3\), then \(p(x) = (g\circ f)(x)\).
32. Let \(f(x) = x^2-x+1\) and \(g(x) = x^5\), \(P(x) =(g\circ f)(x)\).
33. Let \(f(x) = 2x-1\) and \(g(x) = \sqrt{x}\), then \(h(x) = (g\circ f)(x)\).
34. Let \(f(x) = 7-3x\) and \(g(x) = |x|\), then \(H(x) = (g\circ f)(x)\).
35. Let \(f(x) = 5x+1\) and \(g(x) = \dfrac{2}{x}\), then \(r(x) =(g\circ f)(x)\).
36. Let \(f(x) = x^2-1\) and \(g(x) = \dfrac{7}{x}\), then \(R(x) =(g\circ f)(x)\).
37. Let \(f(x) = |x|\) and \(g(x) = \dfrac{x+1}{x-1}\), then \(q(x) =(g\circ f)(x)\).
38. Let \(f(x) = x^3\) and \(g(x)= \dfrac{2x+1}{x-1}\), then \(Q(x) =(g\circ f)(x)\).
39. Let \(f(x) =2x\) and \(g(x) = \dfrac{x+1}{3-2x}\), then \(v(x) =(g\circ f)(x)\).
40. Let \(f(x) = x^2\) and \(g(x) = \dfrac{x}{x^2+1}\), then \(w(x) =(g\circ f)(x)\).
41. \(F(x) = \sqrt{\dfrac{x^{3} + 6}{x^{3} - 9}} = (h(g(f(x)))\) where \(f(x) = x^{3}, \, g(x) = \dfrac{x + 6}{x - 9}\) and \(h(x) = \sqrt{x}\).
42. \(F(x) = 3\sqrt{-x + 2} - 4 = k(j(f(h(g(x)))))\)
43. One possible solution is \(F(x) = -\dfrac{1}{2}(2x - 7)^{3} + 1 = k(j(f(h(g(x)))))\) where \(g(x) = 2x, \, h(x) = x - 7, \, j(x) = -\dfrac{1}{2}x\) and \(k(x) = x + 1\). You could also have \(F(x) = H(f(G(x)))\) where \(G(x) = 2x - 7\) and \(H(x) = -\dfrac{1}{2}x + 1\).
44. \((f \circ g)(3)= f(g(3)) = f(2) = 4\)
45. \(f(g(-1)) = f(-4)\) which is undefined
46. \((f \circ f)(0) = f(f(0)) = f(1) = 3\)
47. \((f \circ g)(-3) = f(g(-3)) = f(-2) = 2\)
48. \((g \circ f)(3) = g(f(3)) = g(-1) = -4\)
49. \(g(f(-3)) = g(4)\) which is undefined
50. \((g \circ g)(-2) = g(g(-2)) = g(0) = 0\)
51. \((g \circ f)(-2) = g(f(-2)) = g(2) = 1\)
52. \(g(f(g(0))) = g(f(0)) = g(1) = -3\)
53. \(f(f(f(-1))) = f(f(0)) = f(1) = 3\)
54. \(f(f(f(f(f(1))))) = f(f(f(f(3)))) =\\ f(f(f(-1))) = f(f(0)) = f(1) = 3\)
55. \(\underbrace{(g \circ g \circ \cdots \circ g)}_{n \text { times }}(0)=0\)
56. \((g\circ f)(1) = 3\)
57. \((f \circ g)(3) = 4\)
58. \((g\circ f)(2) = 0\)
59. \((f\circ g)(0) = 4\)
60. \((f\circ f)(1) = 3\)
61. \((g \circ g)(1) = 0\)
62. \(V(x) = x^{3}\) so \(V(x(t)) = (t + 1)^{3}\)
63. 1. \(R(x) = 2x\)
    2. \(\left(R \circ x \right)(t) = -8t^2+40t+184\), \(0 \leq t \leq 4\). This gives the revenue per hour as a function of time.
    3. Noon corresponds to \(t=2\), so \(\left(R \circ x \right)(2) = 232\). The hourly revenue at noon is \(\$232\) per hour.