6.1E: Exercises

Exercises

In Exercises 1 - 15, use the property: \(b^{a}=c\) if and only if \(\log _{b}(c)=a\) from Theorem 6.1.2 to rewrite the given equation in the other form. That is, rewrite the exponential equations as logarithmic equations and rewrite the logarithmic equations as exponential equations.

1. \(2^{3}=8\)
2. \(5^{-3}=\frac{1}{125}\)
3. \(4^{5 / 2}=32\)
4. \(\left(\frac{1}{3}\right)^{-2}=9\)
5. \(\left(\frac{4}{25}\right)^{-1 / 2}=\frac{5}{2}\)
6. \(10^{-3}=0.001\)
7. \(e^{0}=1\)
8. \(\log _{5}(25)=2\)
9. \(\log _{25}(5)=\frac{1}{2}\)
10. \(\log _{3}\left(\frac{1}{81}\right)=-4\)
11. \(\log _{\frac{4}{3}}\left(\frac{3}{4}\right)=-1\)
12. \(\log (100)=2\)
13. \(\log (0.1)=-1\)
14. \(\ln (e)=1\)
15. \(\ln \left(\frac{1}{\sqrt{e}}\right)=-\frac{1}{2}\)

In Exercises 16 - 42, evaluate the expression.

16. \(\log _{3}(27)\)
17. \(\log _{6}(216)\)
18. \(\log _{2}(32)\)
19. \(\log _{6}\left(\frac{1}{36}\right)\)
20. \(\log _{8}(4)\)
21. \(\log _{36}(216)\)
22. \(\log _{\frac{1}{5}}(625)\)
23. \(\log _{\frac{1}{6}}(216)\)
24. \(\log _{36}(36)\)
25. \(\log \left(\frac{1}{1000000}\right)\)
26. \(\log (0.01)\)
27. \(\ln \left(e^{3}\right)\)
28. \(\log _{4}(8)\)
29. \(\log _{6}(1)\)
30. \(\log _{13}(\sqrt{13})\)
31. \(\log _{36}(\sqrt[4]{36})\)
32. \(7^{\log _{7}(3)}\)
33. \(36^{\log _{36}(216)}\)
34. \(\log _{36}\left(36^{216}\right)\)
35. \(\ln \left(e^{5}\right)\)
36. \(\log \left(\sqrt[9]{10^{11}}\right)\)
37. \(\log \left(\sqrt[3]{10^{5}}\right)\)
38. \(\ln \left(\frac{1}{\sqrt{e}}\right)\)
39. \(\log _{5}\left(3^{\log _{3}(5)}\right)\)
40. \(\log \left(e^{\ln (100)}\right)\)
41. \(\log _{2}\left(3^{-\log _{3}(2)}\right)\)
42. \(\ln \left(42^{6 \log (1)}\right)\)

In Exercises 43 - 57, find the domain of the function.

43. \(f(x)=\ln \left(x^{2}+1\right)\)
44. \(f(x)=\log _{7}(4 x+8)\)
45. \(f(x)=\ln (4 x-20)\)
46. \(f(x)=\log \left(x^{2}+9 x+18\right)\)
47. \(f(x)=\log \left(\frac{x+2}{x^{2}-1}\right)\)
48. \(f(x)=\log \left(\frac{x^{2}+9 x+18}{4 x-20}\right)\)
49. \(f(x)=\ln (7-x)+\ln (x-4)\)
50. \(f(x)=\ln (4 x-20)+\ln \left(x^{2}+9 x+18\right)\)
51. \(f(x)=\log \left(x^{2}+x+1\right)\)
52. \(f(x)=\sqrt[4]{\log _{4}(x)}\)
53. \(f(x)=\log _{9}(|x+3|-4)\)
54. \(f(x)=\ln (\sqrt{x-4}-3)\)
55. \(f(x)=\frac{1}{3-\log _{5}(x)}\)
56. \(f(x)=\frac{\sqrt{-1-x}}{\log _{\frac{1}{2}}(x)}\)
57. \(f(x)=\ln \left(-2 x^{3}-x^{2}+13 x-6\right)\)

In Exercises 58 - 63, sketch the graph of \(y = g(x)\) by starting with the graph of \(y = f(x)\) and using transformations. Track at least three points of your choice and the horizontal asymptote through the transformations. State the domain and range of \(g\).

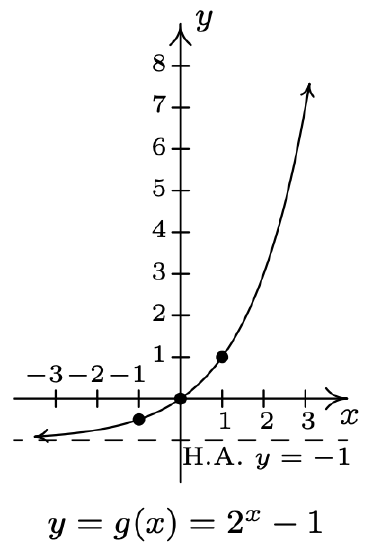
58. \(f(x)=2^{x}, g(x)=2^{x}-1\)
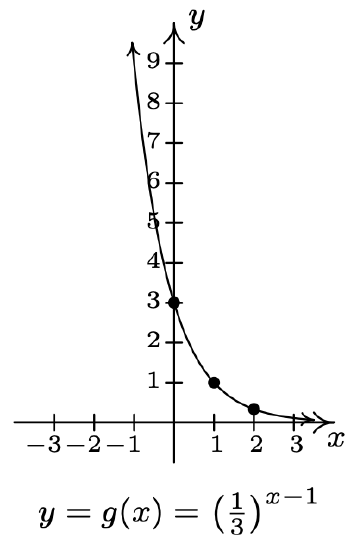
59. \(f(x)=\left(\frac{1}{3}\right)^{x}, g(x)=\left(\frac{1}{3}\right)^{x-1}\)
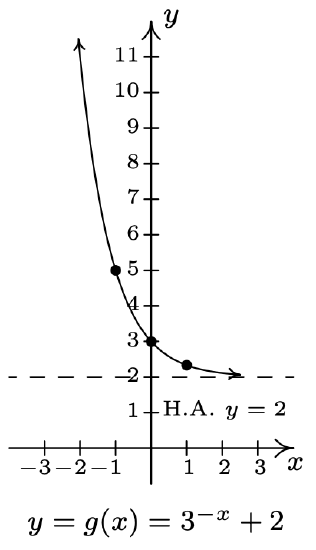
60. \(f(x)=3^{x}, g(x)=3^{-x}+2\)
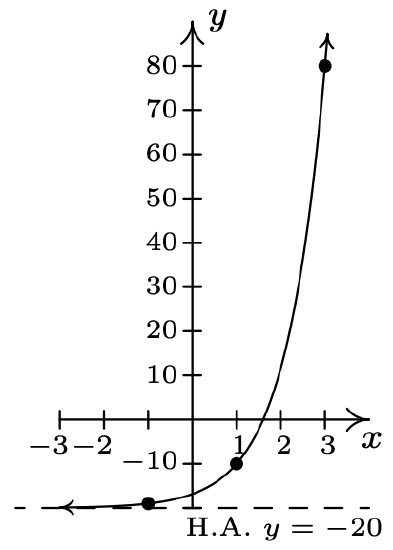
61. \(f(x)=10^{x}, g(x)=10^{\frac{x+1}{2}}-20\)
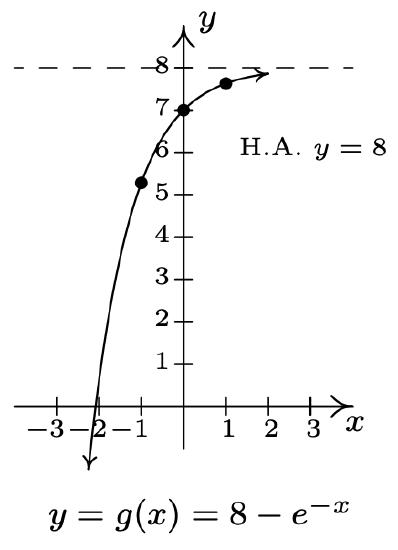
62. \(f(x)=e^{x}, g(x)=8-e^{-x}\)
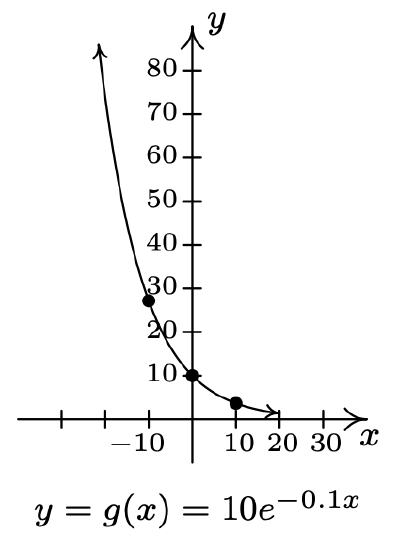
63. \(f(x)=e^{x}, g(x)=10 e^{-0.1 x}\)

In Exercises 64 - 69, sketch the graph of \(y = g(x)\) by starting with the graph of \(y = f(x)\) and using transformations. Track at least three points of your choice and the vertical asymptote through the transformations. State the domain and range of \(g\).

64. \(f(x)=\log _{2}(x), g(x)=\log _{2}(x+1)\)
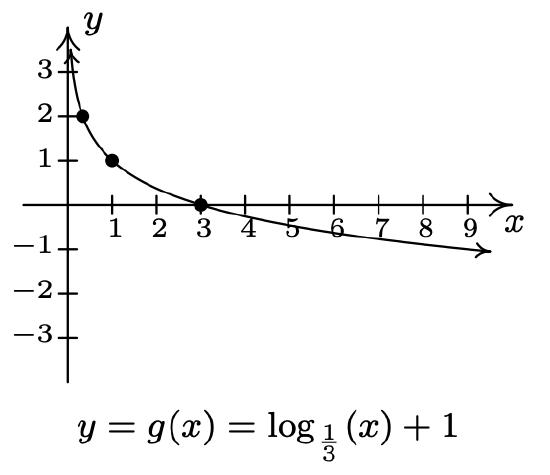
65. \(f(x)=\log _{\frac{1}{3}}(x), g(x)=\log _{\frac{1}{3}}(x)+1\)
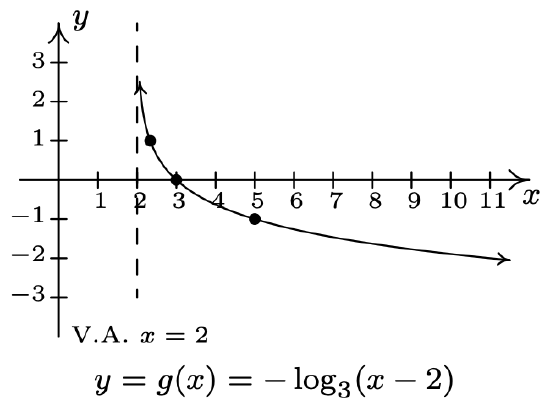
66. \(f(x)=\log _{3}(x), g(x)=-\log _{3}(x-2)\)
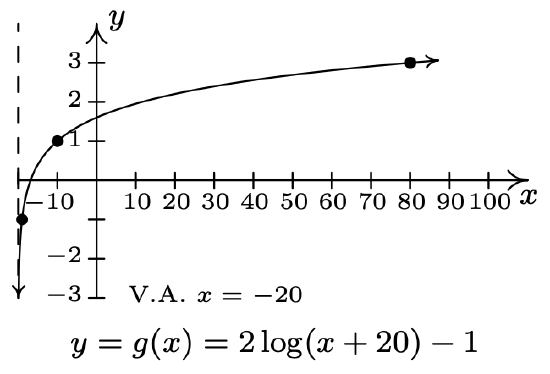
67. \(f(x)=\log (x), g(x)=2 \log (x+20)-1\)
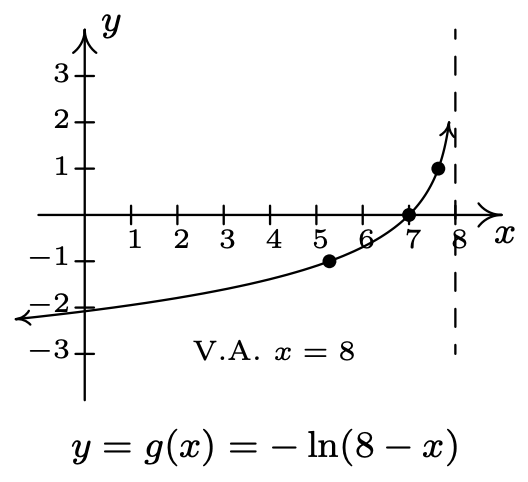
68. \(f(x)=\ln (x), g(x)=-\ln (8-x)\)
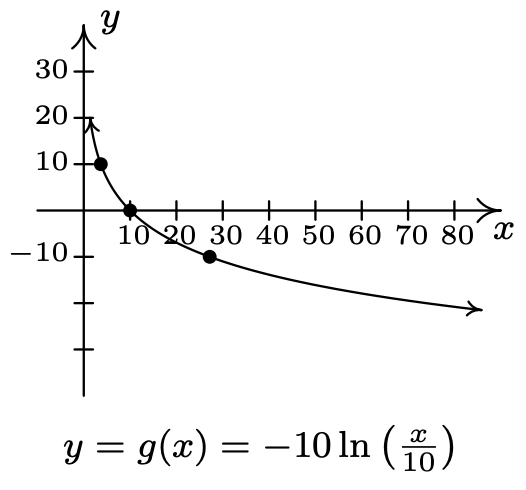
69. \(f(x)=\ln (x), g(x)=-10 \ln \left(\frac{x}{10}\right)\)
70. Verify that each function in Exercises 64 - 69 is the inverse of the corresponding function in Exercises 58 - 63. (Match up #58 and #64, and so on.)

In Exercises 71 - 74, find the inverse of the function from the "procedural perspective" discussed in Example 6.1.5 and graph the function and its inverse on the same set of axes.

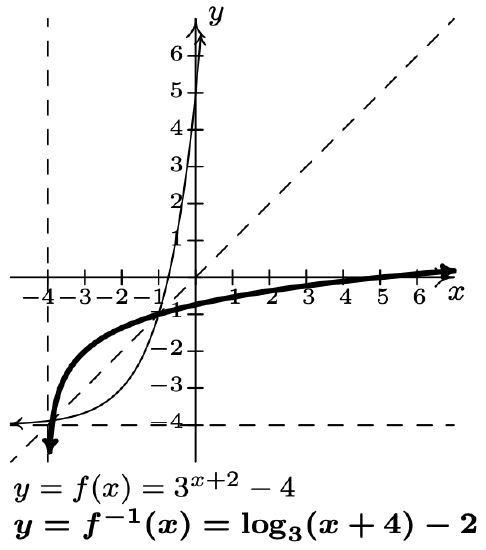
71. \(f(x)=3^{x+2}-4\)
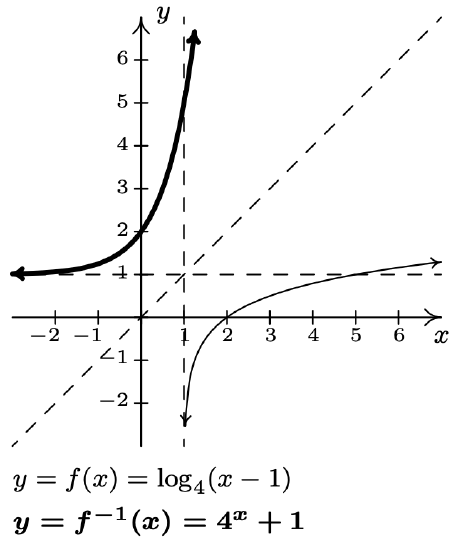
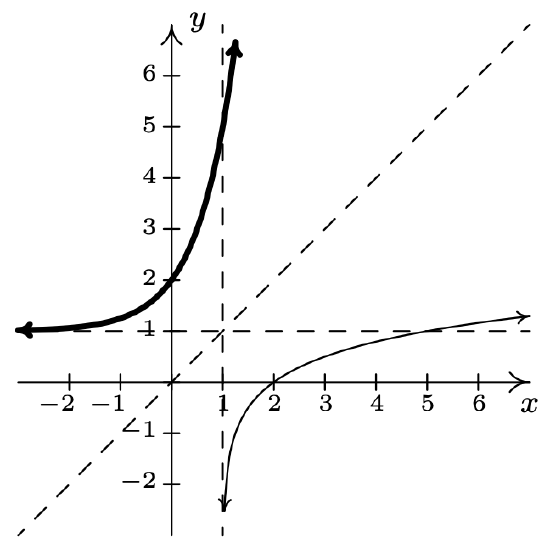
72. \(f(x)=\log _{4}(x-1)\)
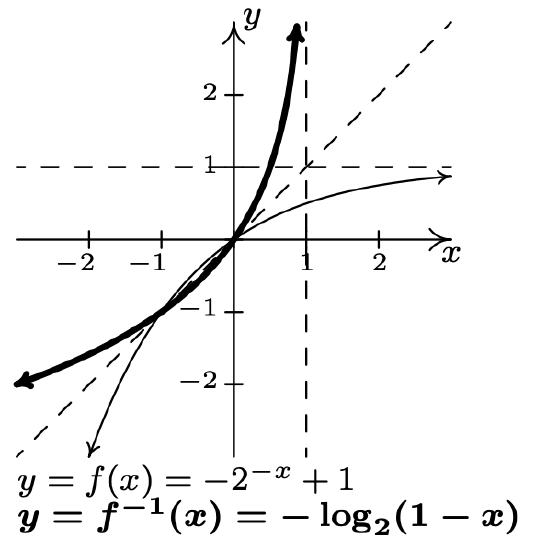
73. \(f(x)=-2^{-x}+1\)
74. \(f(x)=5 \log (x)-2\)

(Logarithmic Scales) In Exercises 75 - 77, we introduce three widely used measurement scales which involve common logarithms: the Richter scale, the decibel scale and the pH scale. The computations involved in all three scales are nearly identical so pay attention to the subtle differences.

75. Earthquakes are complicated events and it is not our intent to provide a complete discussion of the science involved in them. Instead, we refer the interested reader to a solid course in Geology or the U.S. Geological Survey’s Earthquake Hazards Program found here and present only a simplified version of the Richter scale. The Richter scale measures the magnitude of an earthquake by comparing the amplitude of the seismic waves of the given earthquake to those of a “magnitude 0 event”, which was chosen to be a seismograph reading of 0.001 millimeters recorded on a seismometer 100 kilometers from the earthquake’s epicenter. Specifically, the magnitude of an earthquake is given by

    \(M(x)=\log \left(\frac{x}{0.001}\right)\)

    where \(x\) is the seismograph reading in millimeters of the earthquake recorded 100 kilometers from the epicenter.

    1. Show that \(M(0.001) = 0\).
    2. Compute \(M(80, 000)\).
    3. Show that an earthquake which registered 6.7 on the Richter scale had a seismograph reading ten times larger than one which measured 5.7.
    4. Find two news stories about recent earthquakes which give their magnitudes on the Richter scale. How many times larger was the seismograph reading of the earthquake with larger magnitude?
76. While the decibel scale can be used in many disciplines, we shall restrict our attention to its use in acoustics, specifically its use in measuring the intensity level of sound.¹⁴ The Sound Intensity Level \(L\) (measured in decibels) of a sound intensity \(I\) (measured in watts per square meter) is given by

    \(L(I)=10 \log \left(\frac{I}{10^{-12}}\right).\)

    Like the Richter scale, this scale compares \(I\) to baseline: \(10^{-12} \frac{W}{m^{2}}\) is the threshold of human hearing.

    1. Compute \(L\left(10^{-6}\right)\).
    2. Damage to your hearing can start with short term exposure to sound levels around 115 decibels. What intensity \(I\) is needed to produce this level?
    3. Compute \(L(1)\). How does this compare with the threshold of pain which is around 140 decibels?
77. The pH of a solution is a measure of its acidity or alkalinity. Specifically, \(\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]\) where \(\left[\mathrm{H}^{+}\right]\) is the hydrogen ion concentration in moles per liter. A solution with a pH less than 7 is an acid, one with a pH greater than 7 is a base (alkaline) and a pH of 7 is regarded as neutral.
    1. The hydrogen ion concentration of pure water is \(\left[\mathrm{H}^{+}\right]=10^{-7}\). Find its pH.
    2. Find the pH of a solution with \(\left[\mathrm{H}^{+}\right]=6.3 \times 10^{-13}\).
    3. The pH of gastric acid (the acid in your stomach) is about 0.7. What is the corresponding hydrogen ion concentration?
78. Show that \(\log _{b} 1=0\) and \(\log _{b} b=1\) for every \(b>0, b \neq 1\).
79. (Crazy bonus question) Without using your calculator, determine which is larger: \(e^{\pi}\) or \(\pi^{e}\).

Answers

1. \(\log _{2}(8)=3\)
2. \(\log _{5}\left(\frac{1}{125}\right)=-3\)
3. \(\log _{4}(32)=\frac{5}{2}\)
4. \(\log _{\frac{1}{3}}(9)=-2\)
5. \(\log _{\frac{4}{25}}\left(\frac{5}{2}\right)=-\frac{1}{2}\)
6. \(\log (0.001)=-3\)
7. \(\ln (1)=0\)
8. \(5^{2}=25\)
9. \((25)^{\frac{1}{2}}=5\)
10. \(3^{-4}=\frac{1}{81}\)
11. \(\left(\frac{4}{3}\right)^{-1}=\frac{3}{4}\)
12. \(10^{2}=100\)
13. \(10^{-1}=0.1\)
14. \(e^{1}=e\)
15. \(e^{-\frac{1}{2}}=\frac{1}{\sqrt{e}}\)
16. \(\log _{3}(27)=3\)
17. \(\log _{6}(216)=3\)
18. \(\log _{2}(32)=5\)
19. \(\log _{6}\left(\frac{1}{36}\right)=-2\)
20. \(\log _{8}(4)=\frac{2}{3}\)
21. \(\log _{36}(216)=\frac{3}{2}\)
22. \(\log _{\frac{1}{5}}(625)=-4\)
23. \(\log _{\frac{1}{6}}(216)=-3\)
24. \(\log _{36}(36)=1\)
25. \(\log \frac{1}{1000000}=-6\)
26. \(\log (0.01)=-2\)
27. \(\ln \left(e^{3}\right)=3\)
28. \(\log _{4}(8)=\frac{3}{2}\)
29. \(\log _{6}(1)=0\)
30. \(\log _{13}(\sqrt{13})=\frac{1}{2}\)
31. \(\log _{36}(\sqrt[4]{36})=\frac{1}{4}\)
32. \(7^{\log _{7}(3)}=3\)
33. \(36^{\log _{36}(216)}=216\)
34. \(\log _{36}\left(36^{216}\right)=216\)
35. \(\ln \left(e^{5}\right)=5\)
36. \(\log \left(\sqrt[9]{10^{11}}\right)=\frac{11}{9}\)
37. \(\log \left(\sqrt[3]{10^{5}}\right)=\frac{5}{3}\)
38. \(\ln \left(\frac{1}{\sqrt{e}}\right)=-\frac{1}{2}\)
39. \(\log _{5}\left(3^{\log _{3} 5}\right)=1\)
40. \(\log \left(e^{\ln (100)}\right)=2\)
41. \(\log _{2}\left(3^{-\log _{3}(2)}\right)=-1\)
42. \(\ln \left(42^{6 \log (1)}\right)=0\)
43. \((-\infty, \infty)\)
44. \((-2, \infty)\)
45. \((5, \infty)\)
46. \((-\infty,-6) \cup(-3, \infty)\)
47. \((-2,-1) \cup(1, \infty)\)
48. \((-6,-3) \cup(5, \infty)\)
49. \((4,7)\)
50. \((5, \infty)\)
51. \((-\infty, \infty)\)
52. \([1, \infty)\)
53. \((-\infty,-7) \cup(1, \infty)\)
54. \((13, \infty)\)
55. \((0,125) \cup(125, \infty)\)
56. No domain
57. \((-\infty,-3) \cup\left(\frac{1}{2}, 2\right)\)
58. Domain of \(g\): \((-\infty, \infty)\)

    Range of \(g\): \((-1, \infty)\)

    

59. Domain of \(g\): \((-\infty, \infty)\)

    Range of g: \((0, \infty)\)

    

60. Domain of \(g\): \((-\infty, \infty)\)

    Range of \(g\): \((-20, \infty)\)

    

61. Domain of \(g\): \((-\infty, \infty)\)

    Range of \(g\): \((-\infty, 8)\)

    

62. Domain of \(g\): \((-\infty, \infty)\)

    Range of \(g\): \((0, \infty)\)

    

63. Domain of \(g\): \((-1, \infty)\)

    Range of \(g\): \((-\infty, \infty)\)

    

64. Domain of \(g\): \((-1, \infty)\)

    Range of \(g\): \((-\infty, \infty)\)

    

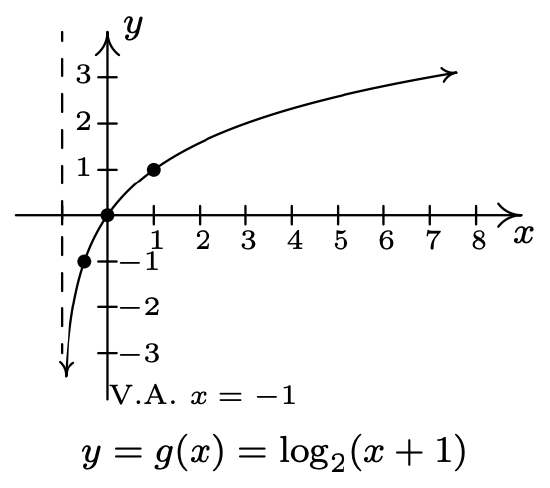
65. Domain of \(g\): \((0, \infty)\)

    Range of \(g\): \((-\infty, \infty)\)

    

66. Domain of \(g\): \((2, \infty)\)

    Range of \(g\): \((-\infty, \infty)\)

    

67. Domain of \(g\): \((-20, \infty)\)

    Range of \(g\): \((-\infty, \infty)\)

    

68. Domain of \(g\): \((-\infty, 8)\)

    Range of \(g\): \((-\infty, \infty)\)

    

69. Domain of \(g\): \((0, \infty)\)

    Range of \(g\): \((-\infty, \infty)\)

    

70. \(f(x)=3^{x+2}-4\)

    \(f^{-1}(x)=\log _{3}(x+4)-2\)

    

71. \(f(x)=\log _{4}(x-1)\)

    \(f^{-1}(x)=4^{x}+1\)

    

72. \(f(x)=\log _{4}(x-1)\)

    \(f^{-1}(x)=4^{x}+1\)

    

73. \(f(x)=-2^{-x}+1\)

    \(f^{-1}(x)=-\log _{2}(1-x)\)

    

74. \(f(x)=5 \log (x)-2\)

    \(f^{-1}(x)=10^{\frac{x+2}{5}}\)

    

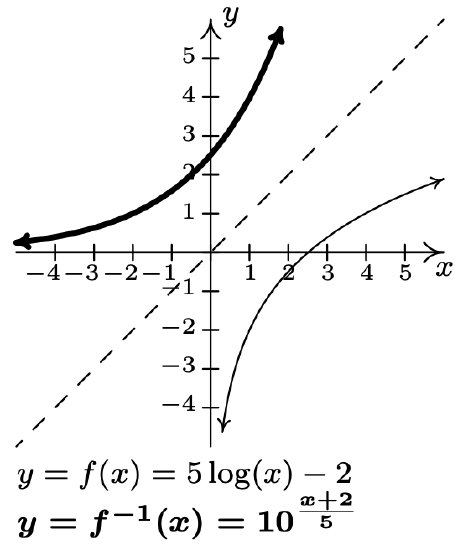
75. 1. \(M(0.001)=\log \left(\frac{0.001}{0.001}\right)=\log (1)=0.\)
    2. \(M(80,000)=\log \left(\frac{80,000}{0.001}\right)=\log (80,000,000) \approx 7.9\)
76. 1. \(L\left(10^{-6}\right)=60\) decibels.
    2. \(I=10^{-.5} \approx 0.316\) watts per square meter.
    3. Since \( L(1)=120\) decibels and \( L(100)=140\) decibels, a sound with intensity level 140 decibels has an intensity 100 times greater than a sound with intensity level 120 decibels.
77. 1. The pH of pure water is 7.
    2. If \(\left[\mathrm{H}^{+}\right]=6.3 \times 10^{-13}\) then the solution has a pH of 12.2.
    3. \(\left[\mathrm{H}^{+}\right]=10^{-0.7} \approx .1995\) moles per liter.