8.5E: Exercises
- Page ID
- 120501
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Exercises
In Exercises 1 - 8, graph the hyperbola. Find the center, the lines which contain the transverse and conjugate axes, the vertices, the foci and the equations of the asymptotes.
- \(\dfrac{x^{2}}{16} - \dfrac{y^{2}}{9} = 1\)
- \(\dfrac{y^{2}}{9} - \dfrac{x^{2}}{16} = 1\)
- \(\dfrac{(x - 2)^{2}}{4} - \dfrac{(y + 3)^{2}}{9} = 1\)
- \(\dfrac{(y - 3)^{2}}{11} - \dfrac{(x - 1)^{2}}{10} = 1\)
- \(\dfrac{(x + 4)^{2}}{16} - \dfrac{(y - 4)^{2}}{1} = 1\)
- \(\dfrac{(x+1)^2}{9} - \dfrac{(y-3)^2}{4} = 1\)
- \(\dfrac{(y+2)^2}{16} - \dfrac{(x-5)^2}{20} = 1\)
- \(\dfrac{(x-4)^2}{8} - \dfrac{(y-2)^2}{18} = 1\)
In Exercises 9 - 12, put the equation in standard form. Find the center, the lines which contain the transverse and conjugate axes, the vertices, the foci and the equations of the asymptotes.
- \(12x^{2} - 3y^{2} + 30y - 111 = 0\)
- \(18y^{2} - 5x^{2} + 72y + 30x - 63= 0\)
- \(9x^2-25y^2-54x-50y-169 = 0\)
- \(-6x^2+5y^2-24x+40y+26=0\)
In Exercises 13 - 18, find the standard form of the equation of the hyperbola which has the given properties.
- Center \((3, 7)\), Vertex \((3, 3)\), Focus \((3, 2)\)
- Vertex \((0, 1)\), Vertex \((8, 1)\), Focus \((-3, 1)\)
- Foci \((0, \pm 8)\), Vertices \((0, \pm 5)\).
- Foci \((\pm 5, 0)\), length of the Conjugate Axis \(6\)
- Vertices \((3,2)\), \((13,2)\); Endpoints of the Conjugate Axis \((8,4)\), \((8,0)\)
- Vertex \((-10, 5)\), Asymptotes \(y = \pm \frac{1}{2}(x - 6) + 5\)
In Exercises 19 - 28, find the standard form of the equation using the guidelines on page and then graph the conic section.
- \(x^2-2x-4y-11=0\)
- \(x^2 + y^2-8x+4y+11=0\)
- \(9x^2 + 4y^2-36x+24y + 36=0\)
- \(9x^2-4y^2-36x-24y-36=0\)
- \(y^2+8y-4x+16=0\)
- \(4x^2+y^2-8x+4=0\)
- \(4x^2+9y^2-8x+54y+49=0\)
- \(x^2 + y^2-6x+4y+14=0\)
- \(2x^2+ 4y^2+12x-8y+25=0\)
- \(4x^2-5y^2-40x-20y+160=0\)
- The graph of a vertical or horizontal hyperbola clearly fails the Vertical Line Test so the equation of a vertical of horizontal hyperbola does not define \(y\) as a function of \(x\). However, much like with circles, horizontal parabolas and ellipses, we can split a hyperbola into pieces, each of which would indeed represent \(y\) as a function of \(x\). With the help of your classmates, use your calculator to graph the hyperbolas given in Exercises 1 - 8 above. How many pieces do you need for a vertical hyperbola? How many for a horizontal hyperbola?
- The location of an earthquake’s epicenter \(-\) the point on the surface of the Earth directly above where the earthquake actually occurred \(-\) can be determined by a process similar to how we located Sasquatch in Example 8.5.5. Our technique works only for relatively small distances because we need to assume that the Earth is flat in order to use hyperbolas in the plane. The P-waves (“P” stands for Primary) of an earthquake in Sasquatchia travel at 6 kilometers per second. Station A records the waves first. Then Station B, which is 100 kilometers due north of Station A, records the waves 2 seconds later. Station C, which is 150 kilometers due west of Station A records the waves 3 seconds after that (a total of 5 seconds after Station A). Where is the epicenter?
- The notion of eccentricity introduced for ellipses in Section 8.4 is the same for hyperbolas in that we can define the eccentricity \(e\) of a hyperbola as
\[e = \dfrac{\mbox{distance from the center to a focus}}{\mbox{distance from the center to a vertex}}\nonumber\]
- With the help of your classmates, explain why \(e > 1\) for any hyperbola.
- Find the equation of the hyperbola with vertices \((\pm 3,0)\) and eccentricity \(e = 2\).
- With the help of your classmates, find the eccentricity of each of the hyperbolas in Exercises 1 - 8. What role does eccentricity play in the shape of the graphs?
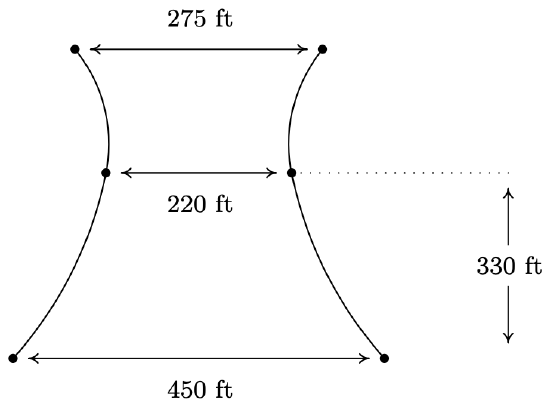
- In Section 7.3, we discussed paraboloids of revolution when studying the design of satellite dishes and parabolic mirrors. In much the same way, ‘natural draft’ cooling towers are often shaped as hyperboloids of revolution. Each vertical cross section of these towers is a hyperbola. Suppose the a natural draft cooling tower has the cross section below. Suppose the tower is 450 feet wide at the base, 275 feet wide at the top, and 220 feet at its narrowest point (which occurs 330 feet above the ground.) Determine the height of the tower to the nearest foot.
- With the help of your classmates, research the Cassegrain Telescope. It uses the reflective property of the hyperbola as well as that of the parabola to make an ingenious telescope.
- With the help of your classmates show that if \(Ax^2 + Cy^2 + Dx + Ey + F = 0\) determines a non-degenerate conic then
- \(AC < 0\) means that the graph is a hyperbola
- \(AC = 0\) means that the graph is a parabola
- \(AC > 0\) means that the graph is an ellipse or circle
Answers
- \(\dfrac{x^{2}}{16} - \dfrac{y^{2}}{9} = 1\)
Center \((0, 0)\)
Transverse axis on \(y = 0\)
Conjugate axis on \(x = 0\)
Vertices \((4, 0), (-4, 0)\)
Foci \((5, 0), (-5, 0)\)
Asymptotes \(y = \pm \frac{3}{4} x\)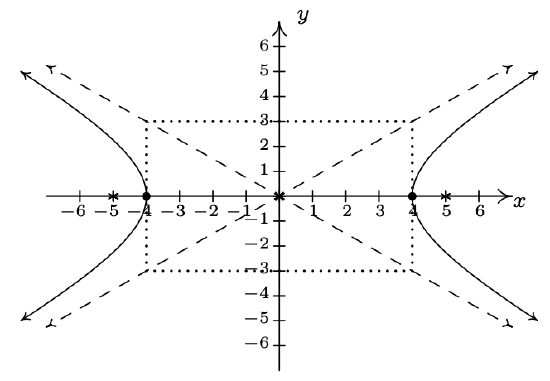
- \(\dfrac{y^{2}}{9} - \dfrac{x^{2}}{16} = 1\)
Center \((0, 0)\)
Transverse axis on \(x = 0\)
Conjugate axis on \(y = 0\)
Vertices \((0, 3), (0, -3)\)
Foci \((0, 5), (0, -5)\)
Asymptotes \(y = \pm \frac{3}{4} x\)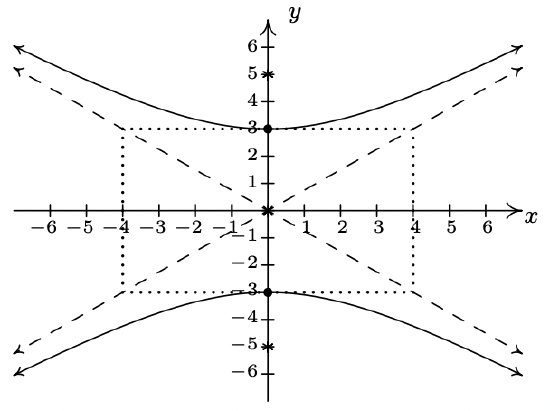
- \(\dfrac{(x - 2)^{2}}{4} - \dfrac{(y + 3)^{2}}{9} = 1\)
Center \((2, -3)\)
Transverse axis on \(y = -3\)
Conjugate axis on \(x = 2\)
Vertices \((0, -3), (4, -3)\)
Foci \((2 + \sqrt{13}, -3), (2 - \sqrt{13}, -3)\)
Asymptotes \(y = \pm \frac{3}{2}(x - 2) - 3\)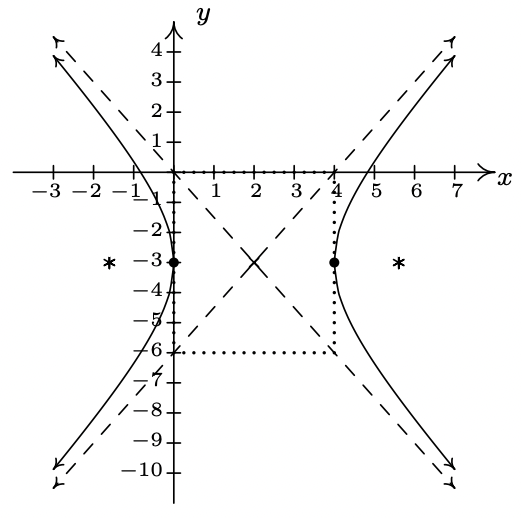
- \(\dfrac{(y - 3)^{2}}{11} - \dfrac{(x - 1)^{2}}{10} = 1\)
Center \((1, 3)\)
Transverse axis on \(x = 1\)
Conjugate axis on \(y = 3\)
Vertices \((1, 3 + \sqrt{11}), (1, 3 - \sqrt{11})\)
Foci \((1, 3 + \sqrt{21}), (1, 3 - \sqrt{21})\)
Asymptotes \(y = \pm \frac{\sqrt{110}}{10}(x - 1) + 3\)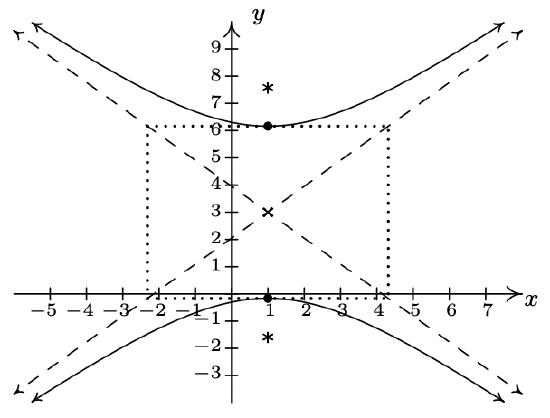
- \(\dfrac{(x + 4)^{2}}{16} - \dfrac{(y - 4)^{2}}{1} = 1\)
Center \((-4, 4)\)
Transverse axis on \(y = 4\)
Conjugate axis on \(x = -4\)
Vertices \((-8, 4), (0, 4)\)
Foci \((-4 + \sqrt{17}, 4), (-4 - \sqrt{17}, 4)\)
Asymptotes \(y = \pm \frac{1}{4}(x +4) +4\)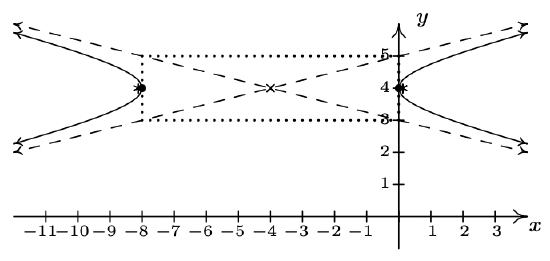
- \(\dfrac{(x+1)^2}{9} - \dfrac{(y-3)^2}{4} = 1\)
Center \((-1, 3)\)
Transverse axis on \(y=3\)
Conjugate axis on \(x=-1\)
Vertices \((2, 3), (-4, 3)\)
Foci \(\left(-1+\sqrt{13}, 3\right), \left(-1-\sqrt{13}, 3\right)\)
Asymptotes \(y = \pm \frac{2}{3} (x+1)+3\)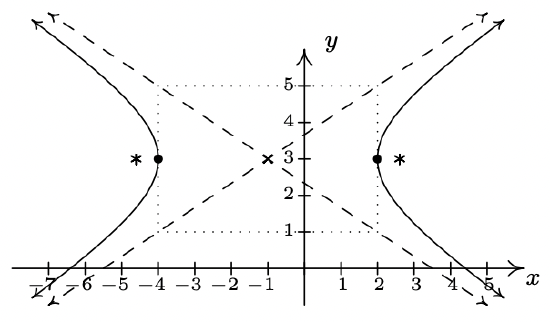
- \(\dfrac{(y+2)^2}{16} - \dfrac{(x-5)^2}{20} = 1\)
Center \((5, -2)\)
Transverse axis on \(x=5\)
Conjugate axis on \(y=-2\)
Vertices \((5,2), (5,-6)\)
Foci \(\left(5,4 \right), \left(5,-8\right)\)
Asymptotes \(y = \pm \frac{2\sqrt{5}}{5} (x-5)-2\)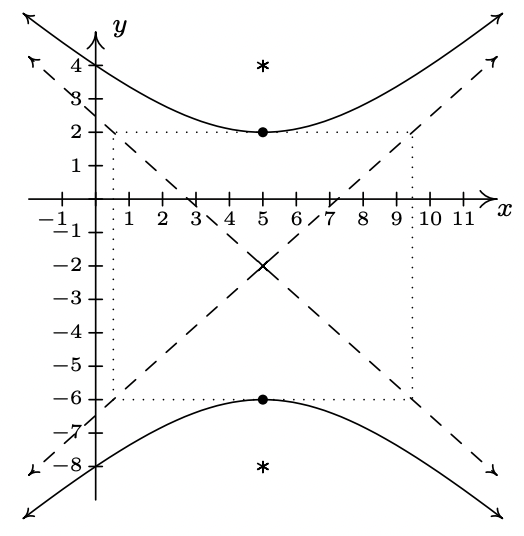
- \(\dfrac{(x-4)^2}{8} - \dfrac{(y-2)^2}{18} = 1\)
Center \((4, 2)\)
Transverse axis on \(y=2\)
Conjugate axis on \(x=4\)
Vertices \(\left(4+2\sqrt{2},2\right), \left(4-2\sqrt{2},2\right)\)
Foci \(\left(4+\sqrt{26},2 \right), \left(4-\sqrt{26},2\right)\)
Asymptotes \(y = \pm \frac{3}{2} (x-4)+2\)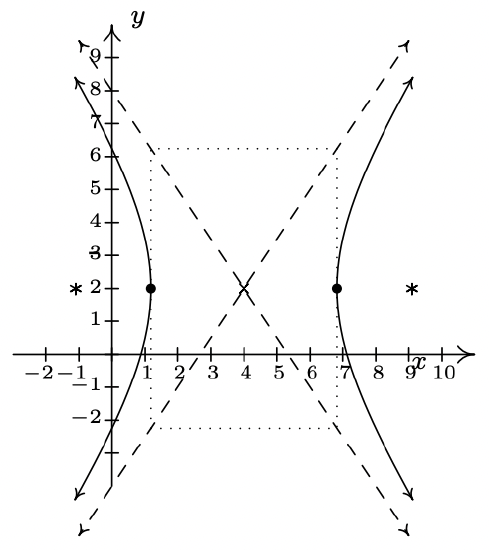
- \(\dfrac{x^{2}}{3} - \dfrac{(y - 5)^{2}}{12} = 1\)
Center \((0, 5)\)
Transverse axis on \(y = 5\)
Conjugate axis on \(x = 0\)
Vertices \((\sqrt{3}, 5), (-\sqrt{3}, 5)\)
Foci \((\sqrt{15}, 5), (-\sqrt{15}, 5)\)
Asymptotes \(y = \pm 2x + 5\) - \(\dfrac{(y + 2)^{2}}{5} - \dfrac{(x - 3)^{2}}{18} = 1\)
Center \((3, -2)\)
Transverse axis on \(x = 3\)
Conjugate axis on \(y = -2\)
Vertices \((3, -2 + \sqrt{5}), (3, -2 - \sqrt{5})\)
Foci \((3, -2 + \sqrt{23}), (3, -2 - \sqrt{23})\)
Asymptotes \(y = \pm \frac{\sqrt{10}}{6}(x - 3) - 2\) - \(\dfrac{(x-3)^{2}}{25} - \dfrac{(y+1)^{2}}{9} = 1\)
Center \((3, -1)\)
Transverse axis on \(y=-1\)
Conjugate axis on \(x=3\)
Vertices \((8, -1), (-2, -1)\)
Foci \(\left(3+\sqrt{34}, -1 \right), \left(3-\sqrt{34}, -1 \right)\)
Asymptotes \(y = \pm \frac{3}{5}(x - 3) - 1\) - \(\dfrac{(y+4)^{2}}{6} - \dfrac{(x+2)^{2}}{5} = 1\)
Center \((-2, -4)\)
Transverse axis on \(x=-2\)
Conjugate axis on \(y=-4\)
Vertices \(\left(-2,-4+\sqrt{6} \right), \left(-2,-4-\sqrt{6} \right)\)
Foci \(\left(-2, -4+\sqrt{11} \right), \left(-2, -4-\sqrt{11} \right)\)
Asymptotes \(y = \pm \frac{\sqrt{30}}{5}(x + 2) - 4\) - \(\dfrac{(y - 7)^{2}}{16} - \dfrac{(x - 3)^{2}}{9} = 1\)
- \(\dfrac{(x - 4)^{2}}{16} - \dfrac{(y - 1)^{2}}{33} = 1\)
- \(\dfrac{y^{2}}{25} - \dfrac{x^{2}}{39} = 1\)
- \(\dfrac{x^{2}}{16} - \dfrac{y^{2}}{9} = 1\)
- \(\dfrac{(x - 8)^{2}}{25} - \dfrac{(y - 2)^{2}}{4} = 1\)
- \(\dfrac{(x - 6)^{2}}{256} - \dfrac{(y - 5)^{2}}{64} = 1\)
- \((x-1)^2 = 4(y+3)\)
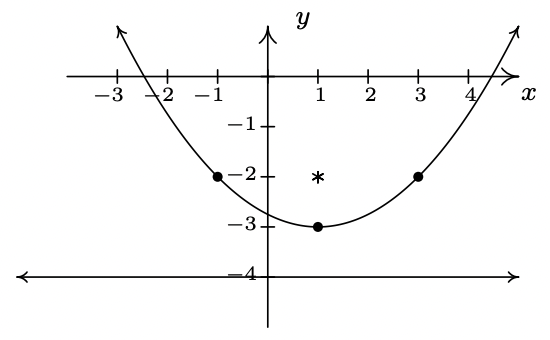
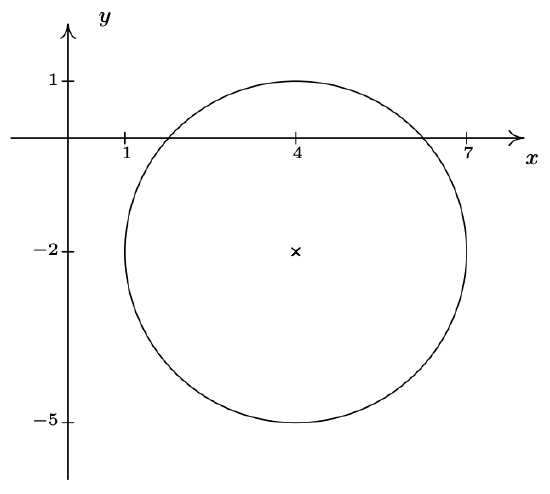
- \((x-4)^2+(y+2)^2 = 9\)
- \(\dfrac{(x - 2)^{2}}{4} + \dfrac{(y + 3)^{2}}{9} = 1\)
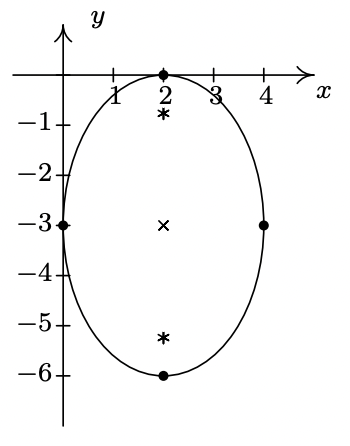
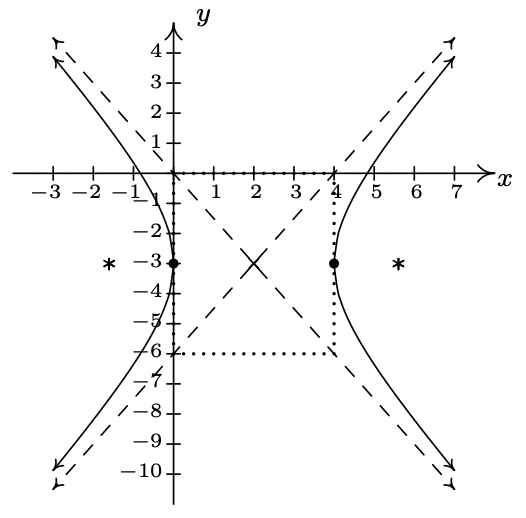
- \(\dfrac{(x - 2)^{2}}{4} - \dfrac{(y + 3)^{2}}{9} = 1\)
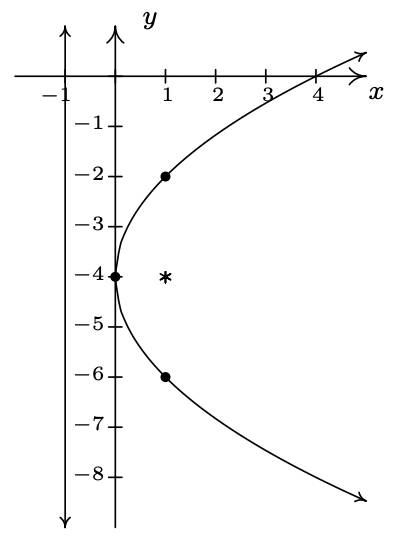
- \((y + 4)^{2} = 4x\)
-
\(\dfrac{(x-1)^2}{1}+\dfrac{y^2}{4}=0\)
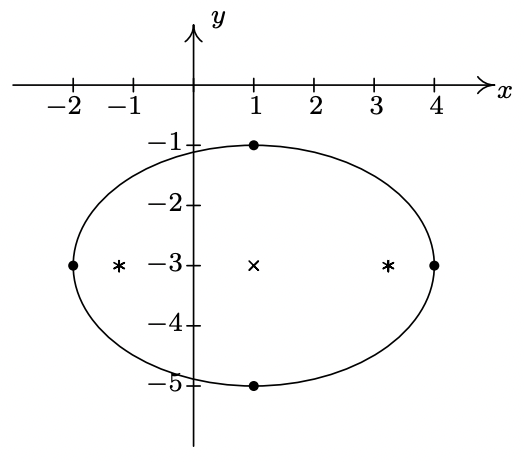
The graph is the point \((1,0)\) only. - \(\dfrac{(x-1)^2}{9}+\dfrac{(y+3)^2}{4} = 1\)
-
\((x-3)^2+(y+2)^2=-1\)
There is no graph. -
\(\dfrac{(x+3)^2}{2}+\dfrac{(y-1)^2}{1} = -\dfrac{3}{4}\)
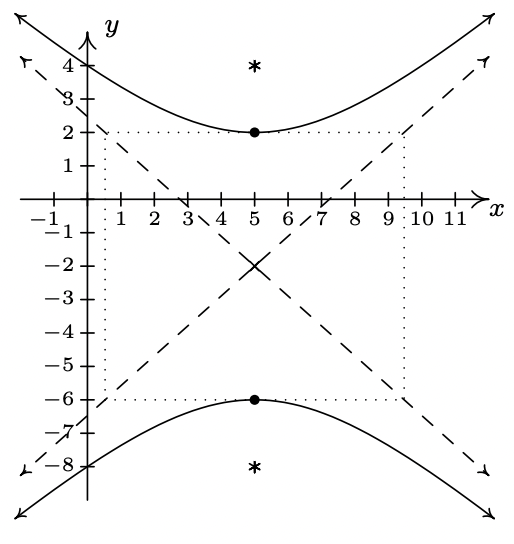
There is no graph. - \(\dfrac{(y+2)^2}{16} - \dfrac{(x-5)^2}{20} = 1\)
- By placing Station A at \((0, -50)\) and Station B at \((0, 50)\), the two second time difference yields the hyperbola \(\frac{y^{2}}{36} - \frac{x^{2}}{2464} = 1\) with foci A and B and center \((0, 0)\). Placing Station C at \((-150, -50)\) and using foci A and C gives us a center of \((-75, -50)\) and the hyperbola \(\frac{(x + 75)^{2}}{225} - \frac{(y + 50)^{2}}{5400} = 1\). The point of intersection of these two hyperbolas which is closer to A than B and closer to A than C is \((-57.8444, -9.21336)\) so that is the epicenter.
- \(\dfrac{x^2}{9} - \dfrac{y^2}{27} = 1\).
- The tower may be modeled (approximately) by \(\frac{x^2}{12100} - \frac{(y-330)^2}{34203} = 1\). To find the height, we plug in \(x = 137.5\) which yields \(y \approx 191\) or \(y \approx 469\). Since the top of the tower is above the narrowest point, we get the tower is approximately 469 feet tall.

