2.5: The Precise Definition of a Finite Limit at a Finite Number
- Page ID
- 116551
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- Describe the precise definition of a limit for both finite and infinite limits, at finite points and at infinity.
- Apply the epsilon-delta definition to find the limit of a function.
- Prove limits, both finite and infinite, using the precise definition of a limit.
- Describe the epsilon-delta definitions of one-sided limits.
- Use the epsilon-delta definition to prove the Limit Laws.
By now you have progressed from the very informal definition of a limit in the introduction of this chapter to the intuitive understanding of a limit. At this point, you should have a very strong intuitive sense of what the limit of a function means and how you can find it. In this section, we convert this intuitive idea of a limit into a formal definition using precise mathematical language. The formal definition of a limit is quite possibly one of the most challenging definitions you will encounter early in your study of calculus; however, it is well worth any effort you make to reconcile it with your intuitive notion of a limit. Understanding this definition is the key that opens the door to a better understanding of calculus.
Foreword: A Lesson in Patience
I have written this section to step you slowly through the concept, visualization, and understanding of the precise definition of a finite limit at a finite number (in addition to the other limits presented at the end of this section). Reading everything presented here, in the order it is presented, might seem exhaustingly lengthy; however, the presentation in this section is meticulously crafted to get you to a level of understanding necessary to succeed in calculus.
Quantifying Closeness
Before stating the formal definition of a limit, we must introduce a few preliminary ideas. Recall that the distance between two points \(a\) and \(b\) on a number line is given by |\(a−b\)|. From this point forward, we will constantly be using this interpretation.
- The statement |\(f(x)−L | \lt \epsilon \) may be interpreted as: The distance between \(f(x)\) and \(L\) is less than \(\epsilon\).
- The statement \(0<|x−a| \lt \delta\) may be interpreted as: \(x \neq a\) and the distance between \(x\) and \(a\) is less than \(\delta\).
In calculus, \(\delta\) and \(\epsilon\) (the Greek lowercase letters delta and epsilon, respectively) are inevitably going to be very small positive numbers. In fact, in most cases, they will be infinitesimally small (i.e., both \( \to 0^+ \)).
It is also important to look at the following equivalences for absolute value:
- The statement |\(f(x)−L| \lt \epsilon\) is equivalent to the statement \(L − \epsilon \lt f(x) \lt L + \epsilon\).
- The statement \(0\lt|x−a|\lt\delta\) is equivalent to the statement \(a−\delta\lt x\lt a+\delta\), where \(x\neq a\).
With these concepts of distances between values in hand, we need to introduce some language that will commonly be used as we discuss the precise definition of a limit.
A \(\delta\)-neighborhood centered at \(a\) is defined to be the interval \( (a - \delta, a) \cup (a, a + \delta)\) on the \(x\)-axis.
An \(\epsilon\)-neighborhood centered at \(L\) is defined to be the interval \((L - \epsilon, L + \epsilon)\) on the \(y\)-axis.
Do you see a difference between these two definitions? A \(\delta\)-neighborhood never includes its center (\(x = a\)), while an \(\epsilon\)-neighborhood always includes its center (\(y = L\)). Some people (myself included) call a \(\delta\)-neighborhood a punctured neighborhood.
The following Interactive Element might help you visualize key characteristics of \(\delta\)- and \(\epsilon\)-neighborhoods.
Interact: Move the sliders to adjust \(x = a\), \(\delta\), \(y = L\), and \(\epsilon\).
Observation: Neighborhoods are symmetric about their centers, and the \(\delta\)-neighborhood never includes its center.
The next example illustrates how this idea of "closeness" might be linked to the idea of a limit.
Using the concepts of "closeness" presented here (specifically, \(\delta\)- and \(\epsilon\)-neighborhoods), create a possible interpretation of
\[ \lim_{x \to 1}{\left(5x + 1\right)} = 6. \nonumber \]
Solution
Building the logic: Since \(f(x) = 5x + 1\) is approaching \(6\) as \(x\) is approaching \(1\), it seems like we are considering a group of \(x\)-values near \(1\) whose corresponding values on the function \(f(x)\) are approaching \(6\).
Tying this to intervals: In terms of intervals, it appears to be the case that we are saying all of the \(x\)-values in an interval (neighborhood) around \(x = 1\) lead to \(y\)-values in an interval (neighborhood) around \(y = 6\).
Tightening up the language: Perhaps this means that all the \(x\)-values in a \(\delta\)-neighborhood centered at \(x = 1\) lead to function values in an \(\epsilon\)-neighborhood centered at \(y = 6\).
Take note of the imprecise language in the solution of Example \(\PageIndex{1}\) - this is purposeful. We have not developed an actual definition of the limit yet, so we are trying to guess our way to a strong, infallible definition.
The \(\epsilon\) Gauntlet
Our interpretation of the meaning of the limit from Example \(\PageIndex{1}\),
\[ \lim_{x \to 1}{\left( 5x + 1 \right)} = 6, \nonumber \]
was, "all \(x\)-values in a \(\delta\)-neighborhood centered at \(x = 1\) lead to function values in an \(\epsilon\)-neighborhood centered at \(y = 6\)." Not only is this imprecise, but it is actually backwards.1 For now, let's focus on thinking of our interpretation in the correct order.
When handed the limit
\[ \lim_{x \to 1}{\left( 5x + 1 \right)} = 6, \nonumber \]
you are essentially being told that, no matter what sized \(\epsilon\)-neighborhood someone creates about \(y = 6\), you should be able to find a small enough \(\delta\)-neighborhood about \(x = 1\) so that the function, \(f(x) = 5x + 1\), is very close to the supposed limit \(6\) whenever \(x\) is close to \(1\). What do we mean by "close?" Hopefully, as long as our value of \(x\) is within the \(\delta\)-neighborhood, then the corresponding value of \(f(x)\) should be within the given \(\epsilon\)-neighborhood.
At this point, it's understandable if you had to read those last two paragraphs a few times. If you did, then good for you - you are practicing becoming a better critical thinker! Let's reward ourselves with a visualization that will help us grasp this idea of "\(\epsilon\) before \(\delta\)."
Interact: Grab the point on the \(x\)-axis at \(x = 1 + \delta\) and move it right and left.
Observation: We have been given a static \(\epsilon\)-neighborhood about \(y = 6\). Our job is to find a small enough \(\delta\)-neighborhood about \(x = 1\) so that \(f(x)\) is within the \(\epsilon\)-neighborhood for all values of \(x\) in our \(\delta\)-neighborhood.
The act of being handed a static \(\epsilon\) and challenged to find a corresponding \(\delta\) is called the \(\epsilon\) gauntlet. I call it this because it's as if someone is throwing a gauntlet at your feet and challenging you to find an appropriate \(\delta\)-neighborhood - if you dare!
Consider the limit
\[ \lim_{x \to 1}{\left( 5x + 1 \right)} = 6. \nonumber \]
Find an appropriate \(\delta\) so that all the function values, \(f(x) = 5x + 1\), lie within \(\epsilon = 0.001\) units of \(y = 6\) whenever \(x\) is within \(\delta\) units of \(x = 1\).
Solution
The \(\epsilon\) gauntlet has been thrown! Someone has issued the challenge and said that you cannot find a \(\delta\)-neighborhood about \(x = 1\) such that all of the corresponding functions values land in their very small \(\epsilon\)-neighborhood about \(y = 6\). The size of their given \(\epsilon\) neighborhood is \(0.001\).
The given \(\epsilon\)-neighborhood rises from
\(y = 6 - \epsilon = 6 - 0.001 = 5.999\)
to
\(y = 6 + \epsilon = 6 + 0.001 = 6.001\).
Solving \(5.999 = 5x + 1\) and \(6.001 = 5x + 1\), we get \(x = 0.9998\) and \(x = 1.0002\), respectively. This means that as long as \(x \in (0.9998,1) \cup (1,1.0002)\), \(f(x) \in (5.999, 6.001)\).
To compute the value of \(\delta\), we consider the "length" of each subinterval on the \(x\)-axis. The first is \((0.9998,1)\). This has a length of \(0.0002\). Likewise, the subinterval \((1,1.0002)\) has a length of \(0.0002\). Thus, we choose \(\delta = 0.0002\).2
Whenever \(x\) is within \(\delta = 0.0002\) units of \(1\) on the \(x\)-axis, the corresponding function value, \(f(x)\), must therefore be within \(\epsilon = 0.001\) units of \(y = 6\).
A visual to confirm this is in Figure \(\PageIndex{1}\) below
Interact: Drag either point to confirm the computed \(\delta\)-neighborhood.
1 I will explain why in a few short paragraphs from now.
2 The idea of the "length" of a subinterval is a bit loose. In reality, we are measuring the radii from the center, \( x = 1 \), to the edge of each of these subintervals. To find the "length" of the interval \( \left( x_L, x_R \right) \) (I use the notation \( L \) for the \( x \)-value at the left edge and \( R \) for the \( x \)-value of the right edge), we compute \[ x_R - x_L. \nonumber \]This concept (right minus left) will become of utmost importance when we learn about integrals and their applications.
The Precise Definition of a Finite Limit at a Finite Number
With these clarifications, we can state the formal \( \epsilon-\delta \) definition of a finite limit at a finite number.
Let \(f(x)\) be defined for all \(x \neq a\) over an open interval containing \(a\), and let \(L\) be a real number. We say
\[\lim_{x \to a}f(x)=L \nonumber \]
if for every \( \epsilon >0\), there exists a \( \delta >0\), such that if \(0<|x−a|< \delta \), then \(|f(x)−L|< \epsilon \).
Stated with symbolic logic,
\[\lim_{x \to a}f(x)=L \nonumber \]
means
\[ \forall \epsilon \gt 0, \quad \exists \delta \gt 0 \ni \nonumber \]
\[ 0 \lt |x - a| \lt \delta \implies |f(x) - L| \lt \epsilon. \nonumber \]
You are probably not used to symbolic logic, so let's define those symbols.
| Symbol | Meaning |
|---|---|
| \( \forall \) | "for all" or "for each" or "for every" |
| \( \exists \) | "there exists" or "there is" |
| \( \implies \) | "implies" or "then" |
| \( \ni \) | "such that" or "so that" |
The symbol \( \ni \) is used frequently in symbolic logic for "such that", however, many mathematicians do not use it for that purpose. Check with your instructor to see what logic symbol they prefer (many just avoid the confusion entirely and use "s.t.").
Critically Analyzing the Structure of the Precise Definition of a Finite Limit at a Finite Number
This definition may seem rather complex from a mathematical point of view, but it becomes easier to understand if we break it down phrase by phrase. The statement itself involves something called a universal quantifier (for every \( \epsilon >0\), or \( \forall \epsilon \gt 0 \)), an existential quantifier (there exists a \( \delta >0\), or \( \exists \delta \gt 0 \)), and, last, a conditional statement (if \(0<|x−a|< \delta \), then \(|f(x)−L|< \epsilon )\). Let’s take a look at Table \(\PageIndex{1}\), which breaks down the definition and translates each part.
| Definition | Symbolic Logic | Translation |
|---|---|---|
| For every \( \epsilon >0\), | \( \forall \epsilon \gt 0 \) | For every positive distance \( \epsilon \) from \(L\), |
| there exists a \( \delta >0\), | \( \exists \delta \gt 0 \) | there is a positive distance \( \delta \) from \(a\), |
| such that | \( \ni \) | such that |
| if \(0<|x−a|< \delta \), then \(|f(x)−L|< \epsilon \). | \( 0 \lt |x - a| \lt \delta \implies |f(x) - L| \lt \epsilon \) | if \(x\) is within \( \delta \) units of \(a\) and \(x \neq a\), then \(f(x)\) is within \(\epsilon\) units of \(L\). |
Graphically Interpreting the Precise Definition of a Finite Limit at a Finite Number
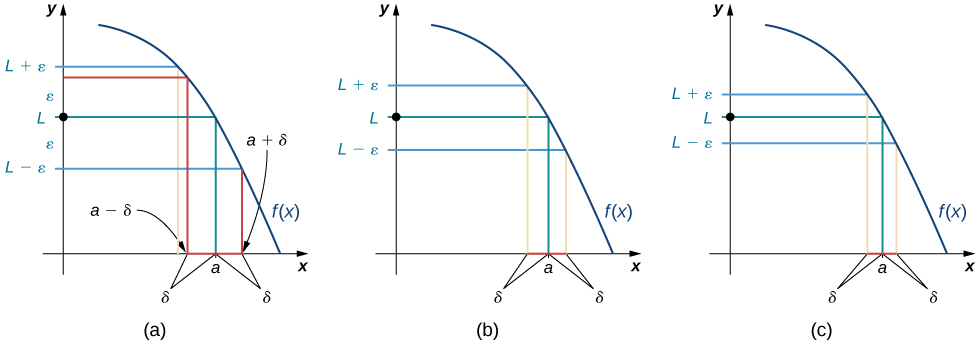
We can get a better handle on this definition by looking at the definition geometrically. Figure \(\PageIndex{1}\) shows possible values of \( \delta \) for various choices of \( \epsilon >0\) for a given function \(f(x)\), a number \(a\), and a limit \(L\) at \(a\). Notice that as we choose smaller values of \( \epsilon \) (the distance between the function and the limit), we can always find a \( \delta \) small enough so that if we have chosen an \(x\) value within \( \delta \) of \(a\), then the value of \(f(x)\) is within \( \epsilon \) of the limit \(L\).
The Importance of Scratch Work
Your instructor has likely presented proofs in class that were clean, succinct, and well-polished. Did she do so out of thin air? Is she just a genius that can throw together any logical argument without flaw? Nope!
Before delving into examples, it is incredibly important to understand that mathematicians (and, therefore, you) do not magically write clean proofs from step 1 to step 100 without doing a bit (or quite a bit) of scratch work. Scratch work is where the real magic happens. It is where you allow yourself to think creatively, experiment with options, and discover pathways to the proof without fear of judgment and nasty comments from someone looking over your shoulder. The proof, on the other hand, is a cleaned-up version of the scratch work with logically deductive steps and no flaws.
To understand how scratch work is done (and why we need it), you need to first have a solid understanding of the structure of a theorem. Theorems come in many forms, but the form that is relevant to our current task is the "If..., then..." statement. An "If..., then..." statement is a theorem (or conjecture) that is either
- written as "If \( P \) is true, then \( Q \) is true," where \( P \) and \( Q \) are simple statements, or
- is written in a form that can be rewritten as the form above.
For an example of each, consider the following:
- "If it's raining, then it's cloudy."
- "It's only raining when it is cloudy."
These two conjectures are the same; however, in mathematics, it's often easier to rewrite conjectures (or theorems) in the first, "If..., then...," format.
The "If" part of a theorem is known as the antecedent and the "then" part is called the consequent. In the example above, the antecedent is "it's raining" and the consequence is "it's cloudy." These parts to a theorem will be important as we move forward.
Once we have rewritten the theorem in "If..., then..." format, it can be visualized as a 1000-piece puzzle in a box. Conceptually, the theorem can be thought of as follows:
If you can fit all the pieces together correctly, then the result will look like the picture on the box.
For reference, the antecedent is "you can fit all the pieces of the puzzle together correctly." The consequent is "the result will precisely match the picture on the box."
The scratch work in the puzzle-building process is to constantly reference the picture on the box (the consequent) to see what you want to end up with. You have a blue corner piece in your hand and, looking at the box, you see the only corner that is blue is the upper-right corner. So you place it there. You notice on the box that not too far down from that corner is a creepy clown with red hair (important: all clowns are creepy). Therefore, you start gathering all the puzzle pieces that look to have red hair. And on the process goes.
This is very much akin to working backwards, or reverse engineering, the puzzle-solving process, and this is precisely what we do in scratch work.
Scratch work often starts by assuming we have arrived at the consequent. We then work backwards to see how we got to the consequent. We hope this will eventually, with some possible conditions, allow us to work all the way back to the antecedent.
We ask ourselves, "If I arrived at the picture on the box, what had to be true about the last piece I fit into the puzzle? And what does that mean about the piece I fit in prior to that?" And so on.
In each of the proofs throughout this section, I will demonstrate what good scratch work in mathematics looks like. Please pay close attention to that and the proof structure.
Proving Finite Limits at Finite Numbers (symmetric \( \delta \)-neighborhood)
We will take our time going through this first example, but as we progress, the amount of "discussion" within examples will decrease.
Prove
\[ \displaystyle \lim_{x \to 1}{(5x+1)} = 6 \nonumber. \]
Solution
A very important initial step is to rewrite this limit as the precise definition of a limit.
\[ \displaystyle \lim_{x \to 1}{(5x+1)} = 6 \nonumber \]
means that
\[ \forall \epsilon \gt 0, \quad \exists \delta \gt 0 \quad \ni \nonumber \]
\[ 0 \lt |x - 1| \lt \delta \implies |(5x + 1) - 6| \lt \epsilon. \nonumber \]
Read alternatively: No matter what \( \epsilon \gt 0 \) that someone hands us, it is our job to find a \( \delta \gt 0 \) (that almost always relies on the value of \( \epsilon \) we were given) so that
If \( 0 \lt |x - 1| \lt \delta \), then we can guarantee that \( |(5x + 1) - 6| \lt \epsilon. \)
SCRATCH WORK
Just like we would reference the puzzle box to see where we want to arrive, we are going to look at the consequent of our "If..., then..." statement to see where we need our proof to finish.
In our proof, we want to arrive at
\[ |(5x + 1) - 6| \lt \epsilon \quad \left( \text{consequent} \right) \nonumber \]
given that
\[ 0 \lt |x - 1| \lt \delta. \quad \left( \text{antecedent} \right) \nonumber \]
Working backwards from the consequent, and trying to arrive at the antecedent, we get
\[ \begin{array}{rcl}
|(5x + 1) - 6| \lt \epsilon & \implies & |5x - 5| \lt \epsilon \\
& \implies & |5(x - 1)| \lt \epsilon \\
& \implies & |5| \cdot |x - 1| \lt \epsilon \\
& \implies & 5 \cdot |x - 1| \lt \epsilon \\
& \implies & |x - 1| \lt \dfrac{\epsilon}{5} \\
\end{array} \nonumber \]
So we can see that, if we want to arrive at the consequent (\( |(5x + 1) - 6| \lt \epsilon \)), a superb choice for \( \delta \) in our antecedent (\( 0 \lt |x - 1| \lt \delta \)) is \( \epsilon/5 \). We now know how to "correctly put this puzzle together."
Note, the structure of the proof should be closely aligned with the structure of the precise definition of the limit. That is, it should flow in the following direction:
\[ \forall \epsilon \gt 0, \quad \exists \delta \gt 0 \quad \ni \nonumber \]
\[ 0 \lt |x - 1| \lt \delta \implies |(5x + 1) - 6| \lt \epsilon. \nonumber \]
PROOF
\( \forall \epsilon \gt 0 \), choose \( \delta = \dfrac{\epsilon}{5} \). Therefore, if \( 0 \lt |x - 1| \lt \delta \), then
\[ \begin{array}{crclr}
& |x - 1| & \lt & \dfrac{\epsilon}{5} & \left( \text{Substitution} \right) \\
\implies & 5|x - 1| & \lt & \epsilon & \\
\implies & |5x - 5| & \lt & \epsilon & \\
\implies & |(5x +1) - 6| & \lt & \epsilon & \\
\implies & |f(x) - L| & \lt & \epsilon & \left( \text{Substitution} \right) \\
\end{array} \nonumber \]
Thus, we have proved the limit
\[ \displaystyle \lim_{x \to 1}{(5x+1)} = 6. \nonumber \]
Before moving on to the next example, let's take some lessons from Example \( \PageIndex{3} \).
- We always need to do scratch work when attempting a proof. Not doing so is akin to not looking at the cover of the puzzle box before attempting to piece a puzzle together.
- The scratch work starts with the consequent and works backwards to (hopefully) arrive at the antecedent.
- We have no control over what \( \epsilon \) they hand us, but \( \delta \) will almost always be a function of \( \epsilon \) (the single exception is when proving the limit of a constant function).
- The structure of our proof will be closely aligned with the language of the precise definition of a limit with the exception that we will not be saying, "there exists a \( \delta \gt 0 \)," but rather, "let \( \delta =... \)" because we actually found a workable \( \delta \) in our scratch work.
As we progress into the next example, we streamline our language and our work. Additionally, we write our scratch work off to the side so that the reader can immediately see our proof (the scratch work is provided for you, the student, to demonstrate what proper scratch work looks like).
Prove
\[ \displaystyle \lim_{x \to -2/3}{(9x^2 +12x - 7)} = -11 \nonumber. \]
Solution
|
PROOF For any given positive value of \(\epsilon\), let \( \delta = \dfrac{\sqrt{\epsilon}}{3} \). If it is the case that \( 0 \lt \left|x - \left(-\dfrac{2}{3}\right)\right| \lt \delta \), then \[ \begin{array}{crcl} Thus, we have proved the limit \[ \displaystyle \lim_{x \to -2/3}{(9x^2 +12x - 7)} = -11 \nonumber. \] |
SCRATCH WORK We want to arrive at \[ |(9x^2 +12x - 7) - (-11)| \lt \epsilon \quad \left( \text{consequent} \right) \nonumber \] given that \[ 0 \lt \left|x - \left(-\dfrac{2}{3}\right) \right| \lt \delta. \quad \left( \text{antecedent} \right) \nonumber \] Working backwards from the consequent, and trying to arrive at the antecedent, we get \[ \begin{array}{rcl} |
Let's add on to our list of lessons by looking at the previous example.
- We have some flexibility in the language used during the proof. You don't always have to write, "\( \forall \epsilon \gt 0 \)." Instead, you could use language.
Prove
\[ \displaystyle \lim_{x \to 2}\;(3x−2)=4 \nonumber \]
- Hint
-
You should eventually arrive at \( \delta =\frac{ \epsilon }{3}\).
Proving Finite Limits at Finite Numbers (non-symmetric \( \delta \)-neighborhoods)
In Examples \(\PageIndex{3}\) and \(\PageIndex{4}\), the proofs were fairly straightforward, since the \( \delta \)-neighborhoods were symmetric about \( x = a \). However, what happens if the \( \delta \)-neighborhood is not symmetric about \( x = a \)? What does that question even mean?
Consider the function
\[ f(x) = x^2 \nonumber \]
as \( x \to 2 \). From Figure \( \PageIndex{2} \), we can see that, for a given \( \epsilon \gt 0 \), we create an interval of sufficient \( x \)-values on the \( x \)-axis whose function values land in the interval \( (4 - \epsilon,4 + \epsilon) \).
![This graph shows how to find delta geometrically for a given epsilon for the above proof. First, the function f(x) = x^2 is drawn from [-1, 3]. On the y axis, the proposed limit 4 is marked, and the line y=4 is drawn to intersect with the function at (2,4). For a given epsilon, point 4 + epsilon and 4 – epsilon are marked on the y axis above and below 4. Blue lines are drawn from these points to intersect with the function, where pink lines are drawn from the point of intersection to the x axis. These lines land on either side of x=2. Next, we solve for these x values, which have to be positive here. The first is x^2 = 4 – epsilon, which simplifies to x = sqrt(4-epsilon). The next is x^2 = 4 + epsilon, which simplifies to x = sqrt(4 + epsilon). Delta is the smaller of the two distances, so it is the min of (2 – sqrt(4 – epsilon) and sqrt(4 + epsilon) – 2).](https://math.libretexts.org/@api/deki/files/12354/2.5.2.png?revision=1)
Figure \(\PageIndex{2}\): This graph shows how we find \(\delta\) geometrically for a given \(\epsilon\) given \( f(x) = x^2 \).
The size of the interval of acceptable values to the left of \( x = 2 \) looks to be slightly greater than the size of the interval of acceptable values to the right of \( x = 2 \). If we let \( \delta_L \) be the size of the interval to the left, and \( \delta_R \) be the size of the interval to the right, then as long as \( x \in (2 - \delta_L, 2) \cup (2, 2 + \delta_R) \), we know \( f(x) = x^2 \in (4 - \epsilon, 4 + \epsilon) \).
However, \( \delta \)- and \( \epsilon \)- neighborhoods are defined to be symmetric about their centers. We have an issue because it looks as though our \( \delta \)-neighborhood is not symmetric about \( x = 2 \) (as an aside, the \( \epsilon \)-neighborhoods will always be symmetric about their centers, so you don't have to worry about those). What do we do?
If given two choices for \( \delta \), always take the smaller. For example, if we performed the computations given \( \epsilon = 2 \) (a gratuitously large \( \epsilon \)-neighborhood), we would find \( \delta_L \approx 0.586 \) and \( \delta_R \approx 0.449 \). This means that for \( x \in (1.414, 2) \cup (2, 2.449) \), \( f(x) \in (2, 6) \).
If all of the \( x \)-values in the interval \( (1.414, 2) \cup (2, 2.449) \) have this property, then all of the \( x \)-values in a smaller subinterval of \( (1.414, 2) \cup (2, 2.449) \) must also share this same property. Therefore, if we "tighten-up" the interval to be symmetric about \( x = 2 \) using the minimum of \( \delta_L \) and \( \delta_R \), the resulting set of \( x \)-values should still map to function values within the given \( \epsilon \)-neighborhood about \( y = 4 \).
\[ \delta_L \approx 2 - 1.414 = 0.586 \quad \text{and} \quad \delta_R \approx 2.449 - 2 = 0.449. \nonumber \]
Hence, we choose \( \delta \) to be \[ \min\{ \delta_L, \delta_R\} \approx \min\{ 0.586, 0.449\} = 0.449. \nonumber \]
While investigating the following limit, someone states that you couldn't possibly find an appropriate \( \delta \)-neighborhood given \( \epsilon = 0.5 \). With the use of graphing technology, prove them wrong.
\[ \displaystyle \lim_{x \to -2}{\left( e^{x+2} + 3 \sin{\left(\dfrac{\pi}{12}x\right)} + 2\right)} = 1.5 \nonumber \]
Solution
This style of problem displays whether or not someone truly understands the language translation of the precise definition of a finite limit at a finite number. Remember, this limit is equivalent to saying,
\[ \forall \epsilon \gt 0, \quad \exists \delta \gt 0 \ni \nonumber \]
\[ 0 \lt |x + 2| \lt \delta \implies \left|\left( e^{x+2} + 3 \sin{\left(\dfrac{\pi}{12}x\right)} + 2\right) - 1.5\right| \lt \epsilon. \nonumber \]
However, reading this in language and allowing \( \epsilon = 0.5 \), we can rephrase this as follows: Given \( \epsilon = 0.5 \), we should be able to find a positive distance, \( \delta \), from \( x = -2 \), such that if \( x \) is within \( \delta \) units of \( -2 \), then \( f(x) \) is within \( 0.5 \) units of \( 1.5 \).
Since we are allowed graphing technology, let's use Desmos to graph \( f(x) = e^{x+2} + 3 \sin{\left(\dfrac{\pi}{12}x\right)} + 2 \), \( y = 1.5 \), and the edges of our provided \( \epsilon \)-neighborhood \( y = 1.5 \pm 0.5 \).

Figure \( \PageIndex{3} \)
It is now our job to find an appropriately-sized \( \delta \)-neighborhood about \( x = -2 \) so that all \( x \)-values from this \( \delta \)-neighborhood lead to function values in the interval \( (1.5 - 0.5, 1.5 + 0.5) \). Desmos automatically computes intersections for us, so all we need to do is click on the points where the function meets the upper and lower horizontal lines (the red-dashed lines).

Figure \( \PageIndex{4} \)
You can see I also graph the vertical lines at these intersection points to further help our visual. Therefore, as long as \( x \in (-2.33, -2) \cup (-2, -1.729) \), the function values look to satisfy the requirement by our challenger. That is, on the interval \( (-2.33, -2) \cup (-2, -1.729) \), \( |f(x) - 1.5 | \lt 0.5 \).
So how large should our \( \delta \)-neighborhood be?
The size of the interval to the left of \( -2 \) is approximately \( -2 - (-2.33) = 0.33\) and the size of the interval to the right of \( -2 \) is approximately \( -1.729 - (-2) = 0.271 \). I say "approximately" because Desmos only returns a maximum of three digits on their graphs.
When given the option of two values for \( \delta \), we always choose the smaller. Thus, we should choose \( \delta = 0.271 \) (in fact, due to rounding errors, we might want to choose \( \delta \) slightly smaller... say, \( 0.270 \)).
The geometric investigation we just performed provides insight into the formal definition of the limit that is invaluable. However, an algebraic approach is the primary tool used in proofs of statements about limits. In Example \(\PageIndex{6}\), we take on a purely algebraic approach to prove a limit involving non-symmetric values of \( \delta \).
Prove that
\[ \displaystyle \lim_{x \to −1}{(x^2−2x+3)} = 6. \nonumber \]
Solution
|
PROOF \(\forall \epsilon \gt 0 \), I will choose \( \delta = \min\left\{ 1, \dfrac{\epsilon}{5} \right\} \). If \( 0 \lt \left|x - (-1)\right| \lt \delta \), then \[ |x + 1| \lt 1 \text{ and } |x + 1| \lt \dfrac{\epsilon}{5} \nonumber \] Since \( |x + 1| \lt 1 \), \[ \begin{array}{rcl} Additionally, since \( |x + 1| \lt \dfrac{\epsilon}{5} \), \[ \begin{array}{rcl} Thus, we have proved the limit \[ \displaystyle \lim_{x \to -1}{(x^2 - 2x + 3)} = 6 \nonumber. \] |
SCRATCH WORK We want to arrive at \[ |(x^2−2x+3) - 6| \lt \epsilon \quad \left( \text{consequent} \right) \nonumber \] given that \[ 0 \lt \left|x - (-1) \right| \lt \delta. \quad \left( \text{antecedent} \right) \nonumber \] Working backwards from the consequent, and trying to arrive at the antecedent, we get \[ \begin{array}{rcl} We want to keep \( |x + 1| \) because that is part of the antecedent; however, that \( |x - 3| \) needs to be replaced with (hopefully) a constant. We will need to judiciously build a bound for \( |x - 3| \). Building the Bound for \( |x - 3| \) Since \( x \to -1 \), it's fair to say that \( -2 \lt x \lt 0 \). We are assuming here that \( \delta_1 = 1 \). That is, we are assuming \( x \) is within \( 1 \) unit of \( -1 \). This means that, for the remainder of this argument (and for the proof), we will not allow our \( \delta \)-neighborhood to be larger than \( 1 \). With this assumption, and subtracting \( 3 \) from all three sides of the inequality, we get \[ -5 \lt x - 3 \lt -3. \nonumber \] Taking the absolute value of all three sides, we get \[ 5 \gt |x - 3| \gt 3. \nonumber \] Therefore, if \( x \in (-2 , 0) \), we know that \( |x - 3| \) can be, at maximum, \( 5 \). This will be our bound on \( |x - 3| \). That is, \[ |x - 3| \lt 5. \nonumber \] Using the Bound Going back to our work, we ended with \[ |(x - 3)(x + 1)| = |x - 3| \cdot |x + 1| \lt \epsilon; \nonumber \] however, we know that, in the very worst-case scenario, \( |x - 3| \) is still less than \( 5 \). Therefore, \[ \begin{array}{rcl} Hence, \[ 5|x + 1| \lt \epsilon \implies |x + 1| \lt \dfrac{\epsilon}{5}. \nonumber \] This shows us that \( \delta_2 = \dfrac{\epsilon}{5} \). We can now begin the proof. |
Prove that \(\displaystyle \lim_{x \to 1}x^2=1\).
- Hint
-
Use Example \(\PageIndex{3}\) as a guide.
- Answer
-
\(∣x^2−1∣=|x−1| \cdot |x+1|< \epsilon /3 \cdot 3= \epsilon \)
You will find that, in general, the more complex a function, the more likely it is that the algebraic approach is the easiest to apply. The algebraic approach is also more useful in proving statements about limits.
Proving Limit Laws
We now demonstrate how to use the \( \epsilon-\delta \) definition of a limit to construct a rigorous proof of one of the Limit Laws. The Triangle Inequality is used at a key point of the proof, so we first review this key property of absolute value.
If \(a\) and \(b\) are any real numbers, then \(|a+b| \leq |a|+|b|\).
Recall: If \(\displaystyle \lim_{x \to a}f(x)=L\) and \(\displaystyle \lim_{x \to a}g(x)=M\), then \(\displaystyle \lim_{x \to a}\;(f(x)+g(x))=L+M\).
Proof
Let \( \epsilon \gt 0\). Choose \( \delta _1 \gt 0\) so that if \(0 \lt |x−a| \lt \delta _1\), then \(|f(x)−L| \lt \epsilon /2\), and choose \( \delta _2 \gt 0\) so that if \(0 \lt |x−a| \lt \delta _2\), then \(|g(x)−M| \lt \epsilon /2\). Let \( \delta = \min\{ \delta _1, \delta _2\}\). If \(0 \lt |x−a| \lt \delta \), then
\[ 0 \lt |x−a| \lt \delta _1 \text{ and } 0 \lt |x−a| \lt \delta _2. \nonumber \]
Hence,
\[\begin{array}{rcl}
|(f(x)+g(x)) − (L+M)| & = & |(f(x)−L) + (g(x)−M)| \\
& \leq & |f(x)−L|+|g(x)−M| \\
& \lt & \frac{ \epsilon }{2}+\frac{ \epsilon }{2} \\
& = & \epsilon \\
\end{array} \nonumber \]
Q.E.D.
Showing a Limit Does Not Exist
We now explore what it means for a limit not to exist. The limit \(\displaystyle \lim_{x \to a}f(x)\) does not exist if there is no real number \(L\) for which \(\displaystyle \lim_{x \to a}f(x)=L\). Thus, for all real numbers \(L\), \(\displaystyle \lim_{x \to a}f(x) \neq L\). To understand what this means, we look at each part of the definition of \(\displaystyle \lim_{x \to a}f(x)=L\) together with its opposite. A translation of the definition is given in Table \(\PageIndex{2}\).
| Definition | Opposite |
|---|---|
| For every \( \epsilon >0\), | There exists \( \epsilon >0\) so that |
| there exists a \( \delta >0\), so that | for every \( \delta >0\), |
| if \(0<|x−a|< \delta \), then \(|f(x)−L|< \epsilon \). | there is an \(x\) satisfying \(0<|x−a|< \delta \) so that \(|f(x)−L| \geq \epsilon \). |
Finally, we may state what it means for a limit not to exist. The limit \(\displaystyle \lim_{x \to a}f(x)\) does not exist if for every real number \(L\), there exists a real number \( \epsilon >0\) so that for all \( \delta >0\), there is an \(x\) satisfying \(0<|x−a|< \delta \), so that \(|f(x)−L| \geq \epsilon \). Let’s apply this in Example \(\PageIndex{7}\) to show that a limit does not exist.
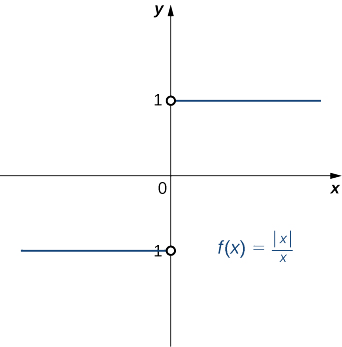
Show that \(\displaystyle \lim_{x \to 0}\frac{|x|}{x}\) does not exist. The graph of \(f(x)=|x|/x\) is shown here:
Solution
Suppose that \(L\) is a candidate for a limit. Choose \( \epsilon =1/2\).
Let \( \delta >0\). Either \(L \geq 0\) or \(L<0\). If \(L \geq 0\), then let \(x=− \delta /2\).
Thus,
\(|x−0|=∣−\frac{ \delta }{2}−0∣=\frac{ \delta }{2}< \delta \)
and
\(\left|\frac{∣−\frac{ \delta }{2}∣}{−\frac{ \delta }{2}}−L\right|=|−1−L|=L+1 \geq 1>\frac{1}{2}= \epsilon \).
On the other hand, if \(L<0\), then let \(x= \delta /2\). Thus,
\(|x−0|=∣\frac{ \delta }{2}−0∣=\frac{ \delta }{2}< \delta \)
and
\(\left|\frac{∣\frac{ \delta }{2}∣}{\frac{ \delta }{2}}−L\right|=|1−L|=|L|+1 \geq 1>\frac{1}{2}= \epsilon \).
Thus, for any value of \(L\), \(\displaystyle \lim_{x \to 0}\frac{|x|}{x} \neq L.\)
One-Sided Limits
Just as we first gained an intuitive understanding of limits and then moved on to a more rigorous definition of a limit, we now revisit one-sided limits. To do this, we modify the \( \epsilon-\delta \) definition of a limit to give formal \( \epsilon-\delta \) definitions for limits from the right and left at a point. These definitions only require slight modifications from the definition of the limit. In the definition of the limit from the right, the inequality \(0 \lt x−a \lt \delta \) replaces \(0 \lt |x−a| \lt \delta \), which ensures that we only consider values of \(x\) that are greater than (to the right of) \(a\). Similarly, in the definition of the limit from the left, the inequality \(− \delta \lt x−a \lt 0\) replaces \(0 \lt |x−a| \lt \delta \), which ensures that we only consider values of \(x\) that are less than (to the left of) \(a\).
Limit from the Right: Let \(f(x)\) be defined over an open interval of the form \((a,b)\) where \(a<b\). Then
\[\lim_{x \to a^+}f(x)=L \nonumber \]
if for every \( \epsilon >0\), there exists a \( \delta >0\), such that if \(0<x−a< \delta \), then \(|f(x)−L|< \epsilon \).
Limit from the Left: Let \(f(x)\) be defined over an open interval of the form \((b,c)\) where \(b<c\). Then,
\[\lim_{x \to c^−}f(x)=L \nonumber \]
if for every \( \epsilon >0\),there exists a \( \delta >0\) such that if \( − \delta <x−c<0\), then \(|f(x)−L|< \epsilon \).
Prove that
\[\lim_{x \to 4^+}\sqrt{x−4}=0.\nonumber \]
Solution
|
PROOF For \(\epsilon \gt 0\), let \( \delta = \epsilon^2 \). If \( 0 \lt x - 4 \lt \delta \), then \[ \begin{array}{crcl} Thus, we have proved the limit \[\lim_{x \to 4^+}\sqrt{x−4}=0.\nonumber \] |
SCRATCH WORK We want to arrive at \[ |\sqrt{x−4} - 0| \lt \epsilon \quad \left( \text{consequent} \right) \nonumber \] given that \[ 0 \lt x - 4 \lt \delta. \quad \left( \text{antecedent} \right) \nonumber \] (Remember, since \( x \to 4^+ \), \( x \gt 4 \implies x - 4 \gt 0 \)) Working backwards from the consequent, and trying to arrive at the antecedent, we get \[ \begin{array}{rcl} |
Find \( \delta \) corresponding to \( \epsilon \) for a proof that \(\displaystyle \lim_{x \to 1^−}\sqrt{1−x}=0\).
- Hint
-
Sketch the graph and use Example \(\PageIndex{6}\) as a solving guide.
- Answer
-
\( \delta = \epsilon ^2\)
Key Concepts
- The intuitive notion of a limit may be converted into a rigorous mathematical definition known as the epsilon-delta definition of the limit.
- The epsilon-delta definition may be used to prove statements about limits.
- The epsilon-delta definition of a limit may be modified to define one-sided limits.
- A similar definition of an infinite limit can be used to prove statements about infinite limits.
Glossary
- epsilon-delta definition of the limit
- \(\displaystyle \lim_{x \to a}f(x)=L\) if for every \( \epsilon >0\), there exists a \( \delta >0\) such that if \(0<|x−a|< \delta \), then \(|f(x)−L|< \epsilon \)
- triangle inequality
- If \(a\) and \(b\) are any real numbers, then \(|a+b| \leq |a|+|b|\)
- formal definition of an infinite limit
- \(\displaystyle \lim_{x \to a}f(x)=\infty\) if for every \(M>0\), there exists a \( \delta >0\) such that if \(0<|x−a|< \delta \), then \(f(x)>M\)
\(\displaystyle \lim_{x \to a}f(x)=-\infty\) if for every \(M>0\), there exists a \( \delta >0\) such that if \(0<|x−a|< \delta \), then \(f(x)<-M\)


