3.6: Differentiation Techniques - Implicit Differentiation

Learning Objectives

• Use implicit differentiation to find the derivative given an implicitly-defined relation between two variables.
• Use implicit differentiation to determine the equation of a tangent line to an implicitly-defined curve.

We have already studied how to find equations of tangent lines to functions and the rate of change of a function at a specific point. In all these cases we had the explicit equation for the function and differentiated these functions explicitly. Suppose instead that we want to determine the equation of a tangent line to an arbitrary curve or the rate of change of an arbitrary curve at a point. In this section, we solve these problems by finding the derivatives of functions that define \(y\) implicitly in terms of \(x\).

Implicit Differentiation

In most discussions of math, if the dependent variable \(y\) is a function of the independent variable \(x\), we express \(y\) in terms of \(x\). If this is the case, we say that \(y\) is an explicit function of \(x\). For example, when we write the equation \(y=x^2+1\), we are defining \(y\) explicitly in terms of \(x\). On the other hand, if the relationship between the function \(y\) and the variable \(x\) is expressed by an equation where \(y\) is not expressed entirely in terms of \(x\), we say that the equation defines \(y\) implicitly in terms of \(x\). For example, the equation \(y−x^2=1\) defines the function \(y=x^2+1\) implicitly.

Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the Vertical Line Test). We are using the idea that portions of \(y\) are functions that satisfy the given equation, but that \(y\) is not actually a function of \(x\).

In general, an equation defines a function implicitly if the function satisfies that equation. An equation may define many different functions implicitly. For example, the functions

\[y=\sqrt{25−x^2}\nonumber \]

and

\[y=\begin{cases}\sqrt{25−x^2}, & \text{if }−5 \leq x<0\\ −\sqrt{25−x^2}, & \text{if }0 \leq x \leq 5\end{cases}\nonumber \]

which are illustrated in Figure \(\PageIndex{1}\), are just two of the many functions defined implicitly by the equation \(x^2+y^2=25\).

Figure \(\PageIndex{1}\):The equation \(x^2+y^2=25\) defines many functions implicitly.

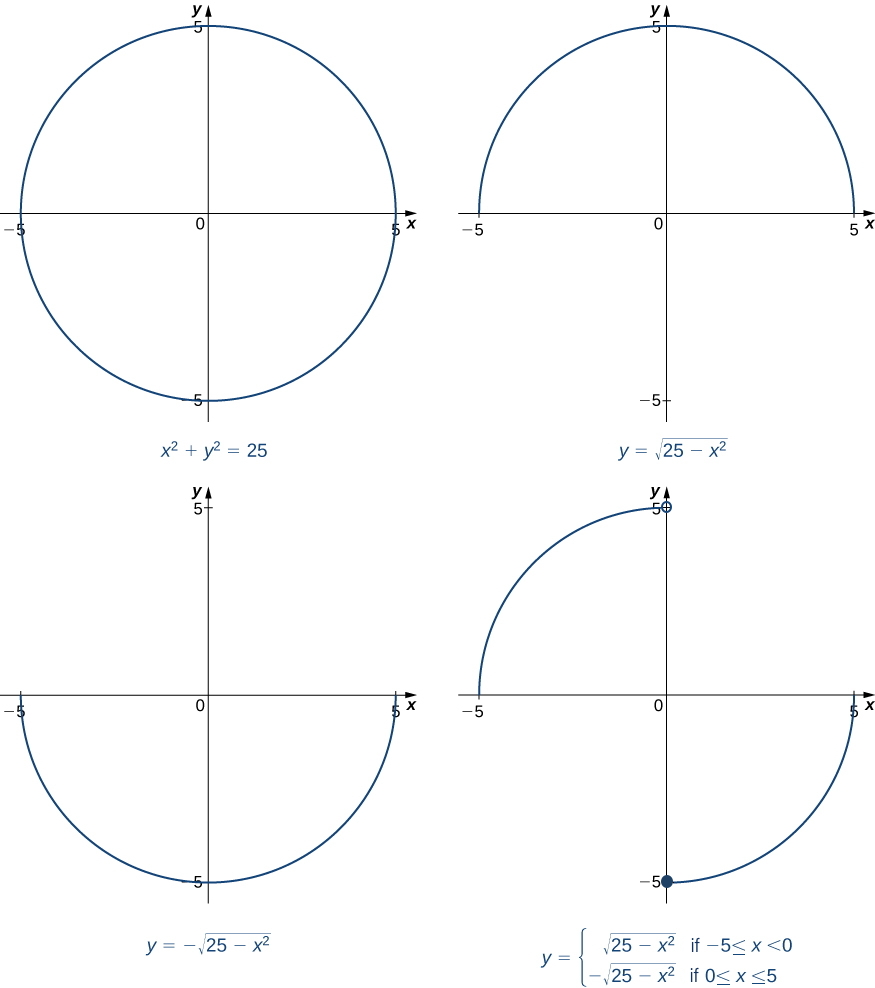
If we want to find the slope of the line tangent to the graph of \(x^2+y^2=25\) at the point \((3,4)\), we could evaluate the derivative of the function \(y=\sqrt{25−x^2}\) at \(x=3\). On the other hand, if we want the slope of the tangent line at the point \((3,−4)\), we could use the derivative of \(y=−\sqrt{25−x^2}\). However, it is not always easy to solve for a function defined implicitly by an equation. Fortunately, the technique of implicit differentiation allows us to find the derivative of an implicitly-defined function without ever solving for the function explicitly.

A simplified explanation of implicit differentiation is that you take the derivatives of both sides of a given equation (whether explicitly solved for \(y\) or not) with respect to the independent variable and perform the Chain Rule whether or not it is necessary. For example, suppose \(y = \sinh{(x)} - 2^x\). Then

\[ \begin{array}{rcl}
\dfrac{d}{dx} \left( y \right) = \dfrac{d}{dx} \left( \sinh{(x)} - 2^x \right) & \implies & \dfrac{dy}{dx} = \cosh{(x)} \dfrac{dx}{dx} - 2^x \ln{(2)} \dfrac{dx}{dx} \\
& \implies & \dfrac{dy}{dx} = \cosh{(x)} \cdot 1 - 2^x \ln{(x)} \cdot 1 \\
& \implies & \dfrac{dy}{dx} = \cosh{(x)} - 2^x \ln{(x)} \\
\end{array} \nonumber \]

While the results are no different than how we have performed differentiation so far, the process is important to understand. Suppose, instead, that we had the equation \(\cos{(x^2+x)} = \tanh{(x)} + 3y\) and were asked to find \(y^{\prime}\). We could start by solving for \(y\), or we could just take the derivative of both sides immediately as follows:

\[ \begin{array}{rcl}
\dfrac{d}{dx} \left( \cos{(x^2+x)} \right) = \dfrac{d}{dx} \left( \tanh{(x)} + 3y \right) & \implies & -\sin{(x^2 +x)} \cdot \dfrac{d}{dx} \left( x^2 + x\right) = \text{sech}^2(x) \dfrac{dx}{dx} + 3 \dfrac{dy}{dx} \\
& \implies & -\sin{(x^2 +x)} \cdot \left( 2x + 1\right) \cdot \dfrac{dx}{dx} = \text{sech}^2(x) \cdot 1 + 3 \dfrac{dy}{dx} \\
& \implies & -\sin{(x^2 +x)} \cdot \left( 2x + 1\right) \cdot 1 = \text{sech}^2(x) \cdot 1 + 3 \dfrac{dy}{dx} \\
& \implies & \dfrac{-\sin{(x^2 +x)} \cdot \left( 2x + 1\right) - \text{sech}^2(x)}{3} = \dfrac{dy}{dx} \\
\end{array} \nonumber \]

However, the real power of implicit differentiation comes into play when given the equation for an implicitly-defined curve. For example, if \(e^{xy} - \sqrt{x + y} = \cot{(y)}\), then the derivative of \(y\) with respect to \(x\) can be found by taking the derivative implicitly.

\[ \begin{array}{rcl}
\dfrac{d}{dx} \left( e^{xy} - \sqrt{x + y} \right) = \dfrac{d}{dx} \left( \cot{(y)} \right) & \implies & \dfrac{d}{dx} e^{xy} - \dfrac{d}{dx}\sqrt{x + y} = -\csc^2{(y)} \cdot \dfrac{dy}{dx} \\
& \implies & e^{xy} \cdot \dfrac{d}{dx} \left( xy \right) - \dfrac{1}{2 \sqrt{x + y}} \cdot \dfrac{d}{dx} \left( x + y \right) = -\csc^2{(y)} \cdot \dfrac{dy}{dx} \\
& \implies & e^{xy} \cdot \left(\dfrac{dx}{dx} \cdot y + x \cdot \dfrac{dy}{dx} \right) - \dfrac{1}{2 \sqrt{x + y}} \cdot \left( \dfrac{dx}{dx} + \dfrac{dy}{dx} \right) = -\csc^2{(y)} \cdot \dfrac{dy}{dx} \\
& \implies & e^{xy} \cdot \left(y + x \cdot \dfrac{dy}{dx} \right) - \dfrac{1}{2 \sqrt{x + y}} \cdot \left( 1 + \dfrac{dy}{dx} \right) = -\csc^2{(y)} \cdot \dfrac{dy}{dx} \\
\end{array} \nonumber \]

At this point, we would feel compelled to solve for \(\frac{dy}{dx}\); however, let's hold off for now. It's enough at this point to understand how implicit differentiation works.

Example \(\PageIndex{1}\): Using Implicit Differentiation

Assuming that \(y\) is defined implicitly by the equation \(x^2+y^2=25\), find \(\dfrac{dy}{dx}\).

Solution

\[ \begin{array}{rrclr}
& \dfrac{d}{dx}(x^2+y^2) & = & \dfrac{d}{dx}(25) & \left( \text{Differentiate both sides of the equation.} \right) \\
\implies & \dfrac{d}{dx}(x^2)+\dfrac{d}{dx}(y^2) & = & 0 & \left( \text{Use the Sum Rule on the left. On the right }\dfrac{d}{dx}(25)=0. \right) \\
\implies & 2x+2y\dfrac{dy}{dx} & = & 0 & \left( \text{Take the derivatives, so }\dfrac{d}{dx}(x^2)=2x\text{ and }\dfrac{d}{dx}(y^2)=2y\dfrac{dy}{dx}. \right) \\
\implies & 2y\dfrac{dy}{dx} & = & −2x & \left( \text{Keep the terms with }\dfrac{dy}{dx}\text{ on the left. Move the remaining terms to the right.} \right) \\
\implies & \dfrac{dy}{dx} & = & −\dfrac{x}{y} & \left( \text{Divide both sides of the equation by }2y. \right) \\
\end{array} \nonumber \]

Analysis

Note that the resulting expression for \(\frac{dy}{dx}\) is in terms of both the independent variable \(x\) and the dependent variable \(y\). Although in some cases it may be possible to express \(\frac{dy}{dx}\) in terms of \(x\) only, it is generally not possible to do so.

Example \(\PageIndex{2}\): Using Implicit Differentiation and the Product Rule

Assuming that \(y\) is defined implicitly by the equation \(x^3\sin y+y=4x+3\), find \(\frac{dy}{dx}\).

Solution

\[ \begin{array}{rrclr}
& \dfrac{d}{dx}(x^3\sin y+y) & = & \dfrac{d}{dx}(4x+3) & \left( \text{Differentiate both sides of the equation.} \right) \\
\implies & \dfrac{d}{dx}(x^3\sin y)+\dfrac{d}{dx}(y) & = & 4 & \left( \text{Apply the Sum Rule on the left. On the right, }\dfrac{d}{dx}(4x+3)=4 \right) \\
\implies & \left(\dfrac{d}{dx}(x^3) \cdot \sin y+\dfrac{d}{dx}(\sin y) \cdot x^3\right)+\dfrac{dy}{dx} & = & 4 & \left( \text{Use the Product Rule to find }\dfrac{d}{dx}(x^3\sin y)\text{. Observe that }\dfrac{d}{dx}(y)=\dfrac{dy}{dx}. \right) \\
\implies & 3x^2\sin y+(\cos y\dfrac{dy}{dx}) \cdot x^3+\dfrac{dy}{dx} & = & 4 & \left( \text{We know }\dfrac{d}{dx}(x^3)=3x^2\text{. Use the Chain Rule to obtain }\dfrac{d}{dx}(\sin y)=\cos y\dfrac{dy}{dx}. \right) \\
\implies & x^3\cos y\dfrac{dy}{dx}+\dfrac{dy}{dx} & = & 4−3x^2\sin y & \left( \text{Keep all terms containing }\dfrac{dy}{dx}\text{ on the left. Move all other terms to the right.} \right) \\
\implies & \dfrac{dy}{dx}(x^3\cos y+1) & = & 4−3x^2\sin y & \left( \text{Factor out }\dfrac{dy}{dx}\text{ on the left.} \right) \\
\implies & \dfrac{dy}{dx} & = & \dfrac{4−3x^2\sin y}{x^3\cos y+1} & \left( \text{Solve for }\dfrac{dy}{dx}\text{ by dividing both sides of the equation by }x^3\cos y+1. \right) \\
\end{array} \nonumber \]

Example \(\PageIndex{3}\): Using Implicit Differentiation to Find a Second Derivative

Find \(\frac{d^2y}{dx^2}\) if \(x^2+y^2=25\).

Solution

In Example \(\PageIndex{1}\), we showed that \(\frac{dy}{dx}=−\frac{x}{y}\). We can take the derivative of both sides of this equation to find \(\frac{d^2y}{dx^2}\).

\[\begin{array}{rclr}
\dfrac{d^2y}{dx^2} & = & \dfrac{d}{dy}\left(−\dfrac{x}{y}\right) & \left( \text{Differentiate both sides of }\dfrac{dy}{dx}=−\dfrac{x}{y}. \right)\\
& = & −\dfrac{\left(1 \cdot y−x\dfrac{dy}{dx}\right)}{y^2} & \left( \text{Use the Quotient Rule to find }\dfrac{d}{dy}\left(−\dfrac{x}{y}\right). \right) \\
& = & \dfrac{−y+x\dfrac{dy}{dx}}{y^2} & \\
& = & \dfrac{−y+x\left(−\dfrac{x}{y}\right)}{y^2} & \left( \text{Substitute }\dfrac{dy}{dx}=−\dfrac{x}{y}. \right) \\
& = & \dfrac{−y^2−x^2}{y^3} & \\
\end{array}\nonumber\]

At this point we have found an expression for \(\frac{d^2y}{dx^2}\). If we choose, we can simplify the expression further by recalling that \(x^2+y^2=25\) and making this substitution in the numerator to obtain \(\frac{d^2y}{dx^2}=−\frac{25}{y^3}\).

Exercise \(\PageIndex{3}\)

Find \(\frac{dy}{dx}\) for \(y\) defined implicitly by the equation \(4x^5+\tan y=y^2+5x\).

Hint

Remember to apply the Chain Rule to differentiate \(\tan y\) and \(y^2\).

Answer

\[\dfrac{dy}{dx}=\dfrac{5−20x^4}{\sec^2y−2y} \nonumber \]

Finding Tangent Lines Implicitly

Now that we have seen the technique of implicit differentiation, we can apply it to the problem of finding equations of tangent lines to curves described by equations.

Note

When asked to find the value of the derivative or the equation of the tangent line for an implicitly-defined curve at a given point, it's best to not solve for \( \frac{dy}{dx} \) immediately after implicitly differentiating. Instead, once you have implicitly differentiated the relation, substitute the given values of \( x \) and \( y \) into the resulting equation. It is at that point that you should solve for \( \frac{dy}{dx} \). Examples \( \PageIndex{4} \) and \( \PageIndex{5}  \) illustrate this process.

Example \(\PageIndex{4}\): Finding the Equation of a Tangent Line

Find the equation of the line tangent to the curve \(\cosh{(xy)} + xy = \frac{5}{4} + \ln{(2)}\) at the point \((1,\ln{(2)})\).

Solution

\[ \begin{array}{rrclr}
& \dfrac{d}{dx}\left( \cosh{(xy)} + xy \right) & = & \dfrac{d}{dx}\left( \dfrac{5}{4} + \ln{(2)} \right) & \\
\implies & \dfrac{d}{dx}\cosh{(xy)} + \dfrac{d}{dx} \left( xy \right) & = & 0 & \left( \text{Sum Rule and Constant Rule} \right) \\
\implies & \sinh{(xy)} \cdot \dfrac{d}{dx}\left(xy\right) + \dfrac{d}{dx} \left( xy \right) & = & 0 & \left( \text{Chain Rule} \right) \\
\implies & \sinh{(xy)} \cdot \left( \dfrac{d}{dx}x \cdot y + x \cdot \dfrac{d}{dx} y \right) + \left( \dfrac{d}{dx}x \cdot y + x \cdot \dfrac{d}{dx} y \right) & = & 0 & \left( \text{Product Rule} \right) \\
\implies & \sinh{(xy)} \cdot \left( y + x \cdot \dfrac{dy}{dx} \right) + \left( y + x \cdot \dfrac{dy}{dx} \right) & = & 0 & \left( \text{Power Rule} \right) \\
\end{array} \nonumber \]

At this point, it is important to remember the task at hand. We are asked to find the equation of the tangent line to the curve \(\cosh{(xy)} + xy = \frac{5}{4} + \ln{(2)}\) at the point \((1,\ln{(2)})\). There is no need to explicitly solve for \( \frac{dy}{dx} \) at this moment. Instead, let's substitute \( 1 \) for \( x \) and \( \ln{(2)} \) for \( y \).

\[ \begin{array}{rrclr} 
 & \sinh{(\ln{(2)})} \cdot \left( \ln{(2)} + \dfrac{dy}{dx} \right) + \left( \ln{(2)} + \dfrac{dy}{dx} \right) & = & 0 & \left( \text{Substitution} \right) \\
\implies & \left( \sinh{(\ln{(2)})} + 1 \right) \cdot \left( \ln{(2)} + \dfrac{dy}{dx} \right) & = & 0 & \\
\implies & \left( \ln{(2)} + \dfrac{dy}{dx} \right) & = & 0 & \left( \text{Algebra: Dividing both sides by a nonzero constant}^* \right) \\
\implies & \dfrac{dy}{dx}\Big|_{(1, \ln{(2)})} & = & -\ln{(2)} & \\
\end{array} \nonumber \]

Now that we have the slope of the tangent line at the point \( (1, \ln{(2)} \), we use the point-slope form of a line to get the equation of the tangent line.

\[ y - \ln{(2)} = -\ln{(2)}(x - 1) \implies y = -\ln{(2)}x + 2 \ln{(2)}. \nonumber \]

Figure \( \PageIndex{2} \) shows the curve and the tangent line.

Figure \( \PageIndex{2} \)

^* I leave it to the reader to check that \( \sinh{(\ln{(2)})} + 1 \neq 0 \).

Example \(\PageIndex{5}\): Finding the Equation of the Tangent Line to a Curve

Find the equation of the line tangent to the graph of \(y^3+x^3−3xy=0\) at the point \(\left(\frac{3}{2},\frac{3}{2}\right)\) (Figure \(\PageIndex{3}\)). This curve is known as the folium (or leaf) of Descartes.

Figure \(\PageIndex{3}\): Finding the tangent line to the folium of Descartes at \(\left(\frac{3}{2},\frac{3}{2}\right)\).

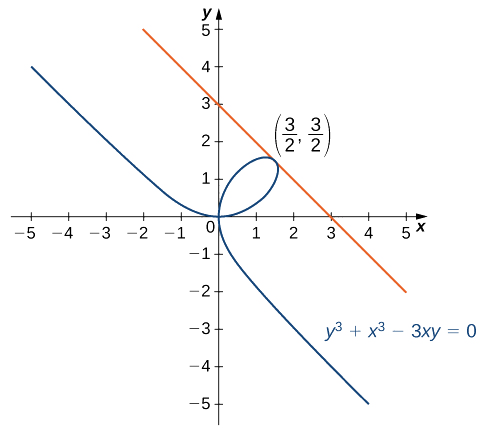
Solution

Begin by implicitly differentiating both sides.

\[ \begin{array}{rrcl}
& \dfrac{d}{dx}\big(y^3+x^3−3xy\big) & = & \dfrac{d}{dx}\big(0\big) \\
\implies & 3y^2\dfrac{dy}{dx}+3x^2−\left(3y+3x\dfrac{dy}{dx}\right) & = & 0 \\
\implies & 3y^2\dfrac{dy}{dx}+3x^2−3y-3x\dfrac{dy}{dx} & = & 0 \\
\end{array} \nonumber \]

At this point, it is important to read what we are being asked to do. We are not being asked to solve for \(dy/dx\), but instead to find the equation of the tangent line at \(\left(\frac{3}{2},\frac{3}{2}\right)\). As such, we let \(x = \frac{3}{2}\) and \(y = \frac{3}{2}\) in our implicitly-differentiated equation.

\[ \begin{array}{rrcl}
& 3 \left( \frac{3}{2} \right)^2 \dfrac{dy}{dx}+3 \left( \frac{3}{2} \right)^2−3 \left( \frac{3}{2} \right) -3 \left( \frac{3}{2} \right) \dfrac{dy}{dx} & = & 0 \\
\implies & \frac{27}{4} \dfrac{dy}{dx} + \frac{27}{4} − \frac{9}{2} - \frac{9}{2} \dfrac{dy}{dx} & = & 0 \\
\implies & 27 \dfrac{dy}{dx} + 27 − 18 - 18 \dfrac{dy}{dx} & = & 0 \\
\implies & 9 \dfrac{dy}{dx} + 9 & = & 0 \\
\implies & \dfrac{dy}{dx} & = & -1 \\
\end{array} \nonumber \]

Finally, substitute into the point-slope equation of the line to obtain

\(y=−x+3\).

Example \(\PageIndex{6}\): Applying Implicit Differentiation

In a simple video game, a rocket travels in an elliptical orbit whose path is described by the equation \(4x^2+25y^2=100\). The rocket can fire missiles along lines tangent to its path. The object of the game is to destroy an incoming asteroid traveling along the positive \(x\)-axis toward \((0,0)\). If the rocket fires a missile when it is located at \(\left(3,\frac{8}{5}\right)\), where will it intersect the \(x\)-axis?

Solution

To solve this problem, we must determine where the line tangent to the graph of \(4x^2+25y^2=100\) at \(\left(3,\frac{8}{5}\right)\) intersects the \(x\)-axis. Begin by finding \(\frac{dy}{dx}\) implicitly. Differentiating, we have

\[8x+50y\dfrac{dy}{dx}=0.\nonumber\]

Letting \(x = 3\) and \(y = \frac{8}{5}\), we get

\[ 8(3) + 50\left(\frac{8}{5}\right) \dfrac{dy}{dx} = 0 \implies 24 + 80 \dfrac{dy}{dx} = 0 \implies \dfrac{dy}{dx} = -\dfrac{3}{10}. \nonumber \]

The equation of the tangent line is \(y=−\frac{3}{10}x+\frac{5}{2}\). To determine where the line intersects the \(x\)-axis, solve \(0=−\frac{3}{10}x+\frac{5}{2}\). The solution is \(x=\frac{25}{3}\). The missile intersects the \(x\)-axis at the point \(\left(\frac{25}{3},0\right)\).

Exercise \(\PageIndex{6}\)

Find the equation of the line tangent to the hyperbola \(x^2−y^2=16\) at the point \((5,3)\).

Hint

\(\frac{dy}{dx}=\frac{x}{y}\)

Answer

\(y=\frac{5}{3}x−\frac{16}{3}\)

Key Concepts

• We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations).
• By using implicit differentiation, we can find the equation of a tangent line to the graph of a curve.

Glossary

implicit differentiation

is a technique for computing \(\dfrac{dy}{dx}\) for a function defined by an equation, accomplished by differentiating both sides of the equation (remembering to treat the variable \(y\) as a function) and solving for \(\dfrac{dy}{dx}\)