5.4E: Exercises

In exercises 1 - 12, use the Fundamental Theorem of Calculus, Part 1, to find each derivative.

1) \(\displaystyle \frac{d}{dx}\left[∫^x_1e^{−t^2}\,dt \right] \)

2) \(\displaystyle \frac{d}{dx}\left[∫^x_1e^{cost}\,dt \right] \)

Answer

\(\displaystyle \frac{d}{dx}\left[∫^x_1e^{cost}\,dt \right] = e^{\cos t}\)

3) \(\displaystyle \frac{d}{dx}\left[∫^x_3\sqrt{9−y^2}\,dy \right] \)

4) \(\displaystyle \frac{d}{dx}\left[∫^x_3\frac{ds}{\sqrt{16−s^2}} \right] \)

Answer

\(\displaystyle \frac{d}{dx}\left[∫^x_3\frac{ds}{\sqrt{16−s^2}} \right] = \frac{1}{\sqrt{16−x^2}}\)

5) \(\displaystyle \frac{d}{dx}\left[∫^{2x}x_t\,dt \right] \)

6) \(\displaystyle \frac{d}{dx}\left[∫^{\sqrt{x}}_0t\,dt \right] \)

Answer

\(\displaystyle \frac{d}{dx}\left[∫^{\sqrt{x}}_0t\,dt \right] = \sqrt{x}\frac{d}{dx}\big(\sqrt{x}\big)=\frac{1}{2}\)

7) \(\displaystyle \frac{d}{dx}\left[∫^{\sin x}_0\sqrt{1−t^2}\,dt \right] \)

8) \(\displaystyle \frac{d}{dx}\left[∫^1_{\cos x}\sqrt{1−t^2}\,dt \right] \)

Answer

\(\displaystyle \frac{d}{dx}\left[∫^1_{\cos x}\sqrt{1−t^2}\,dt \right] = −\sqrt{1−\cos^2x}\frac{d}{dx}\big(\cos x\big)=|\sin x|\sin x\)

9) \(\displaystyle \frac{d}{dx}\left[∫^{\sqrt{x}}_1\frac{t^2}{1+t^4}\,dt \right] \)

10) \(\displaystyle \frac{d}{dx}\left[∫^{x^2}_1\frac{\sqrt{t}}{1+t}\,dt \right] \)

Answer

\(\displaystyle \frac{d}{dx}\left[∫^{x^2}_1\frac{\sqrt{t}}{1+t}\,dt \right] = 2x\dfrac{|x|}{1+x^2}\)

11) \(\displaystyle \frac{d}{dx}\left[∫^{\ln x}_0e^t\,dt \right] \)

12) \(\displaystyle \frac{d}{dx}\left[∫^{e^{x}}_1\ln u^2\,du \right] \)

Answer

\(\displaystyle \frac{d}{dx} \left[ ∫^{e^{x}}_1\ln u^2\,du \right] = \ln(e^{2x})\dfrac{d}{dx}\big(e^x\big)=2xe^x\)

13) The graph of \(\displaystyle y=∫^x_0f(t)\,dt\), where \(f\) is a piecewise constant function, is shown here.

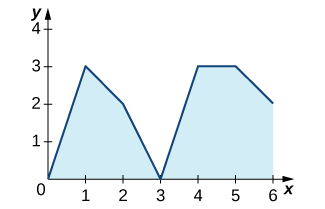
a. Over which intervals is \(f\) positive? Over which intervals is it negative? Over which intervals, if any, is it equal to zero?

b. What are the maximum and minimum values of \(f\)?

14) The graph of \(\displaystyle y=∫^x_0f(t)\,dt\), where \(f\) is a piecewise constant function, is shown here.

a. Over which intervals is \(f\) positive? Over which intervals is it negative? Over which intervals, if any, is it equal to zero?

b. What are the maximum and minimum values of \(f\)?

Answer

a. \(f\) is positive over \([1,2]\) and \([5,6]\), negative over \( [0,1]\) and \([3,4]\), and zero over \([2,3]\) and \([4,5]\).
b. The maximum value is \(2\) and the minimum is \(−3\).

15) The graph of \(\displaystyle y=∫^x_0ℓ(t)\,dt\), where \(ℓ\) is a piecewise linear function, is shown here.

a. Over which intervals is \(ℓ\) positive? Over which intervals is it negative? Over which, if any, is it zero?

b. Over which intervals is \(ℓ\) increasing? Over which is it decreasing? Over which, if any, is it constant?

16) The graph of \(\displaystyle y=∫^x_0ℓ(t)\,dt\), where \( ℓ\) is a piecewise linear function, is shown here.

a. Over which intervals is \(ℓ\) positive? Over which intervals is it negative? Over which, if any, is it zero?

b. Over which intervals is \(ℓ\) increasing? Over which is it decreasing? Over which intervals, if any, is it constant?

Answer

a. \(ℓ\) is positive over \([0,1]\) and \([3,6]\), and negative over \([1,3]\).
b. It is increasing over \([0,1]\) and \([3,5]\), and it is constant over \([1,3]\) and \([5,6]\).

In exercises 17 - 36, evaluate each definite integral using the Fundamental Theorem of Calculus, Part 2.

17) \(\displaystyle ∫^2_{−1}(x^2−3x)\,dx\)

18) \(\displaystyle ∫^3_{−2}(x^2+3x−5)\,dx\)

Answer

\(\displaystyle F(x)=\frac{x^3}{3}+\frac{3x^2}{2}−5x,\quad F(3)−F(−2)=−\frac{35}{6}\)

19) \(\displaystyle ∫^3_{−2}(t+2)(t−3)dt\)

20) \(\displaystyle ∫^3_2(t^2−9)(4−t^2)dt\)

Answer

\(F(x)=−\dfrac{t^5}{5}+\dfrac{13t^3}{3}−36t,\quad F(3)−F(2)=\frac{62}{15}\)

21) \(\displaystyle ∫^2_1x^9\,dx\)

22) \(\displaystyle ∫^1_0x^{99}\,dx\)

Answer

\(F(x)=\dfrac{x^{100}}{100},\quad F(1)−F(0)=\dfrac{1}{100}\)

23) \(\displaystyle ∫^8_4(4t^{5/2}−3t^{3/2})dt\)

24) \(\displaystyle ∫^4_{1/4}\left(x^2−\dfrac{1}{x^2}\right)\,dx\)

Answer

\(F(x)=\dfrac{x^3}{3}+\dfrac{1}{x},\quad F(4)−F\left(\tfrac{1}{4}\right)=\frac{1125}{64}\)

25) \(\displaystyle ∫^2_1\frac{2}{x^3}\,dx\)

26) \(\displaystyle ∫^4_1\frac{1}{2\sqrt{x}}\,dx\)

Answer

\(F(x)=\sqrt{x},\quad F(4)−F(1)=1\)

27) \(\displaystyle ∫^4_1\frac{2−\sqrt{t}}{t^2}\,dt\)

28) \(\displaystyle ∫^{16}_1\frac{dt}{t^{1/4}}\)

Answer

\( F(t)=\frac{4}{3}t^{3/4},\quad F(16)−F(1)=\frac{28}{3}\)

29) \(\displaystyle ∫^{2π}_0\cos θ\,dθ\)

30) \(\displaystyle ∫^{π/2}_0\sin θ\,dθ\)

Answer

\(F(θ)=−\cos θ,\quad F(\frac{π}{2})−F(0)=1\)

31) \(\displaystyle ∫^{π/4}_0\sec^2 θ\,dθ\)

32) \(\displaystyle ∫^{π/4}_0\sec θ\tan θ\,dθ\)

Answer

\(F(θ)=\sec θ,\quad F(\frac{π}{4})−F(0)=\sqrt{2}−1\)

33) \(\displaystyle ∫^{π/4}_{π/3}\csc θ\cot θ\,dθ\)

34) \(\displaystyle ∫^{π/2}_{π/4}\csc^2 θ\,dθ\)

Answer

\(F(θ)=−\cot θ,\quad F(\frac{π}{2})−F(\frac{π}{4})=1\)

35) \(\displaystyle ∫^2_1\left(\frac{1}{t^2}−\frac{1}{t^3}\right)\,dt\)

36) \(\displaystyle ∫^{−1}_{−2}\left(\frac{1}{t^2}−\frac{1}{t^3}\right)\,dt\)

Answer

\( F(t)=−\dfrac{1}{t}+\dfrac{1}{2t^2},\quad F(−1)−F(−2)=\frac{7}{8}\)

In exercises 37 - 40, use the evaluation theorem to express the integral as a function \(F(x).\)

37) \(\displaystyle ∫^x_at^2\,dt\)

38) \(\displaystyle ∫^x_1e^t\,dt\)

Answer

\(F(x)=e^x−e\)

39) \(\displaystyle ∫^x_0\cos t\,dt\)

40) \(\displaystyle ∫^x_{−x}\sin t\,dt\)

Answer

\(F(x)=0\)

In exercises 41 - 44, identify the roots of the integrand to remove absolute values, then evaluate using the Fundamental Theorem of Calculus, Part 2.

41) \(\displaystyle ∫^3_{−2}|x|\,dx\)

42) \(\displaystyle ∫^4_{−2}∣t^2−2t−3∣\,dt\)

Answer

\(\displaystyle ∫^{−1}_{−2}(t^2−2t−3)\,dt−∫^3_{−1}(t^2−2t−3)\,dt+∫^4_3(t^2−2t−3)\,dt=\frac{46}{3}\)

43) \(\displaystyle ∫^π_0|\cos t|\,dt\)

44) \(\displaystyle ∫^{π/2}_{−π/2}|\sin t|\,dt\)

Answer

\(\displaystyle −∫^0_{−π/2}\sin t\,dt+∫^{π/2}_0\sin t\,dt=2\)